Makeloft Webサイトの記事の最新版多くの人にとって
、損失のあるオーディオ圧縮は魔法のブラックボックスに似ていると思います。人間の耳にはほとんど見えない、または聞こえない冗長な情報が失われるため、数学的な錬金術を使用して驚くほど複雑な方法でデータが圧縮され、その結果、録音品質がいくらか低下します。 しかし、そのような損失の重要性を即座に評価し、その本質を理解することは非常に簡単ではありません。 しかし、今日はそこに何が問題なのかを見つけようとし、そのおかげで
何十回も同じようなデータ圧縮プロセスが一般的に可能です...
カーテンを取り外し、ドアを開け、心と心を刺激する神秘的なアルゴリズムを個人的に見てみましょう。
露出のセッションへようこそ！
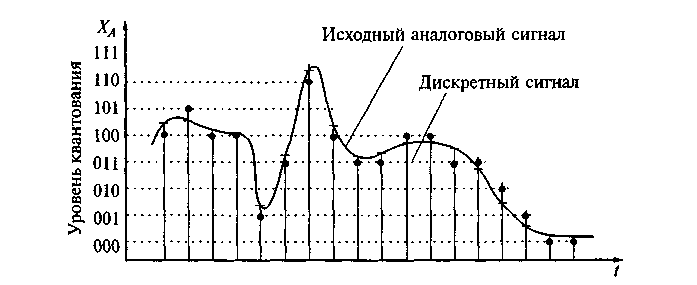
非圧縮オーディオストリームは、たとえば、マイクバッファーからの整数の配列（
C＃short ）です。 これは、一定の間隔（つまり、特定のサンプリングレートとレベルごとの量子化）で取得されたアナログ信号の振幅値の離散セットです。
*簡単にするために、以下では古典的なモノラル信号を検討しますこの配列をすぐにファイルに書き込むと、短い時間間隔でも非常に膨大になります。 明らかに、そのようなストリーム信号には多くの冗長データが含まれているため
、正しいデータ
を選択して冗長データ
を削除するにはどうすればよいかという疑問が自然に発生
します。 それに対する答えは、単純で厳しく
、フーリエ変換を使用します。
はい、それは技術大学で定期的に解釈され、忘れることができたものです。 ただし、これは重要ではありません-
紹介プレゼンテーションを研究し 、問題が詳細に検討されて
いる記事を
読みます。
C＃で
32行のコードを測定するだけのアルゴリズム自体が必要です。
public static Complex[] DecimationInTime(this Complex[] frame, bool direct) { if (frame.Length == 1) return frame; var frameHalfSize = frame.Length >> 1;
変換は信号の小さな部分に適用されます。サンプル数は2のべき乗の倍数で、通常は
1024、2048、4096です。
Kotelnikov-Nyquist-Shannonの定理によれば、標準のサンプリング周波数
44100 Hzで 、歪みのない
22050 Hzまでのスペクトルの最大周波数の元の信号を復元することができます。それぞれ
93ミリ秒 。 次に、この信号フラグメントの位相スペクトルと周波数スペクトルに関する情報を含む複素数の配列（フレームと同じ長さ）を取得します。 結果の配列は、コピーの2つのミラー部分で構成されているため、その要素の半分だけが実際の情報コンテンツを持っています。
この段階では、
静かな周波数に関する情報を削除し 、例えば辞書の形で
大きな音のみを保存し、再生中に失われた要素をゼロに置き換えて復元し、逆フーリエ変換を実行して再生に適した信号を取得します。
この原理に基づいて、膨大な数のオーディオコーデックの処理が行われます。これは、説明した操作により数十回または数百回（！）の圧縮が可能になるためです。 もちろん、情報をファイルに書き込む方法も結果のサイズを調整し、追加にはほど遠いロスレスアーカイブアルゴリズムの追加使用になりますが、
最も重要な貢献は、聞こえない周波数の消音によって提供されます 。
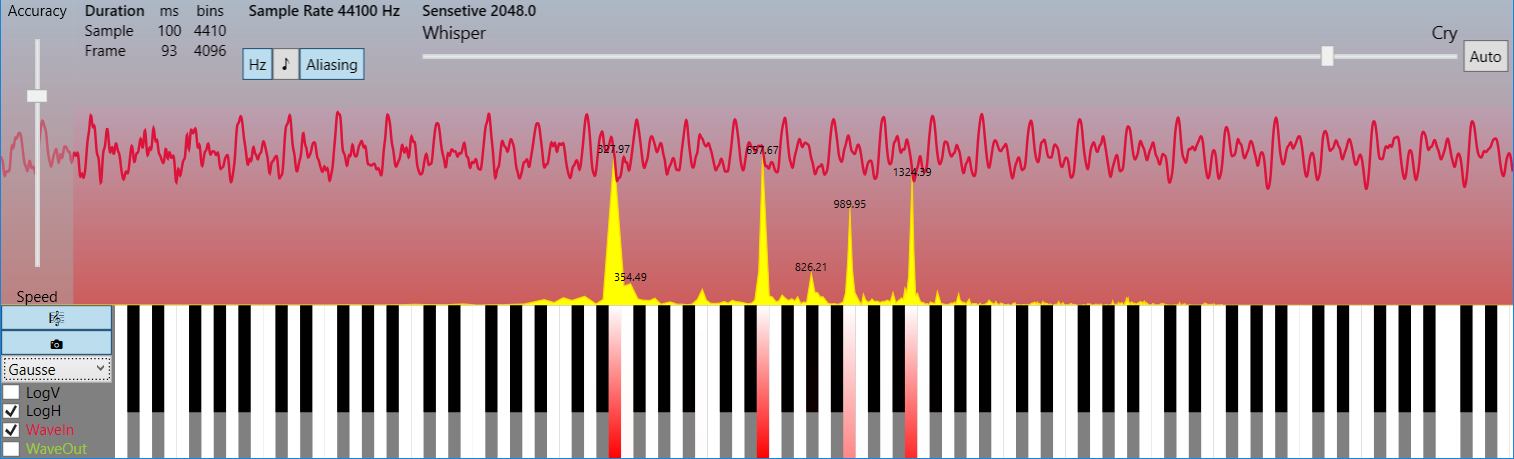
最初は、このような重要な圧縮率がそれほど簡単な方法で達成できるとは信じられませんが、対数目盛ではなく線形周波数目盛でスペクトル画像を見ると、実際のスペクトルでは有用な情報を伝える狭い高調波のセットしか通常ないことがすぐに明らかになります、そして、他のすべては聴覚を超えたわずかなノイズです。
そして、逆説的に見えるかもしれませんが、低い圧縮率では、信号は知覚のために劣化しませんが、逆にノイズを取り除くだけです、つまり理想化されています！
*写真は、4096サンプル（93ミリ秒）のフレームと22050 Hzまでの周波数スペクトルを示しています（ソースコードのLimitFrequencyを参照）。 この例は、実際の信号のキャリア高調波が少ないことを示しています。根拠にならないように、
デモアプリケーション（ Rainbow Framework ）をテストすることを提案します。この場合、圧縮アルゴリズムはごく単純ですが、非常に機能的です。 同時に、圧縮の程度に応じて発生する歪みを評価したり、音などを視覚化する方法を学習したりできます...
var fftComplexFrequencyFrame = inputComplexTimeFrame.DecimationInTime(true); var y = 0; var original = fftComplexFrequencyFrame.ToDictionary(c => y++, c => c); var compressed = original.OrderByDescending(p => p.Value.Magnitude).Take(CompressedFrameSize).ToList();
はい、もちろん、知覚の心理音響モデル、特定の周波数がスペクトルに現れる可能性などを考慮に入れた不可解なアルゴリズムがありますが、それらはすべて、適切な品質を維持しながらパフォーマンスを部分的に改善するのに役立ちますが、圧縮の大部分はこのような簡単な方法で達成されますC＃で文字通り数行しかかからないように。
したがって、一般的な圧縮スキームは次のとおりです。
1.信号の振幅時間フレームへの分割*
2.直接フーリエ変換-振幅周波数フレームの取得
3.静かな周波数の完全な消音と追加のオプションの処理
4.ファイルへのデータの書き込み
*多くの場合、フレームは互いに部分的にオーバーラップします。これにより、特定の高調波の信号が1つのフレームで開始または終了するときのクリックを回避できますが、別のフレームでは音が完全に強まり、消音されませんが、依然として弱く消音されます。 このため、正弦波の位相に応じて、重なり合わないフレームの境界で振幅が急激にジャンプする可能性があり、クリックとして認識されます。逆のプロセスには、次の手順が含まれます。
1.ファイルの読み取り
2.振幅周波数フレームの回復
3.逆フーリエ変換-振幅時間フレームの取得
4.振幅時間フレームからの信号の形成
以上です。 おそらくもっと複雑なものを期待していましたか？
参照：
1.
紹介プレゼンテーション2.
フーリエ変換の記事3.
ソースコードを使用したデモアプリケーション（Rainbow Framework）（
バックアップリンク ）