最近、バーンスタインによって提案された楕円曲線のバリエーションに基づく電子署名Ed25519は、ますます人気を集めています。 Ed25519は一般的な暗号ライブラリの一部ではないため、このタイプの署名を持つI2Pノードの数が増えるにつれて、I2Pの実装でそれをサポートすることが必要になりました。 原則として、さまざまなref10が
SUPERCOPライブラリから使用され、Bernstein自身がアセンブラーで実装し、他の言語に移植します。 この実装は迅速かつ適切に機能しますが、大きな欠点があります-わかりにくいです。 確かに、ソースコードを見ると、同じタイプの多数の行が多くの「マジック」番号で動作していることがわかりますが、理論を詳しく調べないと、それらの意味を理解することはできません。 この記事の目的は、Ed22519の数学的に透過的な実装です。I2Pでの実用に十分な作業速度で、暗号ライブラリに多数の標準操作のみを使用します。
楕円暗号の動作原理
楕円曲線と呼ばれる特殊な形の平面曲線の暗黙的な方程式が指定されています。 剰余体を法とする素数が指定されます。 曲線の点の座標は、このフィールドに属します。 モジュラスを超えない非負の整数です。 曲線の2つのポイントの上で、追加操作が指定されているため、新しいポイントも曲線に属します。 ポイントがそれ自体に追加された場合、再度追加すると2倍になり、次に3倍になるなど、任意の数nが乗算されます。 また、曲線とともに、曲線に属する基点が設定され、その操作は暗号化で使用されます。
暗号化では、任意の大きな数字nが選択されます。これは秘密キーであり、ベースポイントにそれが乗算され、新しいポイントは公開キーとして機能します。 永続性は、妥当な時間内のポイントから乗数を決定するための現在知られている方法の欠如に基づいています
Ed25519
Bershteinは、次のパラメーターで楕円曲線を使用することを提案しました。
曲線方程式: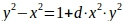
どこで
 モジュール:q
モジュール:q =

したがって、曲線の名前。
基点 :
(x、4/5)、xは方程式を解くことにより得られます(以下を参照)
明示的な形式の座標:
x = 15112221349535400772501151409588531511454012693041857206046113283949847762202、
y = 46316835694926478169428394003475163141307993866256225615783033603165251855960。
追加:
どこで

ここでの除算は、通常の剰余除算ではなく、式による
フェルマーの小定理に従って計算された逆モジュロ要素による乗算であることに注意してください

、つまりモジュロをべき乗する操作。
必要に応じて、
y座標のみを公開キーとして使用し、xに関する曲線の方程式を解き、次の式で計算することを提案します。

。
qは 8 * k + 5として表す
ことができるため、
xの平方根を計算するには、次の式を使用します。

。 確かにq =

=

、したがって平方根

。
実装
コードは、Signature.cppファイルの
アドレスに完全に配置され
ています。 多数を処理するために、opensslの
BNライブラリーの関数が使用されます。
曲線自体を実装し、そのコンストラクターで計算された曲線パラメーターを含むEd25519クラスを作成しましょう。 まず、3つの方法が必要です。加算、数値による乗算、および指定されたyに対するxの計算です。
class Ed25519 { //... EDDSAPoint Sum (const EDDSAPoint& p1, const EDDSAPoint& p2) const EDDSAPoint Mul (const EDDSAPoint& p, const BIGNUM * e) const BIGNUM * RecoverX (const BIGNUM * y) const //... }
私的使用、加算演算、除算演算の複雑さにより、xとyを共通分母(1 + m)*(1-m)に持って行き、それにより1つの除算を排除します。 その結果、追加するコードは次のようになります。
// m = d*p1.x*p2.x*p1.y*p2.y BN_mul (xx, p1.x, p2.x, m_Ctx); //p1.x*p2.x BN_mul (yy, p1.y, p2.y, m_Ctx); //p1.y*p2.y BIGNUM * m = BN_dup (d); BN_mul (m, m, xx, m_Ctx); BN_mul (m, m, yy, m_Ctx); // x = (p1.x*p2.y + p2.x*p1.y)*inv(1 + m) // y = (p1.y*p2.y + p1.x*p2.x)*inv(1 - m) // m1 = 1-m BN_one (m1); BN_sub (m1, m1, m); // m = m+1 BN_add_word (m, 1); // y = (p1.y*p2.y + p1.x*p2.x)*m BN_add (y, xx, yy); BN_mod_mul (y, y, m, q, m_Ctx); // x = (p1.x*p2.y + p2.x*p1.y)*m1 BN_mul (yy, p1.x, p2.y, m_Ctx); BN_mul (xx, p2.x, p1.y, m_Ctx); BN_add (x, xx, yy); // denominator m = m*m1 BN_mod_mul (m, m, m1, q, m_Ctx); Inv (m); BN_mod_mul (x, x, m, q, m_Ctx); // x = x/m BN_mod_mul (y, y, m, q, m_Ctx); // y = y/m
また、この場合はp1.x = p2.xおよびp1.y = p2.yであるため、乗算の数を減らすことができるため、二重化(ポイントをそれ自体で追加)するために、個別のDoubleメソッドが実装されます。 さらに、BN_mulの代わりに高速のBN_sqrが使用されます。
乗算は、
倍加と加算の最も単純な方法、つまり 各ステップで結果の値を2倍にし、ビットが1である場合、乗算されたポイントを追加します。
EDDSAPoint res {zero, one}; if (!BN_is_zero (e)) { int bitCount = BN_num_bits (e); for (int i = bitCount - 1; i >= 0; i--) { res = Double (res); if (BN_is_bit_set (e, i)) res = Sum (res, p); } }
xをyで計算するのは簡単です。
まず、ルート式:
BN_sqr (y2, y, m_Ctx); // y^2 // xx = (y^2 -1)*inv(d*y^2 +1) BN_mul (xx, d, y2, m_Ctx); BN_add_word (xx, 1); Inv (xx); BN_sub_word (y2, 1); BN_mul (xx, y2, xx, m_Ctx);
次に、式を使用して平方根を計算します

署名と署名検証
このトピックは非常に興味深く、広範囲にわたるため、この問題
については
別の記事で取り上げます。 同時に、SignメソッドとVerifyメソッドが実装され、実際に使用されています。 したがって、興味がある人は誰でもコードを調べることができます。 ここでは、一部の機能のみがリストされます。
他の電子署名システムと同様に、EdDSA署名は32バイトの数字(R、S)のペアであるため、署名の長さは64バイトです。
数字はリトルエンディアンで表示されます。
ハッシュ関数として、SHA-512が使用されます。
署名する際、乱数は生成されず、代わりに、秘密鍵のSHA-512ハッシュの右半分が使用され、署名されるデータと結合されます。
素数も使用されます。
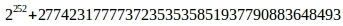
基点に乗算してゼロを与えるように基点を選択するために使用します。
おわりに
明らかに、この実装で最も遅い場所は、加算操作の分割です。 実際、ref10で行われているように、数論の最新の進歩とEdDSAパラメーターの詳細を使用して、完全に除外できます。 ただし、これにより実装が大幅に複雑になり、明確性が低下します。したがって、実際の実際的なニーズが発生した場合にのみこれを行う必要があります。 現在、I2PでのEdDSA署名の検証は、たとえばEl-Gamalスキームによる暗号化と比較すると、かなりまれなイベントです。
独自の暗号化を実装することは非常に悪い考えであると考えられています。 ただし、実際の実装が理解しにくい方法を使用する方が少し良いようです。 さらに、この記事は、問題の底辺にたどり着くことに興味のある人にとって有用な場合があり、実用的なコードの作業がこれに役立ちます。