この記事は、Javaの線形代数方程式系を解くためのガウスアルゴリズムの実装に専念しています。
理論情報
数学的理論を考えてください。 線形方程式のシステムには、1つの解、無限に多くの解がある場合や、互換性がない場合があります(解がない場合)。 システムに無限に多くのソリューションがある場合、すべてのSLAEソリューションメソッドが2番目のケースに対処できるわけではありません。 たとえば、Cramer法と行列法は適用できませんが、Gauss法を使用できます。
アルゴリズムは2つの段階に分けることができます。
第1段階では、
基本行列変換の使用により、主対角線の下または上にゼロが形成されます。 第二段階では、最後から未知のものが発見されます。 詳細な理論については、リンク:
Gauss methodを参照してください。 実装に移りましょう。
実装
問題のステートメントから始めましょう。
- 一般化されたプログラミング手法を使用して、データ構造の形で線形連立方程式を実装するプログラムを作成する必要があります。 システムには、 Numberクラスから派生したタイプの係数( Float 、 Integer 、 Doubleなど)が含まれている必要があります
- 入力を受け取ると、システムのデータ構造が主対角線の下にゼロを形成するアルゴリズムをプログラムします
各方程式を実装するインターフェースを書くことから始めましょう。
package gauss; public interface Gauss<N extends Number, T extends Gauss<N, T>> { public void addEquation(T item); public void mul(N coefficient); public N findCoefficient(N a, N b); public N at(int index); public int size(); }
ここですべてが明確になるはずです
。Nは Numberの子孫、
Tはこのインターフェイスを実装する型(再帰ジェネリック)です。
addEquation(T item)メソッドを使用すると、
アイテム方程式の各要素を各要素に追加できます。 他の方法も同様に機能します。
次に、連立方程式のクラスを考えてみましょう。 以下のリストでわかるように、これはGaussインターフェースのように汎用的であり、それらを含む方程式のプライベートリストに簡単にアクセスするためのメソッドが含まれています。
package gauss; import java.util.ArrayList; import java.util.List; public class LinearSystem<N extends Number, T extends Gauss<N, T>> { private List<T> list = new ArrayList<T>(); public T get(int index){ return list.get(index); } public void push(T elem){ list.add(elem); } public int size(){ return list.size(); } public N itemAt(int i, int j){ return list.get(i).at(j); } }
これで、方程式の構造の「特殊なケース」の実装を開始できます。 インターフェイスを実装するクラス
MyEquationを作成します。
数値の後続を
超高精度の Floatクラスにします(実際には、
Doubleを使用することをお
勧めします )。
addEquation(MyEquationアイテム)メソッドは
ListIteratorクラスのオブジェクトを使用するため、
反復リストの要素を
変更できます。
package gauss; import java.util.ArrayList; import java.util.List; import java.util.ListIterator; import java.util.Random; public class MyEquation implements Gauss<Float, MyEquation> { private List<Float> equation = new ArrayList<Float>(); public List<Float> getEquation(){ return equation; } public void generate(int size){ if (size < 2) size = 2; this.equation.clear(); for (int i = 0; i < size; i++){ Random random = new Random(); this.equation.add((float) (random.nextInt()%10) + 1); } } @Override public int size(){ return equation.size(); } @Override public void addEquation(MyEquation item){ ListIterator<Float> i = equation.listIterator(); ListIterator<Float> j = item.getEquation().listIterator(); for(; i.hasNext() && j.hasNext();){ Float a = i.next(); Float b = j.next(); i.set(a + b); } } @Override public void mul(Float coefficient){ for(ListIterator<Float> i = equation.listIterator(); i.hasNext();){ Float next = i.next(); i.set(next * coefficient); } } @Override public Float findCoefficient(Float a, Float b){ if (a == 0.0f) return 1.0f; return -b/a; } @Override public Float at(int index){ return equation.get(index); } }
これで、方程式系を実装する完全なデータ構造ができました。 Gaussインターフェイスを実装するオブジェクトを受け取るアルゴリズムを作成し、必要なメソッドを呼び出すと、マトリックスが目的の形式になります。
package gauss; public class Algorithm<N extends Number, T extends Gauss<N, T>> { LinearSystem<N, T> list = null; public Algorithm(LinearSystem<N, T> system){ list = system; } public void calculate() throws NullPointerException, ArithmeticException{ if (list == null){ throw new NullPointerException("LinearSystem<N, T> instance equal null"); } if (!checkSystem(list)){ throw new ArithmeticException("Incorrect system for Gauss Method"); } for(int i = 0; i < list.size() - 1; i++){ for(int j = i + 1; j < list.size(); j++){ N k = list.get(j).findCoefficient(list.get(j).at(i), list.get(i).at(i)); list.get(j).mul(k); list.get(j).addEquation(list.get(i)); } } } private boolean checkSystem(LinearSystem<N, T> system){ if (system.size() < 2) return false; for(int i = 0; i < system.size(); i++){ if (system.get(i).size() != (system.size() + 1)){ return false; } } return true; } }
アルゴリズムは単純で、目的の係数を見つけ、i番目の行(i = 0..n-1)に乗算し、j番目の行(j = i..n)に追加します。 アルゴリズムは
findCoefficient 、
mulおよび
addEquationメソッドがどのように実装されているかを正確に知らないことに注意してください。これにより、コードの柔軟性が
高まります。 必要に応じて、方程式(行)の操作方法を変更します。上記の3つの方法の実装のみが変更され、メインアルゴリズムは変更されません。
ほとんどすべて。 これをすべて
mainメソッドで実行することは残ります。
import gauss.Algorithm; import gauss.MyEquation; import gauss.LinearSystem; public class Main { private static final int DEFAULT_EQUATIONS_NUMBER = 2; private static final int DEFAULT_VARIABLES_NUMBER = 2; public static void main(String args[]){ LinearSystem<Float, MyEquation> list = generateSystem(); printSystem(list); int i, j; Algorithm<Float, MyEquation> alg = new Algorithm<Float, MyEquation>(list); try{ alg.calculate(); }catch (NullPointerException e){ System.out.println(e.getMessage()); System.exit(0); }catch (ArithmeticException e){ System.out.println(e.getMessage()); System.exit(0); } Float [] x = new Float[DEFAULT_EQUATIONS_NUMBER]; for(i = list.size() - 1; i >= 0; i--) { Float sum = 0.0f; for(j = list.size() - 1; j > i; j--) { sum += list.itemAt(i, j) * x[j]; } x[i] = (list.itemAt(i, list.size()) - sum) / list.itemAt(i, j); } printSystem(list); printVector(x); } public static LinearSystem<Float, MyEquation> generateSystem(){ LinearSystem<Float, MyEquation> list = new LinearSystem<Float, MyEquation>(); int i; for (i = 0; i < DEFAULT_EQUATIONS_NUMBER; i++){ MyEquation eq = new MyEquation(); eq.generate(DEFAULT_VARIABLES_NUMBER + 1); list.push(eq); } return list; } public static void printSystem(LinearSystem<Float, MyEquation> system){ for (int i = 0; i < system.size(); i++){ MyEquation temp = system.get(i); String s = ""; for (int j = 0; j < temp.size(); j++){ s += String.format("%f; %s", system.itemAt(i, j), "\t"); } System.out.println(s); }System.out.println(""); } public static void printVector(Float [] x){ String s = ""; for (int i = 0; i < x.length; i++){ s += String.format("x%d = %f; ", i, x[i]); }System.out.println(s); } }
この奇跡を実行して、作品の正しさを確認しましょう...
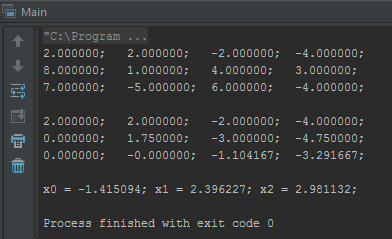
以上です。
ソースはgithubでダウンロードできます。
おわりに
Gaussメソッドは、一般化されたプログラミングにはあまり適していません(ご覧のとおり、逆方向への移動は個別に実行されました)が、インターフェイスとジェネリックの使用方法をよりよく理解するのに役立つ独特の実装が登場しました。
使用された文献のリスト: