スティーブン・ウルフラムの本「ウルフラム言語入門」

スティーブン・ウルフラムの「本を書いた—ウルフラムの言語を教えるために 」翻訳後。
Kirill Guzenkoに感謝します。

---

「Wolfram言語入門」という本は、 ハードコピー 、 無料のオンライン 、 その他の形式で利用できます。



いつか別の本を書くかどうかわかりませんでした。 私の最新の本-A New Kind of Science-は 、10年以上にわたる集中的な研究に費やしたもので、これまで行ったすべての中で最大のプロジェクトです。

しかし、少し前に別の本を書く必要があることに気づきました-プログラミングに精通していない人を紹介する本で、 Wolfram言語とこの言語が提示するコンピューティング分野の考え方を紹介する本です。

その結果が、今日出版されている初級Wolfram言語の本です。 また、インターネットや他の形式でも自由に利用できます 。



この本の目的は、ゼロから人々を導いて、Wolfram言語について十分に知って、それを定期的に使ってやりたいことすべてのためのプログラムを作成できるようにすることです。 そして、「ゼロ」と言うとき、私は本当に「ゼロ」を意味します。 この本は皆のためです。 プログラミング、数学（算術の基本を除く）、またはその他の分野の知識を意味するものではありません。 彼女は最初からリードし、さまざまなことを説明しています。 私はそれを大人と子供の両方に適したものにしようとしました。 12歳以上の普通の子供にはとても適していると思います。

過去には、そのような本の存在は不可能でした。 その実装に必要な技術はまだ存在していませんでした。 真面目なプログラミングは常に大変な作業であり、実際の概念と結びつける良い方法はありません。 しかし、今ではWolfram言語があります。 その作成には30年かかりました。 しかし、現在では十分な量の組み込みの知識が含まれており、プログラミングプロセスは十分に自動化されており、知識のない人から計算可能な人の境界に人を導くことができます。



しかし、それを行う方法は？ 何をどの順番で説明する必要がありますか？ この本を書くことになった問題がありました。 少し前に、 プログラマー向けの簡単な紹介を書きました。30ページほどで、Wolfram言語の基本的なアイデアをすでにプログラミングに慣れている人々に紹介しています。 しかし、プログラミングについて何も知らない人はどうでしょうか？

長年にわたり、私はこれらの人々に現在のWolfram言語が何であるかを示す様々な方法を見つけてきました。 それで、私はこの経験で何をする必要があるかをこの本で説明しました。

これは対話です

本質的に、この本は読者とコンピューターの間の会話です。 Wolfram言語には、すべてが正常に機能するようにする2つの重要なことがあります。 まず、言語はシンボリックであるため、 color 、 image 、 graphなど、 処理するすべてのものをダイアログボックスに表示できます。 そして第二に、言語は純粋に機能的であるため、その中のすべてが安定しており、入力はすべて自給自足の構造になります。



また、Wolfram言語に組み込みの知識が含まれていることも非常に重要です。これにより、実際の計算をすぐに開始できます。





視覚化も同様に重要です-したがって、何が計算されたかを簡単に確認できます。

どこから始めますか？

では、どこから始めますか？ 算術に関する本の最初のページ -結局のところ、これは誰でも計算の仕組みを見ることができる領域です：



Wolfram言語の「 単語 」の一部を理解するのに役立つ辞書 （語彙）と呼ばれるセクションがあります。 また、 演習 （演習）もあります。

さて、算術は終わりました。次はどこに行きますか？ 私は関数の表現に直行し、算術概念を通してそれらを紹介することにしました。 プラスは、関数の概念は読者にとっては新しいかもしれませんが、それらが実行する操作（算術演算）はすでによく知られていることです。



Plus関数が明らかになるとすぐに、特別な紹介を必要としないMaxなどの関数にすぐに切り替えることができます。 Max関数は特に興味深いことは何もしません。 次に紹介するより興味深い機能はRandomIntegerです 。これは、人々が何度も何度も使用して、それが与えるものを確認するのが好きです。

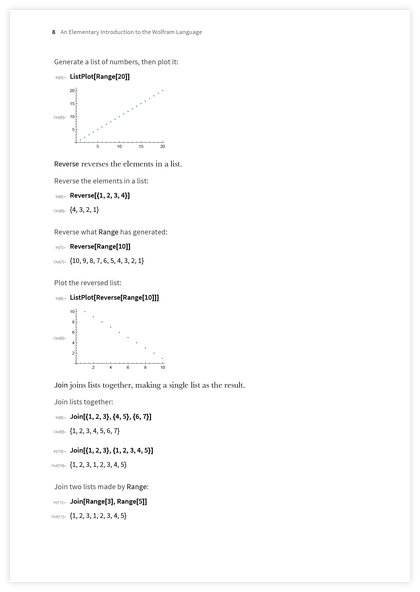
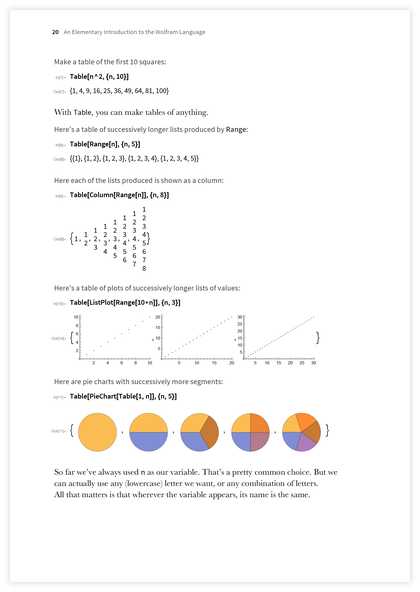
それでは、次は何ですか？ 答えは明らかです-リストを入力する必要があります。 しかし、リストをどうするか？ それらから要素を選択することは特にエキサイティングではないようであり、これが重要であるという理解はすぐには得られません。 したがって、リストを操作するための最初の機能であるListPlotを導入することにしました。 視覚化から始めるのは素晴らしいことです。また、これはほんの小さなコードを入力して、最終的により大きくて興味深いものにする方法の良い例でもあります。



実際、最も単純な例の中で最も優れているのはRange関数であり、これもここで説明しました。 範囲は、コンピューターが実際に何かを計算していることを示し、理解しやすい結果を生成する素晴らしい方法です。

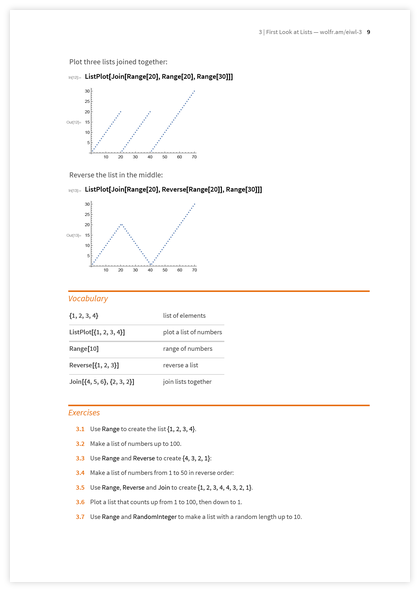
さて、今、私たちは機能とその共同作業のアイデアを統合する必要があります。 Reverse関数は実際にはあまり一般的ではありませんが、理解するのは非常に簡単です。 次に、 Join関数を紹介します。



良いニュースは、 Reverse 、 Range 、およびJoinを使用すると 、完全に自給自足であり、さまざまな計算を実行できるある種のマイクロ言語があることです。 そして、もちろん、計算を行うと、シンボリックまたはグラフィック形式で結果をすぐに見ることができます。



次のセクションでは、 視覚化とリストの操作について説明します。これにより、前述の内容が統合され、実際に役立つさまざまな機能が紹介されます。 次に続くのはTableで、これにはループなどの便利な機能を含む非常に強力で一般的な機能があります。

反復子のない単純なバージョンのTableから始めます。 Tableは数字のリストと同じ方法でグラフィック要素のリストを表現できることは当然だと思います（もちろん、これができるという事実は、Wolfram言語の根本的に象徴的な性質の結果です）。



次の大きなステップは、 Tableに変数を入力することです。 私はこれをどのように行うかについて多くのことを考え、純粋に象徴的なバージョンでこれを最初に示すことが最善であると判断しました。 最後に、関数を既に紹介しました。シンボリックバージョンでは、変数の出所をすぐに確認できます。 しかし、変数を含むテーブルを導入したので、外に出て、「リアルコンピューティング」と呼ばれるものを実行することができます。

本へのゲートウェイ

本の最初の数セクションでは、計算の材料は主に数字とリストでした。 さらに、計算に使用できるものが他にもあることを示したいと思います。 最初の例のように、 色を選択しました。 （a）誰もが自分の存在を知っている、（b）計算を実行できる、（c）助けを借りてカラフルな結果を得ることができる（！）ため、色は良い選択です。



色が完成したら、 グラフィックオブジェクトに移ります 。 座標の概念は導入しなかったため、個々のグラフィックオブジェクトを表示できるのは、それらの位置に関する情報なしです。



そして、3次元の図形に触れない理由はまったくありません。さらに、それらに触れます。



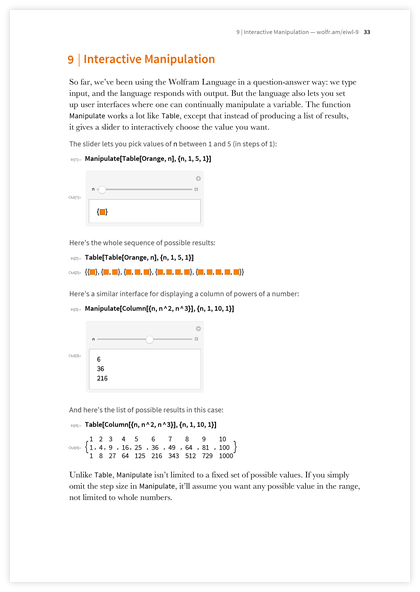
これで、「高度な」何か、 インタラクティブな操作の準備ができました。 構文の点では、 Tableと多くの類似点がありますが、ここでは完全なインタラクティブユーザーインターフェイスが得られます。 また、グラフィックスを導入したため、インターフェイスの一部になる可能性があります。 人々は、多数の異なるプログラムでインタラクティブなインターフェースを見ました。 私の経験では、彼らが自分でゼロから作成する能力に非常に感銘を受けることを示しています。



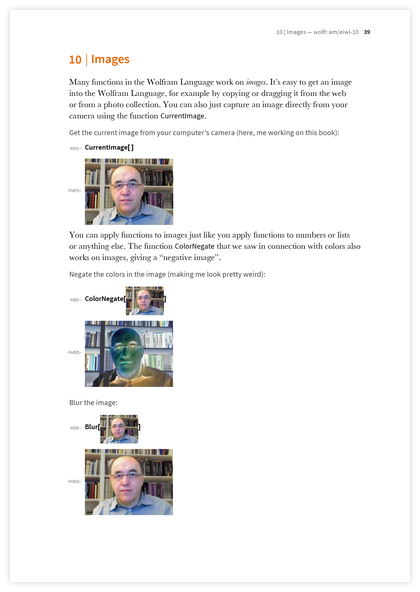
この本で次に紹介するのは、おそらく驚くべきことですが、画像処理です。 はい、画像処理の背後には多くの複雑な計算があります。 しかし、Wolfram言語では、すべてが内部に隠されています。 そして、人々はBlur 、 ColorNegateのような機能を見るだけで、その目的は簡単に理解できます。

また、人々、特に子供は、必要に応じて画像をドラッグするだけで画像を使用して計算を実行できることを奨励しています。 実際、これは大量のデータが外部からプログラムに入力される本の最初の例です（セクションのサンプル画像が必要だったので、ウェブカメラで本の作業をしました）。



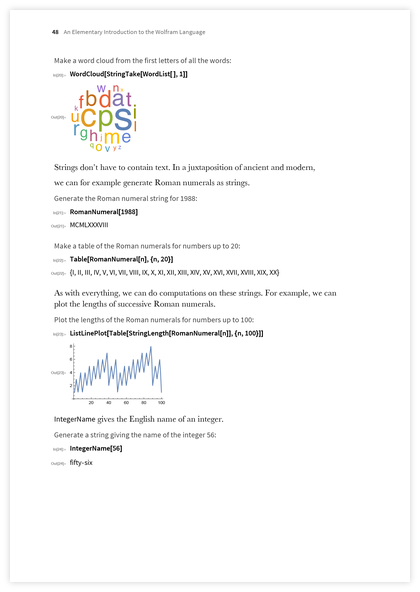
それから私は行とテキストについて話しました。 文字列操作は非常に退屈です。 しかし、Wolfram言語には、ウィキペディアの記事から単語の雲を視覚化するか、さまざまな言語で人気のある単語を検索するかに関係なく、あなたができる多くの興味深いことがあります。



次に、 音と音符からシーケンスを作成する方法について説明しました。 もちろん、印刷された本ではそれらを聞くことはできませんが、小さなアイコンは私たちが何を扱っているのかをある程度示しています。



「グラフィックの直後に音に触れないのはなぜですか？」と尋ねるかもしれませんが、まず第一に、興味を維持するためにいくつかのことを混ぜることが良いと思いました。 ただし、異なる領域の間には依存関係の特定のチェーンがあります。 たとえば、音符の名前は文字列として指定されるため、最初に文字列に言及する必要があります。

以下は、 配列、またはリストのリストです。 その後- 座標とグラフ 。 まず、座標があまりにも「数学的な」ものであることが心配でした。 しかし、特に配列を調べた後、座標はもはや非常に複雑な概念ではないようです。 また、2次元座標の概念を検討したので、3次元に移行することは難しくありません。



本のこの時点で、人々はすでにWolfram言語で本当に役に立つことをする方法を知っています。 それで次のセクションでは、ある種の間奏をもたらしました-メタセクションの一種で、 Wolfram言語のボリュームを理解し、特定のトピックや機能に関する情報を見つける方法も示します。



抽象コンピューティングを導入したので、今度は実際のデータについて説明し、Wolfram LanguageがWolfram | Alphaで提示する膨大な量のデータにアクセスする方法を示します。



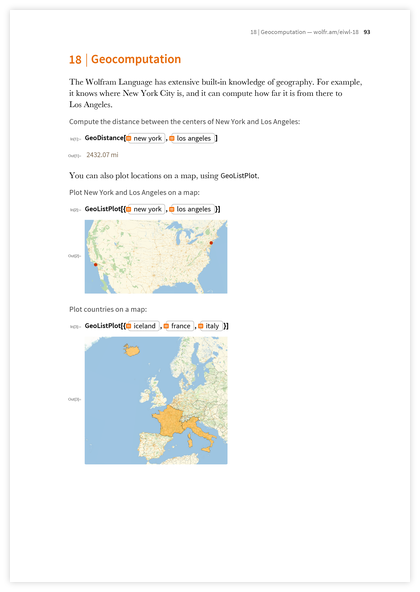
多くの実世界のデータにはユニットが含まれているため、次のセクションではユニットの操作について説明します 。 これが完了したら 、地理計算セクション（地理に関連する計算）に触れます。たとえば、地球上のポイント間の距離を検索したり、マップを描画したりできます。



その後、 日付と時間についてお話します 。 これは特に面白くて有用なトピックではないと思うでしょう。 しかし、これは実際にはユビキタスな実際のコンピューティングの非常に良い例です。



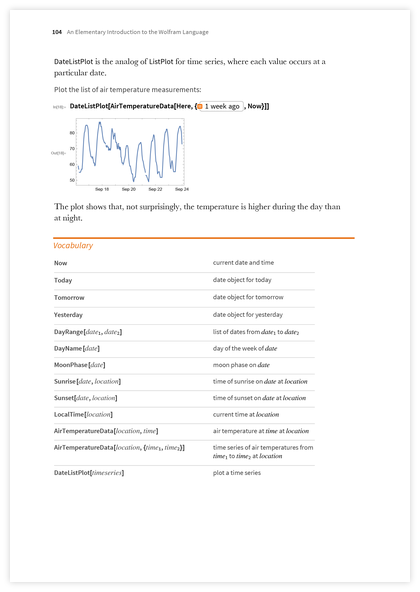
Wolfram言語は非常に膨大な言語です。 しかし、それは常に何度も何度も使用されている少数のアイデアに基づいています。 本の最も重要なタスクの1つは、これらのアイデアをカバーすることです。 そして次のセクション- オプションについて -は、実際に絶え間なく発生する1つの簡単なアイデアをカバーしています。



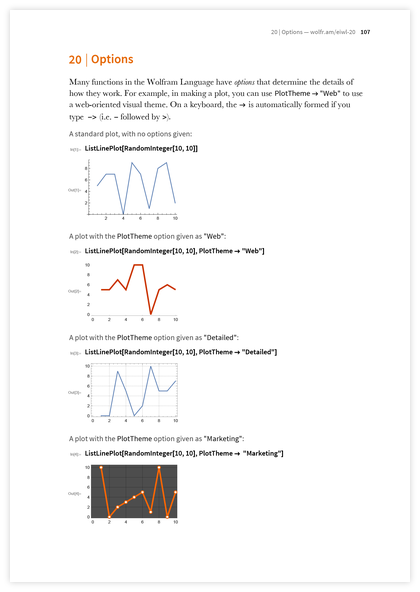
オプションの後、私たちはしばしば複雑なトピックとして見られる何かについて話す準備ができています： グラフとネットワーク 。 しかし、私の経験では、人々は日常生活でかなり多くのグラフとネットワークに直面しているため、Wolfram言語でそれらを理解するのに大きな問題はないことを示しています、これはシンボリックオブジェクトの別の例です。



グラフとネットワークに続いて、一見非常に複雑なトピックである機械学習を開始する準備ができました。 しかし、内部の機械学習アルゴリズムが複雑であっても、Wolfram言語でそれを実装する機能自体は非常に理解しやすいものです。 そして、素晴らしいことは、彼らと一緒に多くの例を感じたことで、機械学習の重要なアイデアの非常に良い直感的なアイデアを得ることができるということです。



本を通して、私は可能な限り単純な方法で物事を提示しようとします。 ただし、これにより、すでに取り上げたトピックをより詳細に調べる必要が生じる場合があります。 「数値の詳細」と「その他の視覚化」はこの事実を示す2つの例であり、すでに通過した概念を説明していますが、これらの領域をより完全に理解するには、新しいレベルでそれらに戻る必要があります。

関数型プログラミング

次のいくつかのセクションでは、 関数型プログラミングの重要かつ信じられないほど強力なトピックを明らかにします 。 過去において、関数型プログラミングは一般的に複雑なものと見なされ、プログラミングを習い始めたばかりの人々に教える価値のあるものではありませんでした。 しかし、Wolfram言語は状況を変えたと思います。そして今、はるかに理解しやすい言語で関数型プログラミングを説明することが可能になりました。 関数を適用するプロセスについての抽象的な会話から始めることにしました。



まず、 純粋な匿名関数についてお話したいと思います 。 原則として、もっと早く話をすることができますが、その前に、関数が一般的にどのように使用されるかを人々に示すことが重要だと思います。



次のセクションでは、関数型プログラミングの真の力のいくつかの兆候に既に気づくことができます。 一般的に、 NestListやNestGraphなどの関数は、かなり複雑で抽象的に見えるかもしれません。 しかし、本のこの時点では、十分な数のWolfram言語構成体を調べたので、簡単に説明できる多くの具体的な例があります。



次のいくつかのセクションでは、純粋な機能を理解するときに開かれる言語の領域について説明します。 少ないアイデアから生まれる多くの強力なプログラミング方法があります。



関数型プログラミングの後、次の大きなトピックはテンプレートとパターン指向プログラミングです。 以前にそれらについて話をすることはできましたが、今のところそれらの必要はありません。



Wolfram言語でテンプレートを非常に強力にする基本的なものがあります：シンボリック式に基づいた言語のあらゆるものに対する単一の構造です。 Wolfram言語の仕様を書いたら、文字式から始めます。 そして、理論計算機科学または純粋数学の専門家向けの本を書いたなら、確かに同じことをするでしょう。

シンボリック式は理解しにくい概念ではありません。 Wolfram言語が実際に実際にどのように機能するかがわからないだけで、理論的基礎を研究する動機付けが難しい。 しかし、今ではそれらについて話をするのが理にかなっています。特に、テンプレートを使用してその栄光の作品をすべて見ることができるからです。

スタック全体

本のこの時点で、たとえばWebアプリケーションをデプロイする方法を検討する準備ができました。 しかし、その前に、他に考慮すべきことがあります。 協会について、それから自然言語認識について話します。 内部的には、言語認識システムは非常に複雑なものです。 しかし、Wolfram言語レベルでは認識は使いやすいですが、他の事柄とどのように関係するかを見るためには、純粋な機能について話す必要があります。



さて、これですべてがインターネットでの展開について話す準備ができました 。 そして現時点では、人々は、世界と共有できる便利なアプリケーションソフトウェア構成を作成する機会があります。



すべて220ページほどかかりました。 しかし、私にとっては、これは驚くほど少数のページであり、ゼロから最初からWebアプリケーション開発の専門分野に進むことができます。 特定の種類のアプリケーションについてのみ説明した場合、これはそれほど印象的ではありません。 しかし、ほとんどすべての種類の計算を実行できる非常に一般的な形式のアプリケーションについて話しています。

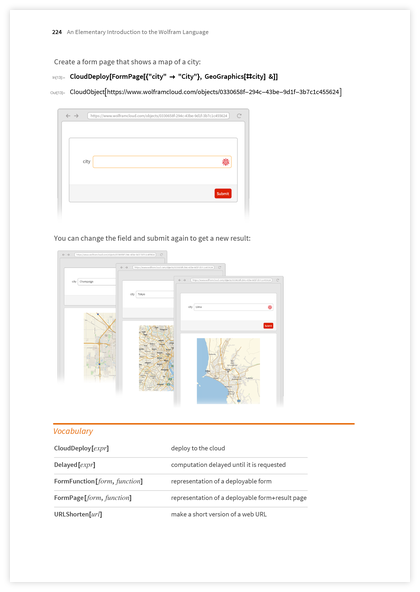
変数への値の割り当て

C ++やJavaなどの従来のプログラミング言語に関する本を開いた場合、最初に出くわすトピックの1つは、変数に値を割り当てることです。 しかし、私の本では、 38番目のセクションでのみこのトピックを引用しています。 ある意味、これは奇妙に思えるかもしれませんが、実際にはそうではありません。 結局のところ、Wolfram言語では、変数に値を割り当てることなく本格的なWebアプリケーションをデプロイするなど、驚くほど多くのことができます。

そして実際、これがWolfram言語の習得が非常に簡単な理由の1つです。 実際、変数に値を割り当てない場合、各コードは独立し、常に同じ動作を示します。 しかし、変数への値の割り当てを開始するとすぐに、非表示の状態が表示され、変数の現在の値に応じてコードが異なる処理を実行します。

それにもかかわらず、変数とテンプレートへの値の割り当てについて話し合ったとき、Wolfram言語でますます複雑な機能を導入できる独自の関数の定義に移る準備ができています。



この時点で、読者はWolfram言語の用語と基本概念について完全にガイドされています。 しかし、本の最後のいくつかのセクションでは、いくつかの重要な応用ポイントについて説明しています。 文字列パターンと置換に関するセクションがあります。 次のセクションでは、 データとコードをローカルおよびクラウドに保存する方法について説明します 。 次に、 インポートとエクスポートのセクション。 次に、 データコレクション（セット）のセクション。 Wolfram言語を使用するすべての人がデータのコレクション（セット）を必要とするわけではありませんが、大量の構造化データを処理する必要がある場合、このセクションは非常に役立ちます。 そしてそれらはすべて、Wolfram言語でさまざまなアイデアがどのように実装されているかの興味深い例です。

エッセイセクション

本の最後には、さまざまなトピックに関するエッセイのセクションがあります： 良いコードを書くこと、 デバッグ すること、それがプログラマーであると感じる方法について。 これらのセクションの目的は、この本を読んだ結果として生じた思考方法を開発し、いくつかの抽象的なアイデアに結び付けることです。

プレゼンテーションの構成

最初に言ったように、この本は基本的に口語的なスタイルで書かれています。 ほとんどすべてのセクションで、 質問と回答と技術的詳細 という 2つの追加部分を追加しました。 質問と回答を含む部分の目的は、人々が最も頻繁に遭遇するこれらの質問への回答を、ストーリーテリングのメインラインから気を散らすことなく提供することです。



質問にはいくつかの種類があります。 一部は、前述の機能拡張に関するものです。 一部は、これらすべての背後にあるものについてです。 また、いくつかの質問（「べき乗とはどういう意味ですか？」）読者によっては単純すぎるように見えるかもしれませんが、すべての読者にとってはそうではありません。

質問と回答を含む部分に加えて、技術的な詳細を含む部分を含めることは合理的であるように思えました。 彼らの目標は、特定の分野に既に十分に適応している人々に技術情報を提供し、彼らの知識を本の資料と組み合わせることができるようにすることです。

演習

ほとんどのセクションで示されている他の部分は、演習のコレクションです。 それらの大部分は、「 Nを作成するコードを書く 」という形式で表示され、「 このコードのより単純な同等物を見つける 」という形式はほとんどありません 。



印刷された本の最後には、すべての演習への答えがあり、Webバージョンには追加の演習があります。 もちろん、そこに提示される答えは可能なものの1つだけであり、これが唯一の正しい答えである場合、状況はほとんど発生しません。



演習を書くことは私にとって興味深い経験でした。実際、これは、たとえば人工知能と通信する方法についての私の考えの文脈において非常に重要です。 結局のところ、ほとんどの演習では基本的に「 このテキストを英語で取り、Wolfram言語コードに変換します」 と書かれています 。 簡単なことですが、英語は自分自身を説明するのに適しています。 しかし、タスクが難しいほど、英語で説明するのは難しくなります。 一般に、本を書くとき、英語で書くよりもWolfram言語のエクササイズに答える方がはるかに簡単な状況にしばしば遭遇しました。

ある意味では、これは非常に優れています。なぜなら、Wolfram言語はアイデアを表現するのに非常に適しているからです。 英語で簡単に表現できるものもありますが、Wolfram | Alphaでの解釈に合格できます。 しかし、Wolfram言語にはもっと多くの構造と精度が必要なものがたくさんあります。

本？

ある意味では、はるかに柔軟な構造でウェブ形式で何かを作成するのではなく、印刷可能な本を書くのは奇妙に思えるかもしれません。 しかし、私にとっては、この本の概念が非常に役立つことがわかりました。 はい、リンクをたどって多くの情報を取得できるWebサイトを作成できます。 - , , , , .

, - . - , - . , , - — — .

, Wolfram Language, . , , ( ), , .. , . , : , Wolfram Language .

« ». . Wolfram Language — . , , , , . , .

, , , , . , ; , .

, , , Wolfram Language, . , , .

Wolfram Language. 1988 , Mathematica, . : , . 767 . 10 , «» 1488 . , — , .



, , , , . , , , 50 000 .

, Mathematica , , , , . , Wolfram Language , , .

, , Wolfram Language ( Mathematica) . , , , . , , Wolfram Language Mathematica , .

?

, - , . , , , Wolfram Language , , . , . , , , . .

: " ? ". , , , , , . . .

この本を書くのは本当に楽しかったです。人々がそれを読んで興味を持ち、 Wolfram言語ですばらしいものを作成する方法を学ぶことを願っています！