プログラミングでバイナリツリーのトピックに最初に出会ったとき、私はすぐにHabréでのほとんどすべての質問に対する答えを見つけましたが、時間がたつにつれて、さらに質問があり、最近このリソースでまだカバーされていないトピックを見つけました-これは2です-3-4本の木。 2-3ツリーのトピックに関する
優れた記事があります。ここでは
、 「ヒープとは」、「2〜3ツリーとは」という質問への回答、および構造の基本的な操作に関する情報を見つけることができます。メイントピックへ。
したがって、2-3からの2-3-4ツリーの主な違いは、3つ以上の子ノードを含めることができることです。これにより、4つのノード(4つの子ノードと3つのデータ要素を持つノード)を作成できます。 テキストの下のGIFで視覚的に違いを見ることができます最初のスライドは2-3ツリー、2番目のスライドは2-3-4を示しています。
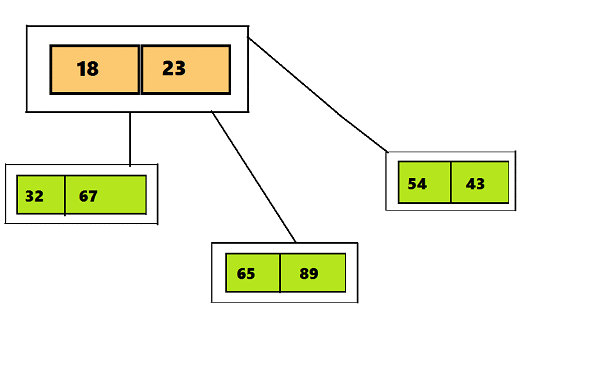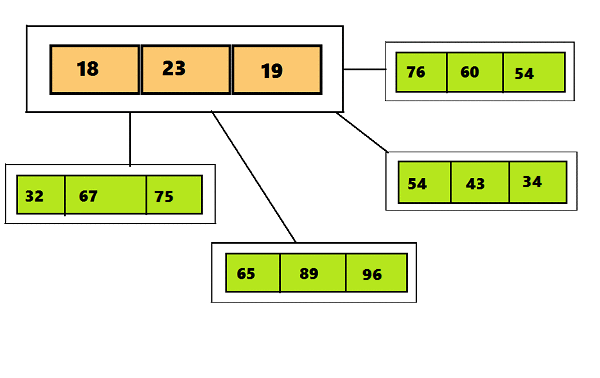
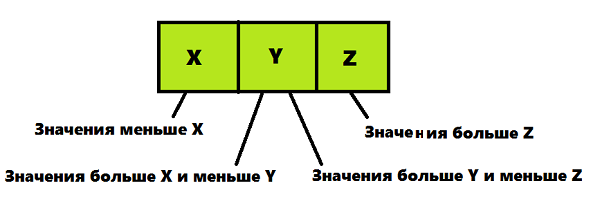
ツリーのノード2-3-4に配置されたデータ(および2-3ツリーに配置されたデータ)にはいくつかの要件があります-この情報の短い画像は、テキストの下の図で見ることができます:
- ノードに2つの要素が含まれ、2つの子ノードがある場合、ノードには1つの要素が含まれている必要があり、その値は左の子ノードの値より大きく、右の子ノードの値より小さい必要があります
- ノードに2つの要素が含まれ、3つの子ノードがある場合、ノードは次の関係を満たす必要があります。Xの値は、左の子ノードの値より大きく、平均子ノードの値より小さい。 Zの値は、中間の子ノードの値より大きく、右側の子ノードの値より小さいです。
- ノードに3つの要素が含まれ、4つの子ノードがある場合、ノードは次の関係を満たす必要があります。Xの値は、左の子ノードの値より大きく、左の中央の子ノードの値より小さい。 Y値は、左中央の子ノードの値より大きく、右中央の子ノードの値より小さい。 Zは、右の中央の子ノードの値よりも大きく、右の子ノードの値よりも小さいです。
- シートには、1つ、2つ、または3つの要素を含めることができます。
2-3ツリーと比較した2-3-4ツリー
の主な利点は、要素の挿入と削除の標準操作がより少ないステップで実行されることです。
主な欠点は、必要なメモリ量です。2-3-4ツリーには、どこかに格納する必要がある要素がより多く含まれるため、より多くのメモリを消費する必要があるためです。 この問題を解決するために、特別な種類の
赤黒二分木 (赤黒木)を使用できますが、それらについては後で説明します。
2-3-4ツリーの基本操作の原理を説明する前に、「C ++でのデータ抽象化と問題解決」という本のコードの例、クラスが2-3-4ツリーをどのように記述できるかを示します。
lass TreeNode { private: TreeltemType smallltem, middleltem, largeltem; TreeNode *leftChildPtr, *lMidChildPtr, *rMidChildPtr, *rightChildPtr; friend class TwoThreeFourTree; };
2-3-4ツリーで検索
ツリーの要素2-3-4の検索アルゴリズムは、ツリーの要素2-3の検索アルゴリズムに類似しています(検索アルゴリズムの効率
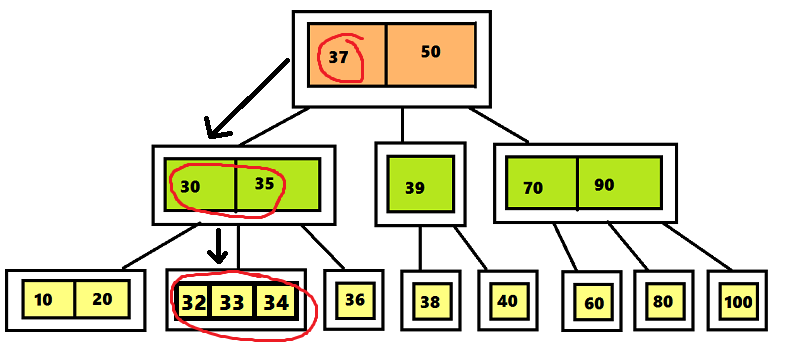
ツリー2–3の順序はO(log n)です)、アルゴリズムは同じであると言えますが、拡張されています。 一番下の行は、たとえば、ツリーで値31を含む要素を検索するには、ルート31の値が37より小さいため、ルートの左のサブツリーを調べるとよいでしょう。次に、ノード31の平均サブツリー<30 35>が調べられます。 35.数値31は32より小さいため、ノード<32 33 34>の左の子ノードへのポインターで検索が終了します。その結果、ツリーに値31を含む要素はないと結論付けます。
2-3-4木材に挿入
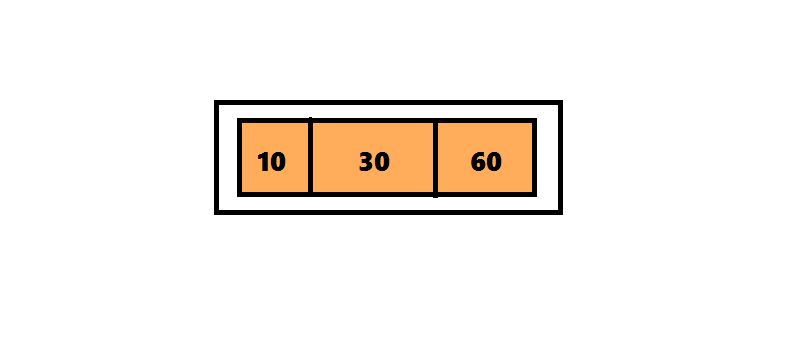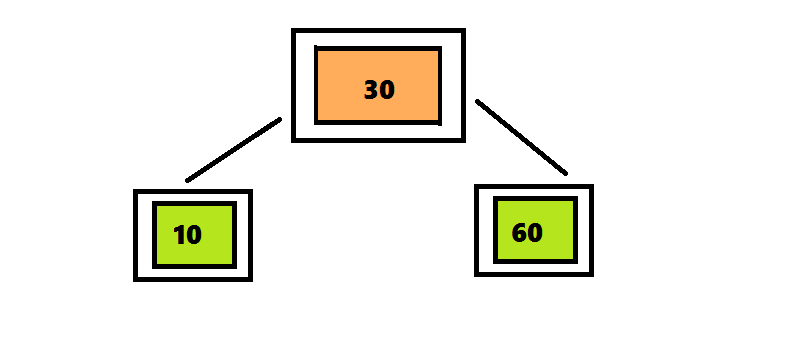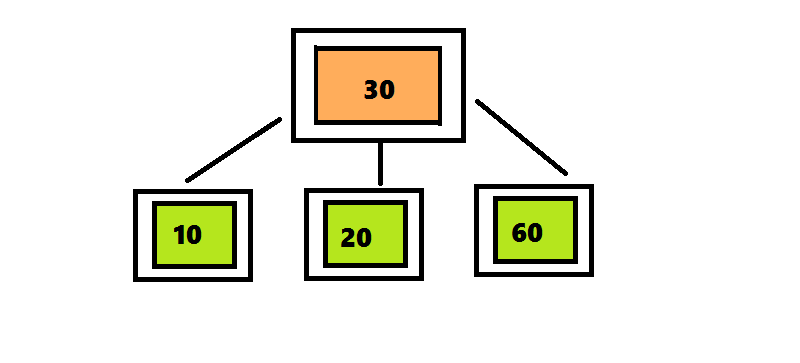
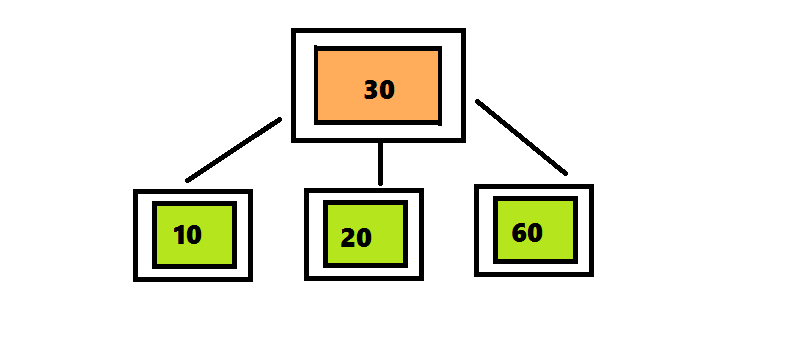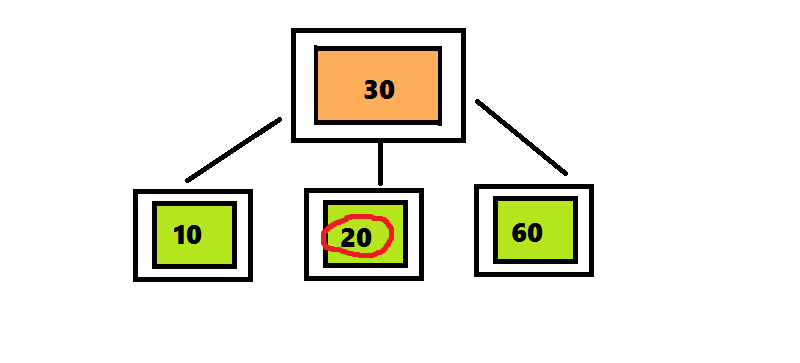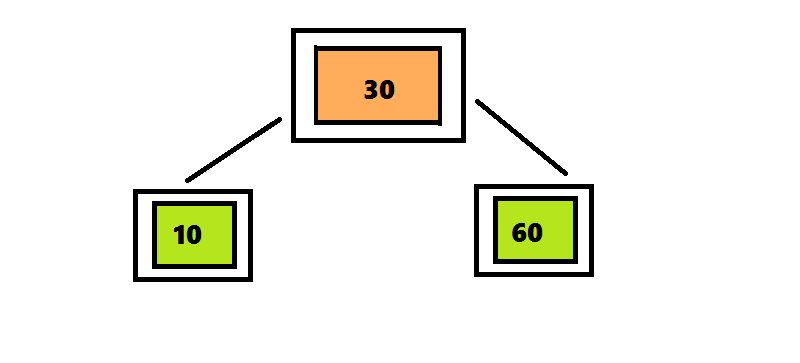
ツリー2-3-4に要素を挿入するアルゴリズムは、ツリー2-3に要素を挿入するアルゴリズムとは異なり、4つの要素を含むノードが検出後すぐに分離されます。ツリー2-3では、検索アルゴリズムはルートからシートへのパスをたどりました。そして戻ってきて、ノードを分割しました。 この戻りを回避するために、要素を2-3-4ツリーに挿入するアルゴリズムは、ルートからシートへの途中で検出されるとすぐに4重ノードを分割します。 挿入位置の検索は、ルートから始まります。これは、4つのノード<10 30 60>です。 30を上に移動して、3つの部分に分割します。 このノードはルートであるため、新しいルートを作成し、30を入力して2つの子ノードをアタッチする必要があります。 番号20は30より小さいため、ルートの左のサブツリーをチェックして、番号20の検索を続けます。
2-3-4ツリーからノードを削除する
削除アルゴリズムは、指定された要素を含むノードの最初の検索で構成されます。 次に、このノードの対称的な後継者を探しています。 次に、それらを要素と交換して、シートからの削除が常に実行されるようにします。 シートに3つまたは4つの要素が含まれる場合、その要素を単純に削除します。 主な違いは、2-3-4ツリーでは、2-3ツリーのようにルートに戻ってツリーを再構築する必要がないことです。
私の話を
前任者の言葉で終えたいと思います:「このトピックに関するコースプロジェクトを書くとき、RuNetにはほとんど情報がないことに気づいたので、興味のあるコミュニティにこのデータ構造を伝えることで、このビジネスに自分のペニーを追加することにしました。」
PS:執筆中、「C ++でのデータ抽象化と問題解決」という本から知識を引き出しました。 壁と鏡”第3版、著者:フランク・M・カラーノ、ジャネット・J・プリチャード、この記事を読むように皆さんにアドバイスします。読者の皆さん、資料に注意を払ってくれたことに感謝します。