昨年のPG Day'15 Russiaカンファレンスで、私たちのスピーカーの1人であるジョセフコンウェイが、10年以上にわたって彼が作成およびサポートしたPL / R拡張機能の使用に関する興味深い資料を紹介しました。データベース Joeのレポートに示されている資料に基づいて作成されたフォローアップ記事に注目したいと思います。 この出版物の目的は、PL / R言語の可能性を知ることです。 ここに記載されている情報がお役に立てば幸いです。
最近のビッグデータの傾向により、分析とデータの収束が促進されていますが、PL / Rはこのようなサービスを控えめに12年間提供しています! 突然あなたが知らない場合、PL / RはPostgreSQLの拡張機能であり、簡単かつ詳細な分析を簡単に取得するために、PostgreSQLから直接Rを数学計算の言語として使用できます。 拡張機能は利用可能であり、2003年以降積極的に改善されています。 サポートされているすべてのバージョンのPostgreSQLおよびすべての最近のバージョンのRで動作します。世界中の何千人もの人々が、その便利さと有効性をすでに評価しています。 PL / Rとは何かを見て、データ分析に対するこのアプローチの長所と短所を説明し、説明のためにいくつかの例を考えてみましょう。
まず、基本的な概念を定義しましょう。 Rは、統計データ処理とグラフィックス、および無料のオープンソースソフトウェア環境のためのプログラミング言語です。 また、PostgreSQLは強力で無料のオブジェクトリレーショナルデータベース管理システムであり、25年以上にわたって積極的に開発されており、その信頼性とデータの正確性および整合性により高い評価を得ています。 そして最後に、PL / R 前述のように、これはPostgreSQL用の手続き型R言語ハンドラであり、RでSQL関数を記述できます。
PL / Rの利点は何ですか? まず、数学、統計、データベース、およびWebはそれぞれ異なる専門分野であるため、PL / Rは人間の知識とスキルの開発に貢献しますが、PL / Rを使用するにはある程度すべて習得する必要があります。 第二に、この拡張機能はハードウェアの改善を促進します。大規模なデータセットの分析に耐えられるサーバーが必要だからです。 第三に、ネットワーク全体に大きなデータセットを転送する必要がなくなり、スループットが向上するため、処理効率が向上します。 第4に、分析が確実に順次実行されることを確認できます。 第5に、PL / Rは複雑なシステムを理解しやすく保守しやすくします。 最後に、豊富な機能と巨大なエコシステムにより、PL / RはRを拡張します。
しかし、もちろん、欠点もあります。 PostgreSQLユーザーは、特に単純なタスクではPL / Rが遅いことに気付くでしょう。 また、Rプログラマーにとっては、デバッグプロセスがより複雑になり、分析の柔軟性が低下します。 さらに、両方が新しい言語を学ぶ必要があります。
Rの標準関数は次のようになります。
func_name <- function(myarg1 [,myarg2...]) { function body referencing myarg1 [, myarg2 ...] }
PL / Rでの関数の作成は少し異なりますが、PostgreSQLの他のPLと似ています。
CREATE OR REPLACE FUNCTION func_name(arg-type1 [, arg-type2 ...]) RETURNS return-type AS $$ function body referencing arg1 [, arg2 ...] $$ LANGUAGE 'plr'; CREATE OR REPLACE FUNCTION func_name(myarg1 arg-type1 [, myarg2 arg-type2 ...]) RETURNS return-type AS $$ function body referencing myarg1 [, myarg2 ...] $$ LANGUAGE 'plr';
以下に例を示します。
CREATE EXTENSION plr; CREATE OR REPLACE FUNCTION test_dtup(OUT f1 text, OUT f2 int) RETURNS SETOF record AS $$ data.frame(letters[1:3],1:3) $$ LANGUAGE 'plr'; SELECT * FROM test_dtup(); f1 | f2
PL / Rでできることをすべてリストすることは困難ですが、次のようないくつかの重要なプロパティを詳しく見てみましょう。
- PostgreSQLとの互換性。
- カスタムSQL集約。
- ウィンドウ関数;
- Rオブジェクトをbytea(バイナリ文字列)に変換します。
PostgreSQLとの互換性のおかげで、Rを使用してプロトタイプを作成し、PL / Rに移動して実稼働で実行できます。 また、明確なプラスは、すべてのクエリが現在のデータベースで実行されることです。 ドライバーと接続の設定は無視されるため、dbDriver、dbConnect、dbDisconnect、dbUnloadDriverは追加の作業を必要としません。
dbDriver(character dvr_name) dbConnect(DBIDriver drv, character user, character password, character host, character dbname, character port, character tty, character options) dbSendQuery(DBIConnection conn, character sql) fetch(DBIResult rs, integer num_rows) dbClearResult (DBIResult rs) dbGetQuery(DBIConnection conn, character sql) dbReadTable(DBIConnection conn, character name) dbDisconnect(DBIConnection conn) dbUnloadDriver(DBIDriver drv)
説明のために、いくつかの例を挙げましょう。 有名な巡回セールスマンの問題を解決するためにRからPostgreSQLを使用する必要があるとします。これについては後で詳しく説明します。
tsp_tour_length<-function() { require(TSP) require(fields) require(RPostgreSQL) drv <- dbDriver("PostgreSQL") conn <- dbConnect(drv, user="postgres", dbname="plr", host="localhost") sql.str <- "select id, st_x(location) as x, st_y(location) as y, location from stands" waypts <- dbGetQuery(conn, sql.str) dist.matrix <- rdist.earth(waypts[,2:3], R=3949.0) rtsp <- TSP(dist.matrix) soln <- solve_TSP(rtsp) dbDisconnect(conn) dbUnloadDriver(drv) return(attributes(soln)$tour_length) }
そして、ここにPL / Rの同じ関数があります:
CREATE OR REPLACE FUNCTION tsp_tour_length() RETURNS float8 AS $$ require(TSP) require(fields) require(RPostgreSQL) drv <- dbDriver("PostgreSQL") conn <- dbConnect(drv, user="postgres", dbname="plr", host="localhost") sql.str <- "select id, st_x(location) as x, st_y(location) as y, location from stands" waypts <- dbGetQuery(conn, sql.str) dist.matrix <- rdist.earth(waypts[,2:3], R=3949.0) rtsp <- TSP(dist.matrix) soln <- solve_TSP(rtsp) dbDisconnect(conn) dbUnloadDriver(drv) return(attributes(soln)$tour_length) $$ LANGUAGE 'plr' STRICT;
Rが最終的に提供するものを次に示します。
tsp_tour_length() [1] 2804.581
そして、PL / Rの同じ機能:
SELECT tsp_tour_length(); tsp_tour_length
ご覧のとおり、結果は同じです。
次に、集計について説明します。 PostgreSQLの最も便利な機能の1つは、独自の集計関数を作成できることです。 PostgreSQLの集計は、SQLコマンドを使用して展開できます。 この場合、状態遷移関数と、場合によっては最終関数が示されます。 遷移関数の初期条件も指定できます。 また、PL / Rを使用してこれらのメリットを享受できます。
以下は、新しい集約を実装するPL / R関数の例です。 最近まで、PostgreSQLからこれを行うことはできませんでしたが、GROUPING SETS機能はバージョン9.5でのみ登場しましたが、PL / RではどのバージョンのPGでもこれを行うことができます。 ある生産会社の実際のデータに基づいて集約関数を作成し、四分位数と呼びます。
CREATE OR REPLACE FUNCTION r_quartile(ANYARRAY) RETURNS ANYARRAY AS $$ quantile(arg1, probs = seq(0, 1, 0.25), names = FALSE) $$ LANGUAGE 'plr'; CREATE AGGREGATE quartile (ANYELEMENT) ( sfunc = array_append, stype = ANYARRAY, finalfunc = r_quantile, initcond = '{}' ); SELECT workstation, quartile(id_val) FROM sample_numeric_data WHERE ia_id = 'G121XB8A' GROUP BY workstation; workstation | quantile
Rを使用すると、データを素敵なグラフの形式で表示できます。 この場合、ボックスダイアグラムが使用されました。

グラフは、生産ステーションの1つが他の生産ステーションよりも生産性が低いことを示しており、これを修正するための対策が必要です。
それとは別に、
ウィンドウ関数で停止する価値が
あります 。 バージョン8.4以降、PostgreSQLで利用可能であり、統計分析に最適です。 ウィンドウ関数は集計関数と似ていますが、それらとは異なり、文字列をグループ化しませんが、クエリ結果の現在の行だけでなく、現在の行に関連付けられた文字列のセットで計算できます。 つまり、データはセクションに分割され、これらのセクションをスライドして各データグループの結果を生成するウィンドウがあります。
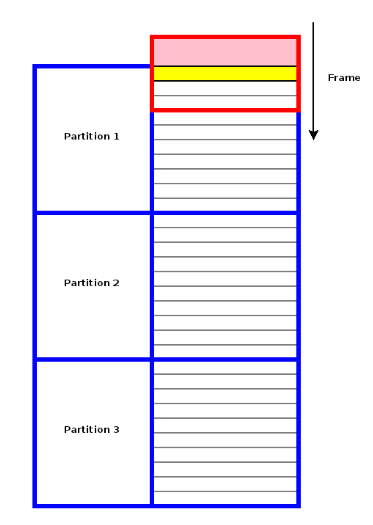
PostgreSQLはウィンドウ関数をほとんどサポートしていませんが、PL / Rでは非常に便利です。 例は次のとおりです。収益と株価をシミュレートするランダムデータテーブルを作成します。
CREATE TABLE test_data ( fyear integer, firm float8, eps float8 ); INSERT INTO test_data SELECT (bf + 1) % 10 + 2000 AS fyear, floor((b.f+1)/10) + 50 AS firm, f::float8/100 + random()/10 AS eps FROM generate_series(-500,499,1) b(f); CREATE OR REPLACE FUNCTION r_regr_slope(float8, float8) RETURNS float8 AS $BODY$ slope <- NA y <- farg1 x <- farg2 if (fnumrows==9) try (slope <- lm(y ~ x)$coefficients[2]) return(slope) $BODY$ LANGUAGE plr WINDOW;
そして、単純な回帰法を使用して、昨年の指標に基づいて、今年の収益を予測できるかどうかを調べるための関数を作成します。
SELECT *, r_regr_slope(eps, lag_eps) OVER w AS slope_R FROM ( SELECT firm AS f, fyear AS fyr, eps, lag(eps) OVER (PARTITION BY firm ORDER BY firm, fyear) AS lag_eps FROM test_data ) AS a WHERE eps IS NOT NULL WINDOW w AS (PARTITION BY firm ORDER BY firm, fyear ROWS 8 PRECEDING); f | fyr | eps | lag_eps | slope_r
ご覧のとおり、この関数は収入の前年の指標への依存度を計算しました。
最後に詳しく説明するのは、Rオブジェクトを返すためのメカニズムと、それらを保存する方法です。
在庫データの例を示します。 これを行うには、「ティッカー」(株価表示)のYahooからHi-Low-Closeデータを取得します。 ボリンジャーの線とボリュームでチャートを作成しましょう。 次のコマンドを使用してRから取得できる追加のRパケットが必要です。
install.packages(c('xts','Defaults','quantmod','cairoDevice','RGtk2'))
リクエストを行います:
CREATE OR REPLACE FUNCTION plot_stock_data(sym text) RETURNS bytea AS $$ library(quantmod) library(cairoDevice) library(RGtk2) pixmap <- gdkPixmapNew(w=500, h=500, depth=24) asCairoDevice(pixmap) getSymbols(c(sym)) chartSeries(get(sym), name=sym, theme="white", TA="addVo();addBBands();addCCI()") plot_pixbuf <- gdkPixbufGetFromDrawable(NULL, pixmap, pixmap$getColormap(),0, 0, 0, 0, 500, 500) buffer <- gdkPixbufSaveToBufferv(plot_pixbuf, "jpeg", character(0), character(0))$buffer return(buffer) $$ LANGUAGE plr;
一般的なサーバーでは、グラフを作成するために画面バッファーが必要です。
Xvfb :1 -screen 0 1024x768x24 export DISPLAY=:1.0
CYMIティッカーの関数をPHPから呼び出します。
<?php $dbconn = pg_connect("..."); $rs = pg_query($dbconn, "select plr_get_raw(plot_stock_data('CYMI'))"); $hexpic = pg_fetch_array($rs); $cleandata = pg_unescape_bytea($hexpic[0]); header("Content-Type: image/png"); header("Last-Modified: " . date("r", filectime($_SERVER['SCRIPT_FILENAME']))); header("Content-Length: " . strlen($cleandata)); echo $cleandata; ?>
そして、ここで出力でそのようなグラフを取得します:
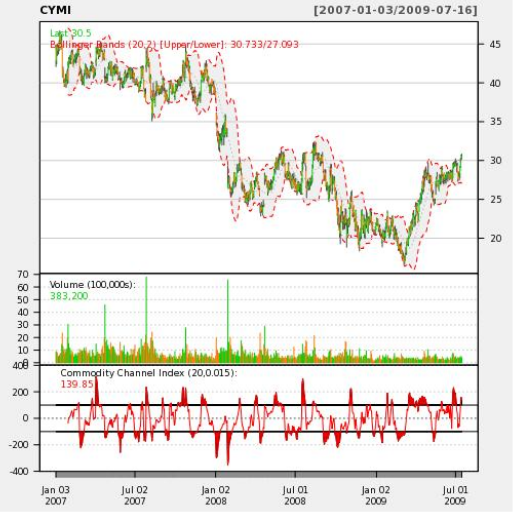
同意します。PL/ Rで数十行、PHPで数十行未満を記述できることは驚くべきことです。その結果、データの詳細な視覚表示と分析が可能になります。
情報を統合するには、より複雑な例を検討してください。 多くの人がベンフォードの法則、または実数から取得した量の分布に特定の最初の重要な数字が現れる確率を記述する最初の数字の法則に精通していると思います。 しかし、その存在を知らず、法律を適用する代わりに、必要に応じてデータを配信する人もいます。
ベンフォードの法則は、潜在的な詐欺の特定に使用できます。その助けを借りて、いくつかの初期値に基づいて近似の幾何学的シーケンスを構築し、それを実際のデータと比較して矛盾を見つけることができます。 この方法は、販売スケジュール、国勢調査データ、コストレポートなどに適用できます。
カリフォルニアのエネルギー効率最適化プログラムの例を考えてみましょう。 まず、プロジェクトへの投資に関するデータを含むテーブルを作成して記入します(データは
http://open-emv.com/dataで入手できます)。
CREATE TABLE open_emv_cost(value float8, district int); COPY open_emv_cost FROM 'open-emv.cost.csv' WITH delimiter ',';
次に、ベンフォードの法則の関数を書きます。
CREATE TYPE benford_t AS ( actual_mean float8, n int, expected_mean float8, distorion float8, z float8 ); CREATE OR REPLACE FUNCTION benford(numarr float8[]) RETURNS benford_t AS $$ xcoll <- function(x) { return ((10 * x) / (10 ^ (trunc(log10(x))))) } numarr <- numarr[numarr >= 10] numarr <- xcoll(numarr) actual_mean <- mean(numarr) n <- length(numarr) expected_mean <- (90 / (n * (10 ^ (1/n) - 1))) distorion <- ((actual_mean - expected_mean) / expected_mean) z <- (distorion / sd(numarr)) retval <- data.frame(actual_mean,n,expected_mean,distorion,z) return(retval) $$ LANGUAGE plr;
そして、比較を実行します。
SELECT * FROM benford(array(SELECT value FROM open_emv_cost)); -[ RECORD 1 ]-+
実際のデータは予測と一致しているようであるため、この場合、不正の兆候はありません。
巡回セールスマンの問題に戻りましょう。 これは組み合わせ最適化の最も有名な問題の1つです。これは、これらの都市を少なくとも1回通過してから元の都市に戻る最も収益性の高いルートを見つけることにあります。 問題の状況では、ルートの収益性の基準(最短、最低、集約基準など)と、距離、コストなどの対応するマトリックスが示されます。 原則として、ルートは各都市を1回だけ通過する必要があることが示されています。 この特定のオプションを見てみましょう。
最初に、訪問する必要があるすべての都市を含むテーブルを作成し、入力します。
CREATE TABLE stands ( id serial primary key, strata integer not null, initage integer ); SELECT AddGeometryColumn('','stands','boundary','4326','MULTIPOLYGON',2); CREATE INDEX "stands_boundary_gist" ON "stands" USING gist ("boundary" gist_geometry_ops); SELECT AddGeometryColumn('','stands','location','4326','POINT',2); CREATE INDEX "stands_location_gist" ON "stands" USING gist ("location" gist_geometry_ops); INSERT INTO stands (id,strata,initage,boundary,location) VALUES ( 1,1,1, GeometryFromText( 'MULTIPOLYGON(((59.250000 65.000000,55.000000 65.000000,55.000000 51.750000, 60.735294 53.470588, 62.875000 57.750000, 59.250000 65.000000 )))', 4326 ), GeometryFromText('POINT( 61.000000 59.000000 )', 4326) ), ( 2,2,1, GeometryFromText( 'MULTIPOLYGON(((67.000000 65.000000,59.250000 65.000000,62.875000 57.750000, 67.000000 60.500000, 67.000000 65.000000 )))', 4326 ), GeometryFromText('POINT( 63.000000 60.000000 )', 4326 ) ), ( 3,3,1, GeometryFromText( 'MULTIPOLYGON(((67.045455 52.681818,60.735294 53.470588,55.000000 51.750000, 55.000000 45.000000, 65.125000 45.000000, 67.045455 52.681818 )))', 4326 ), GeometryFromText('POINT( 64.000000 49.000000 )', 4326 ) ) ;
結果を得るには、いくつかの補助クエリを作成する必要があります。 最初のものは、出力で取得したいルートを作成します:
INSERT INTO stands (id,strata,initage,boundary,location) VALUES ( 4,4,1, GeometryFromText( 'MULTIPOLYGON(((71.500000 53.500000,70.357143 53.785714,67.045455 52.681818, 65.125000 45.000000, 71.500000 45.000000, 71.500000 53.500000 )))', 4326 ), GeometryFromText('POINT( 68.000000 48.000000 )', 4326) ), ( 5,5,1, GeometryFromText( 'MULTIPOLYGON(((69.750000 65.000000,67.000000 65.000000,67.000000 60.500000, 70.357143 53.785714, 71.500000 53.500000, 74.928571 54.642857, 69.750000 65.000000 )))', 4326 ), GeometryFromText('POINT( 71.000000 60.000000 )', 4326) ), ( 6,6,1, GeometryFromText( 'MULTIPOLYGON(((80.000000 65.000000,69.750000 65.000000,74.928571 54.642857, 80.000000 55.423077, 80.000000 65.000000 )))', 4326 ), GeometryFromText('POINT( 73.000000 61.000000 )', 4326) ), ( 7,7,1, GeometryFromText( 'MULTIPOLYGON(((80.000000 55.423077,74.928571 54.642857,71.500000 53.500000, 71.500000 45.000000, 80.000000 45.000000, 80.000000 55.423077 )))', 4326 ), GeometryFromText('POINT( 75.000000 48.000000 )', 4326) ), ( 8,8,1, GeometryFromText( 'MULTIPOLYGON(((67.000000 60.500000,62.875000 57.750000,60.735294 53.470588, 67.045455 52.681818, 70.357143 53.785714, 67.000000 60.500000 )))', 4326 ), GeometryFromText('POINT( 65.000000 57.000000 )', 4326) ) ;
2番目は、plr_modulesに入力するデータと、結果のデータのタイプです。
DROP TABLE IF EXISTS events CASCADE; CREATE TABLE events ( seqid int not null primary key,
メインのPL / R関数を作成します。
CREATE OR REPLACE FUNCTION solve_tsp(makemap bool, mapname text) RETURNS SETOF events AS $$ require(TSP) require(fields) sql.str <- "select id, st_x(location) as x, st_y(location) as y, location from stands;" waypts <- pg.spi.exec(sql.str) dist.matrix <- rdist.earth(waypts[,2:3], R=3949.0) rtsp <- TSP(dist.matrix) soln <- solve_TSP(rtsp) tour <- as.vector(soln) pg.thrownotice( paste("tour.dist=", attributes(soln)$tour_length)) route <- make.route(tour, waypts, dist.matrix) if (makemap) { make.map(tour, waypts, mapname) } return(route) $$ LANGUAGE 'plr' STRICT;
ここで、make.route()関数を設定する必要があります。
INSERT INTO plr_modules VALUES ( 0, $$ make.route <-function(tour, waypts, dist.matrix) { velocity <- 500.0 starts <- tour[1:(length(tour))-1] stops <- tour[2:(length(tour))] dist.vect <- diag( as.matrix( dist.matrix )[starts,stops] ) last.leg <- as.matrix( dist.matrix )[tour[length(tour)],tour[1]] dist.vect <- c(dist.vect, last.leg ) delta.x <- diff( waypts[tour,]$x ) delta.y <- diff( waypts[tour,]$y ) bearings <- atan( delta.x/delta.y ) * 180 / pi bearings <- c(bearings,0) for( i in 1:(length(tour)-1) ) { if( delta.x[i] > 0.0 && delta.y[i] > 0.0 ) bearings[i] <- bearings[i] if( delta.x[i] > 0.0 && delta.y[i] < 0.0 ) bearings[i] <- 180.0 + bearings[i] if( delta.x[i] < 0.0 && delta.y[i] > 0.0 ) bearings[i] <- 360.0 + bearings[i] if( delta.x[i] < 0.0 && delta.y[i] < 0.0 ) bearings[i] <- 180 + bearings[i] } route <- data.frame(seq=1:length(tour), ptid=tour, bearing=bearings, dist.vect=dist.vect, velocity=velocity, travel.time=dist.vect/velocity, loiter.time=0.5) route$total.travel.dist <- cumsum(route$dist.vect) route$total.travel.time <- cumsum(route$travel.time+route$loiter.time) route$location <- waypts[tour,]$location return(route)}$$ );
make.map()関数:
INSERT INTO plr_modules VALUES ( 1, $$make.map <-function(tour, waypts, mapname) { require(maps) jpeg(file=mapname, width = 480, height = 480, pointsize = 10, quality = 75) map('world2', xlim = c(20, 120), ylim=c(20,80) ) map.axes() grid() arrows( waypts[tour[1:(length(tour)-1)],]$x, waypts[tour[1:(length(tour)-1)],]$y, waypts[tour[2:(length(tour))],]$x, waypts[tour[2:(length(tour))],]$y, angle=10, lwd=1, length=.15, col="red" ) points( waypts$x, waypts$y, pch=3, cex=2 ) points( waypts$x, waypts$y, pch=20, cex=0.8 ) text( waypts$x+2, waypts$y+2, as.character( waypts$id ), cex=0.8 ) title( "TSP soln using PL/R" ) dev.off() }$$ );
TSPタグを受信する機能を開始します。
詳細ビュー:
\x SELECT * FROM solve_tsp(true, 'tsp.jpg'); NOTICE: tour.dist= 2804.58129355858 -[ RECORD 1 ]
したがって、これらの都市を訪れる価値がある順序、それらの都市間の距離などを取得しました。 さらに、巡回セールスマンの問題に対する明確な解決策があります。

今度は地震データを使用した別の例を考えてみましょう。
地震が発生すると、通常15〜20秒続き、地震学者はその振動の強度に関するデータを収集します。 つまり、波形の形式のデータの時系列(timeseries)(波形データ)があります。 データは、一定のサンプリング周波数で地震イベント中に記録された浮動小数点数(浮動小数点数)の配列として保存されます。 これらは、各アクティビティの個別のファイルでオンラインソースから入手できます。 各ファイルには約16,000の要素が含まれています。
PL / pgSQLを使用して1000の地震活動をロードします。
DROP TABLE IF EXISTS test_ts; CREATE TABLE test_ts ( dataid bigint NOT NULL PRIMARY KEY, data double precision[] ); CREATE OR REPLACE FUNCTION load_test(int) RETURNS text AS $$ DECLARE i int; arr text; sql text; BEGIN arr := pg_read_file('array-data.csv', 0, 500000); FOR i IN 1..$1 LOOP sql := $i$INSERT INTO test_ts(dataid,data) VALUES ($i$ || i || $i$,'{$i$ || arr || $i$}')$i$; EXECUTE sql; END LOOP; RETURN 'OK'; END; $$ LANGUAGE plpgsql; SELECT load_test(1000); load_test
これは、Rの助けを借りて別の方法で行うことができ、半分の時間がかかります-PL / Rを使用する場合、プロセスを遅くするのではなく、スピードアップすることはまれです:
DROP TABLE IF EXISTS test_ts_obj; CREATE TABLE test_ts_obj ( dataid serial PRIMARY KEY, data bytea ); CREATE OR REPLACE FUNCTION make_r_object(fname text) RETURNS bytea AS $$ myvar<-scan(fname,sep=",") return(myvar); $$ LANGUAGE 'plr' IMMUTABLE; INSERT INTO test_ts_obj (data) SELECT make_r_object('array-data.csv') FROM generate_series(1,1000); INSERT 0 1000 Time: 12166.137 ms
オシログラムを作成しましょう:
CREATE OR REPLACE FUNCTION plot_ts(ts double precision[]) RETURNS bytea AS $$ library(quantmod) library(cairoDevice) library(RGtk2) pixmap <- gdkPixmapNew(w=500, h=500, depth=24) asCairoDevice(pixmap) plot(ts,type="l") plot_pixbuf <- gdkPixbufGetFromDrawable( NULL, pixmap, pixmap$getColormap(), 0, 0, 0, 0, 500, 500 ) buffer <- gdkPixbufSaveToBufferv( plot_pixbuf, "jpeg", character(0), character(0) )$buffer return(buffer) $$ LANGUAGE 'plr' IMMUTABLE; SELECT plr_get_raw(plot_ts(data)) FROM test_ts WHERE dataid = 42;
特定の地震についてこの画像を取得します。

次に、たとえば、同様の地震活動がある地域で建物を設計する最善の方法を見つけるために、分析する必要があります。 おそらく、学校の物理学コースで「共振周波数」などのことを覚えているでしょう。 念のため、これは発振振幅が急激に増加するような発振周波数であることを思い出させてください。 この頻度は、システムのプロパティによって決まります。 つまり、地震活動のある地域では、共振周波数が地震の周波数と一致しないように構造を設計する必要があります。 これはRを使用して実行できます。
CREATE OR REPLACE FUNCTION plot_fftps(ts bytea) RETURNS bytea AS $$ library(quantmod) library(cairoDevice) library(RGtk2) fourier<-fft(ts) magnitude<-Mod(fourier) y2 <- magnitude[1:(length(magnitude)/10)] x2 <- 1:length(y2)/length(magnitude) mydf <- data.frame(x2,y2) pixmap <- gdkPixmapNew(w=500, h=500, depth=24) asCairoDevice(pixmap) plot(mydf,type="l") plot_pixbuf <- gdkPixbufGetFromDrawable( NULL, pixmap, pixmap$getColormap(), 0, 0, 0, 0, 500, 500 ) buffer <- gdkPixbufSaveToBufferv( plot_pixbuf, "jpeg", character(0), character(0) )$buffer return(buffer) $$ LANGUAGE 'plr' IMMUTABLE; SELECT plr_get_raw(plot_fftps(data)) FROM test_ts_obj WHERE dataid = 42;
そして、これは最終結果がどのように見えるかであり、振動の周波数とその振幅を示しています:

建築家はこのようなスケジュールを目の前にして、計算を行い、最初の震えで崩壊しない構造を設計できます。
ご覧のように、PL / Rにはアプリケーションの多くの領域があります。高度な分析をデータベースに接続し、同時にRとPostgreSQLの機能をすべての利点とともに使用できるためです。 この記事がお役に立てば幸いです。そして、このような効果的で汎用性の高いツールの使用を見つけてください。
また、この記事が作成された資料に基づいて、PG Day'15 RussiaでのJoe Conwayのパフォーマンスからのプレゼンテーションとビデオをご覧ください。 PL / Rを使用するトピックがあなたにとって興味深いと思われる場合は、必ずあなたの考えやアイデアを共有してください。 7月に開催されるPG Day'16で、このトピックに関するレポートを整理するかもしれません。 いつものように、あなたのコメントを待っています。