Pythonと美脚：息子を数学とプログラミングに紹介する方法

Python Scikit-learnライブラリを使用して、珍しいプレイボーイモデルを探していました 。 ここで、SymPy、SciPy、Matplotlib、およびPandasライブラリの機能の一部を、楽しい学校の数学の問題のカテゴリからの実例を使用して示します。 目標は、データ分析用のPythonライブラリを学習する際にエントリのしきい値を緩和することです。

タスク1

優雅で、訓練された、そして最も重要な裸足の少女がいます。 あなたがいなくて寂しいです。 ピックアップテクノロジーの（n + 1）番目のレベルを実証する前に、女の子の足をよりよく調べたいと思います。 検討するのが良い-これは最大の角度です。 静かに女の子に近づくことができます（遠くを見ているように見えます）が、しゃがむことはできません-なんとなく品位を尊重しなければなりません。 脚はどの角度から最大の角度で見えますか？ あなたの目が地球の表面からmの高さにあると仮定します。 女の子の足はfの高さまで裸です。

解決策

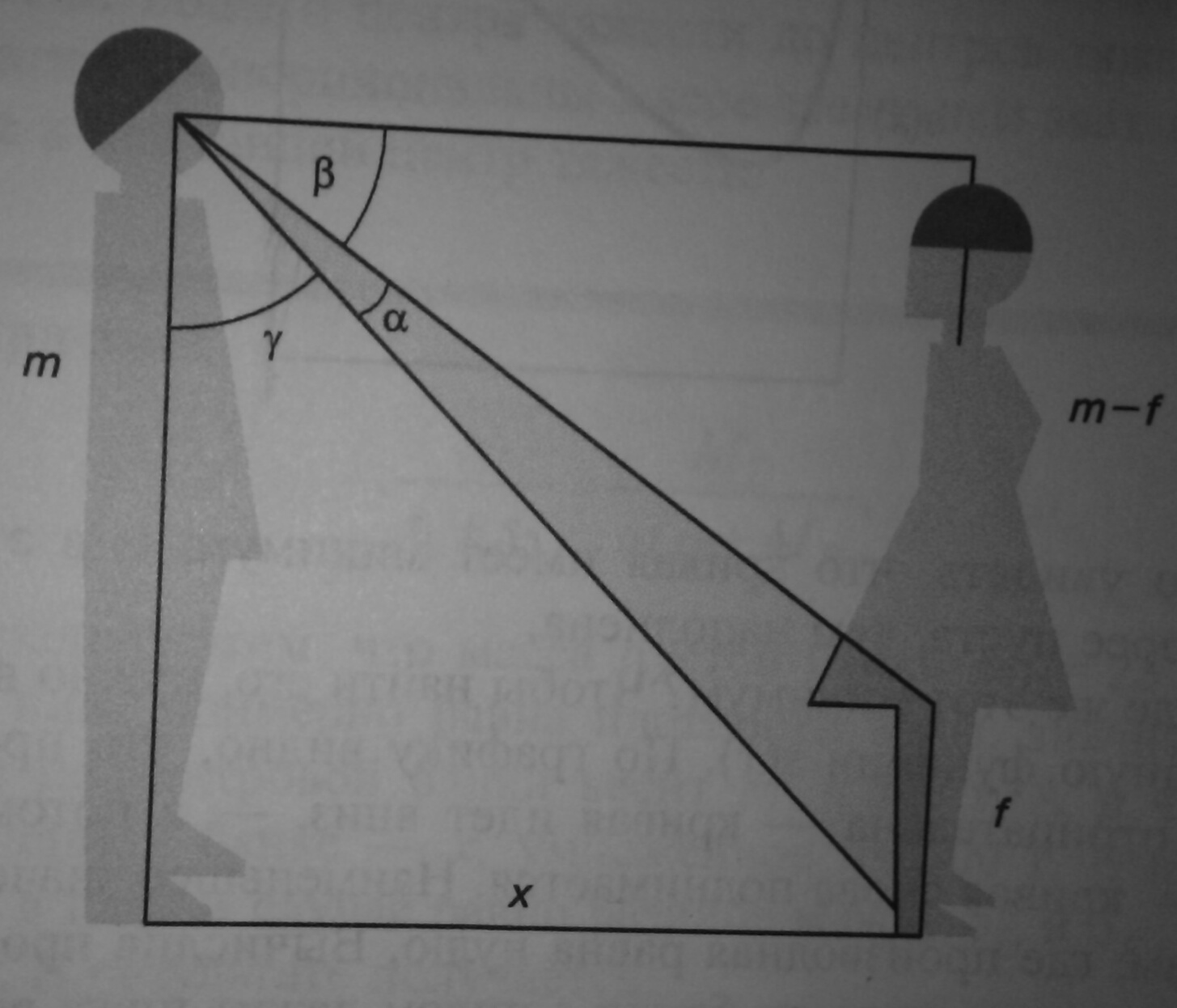
「クリストフドレッサー：数学の誘惑」の画像と言い換えタスク。 すべての機会のための数値ゲーム。 ビノム。 ナレッジラボ、2015年

問題を説明しましょう。 遠くから見ると、足を見るのは良くありません-あまりにも小さな角度で見えます。 しかし、近づきすぎても、脚は小さな角度で見えます。 どこかに最適な距離があるはずです。

xを少女までの距離、fを少女の脚の裸の部分の長さ、alphaを脚が見える角度とします（最大化する必要があります）。

アルファ角は、直角からベータ角とガンマ角を引くことで最も簡単に見つけることができます。 学校の三角法が脳の裏通りでまだ何らかの形で生きている場合、私たちは簡単にそれを取得します



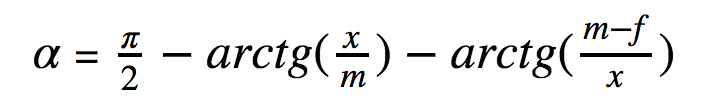
この問題は、変数xに関してアルファ（x）を最大化することにつながります。
まあ、それも簡単です、私たちは言います：派生物を無効にして-行ってください！

最初に、関数alpha（x）をプロットします。 明確にするために、パラメータm = 1.7 mおよびf = 0.7 mの値を使用します（1 mが必要ですが、特定のスカートがあると仮定されます）。

これでコード。 AnacondaアセンブリとIPythonノートブックが使用されます。 コードは再現可能で、 GitHub リポジトリにあります 。

#    Anaconda import warnings warnings.filterwarnings('ignore') #   IPython,       %pylab inline import numpy as np from math import pi, atan 

 def alpha(x, m, f): return pi/2 - atan(x/m) - atan((mf)/x) #       x = np.arange(0, 6, 0.05) plot(x, [alpha(i, 1.7, 0.7) for i in x]) 

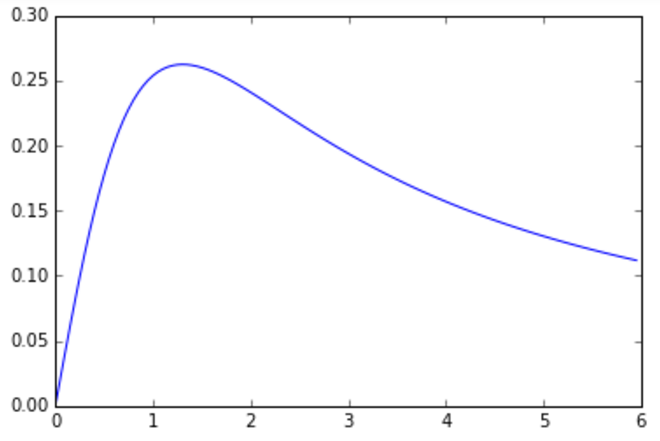
ああ！ 仮定が確認されました：少女から1〜1.5mのどこかで、彼女の足は最大の角度で見えます。 まあ...それは青白いせずにすでに困難です。 次に、女の子までの最適な距離の正確な値を見つけましょう。

「手作業」による分析ソリューション

解析ソリューションは非常にシンプルで、アークタンジェントの導関数を覚えておいてください。 LaTeXはHabréではサポートされていないため、この部分は対応するIPythonノートブックにあります。
結果は次のとおりです。

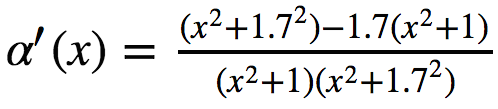
SymPyによる分析ソリューション

SymPyはPythonシンボルライブラリです。 微分を計算する方法（diffメソッド）と方程式の根を見つける方法（solveメソッド）を検討します。

 import sympy as sym 

シンボル変数xと関数alpha（x）を取得します。 シンボリック計算の場合、Pi番号とアークタンジェントもSymPyから取得する必要があります。

 x = sym.Symbol('x') alpha = sym.pi/2 - sym.atan(x/1.7) - sym.atan(1/x) 

 alpha # -atan(1/x) - atan(0.588235294117647*x) + pi/2 

導関数alpha '（x）を計算します。 diffメソッドは、関数、微分が発生する変数、および導関数の順序（この場合は1）を指定する必要があります。

 alpha_deriv = sym.diff(alpha, x, 1) 

 alpha_deriv # -0.59/(0.35*x**2 + 1) + 1/(x**2*(1 + x**(-2))) 

これは、鉛筆と紙を手に取った場合と同じことを確認できます。

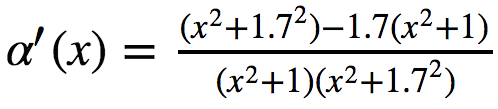
ご覧のとおり、SymPyの共通分母は単に表現につながりません。 これには簡単な方法があります。

 sym.simplify(alpha_deriv) # (-0.24*x**2 + 0.41)/((0.35*x**2 + 1)*(x**2 + 1)) 

次に、解法を使用して導関数のゼロを見つけます。

 sym.solve(alpha_deriv, x) # [-1.30384048104053, 1.30384048104053] 

ここでも、約1.3 mの女の子を考慮するのが最善であることがわかりました。興味深いことに、写真家もそのような計算を実行しますか？

SciPy数値解

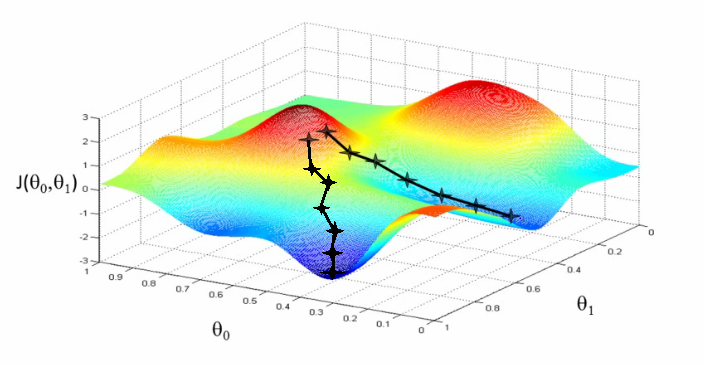Andrew Ng機械学習コースの画像

SciPyライブラリでは、有用なすべてに加えて、数値最適化のさまざまな方法が実装されています。 1次元および多次元関数を最小化するための多くの方法の詳細な説明は、scipy.optimize.minimizeメソッドのドキュメントに記載されています 。

そのような最大化方法はないため、関数時間を最小化することで最大化の問題をエミュレートします（-1）。 最も単純な場合、つまり1つの変数のスカラー関数を最小化することを検討してください。 「ブレント」、「境界」、および「ゴールデン」の最適化方法が実装されていますが 、何らかの理由で違いが明確に文書化されていません 。

 from scipy.optimize import minimize_scalar alpha = lambda x: -(pi/2 - atan(x/1.7) - atan(1/x)) result = minimize_scalar(alpha, bounds=[0., 100.], method = 'bounded') 

答えは予想と同じです。

 result.x # 1.3038404104038319 

今、私たちが賞賛する足を持つ少女を選んでください。 今月のPlayboyモデルの使い慣れたgirls.csvデータセットに戻ります。 最高の非栄養障害の女の子を選択してください。 同時に、Pandasライブラリから何かを紹介します。

タスク2

プレイボーイモデルの中で、「正常な」ボディマスインデックスが18から18.5までの最も成長の大きい女の子を見つけます。

解決策

 import pandas as pd girls = pd.read_csv('girls.csv') #  Pandas.DataFrame girls.head() #  5   

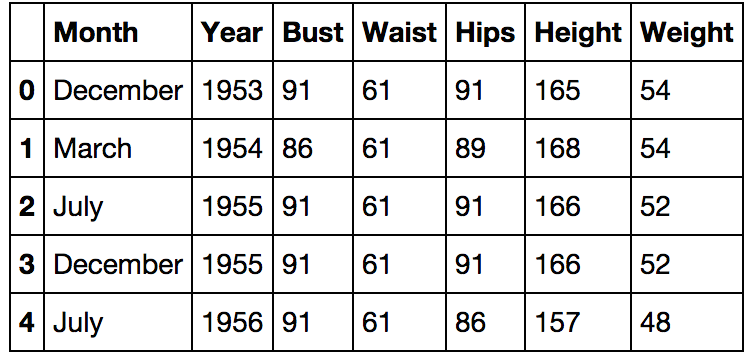
新しいBMI機能を作成しましょう-体重を2乗単位の身長で割った体重に等しいボディマスインデックス 。

 girls['BMI'] = 100 ** 2 * girls['Weight'] / (girls['Height'] ** 2) 

BMI分布のヒストグラムをプロットします。

 girls['BMI'].hist() 

ウィキペディアによると、通常のBMIは18.5-24.99です。 Playboyモデルの平均インデックスは、ほぼ標準の下限にあることがわかります。
18から18.5までのBMIを持つ少女を選択します。

 selected_girls = girls[(girls['BMI'] >= 18) & (girls['BMI'] <= 18.5)] 

 selected_girls.sort(columns=['Height', 'Bust'], ascending=[False, False]).head(1) # Month Year Bust Waist Hips Height Weight BMI #430 July 1994 91 61 91 180 59 18.209877 

これはPlayboy Traci Adellによる1994年7月のミスです。 さらなる検索エンジン。 そのような選択は失望することはないでしょう。

そこで、PythonライブラリSymPy、SciPy、およびPandasを使用する非常に基本的なことを検討しました。 これらのライブラリの実際の使用例は、GitHubリポジトリに豊富にあります。 このようなリポジトリのレビューの1つはこちらです。