このホワイトペーパーでは、便利な表記法から特別な信頼性の見積もりまで、小さなサンプルでのトレーニングによる分類の概要を説明します。 コンピューティングデバイスと小さなサンプルの速度が絶えず増加しているため、これらの推定値の一部を取得するために必要な大量の計算を無視することができます。
定義と表記
セットの初期パーティションを指定します
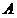
オブジェクト
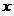
2つのサブセット(クラス)に
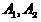
そのような
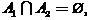
、
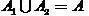
。
(1)
次の形式のバイナリ関数を使用して、2クラス分類器を識別します。
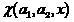
(2)
どこで
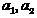
-ランダムなサブセット
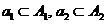
クラスから
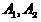
、
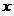
-調査対象オブジェクト。クラスのいずれかに帰属する必要があります。 この関数の値は、ルールに従って「決定」として解釈されます
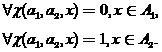
(3)
分類器ソリューションが元のパーティションに対応するかどうかに応じて
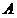
クラスに分類する場合、それぞれを「正しい」または「間違っている」と見なします。 私たちも同意します
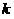
サンプリング要素
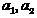
意味する

、したがって、それぞれ:
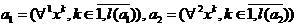
、
(4)
どこで
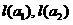
-トレーニングサンプルの量。 私たちはたくさん信じています
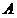
没入
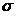
次元右ユークリッド空間
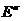
。 次に、クラスのすべての要素
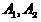
もちろん、トレーニングサンプルの要素と調査対象のオブジェクトの両方をそのポイントと見なすことができます。 セットの点オブジェクトの座標
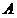
右下のインデックスでマークされます
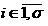
。 オブジェクト座標
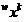
トレーニングサンプルは次のように記述されます。
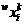
調査対象の
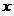
方法-
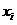
。 コンテキストに応じて、
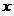
オブジェクトの名前、または半径ベクトルとして理解されます。
検証シーケンスがないことから進み、分類エラーの確率の推定
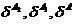
ローリング試験モードで実行可能
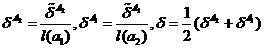
、
(5)
どこで
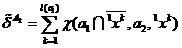
、
(6)
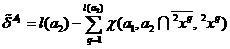
。
(7)
オブジェクト
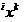
スライディング試験モードで分類されたトレーニングサンプルは、今後準試験可能と呼ばれます。
調整済みの移動試験
ご存知のように、スライド式試験には多くの欠点があります。 これらの欠点は、スライド式試験を修正することである程度解消できます。 左調整調整グレードは次のように記述されます
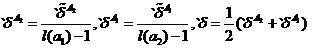
、
(8)
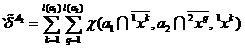
、
(9)
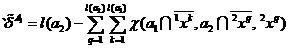
。
(10)
調整されたローリング試験の欠点には、操作数の増加と、この評価がより小さなボリュームの単位ごとに両方のサンプルで実行されるという事実が含まれます。 したがって、小さなサンプルの場合、エラーの確率の推定値はやや過大評価されますが、サンプルサイズが大きくなると、この効果は価値を失います。
分類子
調整された移動試験は非常に複雑であるため、分類の信頼性のバイナリ評価の方法-共同分類子-が重要です。 移動試験のように、トレーニングサンプルからの情報のみに基づくことができますが、テストシーケンスが存在する場合にも使用できます。
サンプルを紹介します
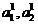
スライド検査モードで分類器(2)によってそれぞれ正しく、誤って割り当てられたオブジェクト
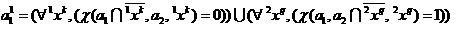
、
(11)

。
(12)
次に、分類器(2)の1次の共分類器の解は、次のように定義されます。
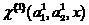
、
(13)
次のように解釈されます
もし
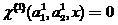
次に、分類子(2)は、
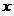
、
もし
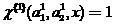
その後、分類器(2)は、
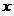
。
(14)
さらに、サンプルが
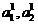
いくつかのクラスから抽出
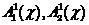
分類子によって潜在的に正しくまたは誤って割り当てられたオブジェクト(2)。
(13)を決定する際、サンプルサイズは
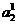
小さすぎません。 したがって、トレーニングサンプルの資料のみがあり、検証シーケンスがない場合、分類子(2)がかなりの数のエラーを起こす条件で共分類子を使用することをお勧めします。 まだ小さなサンプルで共分類器を使用している場合
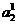
、それからかなり単純な形式で選択する必要があります。 たとえば、共分類器がフィッシャー型である場合、共分散行列の対角性またはその同一性さえも想定できます。
適応ブースティングのように、分類器の構成
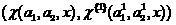
は、[1]で提案されたものよりも実質的に非線形に組織化された集合分類器と見なすことができます。
共分類子の特定の形式の選択に関連する問題について説明します。 たとえば、サンプル
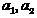
クラスから抽出
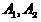
分布密度
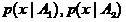
、およびクラスは大きく重複しています。 この場合、サンプル密度が
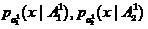
平均値が近い。 この場合、分類子
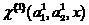
たとえば、Peterson – Mattsonの手順[2,3]を使用して修正された線形Fisher分類器の形式で選択できます。
フラクタル分類器
置換が最初に実行されるとき、高次の共分類子の合成は、再帰手順の一部として継続できます。
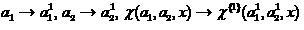
、
(15)
次に、上記のアルゴリズムを繰り返して、2次共分類子を取得します
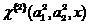
。
(16)
この手順を続けます。 この順序の共分類子を構築すると、強制停止が発生します

どこで
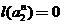
または
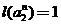
。 結果として、分類器の反復システム、つまりフラクタル分類器を取得します。 もちろん、この集合分類器を、フラクタル変換とウェーブレット変換を使用して処理する画像分類器と混同しないでください。
実際には、ファーストクラスの共分類子のみを使用する必要がありました。 彼らは何年も前に私たちによって開発され、特にプラスチック製対人地雷[4]の捜索設備の反射無線信号の分析やLEKTONシステムの作成において、さまざまな実際的な問題を解決するための有用なツールとして確立されました。 このシステムにより、小切手、請求書、その他の書類の署名の真正性を自動的に検証することが可能になり、銀行で実際に使用されたこのタイプの最初のシステムとなりました。
ローカルエラー確率
実際の研究では、ローカル
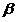
-分類エラーの確率の推定。 分類子(2)を次の形式で表すことができます
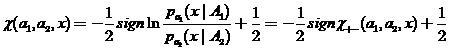
、
(17)
どこで
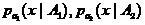
-密度推定
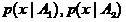
サンプルごと
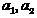
それに応じて。 それからローカル
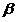
-この分類器のエラーの確率の推定値は、次のように定義できます。
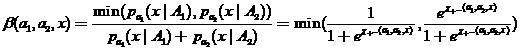
、
(18)
どこで
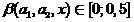
。
スペシャルを紹介します

-「ファジー」分類子と見なすことができる評価
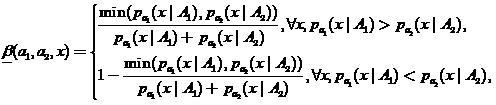
(19)
どこで
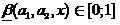
。 次に、
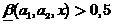
ファジー分類器の解として解釈される
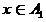
、
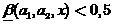
-その決定として
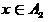
。 また、近い
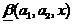
ゼロまたは統一まで、曖昧な分類器の対応するソリューションはより信頼できます。
評価(19)に基づいて、分類器(2)の定義は、障害ゾーンまたは障害ゾーンを導入することで一般化できます。 これらのゾーンの幅をそれぞれ示す
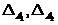
、それらを次の形式で想像してください
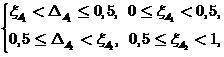
(20)
どこで
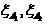
-ゾーンの境界。 ゾーンの要件に非対称性がない場合は、選択します
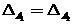
。
参照:
1. Archipov GF決定的ルールの集合体:最適なソリューションと分類の信頼性の特徴。 -記事集「制御の統計的問題」、ビリニュス、1983、vol。61、pp。 130-145。
2. Myasnikov VV Peterson-Mattson手続きに基づく線形判別関数の構築方法の修正について。 computeroptics.smr.ru/KO/PDF/KO26/KO26211.pdf。
3.福永K.パターン認識の統計理論入門。 M. "Science" 1979. p。105-130。
4. Archipov G.、Klyshko G.、Stasaitis D.、Levitas B.、Alenkowicz H.、Jefremov S.反射された無線信号の元のコンピューター認識技術に基づいた金属および誘電体の地下物体の研究。 MIKON-2000。、XII International Conference on Microwaves、Radar and Wireless Communications、Volume 2、pp。 495-498 ./>