普遍的なレーベンシュタインオートマトンを使用した辞書でのファジー検索。 パート2

記事の最初の部分では 、普遍的なレーベンシュタインオートマトンを調べました。これは、ある単語Wから与えられたレーベンシュタイン距離以下の単語をフィルタリングするための強力なツールです。 次は、このツールを使用して、辞書のファジー検索の問題を効果的に解決する方法を学習します。



レーベンシュタインオートマトンを使用して辞書のファジー検索問題を解決するための最も簡単で明白なアルゴリズムは、網羅的な検索アルゴリズムです。 この場合、辞書の各単語について、検索クエリまでのレーベンシュタイン（Damerau-Levenshtein）の距離が推定されます。 C＃の実装例は、記事の最初の部分に記載されています。

この単純なアルゴリズムでさえ、動的プログラミング手法を使用する場合と比較して生産性が向上します。 ただし、より効率的なアルゴリズムがあります。

シュルツとミホフの基本アルゴリズム

最初のそのようなアルゴリズムを考えてみてください-私の知る限り、 Schultz and Mikhov（2002）によって提案されたので、基本的なSchultz and Mikhov アルゴリズムまたは単に基本的なアルゴリズムと呼びます 。 したがって、確定したレーベンシュタインオートマトンA _N （W）が、歪んだと思われる単語Wと編集距離のしきい値_Nに対して与えられるとします。 検討中の辞書Dも、入力アルファベットEを持つ決定論的有限オートマトンA _Dとして表されます。 オートマトンの状態をそれぞれqおよびq ^Dで 、遷移関数をVおよびV ^Dで 、最終状態のセットをFおよびF ^{Dで示します。} SchultzとMihovによって提案された辞書のファジー検索のアルゴリズムは、リターンを伴う標準の検索手順であり 、次の擬似コードで記述できます。



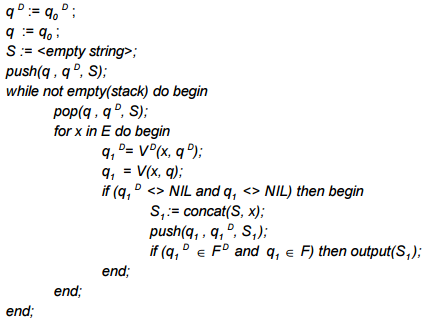
アルゴリズムは、オートマトンの初期状態で動作を開始します。 新しい文字が入力に送られると、後続の状態が空でない場合、スタックにプッシュされます。 両方のオートマトンの次の状態が有限である場合、検索ワードが見つかります。

このアルゴリズムは、有限状態マシンの「交差点」と考えることもできます。 両方のオートマトンの最終状態に対応する単語のみが、結果のサンプルに分類されます。 この場合、両方のマシンを空でない状態に変換するプレフィックスのみが考慮されます。

アルゴリズムの計算の複雑さは、辞書のサイズと編集距離Nに依存します。 Nが辞書内の最長単語のサイズに達すると、アルゴリズムはオートマトンA _Dの状態の完全な列挙になります_。 しかし、実際の問題を解決するときは、原則として、小さな値のNが使用されます。 この場合、アルゴリズムはオートマトンA _Dの状態の非常に小さなサブセットのみを考慮します_。 N = 0の場合、アルゴリズムは時間O（| W |）の辞書で単語Wを見つけます。

説明したアルゴリズムは、検索中に損失がないことを保証することに注意する必要があります。 つまり、 N以内の距離でWから分離されている辞書の単語の100％は、結果のサンプルに分類されます。

ソフトウェア実装の機能

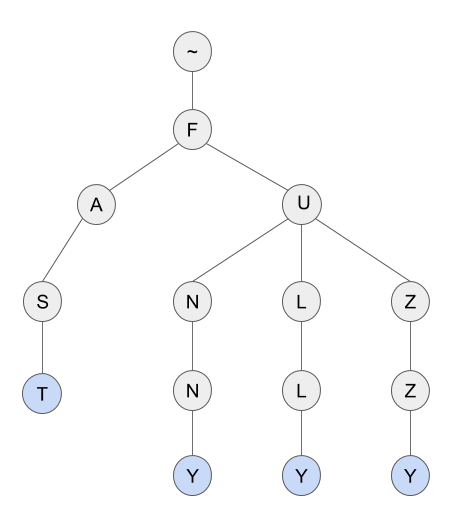
プレフィックスツリーなどのデータ構造に既に精通していると思います。 プレフィックスツリーは、「ロードされたツリー」（または「ホウ素」、「ビーム」、「トライ」）とも呼ばれ、辞書の保存に使用されます。 この図は、「高速」、「面白い」、「完全に」、「ファジー」の4つの単語の辞書のプレフィックスツリーを示しています。



プレフィックスツリーに精通していない場合は、この構造が詳細に説明されている出版物（たとえば、 こちら）に慣れることができます 。

辞書を保存するためにプレフィックスツリーを使用したいのはなぜですか？ プレフィックスツリーは有限状態マシンと見なすことができるためです。 ツリーの各ノードは、オートマトンの状態を表します。 初期状態はツリーのルートであり、最終状態は単語に対応するノードです。 各ノードとシンボルに対して、遷移は1つだけ可能です-オートマトンは決定論的です。

そのため、プレフィックスツリーを決定論的な有限状態マシンと見なし、決定論的なレーベンシュタインオートマトンのソフトウェア実装を持つことを考慮すると、アルゴリズムの擬似コードをプログラミング言語のコードに変えることは難しくありません。 C＃のネタバレの例

FB-Trieアルゴリズム

どうぞ 2004 年、MikhovとSchulzは、上記のアルゴリズムの修正を提案しました。その主なアイデアは、検索クエリWを2つのほぼ等しい部分W ₁とW _2に分割することと組み合わせて、フォワードおよびリバースプレフィックスツリーを使用することです。 このアルゴリズムはFB-Trie（前方および後方トライから）として知られています。

逆プレフィックスツリーは、辞書内のすべての単語の反転から構築されたプレフィックスツリーとして理解する必要があります。 単語の反転、私は単に後方に書かれた単語を意味します。

重要な点-ミホフとシュルツは彼らの研究において、2本の線の反転間のDamerau-Levenshtein距離が線自体の距離に等しいことを示しました。

N = 1のアルゴリズムの動作は、次のステートメントに基づいています。Damerau-Levenshtein距離d（S、W）<= 1だけラインWから離れているラインSは、 S ₁とS _2の2つの部分に分割できます。相互に排他的な3つの条件のいずれか：

a）d（S ₁ 、W ₁ ）= 0およびd（S ₂ 、W ₂ ）<= 1



b）d（S ₁ 、W ₁ ）<= 1およびd（S ₂ 、W ₂ ）= 0



c）d（S ₁ 、W ₁ '）= 0およびd（S ₂ 、W ₂ '）= 0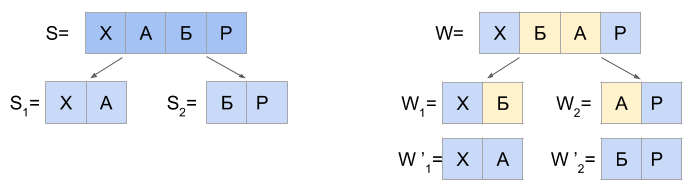



「c」段落では、行W ₁ 'とW ₂ 'は、行W ₁とW ₂から、最後の文字W ₁を最初の文字W _2に 、またはその逆に置き換えることによって取得されます。 たとえば、 W ₁ = 'FU'およびW ₂ = 'ZZY'の場合、 W ₁ ' =' FZ 'およびW ₂ ' = 'UZY'です。

オプション「a」に適合するすべての単語を辞書ですばやく見つけるにはどうすればよいですか？ これは非常に簡単です。プレフィックスツリーでプレフィックスW _1を持つノードを見つけ、基本的なSchultz and Mihovアルゴリズムに従ってそのすべての相続人をバイパスし、 W ₂からキーが1以下のものを選択します。



オプション「b」の場合、逆接頭辞ツリーが便利です。逆行W ₂に対応するノードを見つけ、そのすべての相続人をバイパスし、逆W 1からキーが1以下であるものを選択します-基本アルゴリズムに従って。



オプション「c」の場合、パーティション境界上の単語Wの 2文字を交換し、結果の単語がプレフィックスツリーに含まれているかどうかを確認するだけです。



FB-Trieアルゴリズムを使用してディクショナリのファジー検索の問題を解決するには、上記の3つの単語セットを見つけてそれらを結合するだけです。

N = 2の場合、さらに2つのケースを考慮する必要があります。

a）d（S ₁ 、W ₁ ）= 0およびd（S ₂ 、W ₂ ）<= 2



b）1 <= d（S ₁ 、W ₁ ）<= 2およびd（S ₂ 、W ₂ ）= 0



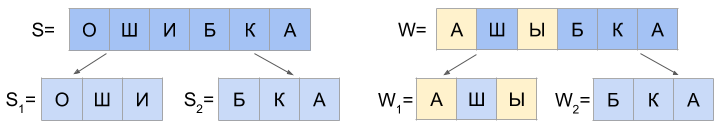c）d（S ₁ 、W ₁ ）= 1およびd（S ₂ 、W ₂ ）= 1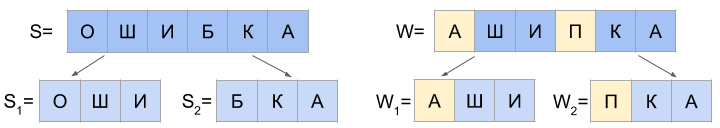



また、文字列S ₁の最後の文字がW _2の最初の文字に等しく、 W _1の最後の文字がS _2の最初の文字に等しい場合、さらに2つのケースが考えられます。

d）d（S ₁ 、W ₁ '）= 0およびd（S ₂ 、W ₂ '）<= 1



d）d（S ₁ 、W ₁ '）<= 1およびd（S ₂ 、W ₂ '）= 0



最初の2つのケースは、 N = 1のオプション「a」と「b」の類推によって簡単に検出されますが、 N = 2のレーベンシュタインオートマトンが使用されます。

N = 2のオプション「g」と「d」は、 N = 1のオプション「a」と「b」を繰り返します。部分文字列W ₁とW _2の代わりに、 W ₁ 'とW ₁ 'が使用されます。

オプション「c」はもう少し複雑です。 最初のステップでは、 W 1（基本アルゴリズム）から1以下のプレフィックスに対応するすべてのノードを直接プレフィックスツリーで見つける必要があります。 2番目のステップでは、そのようなノードごとに、子会社をバイパスし、 W ₂から1以下の間隔のキーに対応する子会社を選択する必要があります（再び、基本アルゴリズム）。

N = 3の場合、7つのケースを考慮する必要があります。 ここでは紹介しません。Mikhovand Schulz（2004）のオリジナル記事をご覧ください。 類推により、任意のNについて続行できますが、実際的な問題を解決する際にこれが必要になることはほとんどありません。

性能評価

興味深いことに、FB-Trieアルゴリズムを使用した検索時間は、語長Wが増加するにつれて減少します。

他の広く知られているファジー検索アルゴリズムと比較したFB-Trieアルゴリズムを使用した検索時間の詳細な分析は、Leonid Boytsovの研究「近似辞書検索のための索引付け方法：比較分析」（2011）にあります。 この作業により、次のようなアルゴリズムで検索時間と消費されるメモリ量を徹底的に比較できます。

• 徹底的な検索。
• n-gramメソッドのさまざまな変更。
• サンプリング拡張メソッドのさまざまな変更。
• 署名ハッシュ
• FB-Trieおよびその他のアルゴリズム。

ここで多数の数字とグラフをすべて繰り返すのではなく、自然言語の一般的な結論に限定します。

そのため、FB-Trieアルゴリズムは、パフォーマンスとメモリ消費の合理的な妥協点を提供します。 アプリケーションが2以上の編集距離を維持する必要があり、辞書に500,000以上の単語が含まれている場合-FB-Trieアルゴリズムは合理的な選択です。 合理的なメモリ消費で最小検索時間を提供します（レキシコンが使用するメモリの約300％）。

編集距離をN = 1に制限する場合、または小さな辞書がある場合は、多くのアルゴリズムがより高速に動作する可能性があります（たとえば、Mor-FraenkelメソッドまたはFastSS ）が、メモリ消費の増加（レキシコンサイズの最大20,000％）に備えてください。 ファジーインデックスを保存するために数十ギガバイトのRAMがある場合、これらのメソッドを大きな辞書サイズで使用できます。

読者がこれがどれだけであるかを決めることができるように-500,000単語、ロシア語の単語数（ ここから引用 ）についていくつかの数字を示します。

1. Lopatinのスペル辞書には162,240語が含まれています。レキシコンファイルのサイズは2 MBです。
2. ロシア語の姓のリストには、少なくとも247,780の姓が含まれています。レキシコンファイルのサイズは4.6 MBです。
3. A. A. Zaliznyakによるロシア語の完全に強調されたパラダイムは、2,645,347の単語形式であり、レキシコンのファイルサイズは約35 MBです。

しかし、2つのプレフィックスツリーの形式で辞書を保存する機能がない場合はどうでしょうか。 たとえば、ソートされたリストとして表示されます。 この場合、ファジー検索にレーベンシュタインオートマトンを使用することは可能ですが、実用的ではありません。 おそらく-徹底的な検索のさまざまな変更が残っているためです（たとえば、単語の長さに沿ったクリッピング| W | plus minus N ）。 実装がより簡単な方法（ サンプル拡張アルゴリズムなど ）と比較してパフォーマンスが向上しないため、実用的ではありません。

基本的なSchultz and Mihovアルゴリズムは、FB-Trieアルゴリズムよりも2倍少ないメモリしか必要としないことに注意してください。 ただし、検索時間を1桁増やすことで、この費用を支払う必要があります（アルゴリズムの作成者の評価）。

これについては、完全なLevenshteinオートマトンを使用した辞書内のファジー検索アルゴリズムの検討を検討します。

はい、C＃のSpellcheckerの完全なソースコードはこちらにあります 。 おそらく私の実装はパフォーマンスの点では最適ではありませんが、FB-Trieアルゴリズムの動作を理解するのに役立ち、アプリケーションの問題を解決するのに役立つかもしれません。

出版物を読んだすべての人に-あなたの興味に感謝します。

参照資料

1. 私の投稿の最初の部分
2. レーベンシュタインオートマトンとシュルツとミホフの基本アルゴリズム（2002）
3. 検索を返す
4. Mihov and Schulzによる記事のFB-Trieアルゴリズム（2004）
5. ファジィ検索専用のLeonid Boytsovのサイト
6. 辞書とテキストのあいまい検索に関する良い投稿
7. プレフィックスツリーについてHabréに投稿する
8. FastSSアルゴリズム
9. C＃の記事のソース
10. Javaでの実装： 1と2
11. ロシア語辞書のセット