この記事は、約1年前にSemenovVVによって公開された「 非再帰的順列生成アルゴリズム 」とテーマが似ているとすぐに言いますが、ここでのアプローチは基本的に異なります。n個の要素のすべての順列のリストをコンパイルする必要に直面しました。
n = 4または5の場合、問題は数分で手動で解決されますが、6の場合です! = 720以上、私はすでにページを書くのが面倒でした-自動化が必要でした。 この「自転車」はすでに何度もさまざまなバリエーションで発明されていると確信していましたが、自分でそれを理解するのは興味深いことでした。したがって、関連する文献を見ずに意図的にアルゴリズムを作成しました。
再帰コードの最初のバージョンは、あまりにも些細でリソース集約的であるとして拒否しました。 さらに、彼は「耳を傾ける」ことで、あまり効率的ではないアルゴリズムを開発し、意図的に多数のオプションを選別し、適切なオプションのみを除外しました。 それは機能しましたが、エレガントなものが欲しかったため、ゼロから始めて、
nの小さな値の辞書順の順序でパターンを探し始めました。 結果は、最小限の「結び付け」でPythonで10行で表すことができるきちんとしたコードになりました(以下を参照)。 さらに、このアプローチは順列だけでなく、
n個の要素を
m個の位置に配置する場合にも機能します(n≥mの場合)。
4〜4のすべての順列のリストを見ると、特定の構造が顕著です。
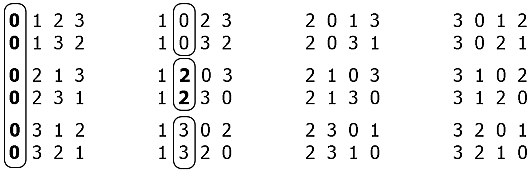
順列の配列全体(4!= 24)は
(n-1)!のグループに分割できます
! = 3! -6つの順列、そして各グループは順番に
(n-1-1)に分割され
ます! = 2! –2つの組み合わせなど。 考慮されるケースでは、
n = 4の場合、それがすべてです。
したがって、辞書編集の観点からは、この順列のセットは増加するシリーズと考えることができます:0123 <0132 <... <3210、いわば。特定の位置で同じ要素が何回繰り返されるかを事前に知っています-これは配列の順列の数です1つ少ない注文、つまり
(a-1)! ここで
、aは現在の配列の次元です。 次に、次の値への遷移の符号は、組み合わせのシーケンス番号
iをそのような順列の数で整数除算( "
// ")した新しい結果になります
。i //(a-1)! 。 また、この要素の数が未使用のリストにあるかどうかを判断するには(円で繰り返さないように)、取得した値をこのリストの長さで割った余り(「
% 」)を使用します。 T.O. 次の構造があります。
i //(a-1)! %rここで、
rは、まだ関係のない要素の配列の次元です。
明確にするために、特定のケースを検討します。 たとえば、4つの位置にある4つの要素の24個の順列iЄ[0、23]のうち、17番目は次のシーケンスになります。
[17 //(4-1)!]%
R (0,1,2,3)= 2%4 = 2
(つまり、0から数えて、リストの3番目の要素は「2」です)。 この順列の次の要素は次のとおりです。
[17 //(3-1)!]%
R (0,1,3)= 8%3 = 2
(ここでも3番目の要素は「3」です)
同じ方法で続けると、結果として「2 3 1 0」の配列が得られます。 したがって、順列の数[
n!から
iのすべての値をループします
。 ]または配置[
n!/(nm)! 、ここで
mは配列内の位置の数]で、目的の組み合わせの完全なセットを取得します。
実際、コード自体は次のようになります。
import math elm=4
UPD:時間が経つにつれて、私はメソッドが十分にテストされていないことに気付きました-したがって、誰かがそれを使用し始めたら、警戒してください(誰もがっかりさせたくないでしょう)