単一ビットのカウントに関する詳細

8〜64ビットのサイズの変数の単一ビットをカウントするためのアルゴリズムへのアプローチのかなり完全な説明をしようとする記事をHabrコミュニティに提示したいと思います。 これらのアルゴリズムは、いわゆる「ビットマジック」または「ビットアルケミー」のセクションに属し、多くのプログラマーにその美しさと非自明性を魅了します。 この錬金術の基本に複雑なものは何もないことを示したいと思います。また、そのようなアルゴリズムを構成する基本的なテクニックに慣れることで、単一ビットをカウントする独自の方法を開発することさえできます。



始める前に、この記事はプログラミングの初心者向けではないことをすぐに警告したいと思います。 読者には、最も単純なビット操作（ビット単位の「and」、「or」、シフト）の概要を説明し、16進数システムの十分な知識があり、想像力を非常に自信を持って使用し、常に短いビットシーケンスではないことを示す必要があります。 可能であれば、すべてに写真が添付されますが、完全なプレゼンテーションを単純化するだけで、置き換えるものではありません。

説明されているすべての手法はC言語で実装され、32ビットと64ビットの2つのモードでテストされています。 したがって、この記事をよりよく理解するには、C言語を少なくともほぼ理解している方が良いでしょう。 テストは、64ビットWindows 7上のプロセッサCore 2 Duo E8400 @ 3GHzで行われました。プログラムのネットランタイムの測定は、 runexeユーティリティを使用して実行されました。 説明されたアルゴリズムのすべてのソースコードは、Yandexディスクのアーカイブで利用できます。そのコンパイルはVisual C ++、Intel C ++、GCC、およびCLangコンパイラでチェックされます。したがって、原則として、誰かが自宅で結果をダブルチェックしたい場合、問題はないはずです。 Linuxユーザーは、自分のシステムでプログラムのランタイムをテストする方法を私よりよく知っていると思うので、アドバイスはしません。

読者の中には、ビデオで同じものを見る方が簡単だと感じる人がいるかもしれません。 このようなビデオ（58分）を記録しましたが、プレゼンテーション形式では、テキストの下位にあるものとまったく同じものが設定されていますが、テキストを少し復活させようとしている間に、少しドライで厳格なスタイルである可能性があります。 したがって、誰にとってもより便利な方法で資料を研究してください。



錬金術の方法の1つまたは別のセットによって生成されたアルゴリズムを順番に説明します。各セクションには、異なるサイズの変数の動作時間を比較する表があり、最後にすべてのアルゴリズムの要約表があります。 すべてのアルゴリズムは、8〜64ビットの符号なし数値のエイリアスを使用します。

typedef unsigned char u8; typedef unsigned short int u16; typedef unsigned int u32; typedef unsigned long long u64; 

素朴なアプローチ

明らかに、ビット錬金術はインタビューで輝くために使用されるのではなく、プログラムを大幅に高速化するために使用されます。 何に関連する加速？ タスクをより詳細に掘り下げる時間がないときに思い浮かぶかもしれない些細なトリックに関連して。 このような手法は、ビットをカウントするための単純なアプローチです。数からビットを1つずつ「バイト」し、それらを要約して、数がゼロになるまで手順を繰り返します。

 u8 CountOnes0 (u8 n) { u8 res = 0; while (n) { res += n&1; n >>= 1; } return res; } 

私はこの些細なサイクルで何かにコメントする理由はないと思います。 nの最上位ビットが1の場合、サイクルは、最上位に達する前に数値のすべてのビットを通過する必要があることは肉眼で明らかです。

入力パラメーターu8のタイプをu16、u32、およびu64に変更すると、4つの異なる関数が得られます。 混oticとした方法で提示された2 ³²個の数字のストリームでそれらをそれぞれテストしましょう。 u8には256の異なる入力データがありますが、一貫性を保つために、これらすべての関数と後続のすべての関数に対して2 ^32個の乱数を実行し、常に同じ順序で実行します（詳細については、アーカイブのカリキュラムコードを参照してください） ）

次の表の時間は秒単位です。 テストでは、プログラムが3回実行され、平均時間が選択されました。 エラーはほとんど0.1秒を超えません。 最初の列はコンパイラモード（32ビットソースコードまたは64ビット）を反映し、4つの列が入力データの4つのバリアントを担当します。

モード	u8	u16	u32	u64
x86	38.18	72.00	130.49	384.76
x64	37.72	71.51	131.47	227.46

ご覧のとおり、操作の速度は入力パラメーターのサイズとともに非常に自然に増加します。 このオプションは、数値のサイズが64ビットで、計算がx86モードの場合、一般的な規則性から少し外れています。 入力パラメーターを2倍にすると、プロセッサーは4倍の作業を強いられることは明らかであり、3倍遅い速度でしか処理できないことも良いことです。

このアプローチの最初の利点は、実装時にミスを犯しにくいことです。そのため、この方法で作成されたプログラムは、より複雑なアルゴリズムをテストするためのリファレンスになります（これはまさに私の場合でした）。 2番目の利点は、汎用性と、あらゆるサイズの番号への比較的簡単な移植性です。

最下位ビットの「バイト」トリック

この錬金術の手法は、最下位ビットをリセットするという考えに基づいています。 数字nがあれば、数字nから最小の1つを取り、呪文n = n＆（n-1）を唱えることができます。 以下のn = 232の図は、このトリックについて最初に学んだ人々の状況を明確にします。


プログラムコードはあまり変更されていません。

 u8 CountOnes1 (u8 n) { u8 res = 0; while (n) { res ++; n &= n-1; //   . } return res; } 

これで、サイクルは数nの単位とまったく同じ回数実行されます。 これは、数値内のすべてのビットが単一である最悪の場合を排除しませんが、平均反復回数を大幅に削減します。 このアプローチは、プロセッサの苦痛を大幅に軽減しますか？ 実際にはそうではありませんが、8ビットではさらに悪化します。 結果の概要テーブルは最後になりますが、ここでは各セクションに独自のテーブルがあることに注意してください。

モード	u8	u16	u32	u64
x86	44.73	55.88	72.02	300.78
x64	40.96	69.16	79.13	126.72

事前計算

急いで「ハード」スペルに切り替えるのではなく、最も経験の浅い魔術師でさえも救うことができる最後の簡単なトリックを考えてみましょう。 この問題の解決策はビット錬金術に直接適用されませんが、完全を期すために、画像は必ず考慮する必要があります。 256と65536の値を持つ2つのテーブルを開始します。このテーブルでは、考えられるすべての1バイトと2バイトの値に対する回答がそれぞれ事前に計算されます。

  u8 BitsSetTableFF[256]; //       u8 BitsSetTableFFFF[65536]; //       

これで、1バイトのプログラムは次のようになります。

  u8 CountOnes2_FF (u8 n) { return BitsSetTableFF[n]; } 

より大きな数のビット数を計算するには、バイトに分割する必要があります。 たとえば、u32の場合、次のようなコードがあります。

  u8 CountOnes2_FF (u32 n) { u8 *p = (u8*)&n; n = BitsSetTableFF[p[0]] + BitsSetTableFF[p[1]] + BitsSetTableFF[p[2]] + BitsSetTableFF[p[3]]; return n; } 

または、2バイトの事前計算テーブルを使用する場合：

  u8 CountOnes2_FFFF (u32 n) { u16 *p = (u16*)&n; n = BitsSetTableFFFF[p[0]] + BitsSetTableFFFF[p[1]]; return n; } 

さて、あなたはそれを推測しました、各オプションの入力パラメーターnのサイズ（8ビットを除く）には、使用する2つのテーブルのどちらかに応じて、事前計算のための2つのオプションがあります。 読者はBitsSetTableFFFFFFFFテーブルを取得および取得できない理由を理解していると思いますが、これが正当化される問題がある可能性があります。

事前計算は高速に機能しますか？ すべてサイズに依存します。以下の表を参照してください。 最初はシングルバイトの事前計算用で、2番目はダブルバイト用です。

モード	u8	u16	u32	u64
x86	0.01	1.83	21.07	36.25
x64	0.01	1.44	24.79	26.84

興味深い点：x64モードの場合、u64の事前計算ははるかに高速です。おそらくこれらは最適化機能ですが、これは2番目の場合には現れません。

モード	u8	u16	u32	u64
x86	---	0.05	7.95	13.01
x64	---	0,07	8.49	13.01

重要な注意：事前計算を使用するこのアルゴリズムは、次の2つの条件が満たされている場合にのみ有益です： （1）追加のメモリがある場合、 （2）単一ビットの数をテーブル自体のサイズよりもはるかに多く計算する必要がある場合、つまりいくつかの単純なアルゴリズムをテーブルに事前入力するのに費やした時間を「取り戻す」。 おそらく、実際には常に満たされているエキゾチックな条件を念頭に置くこともできます。 メモリ自体へのアクセスが迅速であり、他のシステム機能の動作が遅くならないようにする必要があります。 実際には、テーブルにアクセスすると、元々そこにあったものがキャッシュからスローされ、他のコードの一部が遅くなる可能性があります。 横棒をすぐに見つけることはまずありませんが、通常のプログラムを実装する場合、実際にこのような巨大な最適化を必要とする人はほとんどいません。

乗算と除算の剰余

最後に、錬金術連隊からより強力なポーションを取りましょう。 乗算と、ユニットなしの2の累乗による除算の残りの助けを借りて、非常に興味深いことができます。 1バイトの呪文のキャストを始めましょう。 便宜上、「a」から「h」までのラテン文字で1バイトのすべてのビットを示します。 番号nは次の形式になります。


乗算n '=n⋅0x010101（たとえば、接頭辞「0x」を使用して、16進数を表します）は、3バイトで1バイトを「複製」するだけです。

ここで、24ビットを精神的に各3ビットの8ブロックに分割します（次の図、プレートの最初の行を参照）。 次に、マスク0x249249（プレートの2行目）でビット単位の「and」を使用して、各ブロックの2つの上位ビットをゼロにします。


表の3行目は、マスクの16進表記法を説明しています。 最後の行は、達成した結果を示しています。元のバイトのすべてのビットは、それぞれ独自の3ビットブロックに含まれていますが、順序は異なります（順序は重要ではありません）。

ここで注意：これら8つのブロックを追加する必要があります-そして、ビットの合計を取得します！

ある数Aを2 ^k -1で除算した余りが、同じく数2の-1を法とする数Aのkビットブロックの合計を与えることがわかります。

つまり、受け取った数から、2 ³ -1（7）で割った余りを取得する必要があります。8ブロックの合計は7を法としています。この場合、ビットの合計は7または8になる可能性があります。アルゴリズムはそれぞれ0と1を返します。 しかし、見てみましょう：どのような場合に答え8を得ることができますか？ n = 255の場合のみ。 そして、どの場合に0を取得できますか？ n = 0の場合のみ。 したがって、7の剰余を取った後のアルゴリズムが0を与える場合、入力でn = 0を受け取ったか、または数に正確に7単位ビットがあります。 この推論を要約すると、次のコードが得られます。

 u8 CountOnes3 (u8 n) { if (n == 0) return 0; //  ,   0. if (n == 0xFF) return 8; //  ,   8. n = (0x010101*n & 0x249249) % 7; //      7. if (n == 0) return 7; //   7  . return n; // ,     1  6  . } 

nのサイズが16ビットの場合、8ビットの2つの部分に分割できます。 たとえば、次のように：

 u8 CountOnes3 (u16 n) { return CountOnes3 (u8(n&0xFF)) + CountOnes3 (u8(n>>8)); 

32ビットと64ビットの場合、そのようなパーティションは理論的にも意味がありません。3回の分岐での乗算と除算の残りは、4回または8回連続で実行されると非常に高価になります。 しかし、私はあなたのために空の場所を下の表に残したので、もしあなたが私を信じないなら、自分でそれらを記入してください。 同様のプロセッサを使用している場合、CountBits1プロシージャに匹敵する結果が得られる可能性が最も高くなります（ここでSSEを使用した最適化の可能性については話していないが、これは別の問題です）。

モード	u8	u16	u32	u64
x86	12,42	30.57	---	---
x64	13.88	33.88	---	---

もちろん、このトリックは分岐せずに実行できますが、ブロックに数値を分割するとき、0から8までのすべての数値がブロックに含まれている必要があり、これは4ビットブロック（およびそれ以上）の場合にのみ達成できます。 4ビットブロックの合計を実行するには、数値を正しく「複製」する係数を選択し、2 ⁴ -1 = 15による除算の残りを取得して、結果のブロックを追加する必要があります。 経験豊富な錬金術師（数学を知っている）は、0x08040201のような要素を簡単に見つけることができます。 なぜ彼はこのように選ばれたのですか？


実際には、元の数のすべてのビットが4ビットブロックの正しい位置を占める必要があり（上の図）、8と4は比較的素数ではないため、通常の8ビットの4回のコピーでは正しい場所が得られませんビット。 9は相互に単純な4であるため、バイトにゼロを1つ追加する必要があります。つまり、9ビットを複製するために、サイズは36ビットですが、元のバイトのすべてのビットが4ビットブロックの下位にある数値を取得します。 各ブロックの3つの最上位ビットをリセットするために、0x111111111（上の図の2行目）のビット単位の「and」を取るだけです。 次に、ブロックを折り畳む必要があります。

このアプローチを使用すると、バイト内の単一ビットを計算するプログラムは非常に簡単になります。

 u8 CountOnes3_x64 (u8 n) { return ((u64)0x08040201*n & 0x111111111) % 15; } 

プログラムの欠点は明らかです。64ビットの算術演算を行って、その後の結果をすべて行う必要があります。 実際には、このプログラムは64のうち33ビットのみを使用することに気付きます（最上位3ビットはリセットされます）。原則として、これらの計算を32ビット算術に転送する方法を理解できますが、そのような最適化に関する話はこのトピックには含まれていませんガイド。 とりあえず、テクニックを勉強してみましょう。特定のタスクのために既に自分でそれらを最適化する必要があります。

このトリックが正しく機能するように、変数nのサイズの問題に答えます。 15で除算した残りの部分を使用するため、このような変数は14ビットを超えるサイズを持つことはできません。そうしないと、以前と同様に分岐を適用する必要があります。 ただし、14ビットの場合、すべてのビットが所定の位置に収まるように14ビットに1つのゼロを追加すると、受信が機能します。 ここで、全体として、受信の本質を学び、複製の乗数と不要なビットを自分でリセットするためのマスクを簡単に選択できると仮定します。 完成した結果をすぐに表示します。

 u8 CountOnes3_x64 (u14 n) { //    (   )! return (n*0x200040008001llu & 0x111111111111111llu) % 15; } 

上記のプログラムは、14ビットの変数が符号なしの場合、コードがどのように見えるかを示しています。 同じコードが15ビットの変数で機能しますが、そのうちの14のみが1に等しいという条件の下で、またはn = 0x7FFFの場合を個別に調べます。 タイプu16の変数に正しいコードを書き込むには、これらすべてを理解する必要があります。 アイデアは、最初に最下位ビットを「噛んで」、残りの15ビット数のビットをカウントしてから、「ビットオフ」ビットを追加し直すことです。

 u8 CountOnes3_x64 (u16 n) { u8 leastBit = n&1; //   . n >>= 1; //   15   . if (n == 0) return leastBit; //   0,     . if (n == 0x7FFF) return leastBit + 15; //  ,   15+ . return leastBit + (n*0x200040008001llu & 0x111111111111111llu) % 15; //  ( 14+ ). } 

n 32ビットの場合、より深刻な顔を既に思い浮かべる必要があります...最初に、答えは6ビットのみに収まりますが、n = 2 ³² -1の別のケースを考慮し、5ビットのフィールドで冷静に計算を行うことができます。 これによりスペースが節約され、nの32ビットフィールドをそれぞれ12ビットの3つの部分に分割できます（はい、最後のフィールドは完全ではありません）。 12⋅5= 60なので、1つの12ビットフィールドを5回複製して係数を選択し、5ビットブロックを追加して、残りの31で除算します。これを各フィールドで3回行う必要があります。 結果を要約すると、次のコードが得られます。

 u8 CountOnes3_x64 ( u32 n ) { if (n == 0) return 0; if (n + 1 == 0) return 32; u64 res = (n&0xFFF)*0x1001001001001llu & 0x84210842108421llu; res += ((n&0xFFF000)>>12)*0x1001001001001llu & 0x84210842108421llu; res += (n>>24)*0x1001001001001llu & 0x84210842108421llu; res %= 0x1F; if (res == 0) return 31; return res; } 

ここでも同様に、3つのブランチの代わりに、除算から3つの残基を取ることができましたが、ブランチオプションを選択しました。これは、私のプロセッサでより良く機能します。

64ビットのサイズであるnについては、乗算や加算がそれほど多くない適切な呪文を思い付くことができませんでした。 6または7のいずれかが判明し、これはこのようなタスクには多すぎます。 もう1つのオプションは、128ビット演算を使用することですが、それがどのような「ロールバック」を行うのかわからないため、準備のできていないメイジを壁に投げることができます:)

仕事の時間をよく見てみましょう。

モード	u8	u16	u32	u64
x86	39.78	60.48	146.78	---
x64	6.78	12.28	31.12	---

この表から明らかな結論は、一般的にアルゴリズムは悪くないものの、32ビット実行モードでは64ビット演算はあまり認識されないということです。 ケースu32（24.79 s）のシングルバイトテーブルのx64モードでの事前計算アルゴリズムの速度を思い出せば、このアルゴリズムはわずか25％遅れていることがわかり、これが次のセクションで具体化された競争の理由です。

剰余を乗算とシフトに置き換える

残りを取得する操作の欠点は誰にとっても明らかです。 これは部門であり、部門は長いです。 もちろん、現代のコンパイラーは錬金術を知っており、除算を乗算とシフトで置き換える方法を知っており、剰余を得るには、除数から除数を掛けた商を引く必要があります。 しかし、それはまだ長い時間です！ コードスペルキャスターの古代の巻物には、以前のアルゴリズムを最適化する興味深い方法が保存されていました。 kビットブロックを要約するには、除算の残りの部分を使用するのではなく、ブロックを追加してビットをリセットするマスクによる別の乗算を使用します。 サイズがn 1バイトの場合、次のようになります。

まず、バイトを再度3回複製し、上記で既に渡された式0x010101⋅n＆0x249249を使用して、各3ビットブロックの最上位2ビットを削除します。


便宜上、各3ビットブロックに大文字のラテン文字を付けました。 次に、結果に同じマスク0x249249を掛けます。 マスクは各3番目の位置に1つのビットを含むため、この乗算はそれ自体の数を8回加算するのと同じで、毎回3ビットのシフトがあります。


何が見えますか？ ビット21から23は適切な量を提供します！ さらに、右側のブロックのオーバーフローは、どのブロックにも7を超える数がないため、不可能です。唯一の問題は、合計が8の場合、0が得られることですが、ケースは個別に検討できます。

 u8 CountOnes3_x64_m (u8 n) { if (n == 0xFF) return 8; return ((u64(0x010101*n & 0x249249) * 0x249249) >> 21) & 0x7; } 

実際、前のセクションのコードを使用し、乗算、シフト、およびビット単位の「And」による7での除算の残りを最後に使用することで置き換えました。 ただし、3つのブランチの代わりに、1つだけが残ります。

同様のプログラムを16ビットでコンパイルするには、前のセクションのコードを使用する必要があります。このセクションでは、15による除算の残りを取得してこの手順を乗算に置き換える方法を示します。 同時に、どの条件をコードから削除できるかを簡単に確認できます。

 u8 CountOnes3_x64_m (u16 n) { u8 leastBit = n&1; //    n >>= 1; //   15 . return leastBit + (( (n*0x200040008001llu & 0x111111111111111llu)*0x111111111111111llu >> 56) & 0xF); //  ( 15 +  ). } 

32ビットについても同じことを行います。前のセクションのコードを使用し、紙に少し書いて、剰余を乗算に置き換えた場合のシフトがどうなるかを理解します。

 u8 CountOnes3_x64_m ( u32 n ) { if (n+1 == 0) return 32; u64 res = (n&0xFFF)*0x1001001001001llu & 0x84210842108421llu; res += ((n&0xFFF000)>>12)*0x1001001001001llu & 0x84210842108421llu; res += (n>>24)*0x1001001001001llu & 0x84210842108421llu; return (res*0x84210842108421llu >> 55) & 0x1F; } 

64ビットの場合、プロセッサをストーブとして機能させないようなものも思いつきませんでした。

モード	u8	u16	u32	u64
x86	12.66	42.37	99.90	---
x64	3,54	4,51	18.35	---

x64モードの結果に喜んで驚いた。 予想どおり、u32の場合、1バイトのテーブルを使用して事前計算をやり直しました。 事前計算を追い越すことさえ可能ですか？ 良い質問:)

並列加算

おそらくこれが最も一般的なトリックであり、非常に多くの場合、経験の少ないスペルキャスターが次々に繰り返し、正確に機能する方法を理解していません。

1バイトから始めましょう。 バイトは2ビットの4つのフィールドで構成され、最初にこれらのフィールドのビットを加算して、次のように言います。

 n = (n>>1)&0x55 + (n&0x55); 

以下に、この操作の説明図を示します（前と同様に、1バイトのビットを最初のラテン文字で示します）。

1つのビット単位のANDは各2ビットブロックの下位ビットのみを残し、2番目は上位ビットを残しますが、それらを下位ビットに対応する位置にシフトします。合計の結果として、各2ビットブロック（上の図の最後の行）の隣接ビットの合計を取得します。

次に、2ビットフィールドの数値をペアにして、結果を2つの4ビットフィールドに入れます。

 n = (n>>2)&0x33 + (n&0x33); 

次の図は結果を説明しています。私はこれ以上苦労せずに今持ってきます：

最後に、4ビットフィールドに2つの数値を追加します。

 n = (n>>4)&0x0F + (n&0x0F); 

同様に、2の累乗に等しい任意のビット数に受信を拡張できます。スペル行の数は、ビット数の2進対数です。アイデアを理解したら、以下に記述されている4つの関数を簡単に見て、理解が正しいことを確認してください。

 u8 CountOnes4 (u8 n) { n = ((n>>1) & 0x55) + (n & 0x55); n = ((n>>2) & 0x33) + (n & 0x33); n = ((n>>4) & 0x0F) + (n & 0x0F); return n; } 

 u8 CountOnes4 (u16 n) { n = ((n>>1) & 0x5555) + (n & 0x5555); n = ((n>>2) & 0x3333) + (n & 0x3333); n = ((n>>4) & 0x0F0F) + (n & 0x0F0F); n = ((n>>8) & 0x00FF) + (n & 0x00FF); return n; } 

 u8 CountOnes4 (u32 n) { n = ((n>>1) & 0x55555555) + (n & 0x55555555); n = ((n>>2) & 0x33333333) + (n & 0x33333333); n = ((n>>4) & 0x0F0F0F0F) + (n & 0x0F0F0F0F); n = ((n>>8) & 0x00FF00FF) + (n & 0x00FF00FF); n = ((n>>16) & 0x0000FFFF) + (n & 0x0000FFFF); return n; } 

 u8 CountOnes4 (u64 n) { n = ((n>>1) & 0x5555555555555555llu) + (n & 0x5555555555555555llu); n = ((n>>2) & 0x3333333333333333llu) + (n & 0x3333333333333333llu); n = ((n>>4) & 0x0F0F0F0F0F0F0F0Fllu) + (n & 0x0F0F0F0F0F0F0F0Fllu); n = ((n>>8) & 0x00FF00FF00FF00FFllu) + (n & 0x00FF00FF00FF00FFllu); n = ((n>>16) & 0x0000FFFF0000FFFFllu) + (n & 0x0000FFFF0000FFFFllu); n = ((n>>32) & 0x00000000FFFFFFFFllu) + (n & 0x00000000FFFFFFFFllu); return n; } 

並列加算はそこで終わりません。このアイデアは、各ビットで同じビットマスクが2回使用されることを観察することで開発できます。可能ですが、すぐにはできません。u32のコードを例にとると、次のことができます（コメントを参照）。

 u8 CountOnes4 (u32 n) { n = ((n>>1) & 0x55555555) + (n & 0x55555555); //     n = ((n>>2) & 0x33333333) + (n & 0x33333333); //   n = ((n>>4) & 0x0F0F0F0F) + (n & 0x0F0F0F0F); //   &   n = ((n>>8) & 0x00FF00FF) + (n & 0x00FF00FF); //   &   n = ((n>>16) & 0x0000FFFF) + (n & 0x0000FFFF); //    & return n; //    8-  . } 

演習として、次のコードが前のコードを正確に反映する理由を自分で証明したいと思います。最初の行では、ヒントを示しますが、すぐには調べません。

 u8 CountOnes4_opt (u32 n) { n -= (n>>1) & 0x55555555; n = ((n>>2) & 0x33333333 ) + (n & 0x33333333); n = ((n>>4) + n) & 0x0F0F0F0F; n = ((n>>8) + n) & 0x00FF00FF; n = ((n>>16) + n); return n; } 

他のデータ型でも同様の最適化オプションが可能です。

2つのテーブルを以下にリストします。1つは通常の並列合計用、もう1つは最適化用です。

モード	u8	u16	u32	u64
x86	7.52	14.10	21.12	62.70
x64	8.06	11.89	21.30	22.59

モード	u8	u16	u32	u64
x86	7.18	11.89	18.86	65.00
x64	8.09	10.27	19,20	19,20

一般に、最適化されたアルゴリズムはうまく機能しますが、u64のx86モードでは通常のアルゴリズムに負けています。

組み合わせた方法

単一ビットをカウントするための最適なオプションは、並列法（最適化あり）と、ブロックの合計を計算する乗算を伴う複製法であることがわかります。両方の方法を組み合わせて、組み合わせたアルゴリズムを取得できます。

最初に行うことは、並列アルゴリズムの最初の3行を完了することです。これにより、数値の各バイトの正確なビット数がわかります。たとえば、u32の場合、次の手順を実行します。

  n -= (n>>1) & 0x55555555; n = ((n>>2) & 0x33333333) + (n & 0x33333333); n = (((n>>4) + n) & 0x0F0F0F0F ); 

これで、数値nは4バイトで構成されます。これは、4つの数値と見なされる必要があり、その合計が探しています。


数値nに0x01010101を掛けると、これらの4バイトの合計を見つけることができます。あなたは今、そのような乗算が何を意味するのかをよく理解しています、答えがどこにあるかを決定する便宜のために、私は絵を引用します：


答えは3バイトです（0から数える場合）。したがって、u32の組み合わせたトリックは次のようになります。

 u8 CountOnes5 ( u32 n ) { n -= (n>>1) & 0x55555555; n = ((n>>2) & 0x33333333 ) + (n & 0x33333333); n = ((((n>>4) + n) & 0x0F0F0F0F) * 0x01010101) >> 24; return n; //      8  . } 

彼はu16です。

 u8 CountOnes5 (u16 n) { n -= (n>>1) & 0x5555; n = ((n>>2) & 0x3333) + (n & 0x3333); n = ((((n>>4) + n) & 0x0F0F) * 0x0101) >> 8; return n; //      8  . } 

彼はu64です。

 u8 CountOnes5 ( u64 n ) { n -= (n>>1) & 0x5555555555555555llu; n = ((n>>2) & 0x3333333333333333llu ) + (n & 0x3333333333333333llu); n = ((((n>>4) + n) & 0x0F0F0F0F0F0F0F0Fllu) * 0x0101010101010101) >> 56; return n; //      8  . } 

このメソッドの速度は、ファイナルテーブルですぐに確認できます。

最終比較

以下の2つの表を調べて、興味のある独自の結論を出すことを読者に提案します。それらの中で、プログラムを実装するメソッドの名前を指定し、それぞれの特定のケースで最良と思われるアプローチを長方形の枠でマークしました。事前計算が常に勝ちだと思っていた人は、x64モードでは少し驚きます。

x86コンパイルモードの最終比較。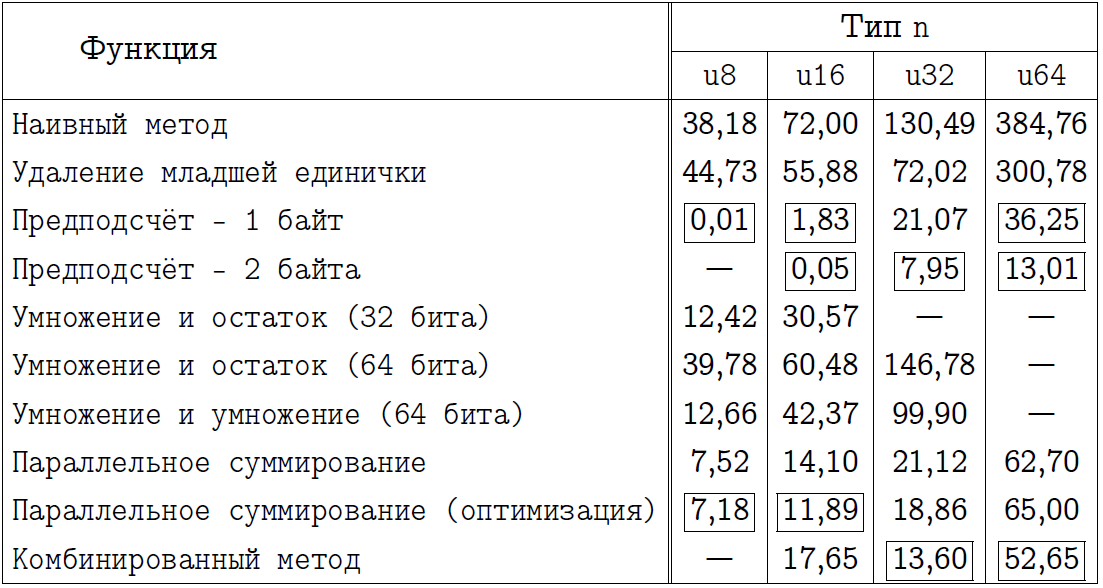


x64コンパイルモードの最終比較。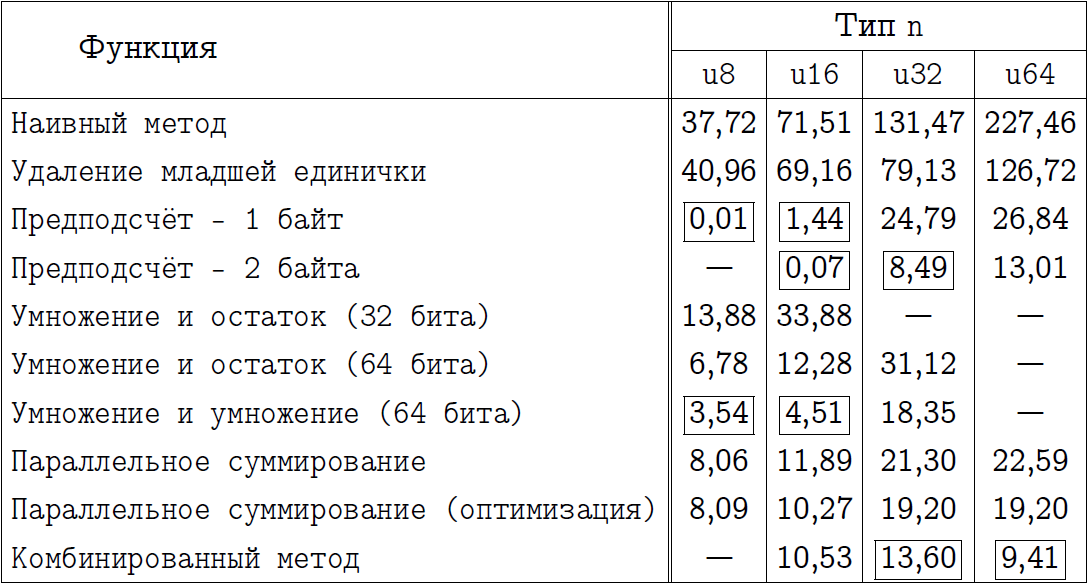

発言

いずれにしても、ファイナルテーブルを何らかのアプローチを支持する証拠と見なさないでください。プロセッサとコンパイラでは、このようなテーブルのいくつかの数値は完全に異なると信じてください。残念ながら、どのアルゴリズムがいずれの場合でもより良くなると確信することはできません。タスクごとに特定の方法を強化する必要があり、残念ながら、普遍的な高速アルゴリズムは存在しません。

私は自分自身について知っているアイデアの概要を説明しましたが、これらは異なる組み合わせでの特定の実装が非常に異なる可能性があるアイデアです。これらのアイデアをさまざまな方法で組み合わせると、単一のビットをカウントするための膨大な数のさまざまなアルゴリズムを取得できます。それぞれのアルゴリズムは、場合によっては適切であることがわかります。

ご清聴ありがとうございました。 じゃあね！

UPD：SSE4.2をサポートするプロセッサがないため、SSE4.2からのPOPCNT命令はテストリストに含まれていません。