いくつかの変数の関数の別の多項式近似

引数の特定のセットの関数の特定の値によって関数を補間する問題では、特定の点で検討中の関数の値と一致する多項式で関数を近似する式が広く使用されています。

このタイプの近似は、科学計算で広く使用されています。

例：各引数値に対して関数を計算するのは非常にコストがかかります（そして、たとえばNが多くあります）。したがって、値のテーブルが作成され、必要に応じて、関数の値が特定のポイントで取得され、プレートから補間されます。 もちろん、テーブルの初期構築と補間手順（N回）は、関数自体の正確な計算をN回行うよりも「安く」する必要があります。

この式をいくつかの変数の関数の場合に一般化します

ベクトルのスカラー積は、引数Dxの値の分散の平方を考慮して計算されます

• 引数の各座標の等価性を考慮するために、Dx [k] = M2 [k]-M1 [k] ∗ M1 [k]を計算します
• <A; B> = SUM A [k] * B [k] / Dx [k]

アルゴリズム

1.与えられたベクトルXiについて、引数値の分散の二乗のベクトルDxを計算します
2.ベクトルXの場合、最も近いポイントX1、...、Xpのpを見つけます。ここで、ポイント間の距離は、引数値の分散の2乗を考慮して計算されます
3.多項式P（X）= SUM Yi *<X-Xj、Xi-Xj> / <Xi-Xj、Xi-Xj>の値を計算します。ここで、スカラー積は、引数の値の分散の2乗を考慮して計算されます

2つの変数の関数の近似デモンストレーション

history.txt

• -1 -1 -10
• 1 1 10
• 0 0 0
• -1 1 -8
• 1 -1 -20

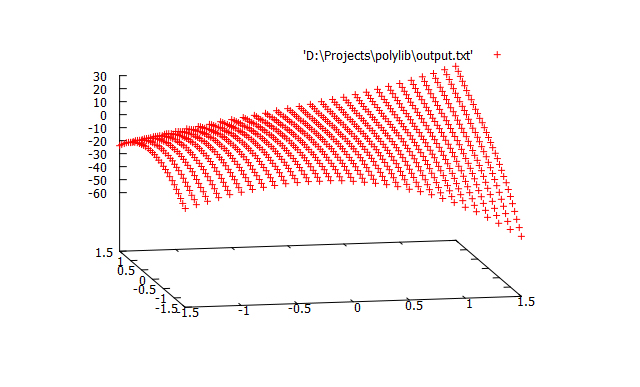
gnuplotプログラムでステップ0.1でラティスに多項式値をプロットします

• predict.exe -history history.txt -input input.txt -output output.txt -p 5
• splot "output.txt"

// predict.cpp:      . // #include "stdafx.h" struct t_previous_result { std::vector<double> x; double y; }; ///////////////////////////////////////////////////////// //        double delta(std::vector<double>& a, std::vector<double>& b, std::vector<double>& dx) { auto s = 0.0; auto i = 0; for (; i < a.size() && i < b.size() && i < dx.size(); i++) if (dx[i] > 0.0) s += (a[i] - b[i]) * (a[i] - b[i]) / dx[i]; for (; i < a.size() && i < dx.size(); i++) if (dx[i] > 0.0) s += a[i] * a[i] / dx[i]; for (; i < b.size() && i < dx.size(); i++) if (dx[i] > 0.0) s += b[i] * b[i] / dx[i]; return s; } ///////////////////////////////////////////////////////// //      double scalar(std::vector<double>& a, std::vector<double>& b, std::vector<double>& dx) { auto s = 0.0; auto i = 0; for (; i < a.size() && i < b.size() && i < dx.size(); i++) if (dx[i] > 0.0) s += (a[i] * b[i]) / dx[i]; return s; } ///////////////////////////////////////////////////////// //          double predict(std::vector<double>& x, std::vector<t_previous_result>& previous_results, std::vector<double>& dx, int p) { std::vector<std::pair<t_previous_result, double>> neighbors; for (auto it = previous_results.begin(); it != previous_results.end(); ++it) { std::vector<double>& x2 = it->x; auto d = delta(x, x2, dx); std::pair<t_previous_result, double> pair(*it, d); neighbors.push_back(pair); } std::sort(neighbors.begin(), neighbors.end(), [](std::pair<t_previous_result, double> const& a, std::pair<t_previous_result, double> const& b) { return (a.second < b.second); }); neighbors.resize(std::min(p, static_cast<int>(neighbors.size()))); auto y = 0.0; for (auto iti = neighbors.begin(); iti != neighbors.end(); ++iti) { auto s = iti->first.y; std::vector<double>& xi = iti->first.x; for (auto itj = neighbors.begin(); itj != neighbors.end(); ++itj) { if (iti == itj) continue; std::vector<double>& xj = itj->first.x; std::vector<double> xxj; std::vector<double> xixj; for (auto i = 0; i < x.size() && i < xj.size(); i++) xxj.push_back(x[i] - xj[i]); for (auto i = 0; i < xi.size() && i < xj.size(); i++) xixj.push_back(xi[i] - xj[i]); s *= scalar(xxj, xixj, dx) / scalar(xixj, xixj, dx); } y += s; } return y; } ///////////////////////////////////////////////////////// //   static const int _p = 3; int main(int argc, char* argv[]) { std::vector<t_previous_result> previous_results; std::vector<double> dx; char* input_file_name = nullptr; char* output_file_name = nullptr; char* previous_results_file_name = nullptr; auto p = _p; std::string line; //     Windows //  setlocale()   ,   -   ,    LC_TYPE -  ,   —  . //      "Russian",     ,          . setlocale(LC_ALL, ""); for (auto i = 1; i < argc; i++) { if (strcmp(argv[i], "-help") == 0) { std::cout << "Usage :\t" << argv[0] << " [-input <inputfile>] [-output <outputfile>] [...]" << std::endl; } else if (strcmp(argv[i], "-input") == 0) input_file_name = argv[++i]; else if (strcmp(argv[i], "-output") == 0) output_file_name = argv[++i]; else if (strcmp(argv[i], "-history") == 0) previous_results_file_name = argv[++i]; else if (strcmp(argv[i], "-p") == 0) p = atoi(argv[++i]); } if (input_file_name != nullptr) freopen(input_file_name, "r", stdin); if (output_file_name != nullptr) freopen(output_file_name, "w", stdout); if (previous_results_file_name != nullptr) { std::vector<double> m1; std::vector<double> m2; std::ifstream history(previous_results_file_name); if (!history.is_open()) throw "Error opening file"; while (std::getline(history, line)) { std::stringstream ss(line); std::vector<double> x; std::copy(std::istream_iterator<double>(ss), std::istream_iterator<double>(), std::back_inserter(x)); auto y = x.back(); x.pop_back(); t_previous_result previous_result; previous_result.x = x; previous_result.y = y; previous_results.push_back(previous_result); for (auto i = 0; i < x.size(); i++) { if (i >= m1.size()) m1.push_back(0.0); if (i >= m2.size()) m2.push_back(0.0); m1[i] += x[i]; m2[i] += x[i] * x[i]; } } for (auto it = m1.begin(); it != m1.end(); ++it) *it /= previous_results.size(); for (auto it = m2.begin(); it != m2.end(); ++it) *it /= previous_results.size(); for (auto i = 0; i < m1.size() && i < m2.size(); i++) dx.push_back(m2[i] - m1[i] * m1[i]); } while (std::getline(std::cin, line)) { double y; std::vector<double> x; std::stringstream ss(line); std::copy(std::istream_iterator<double>(ss), std::istream_iterator<double>(), std::back_inserter(x)); y = predict(x, previous_results, dx, p); for (auto it = x.begin(); it != x.end(); ++it) std::cout << *it << ' '; std::cout << y << std::endl; } return 0; } 

プロジェクトのインターネットアドレス： https : //github.com/dprotopopov/polylib

使用したソフトウェア

• Microsoft Visual Studio 2013-プログラミング環境
• gnuplot-クロスプラットフォームのチャート作成ツールwww.gnuplot.info