数学者プログラマーの生活の中で数時間、またはウィキペディアを読む

まず、 ロックンロールナードをエピグラフとして引用します 。

-こんにちは、私の名前は％username％であり、そこで何が起こっているのかを理解するために、シグマ表記の金額を紙に密かに公開します。
-こんにちは、％username％！

ですから、前回の記事で述べたように、数学を恐れるパニックな生徒がいますが、趣味としてはんだごてを選び、今ではセグウェイカートを組み立てたいと思っています。 彼らはそれを集めましたが、彼女はバランスを保ちたくありません。 彼らはPIDコントローラーを使用することを考えましたが、うまく機能するように係数を選択できませんでした。 アドバイスを求めに来てください。 しかし、制御理論では一般的にブームブームに近づきませんでした。 しかし、ハブで一度、線形二次レギュレータが著者を助けたが、pidは役に立たなかったという記事を見ました 。

それでも指にPIDがあると想像すると（ ここに私の記事がありますが、これはある種の時計への恐怖に転じたものです）、他の制御方法についても聞いていませんでした。 したがって、私のタスクは、線形2次レギュレータが何であるかを想像することです（そして、同時に学生に説明します）。 これまでのところ、鉄を使った仕事はありません。文学を使って仕事をする方法を示します。これが私の仕事の大部分を占めるからです。

私の作品についての露出主義がなくなったので、ここに私の職場があります（クリック可能）：

使用したソース

それで、私が最初にすることは、 ウィキペディアに行くことです。 ロシアのウィキペディアは残酷で容赦ないので、私たちは英語のテキストのみを読みます。 彼も嫌なのですが、まだそうではありません。 だから、読んだ。 すべての入門テキストブリックのうち、私に興味を持っているフレーズは1つだけです。

最適制御の理論は、動的システムを最小コストで運用することに関するものです。 システムダイナミクスが一連の線形微分方程式で記述され、コストが2次関数で記述される場合は、LQ問題と呼ばれます。

ロシア語に翻訳すると、彼らは微分方程式（ある恐怖）によって特定の動的システムをモデル化し、制御を直接選択して、ある種の2次関数を最小化すると言います（ああ！最小二乗近似を感じます）。 いいね さらに読み込もう：

有限地平線、連続時間LQR、
[一連のひどい数式]

私たちはそれをスキップします、それは沼でのそのような読み取りです、さらに、あなたの手で連続的な機能を考慮することは明らかにうんざりするでしょう。

無限の地平線、連続時間LQR、
[さらに恐ろしい式のシリーズ]

1時間ごとは簡単ではなく、不適切な積分がなくなったため、スキップすると、突然さらに興味深いものが見つかります。

有限時間、離散時間LQR

ああ、それが大好きです。 離散システムがあり、一定の間隔（最初の読み取りの一部の間隔は常に1秒に等しい）で状態を調べます。 方程式の導関数はなくなりました。なぜなら、 現在、（x_ {k + 1} -x_ {l}）/ 1秒として近似できます。 ここで、x_kが何であるかを理解しておくといいでしょう。

一次元の例

ファインマンは、すべての方程式をどのように読むか、彼がしなければならないことを正確に書いた。

実際、私の推測には一定量の本物の品質がありました。 誰かが説明しているときに今日も使っているスキームがありました
私が理解しようとしていること：私は例を作り続けています。 例えば、数学者は素晴らしい定理を持ち込み、彼らは皆興奮しています。 定理の条件を教えてくれるので、すべての条件に合うものを構築します。 セット（1つのボール）-バラバラ（2つのボール）があります。 それから、ボールは私の頭の中で色を変えたり、髪の毛などを成長させたりします。 最後に彼らは定理を述べています。これは私の毛むくじゃらの緑色のボールの事には当てはまらないボールについての馬鹿げたことです。

まあ、私たちはファインマンよりもクールですか？ 個人的にはそうではありません。 それではこれをやろう。 ある初速度で走行している車があります。 タスクは、特定の最終速度まで加速することですが、影響を与えることができるのは、アクセルペダルまたは車の加速だけです。

車が完璧で、この法則に従って動くと想像してみましょう。


x_kは1秒あたりの車の速度k、u_kは必要なアクセルペダルの位置です。1秒あたりの加速度kとして解釈できます。 合計で、特定の速度x_0で開始し、次にそのような数値積分を実行します（どの単語に入ったのか）。 m / sおよびm / s ^ 2を追加しないことに注意してください。u_kには、測定間隔の1秒が乗算されます。 デフォルトでは、すべての係数が0または1のいずれかです。

それで、何が起こっているのかを理解するために、私はこの種のコードを書いてい ます （私は書いた直後に捨てる1回限りのコードをたくさん書いています）。 念のためここにリストしますが、いつものように、 OpenNLを使用して大規模なスパース線形方程式を解きます。



だから、私がやっていることを理解しましょう。 はじめに、N = 60と言います。すべてに60秒かかります。 それから私は、最終速度は毎秒2.3メートル、最初の毎秒0.5メートルであるべきだと言います。これはブルドーザーから設定されます。 60 * 2の変数-60の速度値と60の加速度値（厳密に言えば、59の加速度があるはずですが、60があり、最後は厳密に0であると言う方が簡単です）。

合計、2 * N個の変数（N = 60）があり、偶数の変数（通常のプログラマーのようにゼロからカウントを開始）は速度であり、奇数の変数は加速です。 これらの行で初期速度と最終速度を設定します。
実際、私は初期速度をx0（.5m / s）に、そして最終的な-xN（2.3m / s）にしたいと言った。

  nlBegin(NL_ROW); // x0 = x0 nlCoefficient(0, 1); nlRightHandSide(x0); nlScaleRow(hard_penalty); nlEnd(NL_ROW); nlBegin(NL_ROW); // xN = xN nlCoefficient((N-1)*2, 1); nlRightHandSide(xN); nlScaleRow(hard_penalty); nlEnd(NL_ROW); 

x {i + 1} = xi + uiであることがわかっているので、システムにN-1個のそのような方程式を追加しましょう。

  for (int i=0; i<N-1; i++) { nlBegin(NL_ROW); // x{i+1} = xi + ui nlCoefficient((i+1)*2 , -1); nlCoefficient((i )*2 , 1); nlCoefficient((i )*2+1, 1); nlScaleRow(hard_penalty); nlEnd(NL_ROW); } 

それで、私たちはすべての厳しい制限をシステムに追加しました、そして実際、正確に最適化したいものは何ですか？ x_iをできるだけ早く最終速度xNに到達させたいと言って始めましょう。

  for (int i=0; i<N; i++) { nlBegin(NL_ROW); // xi = xN, soft nlCoefficient(i*2, 1); nlRightHandSide(xN); nlEnd(NL_ROW); } 

さて、システムの準備ができており、状態間の遷移に関する厳密なルールが設定されています。システムの品質の2次関数も設定されています。ボックスを振って、最小二乗が解x_i、u_iとして与えられることを確認しましょう（赤い線は速度、緑は加速度です）：



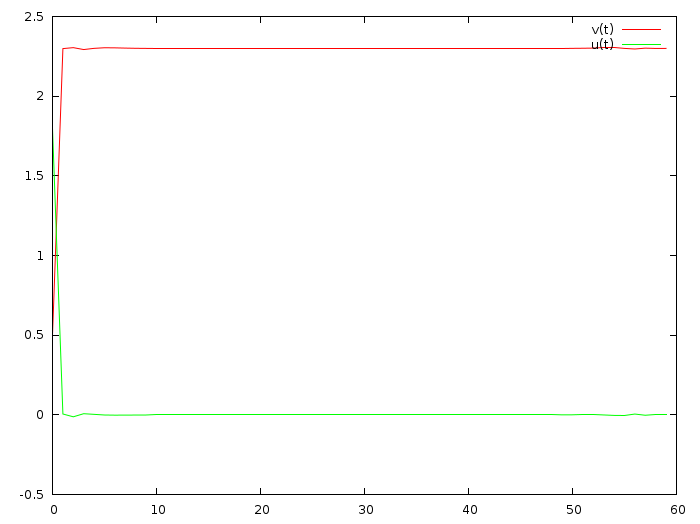
Oookey、実際には毎秒0.5メートルから毎秒3のコンマである2メートルに加速しましたが、私たちのシステムは過度に加速しました（できるだけ早く収束することを要求したため、これは論理的です）。

そして、最小の加速を求める最速の収束ではなく、目的関数を変更しましょう（ ここではcommitします ）：

  for (int i=0; i<N; i++) { nlBegin(NL_ROW); // ui = 0, soft nlCoefficient(i*2+1, 1); nlEnd(NL_ROW); } 

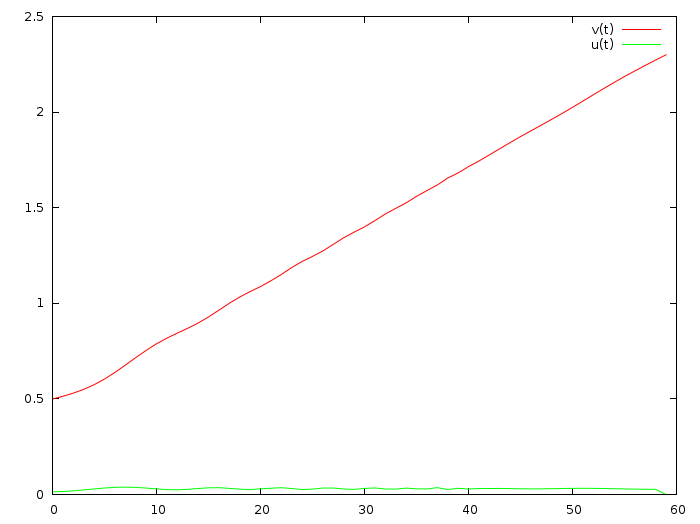
うーん、今では車は1分間に毎秒2メートル加速しています。 では、最終的な速度にすばやく収束させて、少し加速してみましょう（ ここがコミットです）。

  for (int i=0; i<N; i++) { nlBegin(NL_ROW); // ui = 0, soft nlCoefficient(i*2+1, 1); nlEnd(NL_ROW); nlBegin(NL_ROW); // xi = xN, soft nlCoefficient(i*2, 1); nlRightHandSide(xN); nlEnd(NL_ROW); } 

うん、すごい、今は美しくなっている：



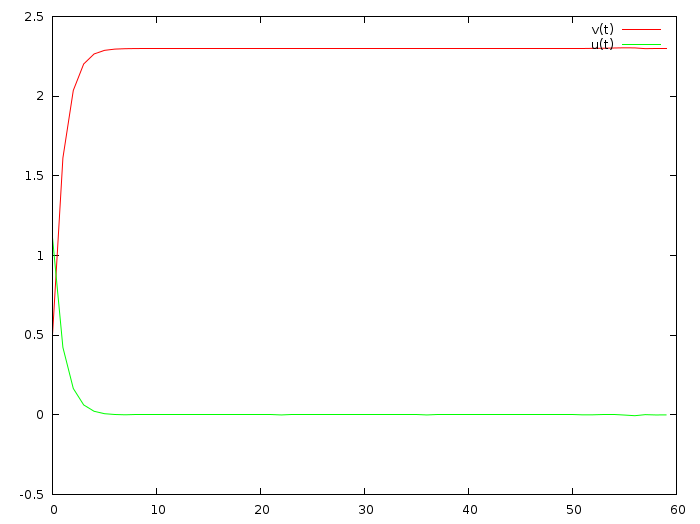
したがって、制御の大きさの高速収束と制限は、もちろん、競合する目標です。 Wikipediaの段落の最初の行で停止した時点で、ひどい数式があり、それらは理解できません。 多くの場合、記事を読むことは、キーワードを検索し、私が個人的に所有しているのと同じデバイスを使用してすべての結果を完全に表示することになります。

では、現時点では何がありますか？ システムの初期状態+システムの最終状態+秒数を持つことにより、理想的な制御u_iを見つけることができます。 これは、セグウェイがあまり適切でない場合にのみ有効です。 くそー、どうやってそれをやるの？ したがって、Wikipediaで次のテキストを読んでください。

次のように定義されたパフォーマンスインデックス



パフォーマンスインデックスを最小化する最適な制御シーケンスは、



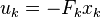
ここで[次は何ですか？！]

だから 「J = ...」という式の等号の後はわかりませんが、これは明らかに2次関数です。 目標への迅速な収束と最小コストのように、後で詳しく見ていきます。これで理解は十分です。

u_k = -F x_k。 おっと。 彼らは、私たちの1次元の例では、いつでも最適な加速度は定数-Fに現在の速度を掛けたものであると言っています。 さあ、さあ。 しかし、真実は、緑と赤のグラフィックが互いに疑わしいほど似ているということです！

1Dの例で実際の方程式を書いてみましょう。

そのため、品質管理機能があります。



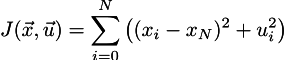
車の速度の隣接する値の間の接続の制限を観察しながら、それを最小化したい：



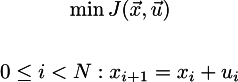
ストップ-ストップ-ストップですが、ウィキペディアのx_k ^ TQ x_kは一体何ですか？ 結局のところ、これは単純なx_k ^ 2であり、（x_k-x_N）^ 2？！ モミの木、しかし彼らは我々が入りたいと思う最終状態はゼロベクトルだと仮定します!!! [検閲済み]これについては、WIKIPEDIA全体のページに単語がありますか？！

さて、深く呼吸し、落ち着いてください。 ここで、制限がないように、u_iを介してJの定式化ですべてのx_iを表現します。 これで、制御ベクトルのみが変数になります。 そのため、次のように記述された関数Jを最小化します。



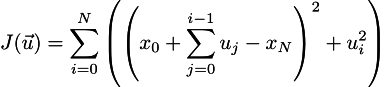
つまずく。 ブラケットを開きましょう（エピグラフを参照）：



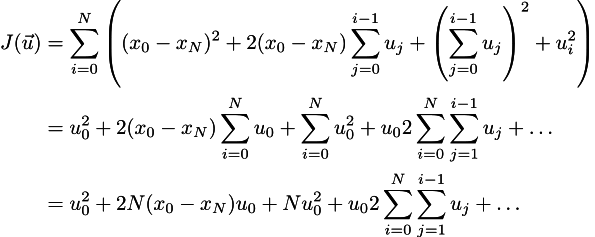
ここの省略記号は、u_0から独立しているかすを意味します。 最小値を探しているので、それを見つけるために、すべての偏微分をゼロに設定する必要がありますが、最初はu_0に関する偏微分に興味があります。



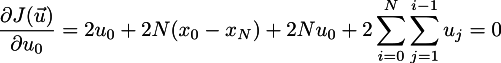
合計すると、u_0に次の式がある場合にのみ最適な制御が最適になることがわかります。



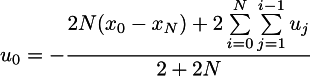
この式には他の不明なu_iも含まれますが、「but」が1つあることに注意してください。 冗談は、車が毎分2メートルしか加速しないようにすることです。 私が彼女に与えた分は、故意に十分な時間のようでした。 そして、私は1時間を与えることができます。 u_iに依存する用語は、失礼な場合、すべて加速の仕事であり、Nに依存しません。 したがって、Nが十分に大きい場合、最適なu_0は最終位置からx0がどれだけ離れているかにのみ線形的に依存します。

つまり、制御は次のようになります。システムをモデル化し、u_iとx_iを線形に接続するマジック係数を見つけて記述し、ロボットで、見つかったマジック係数を使用して線形比例コントローラーを作成します。


非常に正直に言うと、この時点まではもちろん、コードを書くことはしませんでした。私は心の中で上記のすべてを行い、一枚の紙に少し書きました。 しかし、これは私が一度だけ多くのコードを書くという事実を否定するものではありません。

2Dの例

直観として、これは素晴らしいですが、 ここに私が実際に書いた最初のコードがあります ：


ここではすべてが同じで、システム変数のみが2つになりました。速度だけでなく、マシンの座標も2つです。
したがって、初期位置+初期速度（x0、v0）が与えられると、最終位置（0,0）に到達し、原点で停止する必要があります。
ある瞬間から次の瞬間への遷移は、x_ {k + 1} = x_k + v_k、およびv_ {k + 1} = v_k + u_kとして実行されます。

私は以前のコードについて十分にコメントしましたが、これは問題を引き起こさないはずです。 作業の結果は次のとおりです。



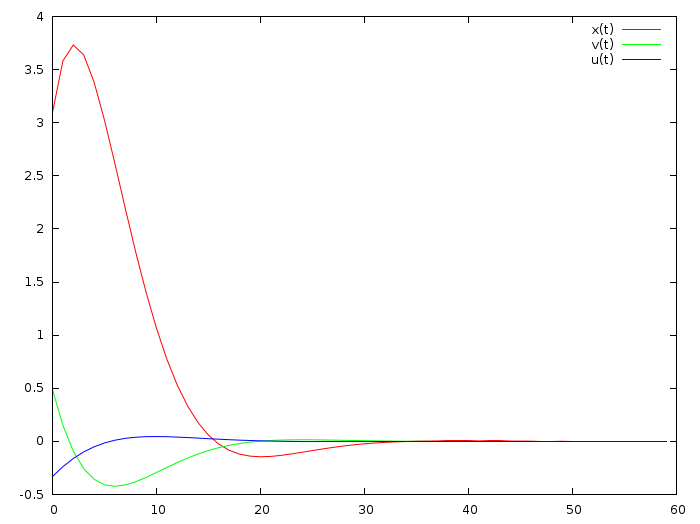
赤い線は座標、緑は速度、青はアクセルペダルの位置です。 前のものに基づいて、青い曲線は赤と緑の加重和であると想定されます。 うーん、そうですか？ 数えてみよう！
つまり、理論的には、u_i = a * x_i + b * v_iのような2つの数値aとbを見つける必要があります。 そして、これは前回の記事で行った線形回帰にすぎません！ これがコードです。

その中で、最初に上の図にある曲線を検討し、次に青い曲線= a *赤+ b *緑になるようにaとbを探します。

ここに、実際のu_iと、緑と赤の線を折りたたんで得たものとの違いを示します。


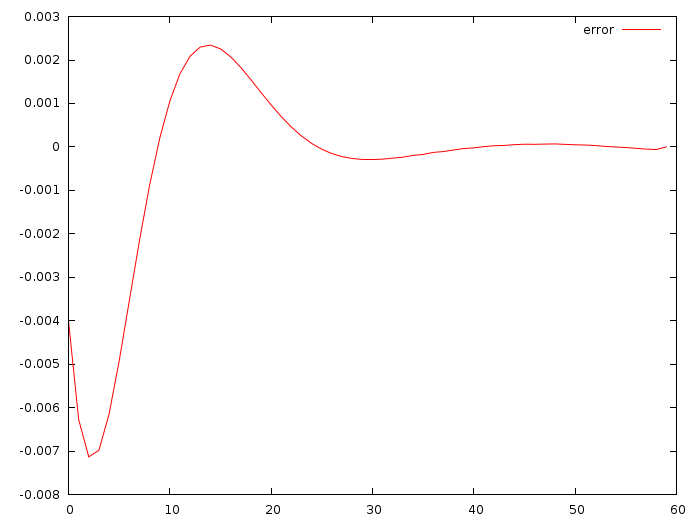
1秒あたり1秒あたり100分の1メートルのオーダーの偏差！ かっこいい!!! 私が引用したコミットは、a = -0.0513868、b = -0.347324を提供します。 偏差は本当に小さいですが、これは正常です。初期データは変更しませんでした。

それでは 、マシンの初期位置と速度を根本的に変更して、以前の計算からマジック番号aとbを残してみましょう。

この最適なソリューションと、最も愚かな手順で得られるものとの違いを次に示します。もう一度完全に説明します。

  double xi = x0; double vi = v0; for (int i=0; i<N; i++) { double ui = xi*a + vi*b; xi = xi + vi; vi = vi + ui; std::cout << (ui-solution[i*3+2]) << std::endl; } 

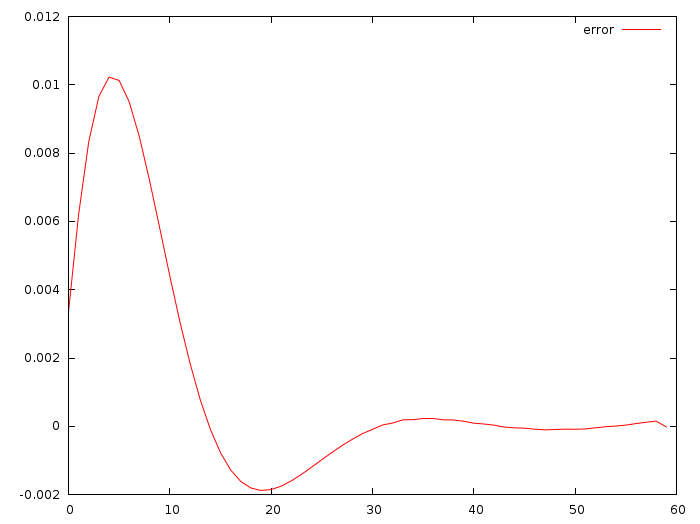
ウィキペディアが提供してくれたリカッチ微分方程式はありません。 私も彼らについて読む必要があるかもしれませんが、彼らが料理するとき、それは後であります。 それまでの間、単純な2次関数は私を完全に満足させます。

乾燥残渣

合計：これを使用するには、主に2つの困難があります。
a）良好な遷移行列AおよびBを見つけます。もちろん、すべてがオブジェクトや他のものの質量に依存するため、運動方程式を記述する必要があります。
b）目標への最速の収束の目標間の適切な妥協係数を見つけますが、同時に余分な努力をすることはありません。

aとbが完了すると、メソッドは有望に見えます。 唯一のことは、システムの状態に関する完全な知識を必要とすることであり、常に機能するとは限りません。 たとえば、セグウェイの位置はわかりません。ジャイロスコープや加速度計などのセンサーのデータに基づいて推測することしかできません。 ええ、これはそれについてです。次回は生徒に教えます。

だから、私は3つの目標を達成したかった：
a）lqrとは何かを理解する
b）私が理解したことを生徒とあなたに説明する
c）あなたと私の生徒に、私（ほとんどの人がそうであるように）数学のテキストでは気の毒なことを理解していないことを示します。 私たちは、しがみつくキーワードを探し、冗長で不必要な方法と抽象化を捨て、現在の知識の範囲内に押し込もうとしています。

私は成功したと思います。 繰り返しになりますが、私は制御理論の専門家ではありません。補足や修正が必要な場合は、恥ずかしがらないでください。

お楽しみください！