
次の「C ++キラー言語」から抜け出し、いくつかのNoSQL DBMSの見事な合成パフォーマンステスト、新しいJSフレームワークの誇大広告、そして「プログラミングのためのプログラミング」の世界に飛び込みましょう。
まえがき
私にとって3月は、Habrはもはや ケーキではないという事実に関する記事を読むことから始まりました。 回答から判断すると、このトピックは痛いほど明らかになった。 一方、私はこれから自分自身のために何かを学べました。 「あなたはレジスタンスです」 あなたがそれを読んだ場合-あなたはHabrです。 そして、それをもっと面白くする(または、少なくとも多様化して、広告投稿、アバウトエリザリズム、企業ブログの集約という新しいトレンドから離れること)は、一般ユーザーのみが可能です。 当時は小さなプロジェクトでしたが、深刻な修正が必要だったので、話したいと思いました。 そして、私は決めました-1か月後に( 素朴です! )記事を書きます。 ご覧のとおり、今 真ん中 4月の終わり 5月上旬 5月は本格的で、あなたは私の怠と自由時間の不規則性の両方を責めることができます。 しかし、それでも記事は光を見ました! おもしろいのは、この記事の執筆中に、2つの類似したものがすでに出てきたことです: 文法の進化と簡単な実装 、 シンボリック回帰とは別のアプローチです。 私がそのようなスロポックでなかったなら、あなたは1ヶ月の遺伝的アルゴリズムに適合して宣言することができました:)
はい、2016年がヤードにあることを完全に認識しており、このような長い投稿を書いています。 また、図面が作成されます 「鶏の足」のスタイルで フォント付きのタブレット上のペン オタクのための漫画サン xkcd
はじめに
少し前に、興味深い記事がGTに登場しました。これは特徴的で、 さらに興味深いコメントです(そして、自然選択についてはどのような言葉の戦いがありましたか!)。 プログラミングで自然選択の原則を適用すると(より正確には、 メタプログラミングで )アイデアがありましたか? あなたが推測できるように、この考えは最終的に遺伝的アルゴリズムの長い間存在する概念を再発見することにつながりました。 材料の簡単な研究、私は熱心に実験に駆けつけました。
しかし、すべてについて順番に話しましょう。
教育プログラム
遺伝的アルゴリズムの根底にあるほぼすべての原則は、 自然選択から引き出されます。環境変化を通じて人口が適応し、それらの中で最も適応したものが支配的になります。
遺伝的アルゴリズムを使用して問題を解決する方法は? すべてがゼロ次近似で単純に機能することに驚かれることでしょう。
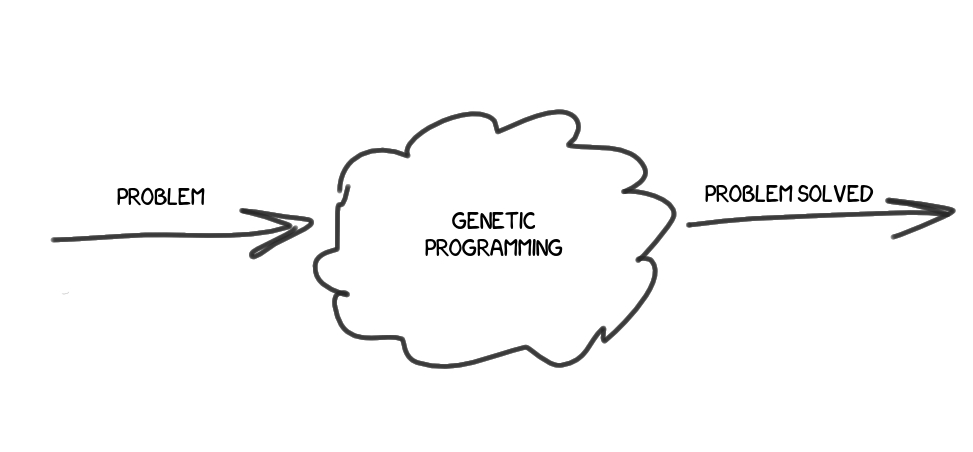
今、 我々はより深く行く必要があります。 最初の近似:
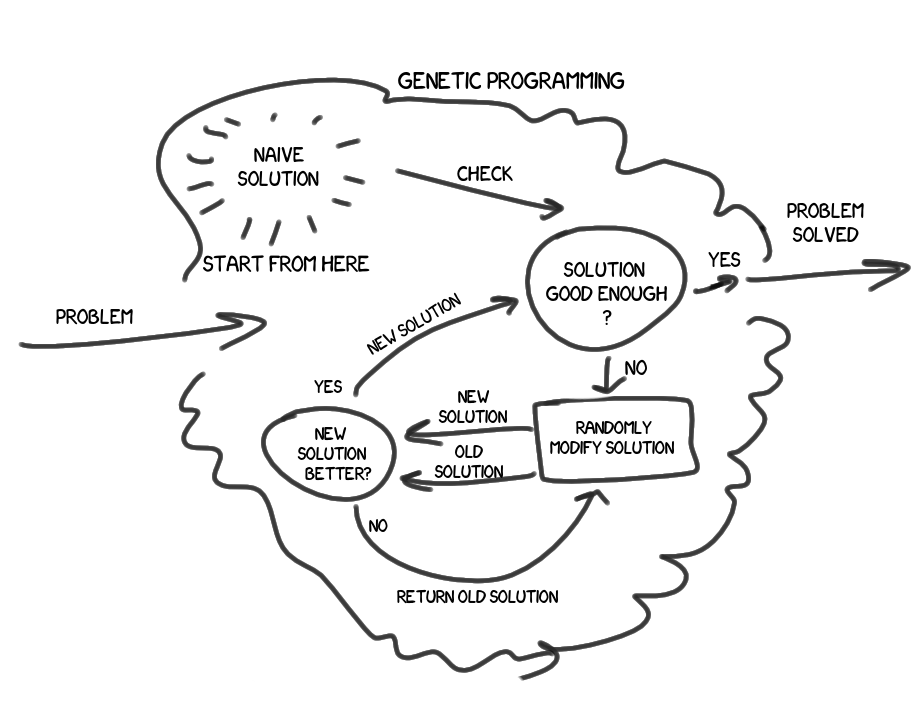
だから、私たちには問題/問題があります、それに対する解決策を見つけたいのです。 基本的で貧弱で素朴な解決策がいくつかありますが、その結果はおそらく満足できません。 このソリューションのアルゴリズムを使用して、わずかに変更します。 問題の本質を理解することなく、分析なしで自然にランダムに。 新しいソリューションは結果をさらに良くしましたか? そうでない場合は、破棄して、もう一度繰り返します。 はいの場合- 乾杯 ! 新しいソリューションの結果は完全に満足していますか? もしそうなら、我々は素晴らしい、与えられた精度で問題を解決した。 そうでない場合は、結果のソリューションを取得し、同じ操作を実行します。
ここに、最初の近似としてのアイデアの簡潔で単純な説明があります。 しかし、それは探究心を満足させるものではないと思います。
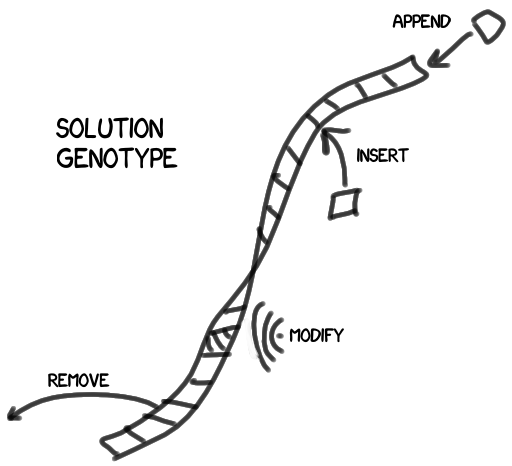
まず、ソリューションを変更するにはどうすればよいですか?
私たちのソリューションは、特性、または必要に応じて遺伝子である一連の個別のブロックで構成されています。 セットを変更すると、決定が変更され、結果が改善または悪化します。 私は遺伝子型を遺伝子の連鎖として描写しましたが、実際にはツリー構造になります(ただし、ノードの1つに連鎖を含めることはできません)。
次に、メインループを詳しく見てみましょう。
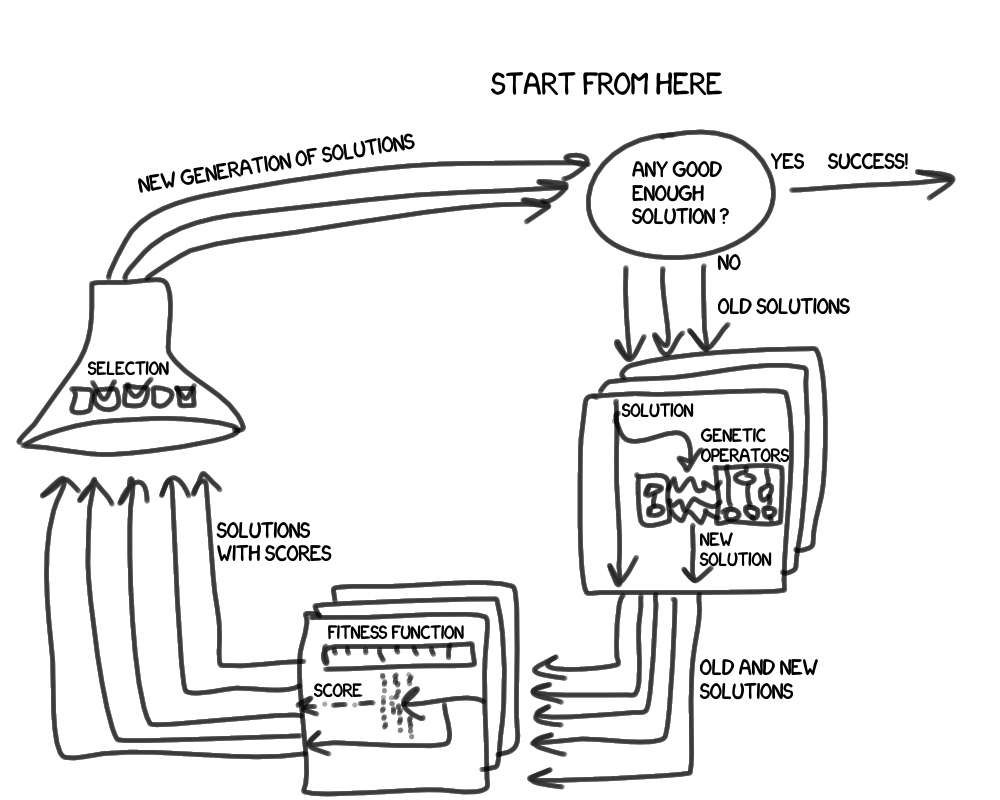
2番目の近似で何が識別可能になりましたか? まず、私たちは1つではなく、ソリューションのグループで動作します。これを世代と呼びます。 第二に、新しいエンティティが登場しました:
- 遺伝的操作 (はい、翻訳との永遠の混乱、英語の「 演算子 」は私たちの「 操作 」です)は、以前のものに基づいた新しいソリューションを得るために必要です。 通常、これはクロス (2つの異なるソリューションのランダムな組み合わせ)と突然変異 (1つのソリューションのランダムな変更)です。
- 決定の結果に対する満足度を評価するには、 フィットネス関数 ( フィットネス関数の方が好き)が必要です。
TDDは誰の頭に浮かびますか?実際に いつ コードがテストに失敗したかどうかの質問に答えるだけでなく、 成功にどれだけ近づいたかの測定可能な評価を与えるテストを簡単に書く方法を学ぶなら、私たちは自己記述プログラムに一歩近づきます。 そのような試みが既に行われている場合、私は驚かないでしょう。
- この選択は、次世代の意思決定の原則を説明しています。
欠点
どんなに有望なものでも、問題を解決するための議論されたアプローチは完全です 致命的 基本的な欠陥。 実際には、おそらく、すべての既知の落とし穴についてつまずいた。 私の意見では、最も重要なのはスケーラビリティの低さです。 平均的な計算コストの増加率は、入力データの増加率を上回ります(単純なソートアルゴリズムの場合と同様)。 残りの欠点については、さらに詳しく説明します。
練習する
言語選択
Rubyが選択されました。 この言語は、Pythonが伝統的に占領していた私の問題のニッチを埋めてくれました。 そして、ここにそのような機会があります! 私は一度にN ( N > 1)匹のウサギを殺すのが好きです。 私のコードは、古いルビストの顔面掌紋ではないにしても、時々笑顔を引き起こす可能性があることを除外しません(いいえ、申し訳ありませんが、それはルビストです、他のオプションはトローリングです)。
遺伝子型
最初の考えは、言語がevalを取得すると、任意の文字(遺伝子として動作)からトリックなしでソリューションの遺伝子型を構築でき、最後にRuby自身が解釈するスクリプトを作成できるというものでした。 2番目の考えは、このような高い自由度を持つ決定の進化には、本当に何年もかかる可能性があるということでした。 ですから、私は指をこの方向に動かすことすらしませんでした。 ムーアの法則が守られていれば、約30年でこのアプローチを試すことができます。
最後の進化は、かなりタイトなフレームワークに囲まれていました。 ソリューション遺伝子は高度に組織化されたトークンであり、ネスト(ツリー構造の構築)の可能性があります。
数式としてのソリューションについて説明する最初の実験では、トークンは定数、変数、およびバイナリ演算です(プロジェクトの文脈では、「バイナリ演算」とは2つのオペランドに対するアクション、つまり加算を意味します)。
ところで、私はevalとの互換性を部分的に残すことにしたので、トークンの文字列表現を(標準のto_sを介して)要求すると、解釈のために完全に消化可能な文字列を取得できます。 例:
f = Formula::AdditionOperator.new(Formula::Variable.new(:x), Formula::IntConstant.new(5)) f.to_s
はい、より明確に。
遺伝子操作
ソリューションの遺伝子型を変更する唯一の主要な方法として、 突然変異を選択しました。 主に、より形式化されているからです。 私は交配による繁殖がより効果的であることを除外しません(そして野生生物の例から判断すると、そうです)が、その形式化には多くの落とし穴があり、おそらく、遺伝子型の構造そのものに特定の制限が課せられます。 一般的に、私は簡単な方法で行った。
最終実験の説明に当てられた記事のセクションでは、ソリューションの突然変異の規則が詳細に説明されています。 しかし、私が話したい一般的な機能があります:
- 時々(実際にはしばしば)、突然変異は一般に正しい方向であるにもかかわらず、突然変異のほんの1ステップで改善された結果を達成することが不可能であることが起こります。 したがって、遺伝的操作を適用する段階では、ソリューションは1ターンあたり無制限の回数の突然変異を許可されます。 確率は次のようになります。
-50%-1つの突然変異
-25%-2つの突然変異
-12.5%-3つの突然変異
-など - いくつかのステップで、突然変異体が親と同一になるか、異なる親が同じ突然変異体を取得することがあります。 そのような場合は抑制されます。 さらに、私は一般的に、1世代のフレームワーク内でソリューションの厳密な一意性を維持することにしました。
- 突然変異によって、完全に機能しない解決策が生じることもあります。 これに対処することは分析的に非常に困難です。通常、問題はフィットネス関数による評価時にのみ明らかになります。 私はそのような決定をさせます。 とにかく、ほとんどは繁殖の結果として消えます。
フィットネス機能
その実装には問題はありませんが、1つの注意点があります。フィットネス関数の複雑さは、解決される問題の複雑さの増加とほぼ同程度に増加します。 彼女が合理的な時間で彼女の仕事を行えるようにするために、私はそれを可能な限り簡単に実装しようとしました。
生成されたソリューションは、入力データの特定のセットに基づいて特定の結果を返すことを思い出させてください。 したがって、特定の入力データのセットに対して取得する必要のある理想的な( 参照 )結果を知っていることが暗示されます。 結果は定量化できます 。つまり、返された結果を参照と比較することにより、特定のソリューションの品質を定量化できます 。
さらに、各ソリューションには間接的な特性があり、その中から、主なものとしてリソースの集中度を特定しました。 一部のタスクでは、ソリューションのリソース消費は入力データのセットに依存していますが、他のタスクでは依存していません。
トータルフィットネス機能:
- 解の結果が参照とどのように異なるかを計算します
- ソリューションのリソース集約度を決定します
リソースの強度について初期のプロトタイプでは、テストの合格に費やされたプロセッサー時間を測定しようとしましたが、長時間(数十ミリ秒)の実行でも、オペレーティングシステムによって作成された同じソリューションの時間の±10%の広がりがあり、定期的な排出量は+ 100-200%でした。
そのため、最初の実験では、リソース消費量は遺伝子型の総複雑度によって計算され、2回目の実験では実際に実行されたコード命令の計算が行われます
育種
各世代には、 N個以下のソリューションが含まれます。 遺伝演算子を適用すると、最大2N個のソリューションが得られます。さらに、次世代では、 N個を超えることはできません。
次世代のソリューションはどのような原理で形成されますか? 各ソリューションがすでにフィットネス関数の評価を受けている段階にあります。 もちろん、見積もりは相互に比較できます。 したがって、現在の世代のソリューションをソートできます。 さらに、単にXのベストソリューションを採用し、それらから次世代を形成することは論理的に思えます。 しかし 、私はこれにこだわることはせず、新世代には残りのYランダム解も含めることにしました。
たとえば、 X = Yの場合、次の世代に決定を渡すために、彼は最高の25%であるか、3面体キューブ(存在する場合)で3をロールする必要があります。 人道的に十分な条件ですか?
そのため、種の多様性を維持するには、次世代に偶然の生存者を含める必要があります。 事実、長い間、相互に類似し、最良のものの中にとどまるソリューションは残りを絞り出し、さらに先に進むとプロセスが速くなり、支配的なブランチがデッドロックすることがよくあります。
パラメータXとYは 、もちろんカスタマイズ可能です。 ランダム生存者とランダム生存者の両方でテストを実行し、それらをアルゴリズムに追加することの妥当性を証明しました:場合によって(複雑性が増したソリューションを検索するとき)、それらを使用してより良い結果を達成することができました(さらに、ソリューションの検索に費やされた総力は残りました定数、たとえば、 X 1 = 250、 Y 1 = 750対X 2 = 1000、 Y 2 = 0)。
勝利条件
ここに障害があります:終了する時だということをどのように理解するのですか? ソリューションが結果の精度で私たちを満足させると仮定しますが、複雑さはどうでしょうか? 突然、アルゴリズムが動作し、 O(n)のグラフを着色するためのソリューションが生成されますか? もちろん誇張しますが、仕事を止めるための基準は形式化されなければなりません。 私の実装では、 トップ1ソリューションが特定の世代数( R-ラウンドと省略)を変更しない場合、アルゴリズムの実行が終了します。 ローテーションがないということは、まず、現在の最適なソリューションを超える代替ソリューションがなかったことを意味します。 第二に、現在の最良の解決策では、一定期間、それ自体の改善された突然変異を生成できませんでした。 最適なソリューションの勝利につながる世代の数、通常は多数-進化がそれ以上進められないことを本当に確認するには、数百(数はタスク自体の複雑さによって異なります)世代が必要です。
残念ながら、多くの予防策にもかかわらず、進化が行き詰まる場合があります。 これは遺伝的アルゴリズムのよく知られた問題であり、ソリューションの主な集団が局所的な最適化に焦点を合わせ、最終的には望ましいグローバルな 最適化を無視します。 これは、勝者のクォータの減少、ランダムのクォータの増加、勝利の支配時間の増加、独立した世代の並列化のパラメーターを使用してゲームで答えることができます。 しかし、これにはすべて電力と時間が必要です。
具体的な実装
いつものように、すべてはgithubに配置されます(これまでのところ、ドックはありません)。
今、私に具体的に表示されるものについて 自転車 実装:
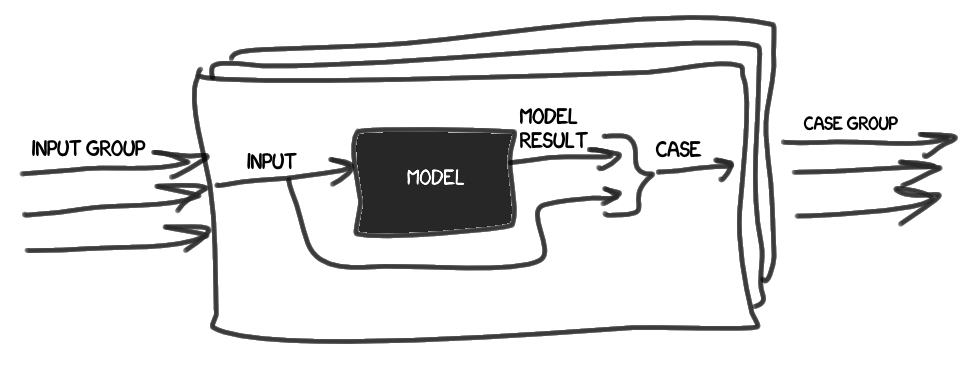
- モデルの概念が導入されました。 入力データのセット(入力)に基づいて、 参照結果 (モデル結果)を取得できるブラックボックスと見なします。
- ケースには、一連の入力データと参照結果が含まれています。
一連の入力データ(入力グループ)に基づいて、ケースグループ(ケースグループ)を収集します。
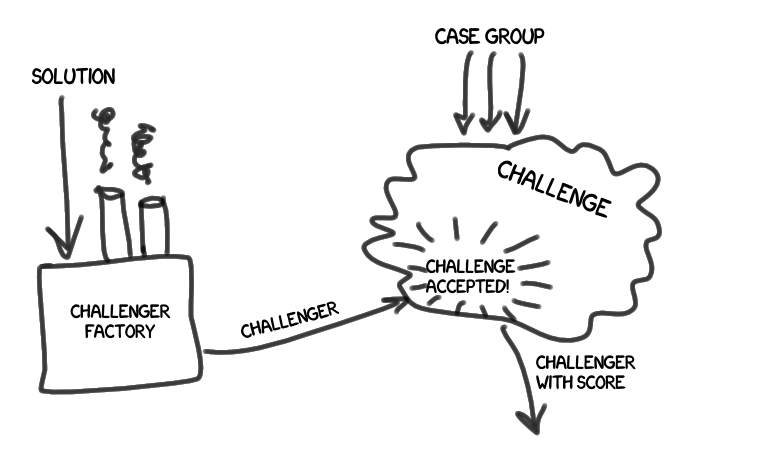
- チャレンジ(またはテスト )(チャレンジ)は、以前に形成された一連のケースを通過するための一連のアクションです。 テストの肩には、 合格の結果を評価し、成績を比較する作業もあります。
特定のソリューション(ソリューション)を持っている申請者 (チャレンジャー)がいます。 申請者は秘跡の「 挑戦を受け入れました! 」と発音し、自分の適合性の程度を学びます(スコア)。
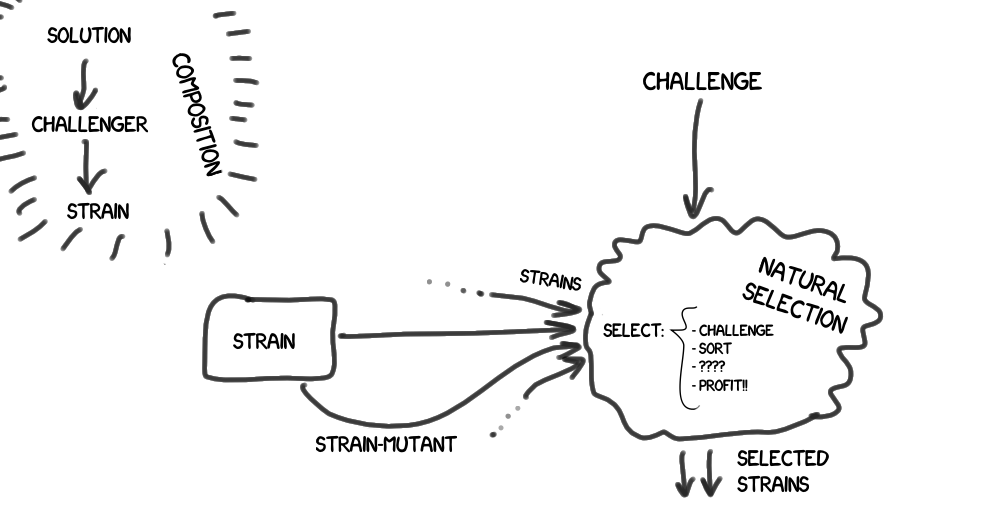
- その結果、構成チェーンを並べます- 解決策 (解決策-特定の種類の問題に対する解決策を提供します)-> 申請者 (挑戦者 - テストに合格します )-> ひずみ (ひずみ- 自然選択と進化に参加します(以下を参照))
testを含む自然選択 (Natural Selection)があり、指定されたルールに従って、それに到達する株のグループをフィルターします。
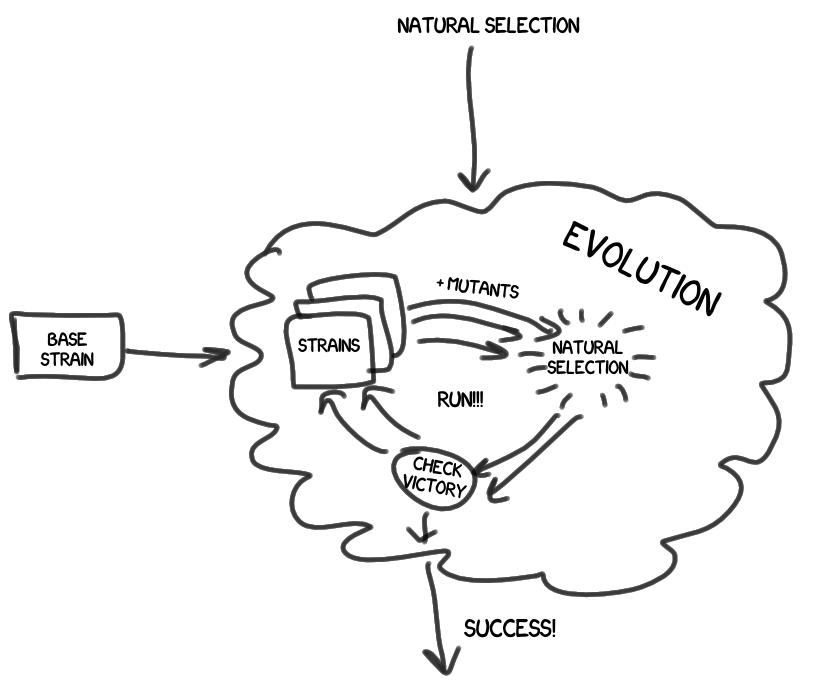
- 上のレベルには進化があり、 自然選択を含め、株のライフサイクル全体を支配します。
- 進化の仕事の結果は勝利の緊張であり、それを英雄として尊敬し、そして彼の家系図を含めて注意深く研究します。 そして、結論を導き出します。
これは、一般的に言えば、遺伝的アルゴリズムの私の実装です。 抽象クラス( Rubyの huh> _ <)により、特定のタスク領域から一般的に独立したコードを書くことができました。
後続の実験では、必要な入力、モデル、ソリューション、スコア (もちろん多く)が追加されました。
一般的に、 実験1:算術式を呼び出す方がより正確ですが、 式の基本クラスの名前を選択したとき、二度考えずにFormulaに決め、この記事の残りの部分では算術式formulasを呼び出します 。 この実験では、1つ以上の変数を含む標準の数式 (同じModel )を導入します。 例:
x 2-8 * x + 2.5
たとえば、変数値のセット( 入力グループ 、ええ)があります。
- xは0です。
- xは1です。
- x = 2;
- ....
- x = 255;
標準と比較するソリューションは同じ式ですが、それらはランダムに作成されます-基本式から順番に変化します(通常はx )。 ソリューションの品質の評価( スコア )は、 標準の結果からの結果の平均偏差に加えて、ソリューションのリソース消費量(操作の総重量と式の引数)です。
前述のように、式トークンは定数、変数、および二項演算です。
数式はどのように変化しますか? 数式に含まれるトークンの 1つに影響し、次の3つの方法があります。
- 成長 -成長、合併症
- 縮小 -削減、簡素化
- シフト -条件付き複雑さによる変更
さまざまな種類の突然変異に対するさまざまな種類の式で何が起こるかを以下の表に示します。
| 数式→突然変異↓ | 定数 | 可変 | バイナリ演算 |
|---|
| 成長する | 変数になるか、新しいランダム2項演算に含まれます(ランダムな第2オペランドを使用) | (ランダムな第2オペランドを使用した)新しいランダムなバイナリ演算へ | (ランダムな第2オペランドを使用して)新しいランダムなバイナリ演算で結合します |
| 縮む | 削減できないため、 シフト操作を適用します | 定数になる | 操作の代わりに、オペランドの1つだけが残ります |
| シフト | 値をランダムな値に変更し、タイプを変更できます(Float <-> Int) | 別のランダム変数になります(このコンテキストで適切な場合) | オペランドが交換されているか、操作のタイプが変更されているか、操作を削減しようとしている |
注1 数式の略語は、可能な場合は事前に定数の演算を実行しようとする試みです。 たとえば、 " (3+2) " get " 5 "、および " 8/(x/2) " get " (16/x) "から。 タスクは予想外に非常に自明ではないことが判明したため、徹底的な単体テストで ソリューションのプロトタイプを書くことを余儀なくされ、その後、深さから削減するための定数を引き出して本当の再帰的なソリューションを得ることはできませんでした。 これを理解することはエキサイティングでしたが、ある時点で、私は主要なタスクからあまりにも逸脱していたので、自分自身を止めて、到達した解決策にとどまる必要がありました。 ほとんどの場合、削減はすでに完全に機能しています。
注2演算には他の式、ネストされたオペランドがあるという事実により、2項演算の突然変異には特異性があります。 操作とオペランドの両方を変更することは、1つのステップに対して大きすぎる変更です。 したがって、ランダムに決定されるイベントは次のとおりです。20%の確率でバイナリ演算自体が変化し、40%の確率で第1オペランドが変化し、残りの40%の確率で第2オペランドが変化します。 20-40-40の比率が理想的であるとは言えません。おそらく、操作の突然変異確率の相関関係はそれらの重み (実際には、ネストの深さ)に応じて導入されるべきですが、今のところうまくいきます。
結果
さて、実際のところ、すべては次のとおりでした。
最初の参照は単純な多項式です:
x 2-8 * x + 2.5
Xは、0から255までの値を1ずつ増やします
R = 64、 X = 128、 Y = 128
実行は3回実行され、3つの結果のうち最良の結果がここに表示されます。 (通常、3回とも同じ結果が得られますが、突然変異が停止し、与えられた精度を達成することすらできないことがあります)
結果はまさに私を驚かせました:) 230世代以上( トップ1が変化しなかったR時間を含む)、次の解決策が導き出されました:
(-13.500 +((x-4) 2 ))
完全な血統覚えているように、1世代から複数の突然変異までが許可されています。
x (x-0) ((x-0)-0.050) (0.050-(x-0)) (0.050-(x-1)) (x-1) (x-1.000) ((x-1.000)--0.010) ((x-1.000)-0) ((x-1.000)-(1*0.005)) ((x-1.000)/(1*0.005)) ((x-1.020)/(1*0.005)) ((x-1.020)/(0.005*1)) ((x**1.020)/(0.005*1)) ((x**1)/(0.005*1)) ((x**1)/(0.005*(0.005+1))) ((x**1)/(0.005*(0.005+1.000))) (x**2) ((x--0.079)**2) ((x-0)**2.000) (((x-0)**2.000)/1) (((x-0)**2)/1) ((((x-0)**2)-0)/1) (((x-0)**2)-0) (((x-0)**2)-0.000) (((x-(0--1))**2)-0.000) (((x-(0--2))**2)-0.000) (((x-(0--2))**2)+0.000) (((x-((0--2)--1))**2)+0.000) (((x-((0--2)--1))**2)+-0.015) (((x-((0--2)--1))**2)+0) ((-0.057+0)+((x-((0--2)--1))**2.000)) ((-0.057+0)+((x-3)**2.000)) (((-0.057+0)**-1)+((x-3)**2.000)) (((-0.057+0)**-1)+((x-4)**2.000)) (((-0.057+0)**-1.000)+((x-4)**2.000)) (((-0.057+0.000)**-1.000)+((x-4)**2.000)) (((x-4)**2.000)+((-0.057+0.000)**-1.000)) (((x-4)**2)+((-0.057+0.000)**-1.000)) (((x-4)**2)+((-0.057+0.000)**-0.919)) ((((x-4)**2)+((-0.057+0.000)**-0.919))+-0.048) ((((-0.057+0.000)**-0.919)+((x-4)**2))+-0.048) ((((-0.057+0.000)**-0.919)+((x-4)**2))+-0.037) (((-0.057**-0.919)+((x-4)**2))+-0.037) (-0.037+((-0.057**-0.919)+((x-4)**2))) (-13.524+((x-4)**2)) (-13.500+((x-4)**2))
つまり、計算の結果が最終的に参照のものと一致し始めた後、彼はリソースの強度を追求し、変換を実行しました。その結果、自然選択に基づく式がコンパクトに勝ちました!
実際、間違ってそのような結果を受け取ったのは不思議です。 最初の実行では、別の変数xが追加された突然変異のタイプが禁止されていました。 奇妙なことに、完全な突然変異よりもさらにうまく機能しました。 バグが修正されたときの結果は次のとおりです。
- R = 250、 X = 250、 Y = 750、精度= 0.001、(結果の重み 49)
(2.500 +((x-8)* x))
- R = 250、 X = 1000、 Y = 0、精度= 0.001、(結果の重み 60)
(((x-1)*(-7 + x))-4.500)
この場合、ランダムなものにクォータを設定したオプションは1回失敗しましたが、2番目のオプションよりも最適な結果を得ることができました。 ここで、結果の最適値への近似ごとに、基本的に1つの突然変異ステップで十分です。 次の場合、すべてがそれほど単純ではありません!
2番目の標準は自然対数です。
ln(1 + x)
xは0から25.5までの値を0.1単位で取ります
私たちのソリューションは対数を直接使用する機会を奪われていますが、この標準はテイラー級数で拡張されています:
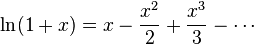
それでは、ソリューションが与えられた精度でそのようなシリーズを再現できるかどうか見てみましょう。
最初は0.001の精度で実行しようとしましたが、数日間のアルゴリズムのハードワークの後、解はわずか0.0016の精度に達し、式のサイズは1000文字になる傾向があったため、精度バーを0.01に下げることにしました。 結果は次のとおりです。
- R = 250、 X = 250、 Y = 750、精度= 0.01、(結果の重量 149)
(((((-1.776-x)/19.717)+(((x * x)-0.318)** 0.238))-(0.066 /(x + 0.136))))
- R = 250、 X = 1000、 Y = 0、精度= 0.01、(結果の重み 174)
(((-0.025 * x)+(((x * x)** 0.106)** 2))/(1+(0.849 /((x * x)+1))))
ご覧のように、この標準にランダムな生存者を含める場合、指定された精度を維持しながら、リソースをあまり使用しないソリューションが見つかりました。 テイラーシリーズによく似ているわけではありませんが、本当だと思います:)
3番目の標準は、ラジアンで指定された正弦です。
罪(x)
xは、0.02の増分で、0〜6.28の値を取ります。
繰り返しますが、標準はテイラー級数に拡張されます。
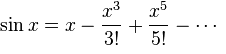
この場合、 xの結果が-1から1の値を取ることを考えると、0.01の判定精度はより深刻なテストでしたが、アルゴリズムはそれを行いました。
- R = 250、 X = 250、 Y = 750、精度= 0.01(結果の重み 233)
(((((-0.092 ** x)/2.395)+((((-1.179 **((((x-1)* 0.070)+-0.016)* 4.149))-(0.253 ** x))+ 0.184 ))**(0.944-(x / -87))))
- R = 250、 X = 1000、 Y = 0、精度= 0.01、(結果の重み 564)
(((x + x)*((x * -0.082)**(x + x)))+(((x + x)**(0.073 ** x))*((((1-(- 0.133 * x))*(-1-x))*((x / -1)*(-0.090 **(x-0.184))))+(((((--1.120+(x *(( x + 1)*-0.016)))**(-0.046 /((0.045 + x)**-1.928)))+(-0.164-(0.172 ** x)))* 1.357)** 0.881)) )))
繰り返しになりますが、標準の複雑さが増しているため、最良の結果は、ランダムなソリューションのプールを持つアルゴリズムのバージョンによって達成されました。
4番目の標準は、4つの(偶然?私は考えない)変数を持つ式です:
2 * v + 3 * x-4 * y + 5 * z-6
各変数は、0から3までの値を1ずつ増やし、合計256の組み合わせを取ります。
- R = 250、 X = 250、 Y = 750、精度= 0.01、(結果の重み 254)
((y * 0.155)+(-2.166 +(((((((z * 4)-(((y-(x +(y / -0.931))* 2)+-0.105))+((v +(v -2))+-0.947))+ x)+(z + -1))))
- R = 250、 X = 1000、 Y = 0、精度= 0.01、(結果の重み 237)
((-3+(v + z))+(((v +((xy)+((((z + z)-(((0.028-z)-x)+(y + y)))-y )+ z)))+ x)+-2.963))
私の期待に反して、最初の標準に比べて複雑さが非常に深刻になりました。 標準は複雑ではないようです。ソリューションを段階的に静かに増やして、結果を必要なものに近づけることができます。 しかし、0.001の精度は決してマスターされませんでした! ここで、私たちのアプローチにおけるタスクのスケーリングに関する問題は深刻であると疑い始めました。
まとめ
一般的に、私は得られた結果、特に標準2と3に満足していませんでした。その結果、厄介な式を推測するのに数千世代が必要でした。 これが起こる理由は3つあります。
- 不完全なリダクションメカニズム-たとえば、ブラケットとブラケットのより先見の明な開示が欠けています。 このため、式を便利な形にすることはできません。
- 自発的な突然変異が多すぎ、式が大きいほど、正しく開発される可能性は低くなります。 条件付きですべての可能な突然変異体のグループがオリジナルに基づいて形成され、事前選択が実行されるときに、「徹底的な」突然変異メカニズムを作成することを考えていました。 手が推測に到達するかどうか、およびこれがアルゴリズムを改善するかどうかはまだ不明です。
- 複雑な問題の解決策を見つけるためのこのような方法の基本的な非実用性。 おそらく、このアプローチは、 サルの軍隊によるタイプライターとの戦争と平和を書き込もうとすることから、これまでのところ行っていません。 おそらく、分析アプローチの必要性である複雑さは、そのようなタスクの自然で不可欠な特性です。
好奇心10年前にデータ圧縮に興味を持っていたことを思い出し、自分で決断を下すことに挑戦しました。 私は、それらが私を啓発するまで、ランダムなパターンを圧縮することができなかったことを嘆きました:)たぶんここにも?
さらなる実験
, .
, (, , ) ( , "" ""), , .
— . . , : - , , .
, ? . , , ? ,
nil
— ? .
, , , — , . , - .
, .
. !