モンテカルロ法は、人工知能の基礎としてゲームでよく使用される意思決定アルゴリズムです。 彼はGoをプレイするプログラムに強い影響を与えましたが、デスクトップと通常のコンピューターの両方の他のゲーム（例えば
Total War：Rome II ）でもアプリケーションを見つけました。 モンテカルロ法が絶賛されたAlphaGoプログラムで使用されていることも注目に値します。AlphaGoプログラムは、5回連続で第9段ゴープロのリーセドルを破りました。
この記事では、Trees（UCT）に適用されるUpper Confidence boundと呼ばれるバージョンのMonte Carloアルゴリズムについてお話したいと思います。 2006年にこのアルゴリズムが公開された後、Goをプレイするためのプログラムは位置を大幅に強化し、人間とのゲームで大きな成功を収めました。
UCTアルゴリズムの基礎は、多腕バンディットの問題を解決することです。 特に、Upper-Confidence-Bound（UCB）アルゴリズムが使用されます。 ここではすでにハブについて説明しましたが、それでも主なポイントを繰り返します。
タスクは次のとおりです。スロットマシンのセットがあり、それぞれが勝つ可能性があります。 最大のゲインをもたらすマシンを決定する必要があります。
UCBアルゴリズム：
1.初期化。 各マシンで1回プレイする
2.後続の各反復で、最大値を持つマシンを選択します
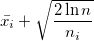どこで 
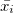これはi番目のマシンの平均ゲインです。 
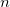すべてのマシン上のゲームの数、および 
i番目のマシンでプレイされたゲームの数。実際には、ボードゲームツリーの動きを検索するためにUCB式の修正がよく使用されます。
たとえば、これ：
、
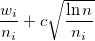
こっち 
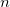これは、i番目のノードの勝利数です。 -i番目のノードへの訪問数、および すべての隣接ノードへの訪問の数。 cは、検索の幅と深さの間の望ましいバランスを設定するために使用される定数です。 大きいほど、検索は深くなります。名前が示すように、UCT（Upper Confidence bounds to Trees）アルゴリズムはUCBアプローチを使用してツリーを検索します。 アルゴリズムの各段階を段階的に考えてみましょう。
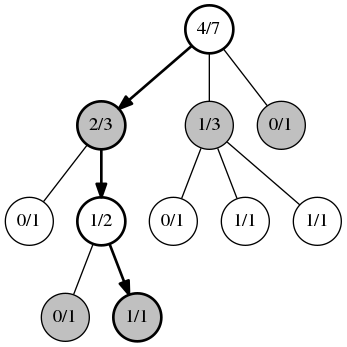
最初のフェーズ、 選択 。 私たちは、各ポジションを多腕バンディットのタスクと考えています。 各ステージのノードは、UCBアルゴリズムに従って選択されます。 このフェーズは、すべての子ノードが勝利統計を持たないノードが見つかるまで有効です。 図では、ノードの最初の値は勝ちの数、このノードの2番目の合計ゲーム数です。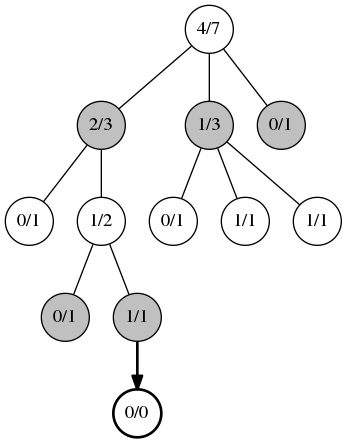
2番目のフェーズである拡張 。 UCBアルゴリズムを適用できなくなると、新しい子ノードが追加されます。
第三段階、 シミュレーション 。 前の段階で作成されたノードから、ゲームはランダムに開始されます。または、ヒューリスティックを使用する場合、完全にランダムな移動ではありません。 ゲームはゲームの最後まで進みます。 ここでは、勝者に関する情報のみが重要であり、ポジションの評価は重要ではありません。
第4フェーズ、 逆伝播 。 この段階で、プレイしたゲームに関する情報がツリー全体に広がり、以前に渡された各ノードの情報が更新されます。 これらの各ノードはゲーム数の指標を増やし、勝者に一致するノードも勝利数を増やします。 アルゴリズムの最後に、最も多くアクセスされたノードが選択されます。
UCTは常に最適な移動のみを選択するわけではなく、成功していないノードを定期的に検査します。 式の2番目のパラメーターは、あまり頻繁にアクセスされないノードに対してゆっくりと成長しています。 そして最終的に、ある段階で、アルゴリズムはそのような動きを優先的な動きとして選択します。 動きが予想を満たしていれば、次回はより高い確率で選択されます。
最適な動きを見つけるための他のアルゴリズムと比較して、UCTには次の利点があります。
- UCTは、作業のどの段階でも安全に停止できます。 そして、停止時には、ルートノードからのすべての動きを均等に計算します
アルファベータアルゴリズムを停止する例。 「？」記号の付いたノードは調査されていないことがわかります。
- 木は非対称に成長し、他の動きよりも優先される動きを探索します。 したがって、列挙のオプションが多数あるゲームの他のアルゴリズムと比較して、効率が大幅に向上します。
なぜなら ランダムに選択された動きはほとんど意味がなく、一般的な方向性がないため、特定のゲームに関する情報に基づいたさまざまなヒューリスティック手法を使用して、アルゴリズムの動作を改善します。 これらの方法の1つは、テンプレートの使用です。
Goで石を切るための3x3テンプレートの例を次に示します。
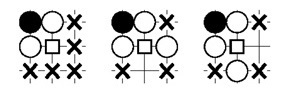最初のパターンが一致する場合、動きは興味深いと見なされますが、2番目と3番目のパターンは一致しません。 つまり、白いグループを「カット」することができます。 ボックスは、関心のある位置を示しています。テンプレートは、ツリー内の移動を選択する段階と、シミュレーションの段階の両方で使用できます。 多くの場合、そのようなパターンは最後に行われた動きの近くのどこかに求められます。 これは、現在の移動が以前の移動に対する応答ではなく、おそらく近くのどこかで行われるためです。
前後の一連の例。 左側は通常のUCTを使用したゲームの状況、右側はテンプレートを使用したUCTです。
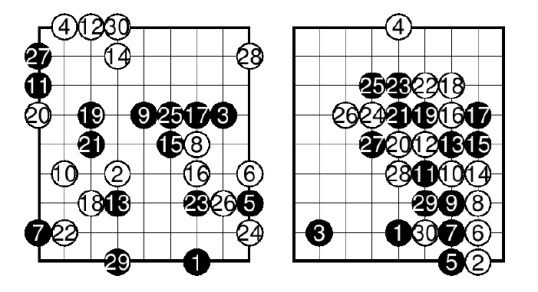最初の図では、石がボード全体にランダムに配置されていることがわかります。ほとんどの場合、テンプレートは手動で作成されますが
、自動生成の
例も
あります。
ボード全体にスプレーされず、余分なオプションの計算を間違えないようにするため。 動きを探索する最も重要な領域を選択できます。 明らかに、現時点ですべての闘争がボードの特定のコーナーの1つのグループに集中している場合、周りの空き領域を考慮することは意味がありません。 そのような領域を定義するためのアルゴリズムはこの記事の範囲を超えていますが、興味がある人はここで詳しく読むことができます：
Common Fate Graph 。
UCTアルゴリズムは、複数のスレッドで同時に実行できます。 計算を並列化する方法は次のとおりです。
- ノードの並列化、同じノードからのゲームの同時シミュレーション。
- ルートの並列化、独立したツリーの構築。
- ツリーの並列化、複数のスレッドによる1つのツリーの共同構築。
これがおそらく、モンテカルロアルゴリズム、特にUCTについて述べたいことのすべてです。 一般に、追加の変更を考慮したアルゴリズムは、良いゲーム結果を示します。 このステートメントは、すべての最新のGoプログラムで使用されているという事実によってサポートされています。 皆さんにとっても役に立つことを願っています。