この記事では、ニューラルネットワークの導入とその実装例について説明します。最初の部分では、ホップフィールドニューラルネットワークを例として使用して、ニューラルネットワークの簡単な理論的紹介を行います。ネットワークのトレーニング方法とそのダイナミクスの説明方法が示されています。 2番目の部分では、C ++言語を使用して最初の部分で説明したアルゴリズムを実装する方法を示します。開発したプログラムは、ノイズから重要な画像を消去するニューラルネットワークの能力を明確に示しています。記事の最後に、プロジェクトのソースコードへのリンクがあります。

理論的説明

はじめに

まず、ニューロンとは何かを判断する必要があります。生物学では、ニューロンは神経系を構成する特殊な細胞です。生体ニューロンは図1に示す構造をしています。

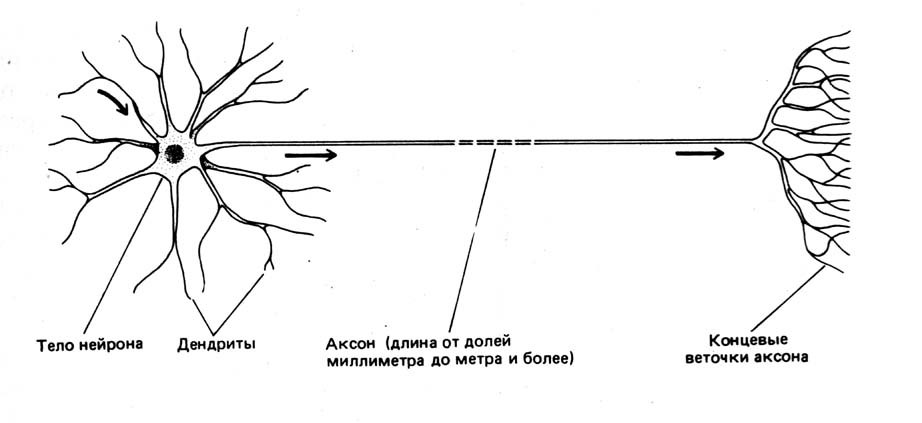
図1ニューロン回路

ニューラルネットワークは、ニューロンとその関係のセットとして導入できます。したがって、人工（非生物学的）ニューラルネットワークを決定するには、次のことが必要です。

ネットワークアーキテクチャを定義します。
個々のネットワーク要素のダイナミクスを決定します-ニューロン;
ニューロンが相互作用するルールを定義します。
学習アルゴリズム、つまり問題を解決するために関係を形成します。

ニューラルネットワークのアーキテクチャは、ホップフィールドネットワークを使用します。このモデルは、明らかに、神経科学で最も一般的な数学的モデルです。これは、そのシンプルさと明快さによるものです。ホップフィールドネットワークは、非常に信頼性の低い要素のネットワークでメモリを構成する方法を示しています。実験データは、失敗したニューロンの数が50％に増加すると、正解の確率が100％に非常に近いことを示しています。ニューラルネットワーク（脳など）とフォンノイマンコンピューターの表面的な比較でさえ、これらのオブジェクトがどれほど異なるかを示しています。たとえば、ニューロンの状態の変化の頻度（「クロック周波数」）は200 Hzを超えない一方で、最新のプロセッサの要素の状態の変化の頻度は数GHz（ $10 ^ 9$ Hz）。
ホップフィールドネットワークの正式な説明

ネットワークはN個の人工ニューロンで構成され、各ニューロンの軸索は残りのニューロンの樹状突起に接続され、フィードバックを形成します。ネットワークアーキテクチャを図に示します。 2。

図2ホップフィールドニューラルネットワークアーキテクチャ

各ニューロンは、次の2つの状態のいずれかになります。

$S（t）\ in \ {-1; +1 \}$

どこで $S（t）$ -現在のニューロンの状態 $t$ 。ニューロンの「励起」は $+1$ 、および「抑制」 $-1$ 。ニューロンの状態の離散性は、その機能の非線形でしきい値の性質を反映しており、神経生理学では「すべてまたは無」の原則として知られています。

経時的な状態のダイナミクス $私は$ のネットワークの番目のニューロン $N$ ニューロンは、離散動的システムによって記述されます。

$S_ {i}（t + 1）= sign [\ sum \ limits_ {j = 1} ^ N J_ {i、j} S_ {i}（t）]、\ quad i、j \ in1、..、N$

どこで $J_ {i、j}$ -樹状突起の相互作用を記述する重みの行列 $私は$ 軸索のあるニューロン $j$ 番目のニューロン。

それは注目に値する $J_ {i、i} = 0、\ quad i = 1、..、N$ そしてケース $\ sum \ limits_ {j = 1} ^ {N} J_ {i、j} S_ {i}（t）= 0$ 考慮されません。

トレーニングとノイズ耐性

ホップフィールドネットワークトレーニングの週末の画像 $\ zeta _ {\ mu} ^ {in}$ 行列の要素の値を計算することに縮小 $J_ {i、j}$ 。正式には、学習プロセスを次のように説明できます。認識するにはニューラルネットワークをトレーニングする必要があります。 $M$ 示されている画像 $\ {\ zeta _ {\ mu} ^ {in}、\ mu = 1、..、M \}$ 。入力画像 $\上線{\ zeta _ {\ mu} ^ {in}}$ を表します： $\上線{\ zeta _ {\ mu} ^ {in}} = \ zeta _ {\ mu} ^ {in} + \ cute {\ zeta}$ どこで $\急性{\ゼータ}$ -元の画像にノイズが重畳されている $\ zeta _ {\ mu} ^ {in}$ 。
実際、ニューラルネットワークのトレーニングは、画像の空間におけるノルムの定義です $|| \ zeta _ {\ mu} ^ {in}-\上線{\ zeta _ {\ mu} ^ {in}} ||$ 。次に、入力画像のノイズを除去することは、この式を最小化することとして説明できます。

ニューラルネットワークの重要な特徴は、キー画像の数の比率です $M$ 覚えておくことができるのは、ネットワークのニューロンの中です $N$ ： $\ alpha = \ frac {M} {N}$ 。ホップフィールドネットワークの場合、値 $\アルファ$ 0.14以下。

キー画像の正方形サイズのマトリックスの計算は、ヘブの規則に従って実行されます。

$J_ {i、j} = {1 \ over N} \ cdot \ sum \ limits _ {\ mu = 1} ^ {M} \ big [\ zeta_ {i、\ mu} ^ {in} \ cdot \ zeta_ {j 、\ mu} ^ {in} \ big]}$

どこで $\ zeta_ {j、\ mu} ^ {in}$ 意味する $j$ 画像要素 $\ zeta _ {\ mu} ^ {in}$ 。

乗算演算の可換性により、等式が
$J_ {i、j} = J_ {j、i}$

認識のために表示される入力画像は、システムの初期データに対応し、動的システムの初期条件として機能します（2）：

$S_ {i} = \上線{\ zeta _ {\ mu} ^ {in}}$

式（1）、（2）、（3）、（4）はホップフィールド人工ニューラルネットワークを決定するのに十分であり、その実装に進むことができます。

ホップフィールドニューラルネットワークの実装

上で定義したホップフィールドニューラルネットワークの実装は、C ++で行われます。実験を簡単にするために、ニューロンのタイプとその伝達関数に直接関連するタイプの基本的な定義をsimple_neuronクラスに追加し、以下の導関数を定義します。

ニューロンに直接関連する最も基本的なタイプは次のとおりです。

重みのタイプ（ フロート選択）;
ニューロンの状態を記述する型（2つの有効な値を持つ列挙型が導入されました）。

これらのタイプに基づいて、残りの基本タイプを入力できます。

当時のネットワークの状態を記述するタイプ $t$ （標準ベクトルコンテナが選択されています）;
ニューロンリンケージウェイトの行列を記述するタイプ（コンテナベクトルコンテナが選択したベクトル ）。

リスト1.新しいタイプの定義

struct simple_neuron { enum state {LOWER_STATE=-1, UPPER_STATE=1}; typedef float coeff_t; <<(1) typedef state state_t; <<(2) ... }; typedef simple_neuron neuron_t; typedef neuron_t::state_t state_t; typedef vector<state_t> neurons_line; <<(3) typedef vector<vector<neuron_t::coeff_t>> link_coeffs; <<(4)

ネットワークの学習、または行列要素の計算 $J_ {i、j} = J_ {j、i}$ （3）に従って、学習イメージのリストを受け取り、タイプlink_coeffs_tのオブジェクトを返すlearn_neuro_net関数によって実行されます。値 $J_ {i、j}$ 下三角要素についてのみ計算されます。上三角要素の値は、（4）に従って計算されます。リスト2に、 learn_neuro_netメソッドの一般的なビューを示します。

リスト2.ニューラルネットワークトレーニング

 link_coeffs learn_neuro_net(const list<neurons_line> &src_images) { link_coeffs result_coeffs; size_t neurons_count = src_images.front().size(); result_coeffs.resize(neurons_count); for (size_t i = 0; i < neurons_count; ++i) { result_coeffs[i].resize(neurons_count, 0); } for (size_t i = 0; i < neurons_count; ++i) { for (size_t j = 0; j < i; ++j) { neuron_t::coeff_t val = 0; val = std::accumulate( begin(src_images), end(src_images), neuron_t::coeff_t(0.0), [i, j] (neuron_t::coeff_t old_val, const neurons_line &image) -> neuron_t::coeff_t{ return old_val + (image[i] * image[j]); }); result_coeffs[i][j] = val; result_coeffs[j][i] = val; } } return result_coeffs; }

ニューロンの状態の更新は、 neuro_net_systemファンクターを使用して実装されます。 _do functorメソッドの引数は初期状態です $S_ {i}（0）$ 、認識可能な画像（（5）に準拠）-タイプneurons_lineのオブジェクトへの参照。

functorメソッドは、neurons_lineタイプの送信されたオブジェクトを、その時点のニューラルネットワークの状態に変更します。 $T$ 。値は厳密に固定されておらず、次の式によって決定されます。

$S_ {i}（T-1）= S_ {i}（T）$

つまり、各ニューロンの状態が1「サイクル」で変化していない場合。

（2）を計算するために、2つのSTLアルゴリズムが適用されました。

std ::ニューロンの重みと状態の積の合計を計算するためのinner_product （つまり、特定の $私は$ ）;
std ::各ニューロンの新しい値を計算するように変換します（つまり、可能なそれぞれについて上記の項目を計算します） $私は$ ）

neurons_net_systemファンクターのソースコードとsimple_neuronクラスのcalculateメソッドをリスト3に示します。

リスト3.ニューラルネットワークの操作を実装するFunctor

 struct simple_neuron { ... template <typename _Iv, typename _Ic> static state_t calculate(_Iv val_b, _Iv val_e, _Ic coeff_b) { auto value = std::inner_product( val_b, val_e, coeff_b, coeff_t(0) ); return value > 0 ? UPPER_STATE : LOWER_STATE; } }; struct neuro_net_system { const link_coeffs &_coeffs; neuro_net_system(const link_coeffs &coeffs): _coeffs(coeffs) {} bool do_step(neurons_line& line) { bool value_changed = false; neurons_line old_values(begin(line), end(line)); link_coeffs::const_iterator it_coeffs = begin(_coeffs); std::transform( begin(line), end(line), begin(line), [&old_values, &it_coeffs, &value_changed] (state_t old_value) -> state_t { auto new_value = neuron_t::calculate( begin(old_values), end(old_values), begin(*it_coeffs++) ); value_changed = (new_value != old_value) || value_changed; return new_value; }); return value_changed; } size_t _do(neurons_line& line) { bool need_continue = true; size_t steps_done = 0; while (need_continue) { need_continue = do_step(line); ++steps_done; } return steps_done; } };

入力画像と出力画像をコンソールに出力するために、 neurons_line_print_descriptorタイプが作成されました 。これには、画像へのリンクとフォーマット形式（画像が入力される長方形の幅と高さ）が格納されます。このタイプでは、演算子<<がオーバーライドされます。 Neurons_line_print_descriptorタイプおよびストリーム出力演算子のソースコードをリスト4に示します。

リスト4.ニューラルネットワークの状態フローへの出力

 struct neurons_line_print_descriptor { const neurons_line &_line; const size_t _width; const size_t _height; neurons_line_print_descriptor ( const neurons_line &line, size_t width, size_t height ): _line(line), _width(width), _height(height) {} }; template <typename Ch, typename Tr> std::basic_ostream<Ch, Tr>& operator << (std::basic_ostream<Ch, Tr>&stm, const neurons_line_print_descriptor &line) { neurons_line::const_iterator it = begin(line._line), it_end = end(line._line); for (size_t i = 0; i < line._height; ++i) { for (size_t j = 0; j < line._width; ++j) { stm << neuron_t::write(*it); ++it; } stm << endl; } return stm; }

ニューラルネットワークの例

実装の健全性をテストするために、ニューラルネットワークは2つの主要なイメージでトレーニングされました。

図3キー画像

歪んだ画像が入力されました。ニューラルネットワークは、ソースイメージを正しく認識しました。歪んだ画像と認識された画像を図4、5に示します

図4画像認識1

図5画像認識2

プログラムは、AppName WIDTH HEIGHT SOURCE_FILE [LEARNE_FILE_N]という形式の行を使用してコマンドラインから起動されます。ここで、

  AppNaame-実行可能ファイルの名前。
 WIDTH、HEIGHT-出力およびキー画像が収まる長方形の幅と高さ。
 SOURCE_FILE-初期イメージを含むソースファイル。
 [LEARNE_FILE_N]-キーイメージ（スペースで区切られた）を持つ1つ以上のファイル。

ソースコードはGitHub-> https://github.com/RainM/hopfield_neuro_netに投稿されています

リポジトリには、Visual Studioプロジェクト（VS2015がプロジェクトを正常にコンパイルする）または通常のUnix Makefileを生成できるCMakeプロジェクトがあります。

中古文学

G.G. マリネツキー。相乗作用の数学的基礎。モスクワ、URSS、2009年。
WikipediaのHopfield_Neural_Networkの記事。

ホップフィールドフィンガーニューラルネットワーク

理論的説明

はじめに

トレーニングとノイズ耐性

ホップフィールドニューラルネットワークの実装

ニューラルネットワークの例

More articles: