Wolfram言語を使用して導出された新しいベッセル誘導体

ベッセルが同じ名前の関数を導入してから約200年後、複素平面全体で有効なパラメーターに関する導関数の式が見つかりました

このブログでは、特別な関数（主にベッセル関数と関連関数）のいくつかの未知の派生物について説明し、超幾何学的およびその他の関数のパラメーターに関する分化の歴史と現在の状態に触れます。 主な新しい式の1つ（以下で詳細）は、最も一般的な特殊関数の1つであるベッセル関数Jの1次導関数の閉じた式です。



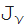
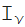
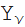
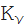
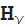
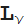
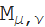
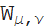
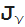
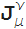
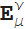
数理物理学の多くの関数（つまり、頻繁に使用されるため特別な名前を持つ関数）は、いくつかの変数に依存します。 それらの1つは通常引数と呼ばれ、他の1つは通常パラメーターまたはインデックス（アイコン）と呼ばれます。 これらの特殊関数には、任意の数のパラメーターを指定できます。 たとえば（ Wolfram関数サイトを参照）、ベッセル関数 （z）および （z）、ノイマン （z）、マクドナルド （z）、およびStruve （z）および （z）1つのパラメーター（いわゆるインデックス）のみがあり、Whittaker関数 （z）および （z）、および縮退した超幾何関数 （a; b; z）とU（a、b、z）には2つのパラメーターがあります。 怒りの機能 （z）および （z）、およびWeber関数 （z）および （z）1つまたは2つのパラメーターを持つことができます（2つのパラメーターの場合、それらはAngerおよびWeberの一般化関数と呼ばれます）。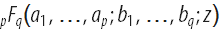 AppelおよびHumbert関数には3〜5個のパラメーターがあり、一般化された超幾何関数などのより複雑な特殊関数 、任意の有限数のパラメーターを持つことができます。

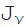
他のプロパティの中でも、特殊関数の微分は、これらの変数が変化するときの微分が関数の動作を特徴付けるので、重要な役割を果たします。また、これらの関数の微分方程式の研究にも重要です 原則として、その引数による特別な関数の区別は、大きな困難を提示しません。 このような導関数の最大のコレクションは、200以上の関数の1次、2次、記号、さらには分数次数を含み、Wolfram Functions Webサイトの「微分」セクションで利用できます（ このセクションには、ベッセル関数の21導関数の式が含まれているとしましょう （z））、またはYuの本A. Brychkov Handbook of Special Functions ）。 これらの式のほとんどは、 Wolfram言語でも直接利用できます。 新しいMathematicalFunctionDataおよびEntityValue関数を使用して取得できます。

ただし、パラメータに関する導関数（引数とは対照的に）は一般に計算がはるかに困難です。 数学物理学の最も頻繁に遭遇する特殊関数の1つ（パラメーターνに関する ）の1次導関数を含む上記の式が閉じた形で発見されたのはごく最近であり、これはおそらく驚くべき事実が一般的な問題の複雑さを示していることは注目に値します。 したがって、典型的な例としてベッセル関数Jを使用して、この特殊関数の差別化の歴史について簡単に説明します。

デリバティブの計算は必ずしも簡単ではありません

多くの場合、人々は、数学的分析に精通していても、統合は難しく、差別化は簡単だと考える傾向があります。 「一般的な」知恵は知られており、「 差別化は技術の問題であり、統合は芸術である」 と述べています。 ただし、このステートメントは、微分が再び基本関数（またはその組み合わせ）につながる基本関数に対してのみ完全に当てはまります。 微分がパラメーターによって実行される場合、通常、より一般的なクラスの複雑な関数になります。

パラメーターによる微分と引数による微分の違いは、ベッセル関数Jで説明できます。 引数zに関するベッセル微分Jはかなり以前から知られており、比較的単純な閉形式を持っています。



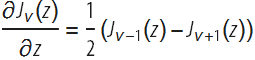
ただし、パラメーターνに関するその導関数の分析計算はより複雑です。 多くの場合、パラメーターに関する導関数は、整数または無限級数の形式で記述できますが、これらのオブジェクトは、他の単純な関数または既知の関数を使用して閉じた形式で表すことはできません。 歴史的に、いくつかの特別な機能は、既知の機能の派生物に簡単な表記法を与えることを唯一の目的として導入されました。 たとえば、 ポリガンマ関数は 、 ガンマ関数の導関数を表す手段として登場しました。

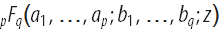
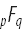
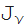
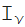
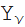
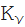
一般化された超幾何関数 そして、その導関数は、理論および応用数学のさまざまな問題を解決する上で重要な役割を果たします（たとえば、量子力学におけるパラメーターに関する導関数の使用に関するLU AncaraniおよびG. Gasaneoの記事を参照 ）。 一般化された超幾何関数は、特別な場合として、最も一般的に使用される多くの基本関数（たとえば、三角関数、双曲線関数、対数関数、逆三角関数）、およびベッセル、シュトルーベ、ケルビン、アンガー-ウェーバーを含む多くの特殊関数を生成します。不完全なガンマ関数と積分関数（指数、サイン、コサイン）。 p = 0 、 q = 1の場合、一般化された超幾何関数 関数のベッセル族が含まれています （z） （z） （z）、および （z）。 たとえば、ベッセル関数Jには、次の超幾何表現があります。







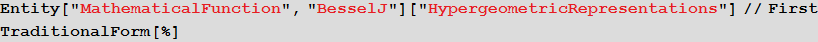
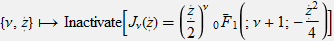
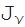
興味深いことに、機能履歴 （z）ほぼ200年前に始まります。 1816-17年のベルリンアカデミー（1819年公開）のレポートでは、 Auflyscheauflösungder Keplerschen Aufgabeの研究で 、フリードリヒヴィルヘルムベッセルは、いわゆるケプラー方程式M = Ee sin（E）を考慮します。ここで、 Mは平均異常、 E異常、およびeはケプラー軌道の離心率です。 この方程式の解は、整数次のベッセル関数を介して（現代の表記法で）表現できます。



この最初の作品では、ベッセルはまだ現代の表記法を使用していませんが、彼の機能はすでに暗黙の形式で表示されます。 たとえば、次の量を使用します（ベッセルはガウスの指定を使用することに注意してください 私のために！ ）：



最近では、この式を次のようにWolfram言語の2つのベッセル関数の合計として書くことができます：





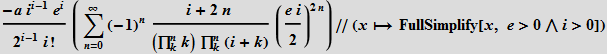
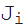
この合計は、正確にベッセル関数-2 ae （ei）：





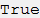
1824年の彼の次の作品では、ベッセルはほとんど現代の表記法（置換J I ）を使用して、彼の機能を示しています。







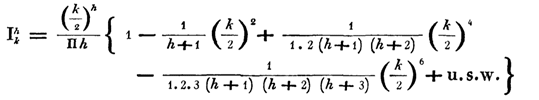
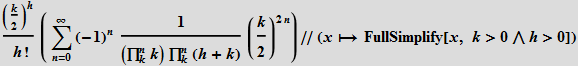
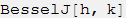
また、次のようなこの機能の基本的な関係も導き出します。







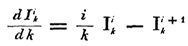
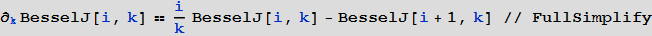
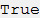
一般的なベッセル関数のさまざまな特殊なケースは、ベルヌーイ、オイラー、ダランベールなどの著書にすでに記載されています（詳細については記事を参照してください）。 今日のベッセル関数に関する主な参考書は、G。N.ワトソンによる古典的なモノグラフであり、「 ベッセル関数の理論 」であり、1922年の初版と比較して繰り返し再版され、実質的に補足されています。

したがって、引数zに関するベッセル関数Jの導関数は19世紀の初めから知られていますが、20世紀半ばまでに、インデックスに関する導関数の特殊なケースが見つかりました。 ν= 0,1,2、...およびν= 1/2におけるνに関するいくつかのベッセル関数の導関数は1935年にJ. R.エアリーによって与えられ、これらの点におけるベッセル族の他の関数の表現はV. Magnusの本で与えられました。 、F。BeitmanおよびR. P. Soni「 数理物理学の特殊関数の公式と定理 」（1966）：



任意の半整数ν値の一般化は、次のように、 国際抽象および応用分析会議 （Hanoi、2002）で発表されました。



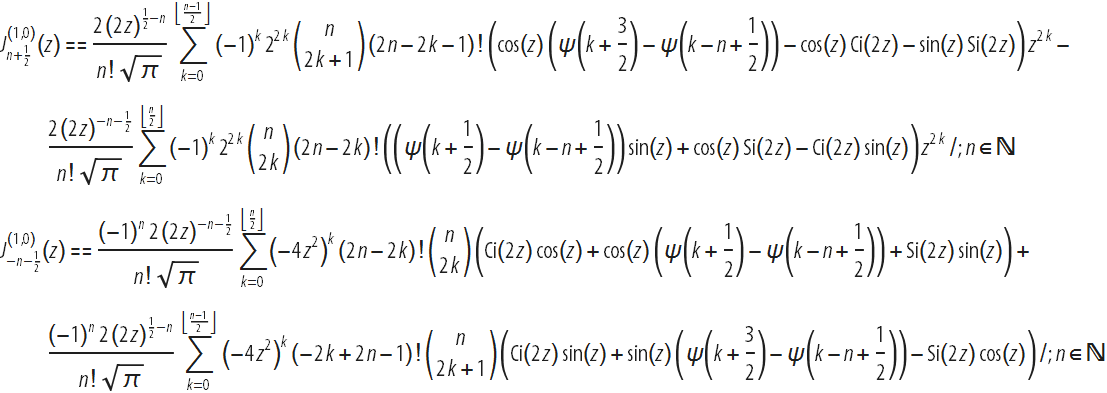
これらの結果は、整数および半整数点でのStruve関数のパラメーターに関する導関数の式とともに、2004年から2005年に公開されました。 アンガー関数とウェーバー関数、ケルビン関数、不完全ガンマ関数、放物線シリンダー関数、ルジャンドル関数とガウス関数、一般化および縮退超幾何関数のパラメーターに関して微分するためのさまざまな新しい公式は、特殊関数のハンドブックにあります：微分、積分、シリーズなどフォーミュラ 。」 簡単な概要と参考資料については、 H。Cohlを参照してください。

これらのすべての結果で、パラメータの任意の値に対する閉じた形のベッセル関数の最初の導関数が2015年にのみ得られたことはおそらく驚くべきことでしょう（Y. A. Brychkov、「 インデックスに関するベッセル関数の高次導関数 」、2016年） 。 それらは、ベッセル関数と一般化された超幾何関数の積の組み合わせとして表されます。 例：



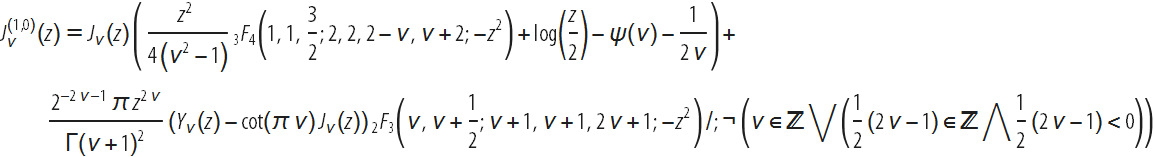
以下のグラフは、ベッセル関数の動作に関する洞察を提供します。 （z）関心のある分野におけるその派生物。 最初に、（実際のν - z平面で）の一次導関数の式を与えます （z） νに関して（記事の冒頭の式を参照）：





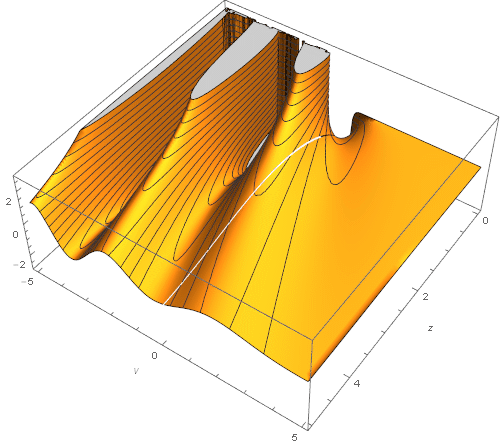
固定インデックス、つまりν = πの場合、ベッセル関数のグラフと最初の2つの導関数（引数とインデックスに関する）を示します。





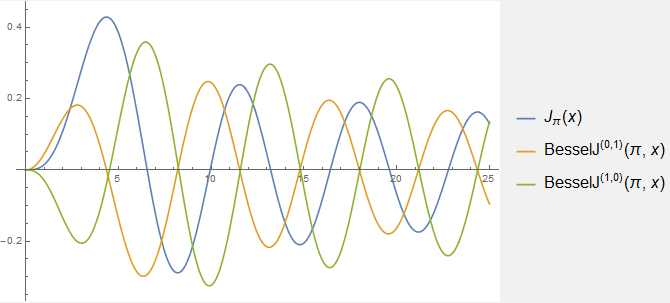
（ zに関して、およびνに関して）導関数がほぼ一致するゼロを持っていることに注意することは興味深いです。

どうやってこれを手に入れたの？

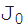
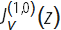
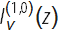
古典的な関数（ベッセル関数の導入からほぼ300年後であっても注目に値する （z）は1732年にダニエルベルヌーイによって導入されました）、以前のように、そのような関数に関連する新しい比較的単純な式が見つかります。 実際、上で紹介した導関数の式 （デリバティブの対応する結果とともに 、ノイマン、マクドナルド、ケルビンの機能）はWolfram言語を使用して取得されました。 これらのデリバティブがどのように検索されたかに関する詳細な情報は、 ここに公開されています 。 この投稿では、他の特別な機能に使用できるアプローチのオプションの1つのスケッチのみを示します。

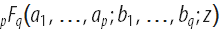
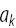
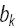
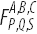
まず、ベッセル関数と、現在関心のある他の関数が超幾何型の関数であることを思い出してください。 しかし、1つの変数の一般的な超幾何関数のパラメーターによる微分 複数の変数の超幾何型のより複雑な関数が必要です（LU AncaraniとG. Gasaneoの記事を参照）。 「上位」パラメーターに関する1次導関数 、および「下位」パラメータに関するシンボリック整数次数mのすべての導関数 一般化された超幾何関数は、Campge de Ferrier超幾何関数に関して表現できます。 次の式による2つの変数：





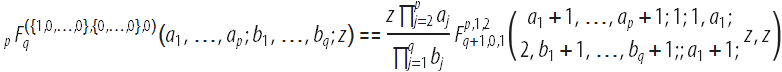
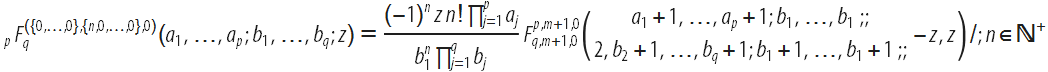
上記のCampéde Ferrierの超幾何関数は、2行で定義されます （ こちらとこちらをご覧ください）。



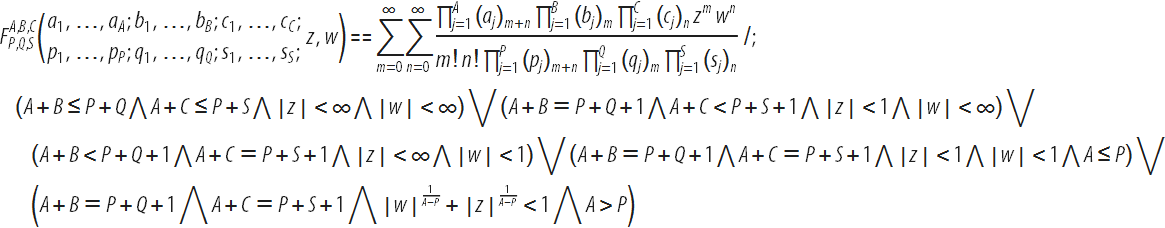
Campe de Ferrier関数は、2つの変数への超幾何関数の一般化と考えることができます。



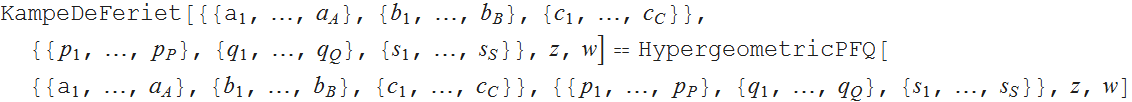
関数の対応する正規化されたバージョンは、Pohhammerキャラクターの積を置き換えることによって決定することもできます。 上の分母で 。

Campe de Ferrier関数は、パラメータに関するベッセル関数Jの導関数を表すために使用できます。



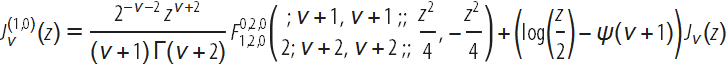
この式は、1つの変数の超幾何関数を含む上記の単純な式と一致しますが、これはすぐにはわかりません（多次元超幾何関数を1次元超幾何関数のみを含む式に単純化するための式の完全なセットはまだありません）。

3つのMeyer G関数の積からMellin変換を計算すると、 2変数の一般化された超幾何関数の上記の定義と同様の二重級数も発生します 。



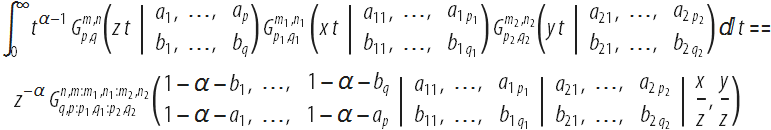
この式の右辺には、2つの変数のMeyer G関数が含まれます。一般的な（非対数）場合、G-の2つの式（ first 、 second ）との類推により、いくつかの係数を持つCampe de Ferrier超幾何関数の有限和として表すことができます1つの変数のMeyer関数。 最後に、超幾何関数の実数部と虚数部が実パラメーターを使用して1つの変数z = x + iyから分離されると、カンペドフェリエ関数も発生します。


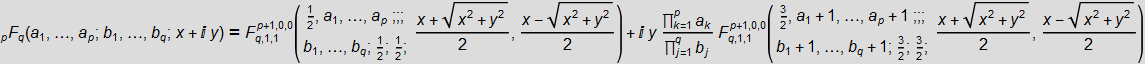
（上記の式はE. D. Krupnikovによって導出されましたが、公開されていません）。

近年、多くの変数の超幾何関数が、場の量子論、化学、機械工学、通信理論、レーダーなどの分野での用途を増やしていることに注目すべきです。 多くの実用的な結果は、そのような関数を使用して表すことができるため、この分野の主な結果のほとんどは、応用科学文献で得られます。 理論数学におけるそのような関数の理論は、まだ比較的不十分に開発されています。

Wolfram言語の文字派生物

シンボリックデリバティブを含むこれらの新しい興味深い数式の作成者であるYuri Brychkovは、私たちのチームのメンバーであり、この絶えず発展している数学の分野をユーザーの注意を引くことができます。 また、 Mathematicaシステムの新しい機能（Wolfram Language）-Entityを自由に使用できることも幸運です。これにより、特に、数週間または数日以内に、計算可能な形式で、言語が使用されるすべてのプラットフォームで新しい結果を迅速に表示できますWolfram言語、ユーザーへ。 たとえば、Mathematicaでは、次の式を計算できます。





したがって、この記事の主要な公式が得られます。 最初にシンボリック値νおよびzを代入し、式を取得することにより、数式を数値的に確認できます。





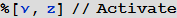
次に、左部分と右部分を分離し、引数とパラメーターをランダムな値に置き換えます。





左辺の数値導関数は、制限手順を使用してWolfram言語で計算されます。 左辺と右辺の平等性、したがって、導関数の元の式の正確性は明らかです。

この記事で言及され、 EntityValueを介してのみ利用可能なシンボリックおよびパラメトリック派生物に関する多くの新しい結果に加えて（Wolfram言語の将来のバージョンでこの機能をより深く統合するには絶え間ない努力が必要です）、この分野の多くの結果がシステムのカーネルに既に実装されていますMathematicaとWolfram言語のコア。 このようなパラメーターの導関数は複雑であるため自動的に計算されませんが、 FunctionExpandコマンドを使用して表示できます。 例：









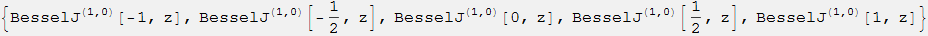
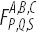
2次以上のベッセル関数と関連関数のインデックスに関する微分は、2変数のCampge de Ferrier超幾何関数の観点から表現できます。 、しかし、結果の式は非常に複雑になる可能性があり、ベルY多項式を含む場合があります。



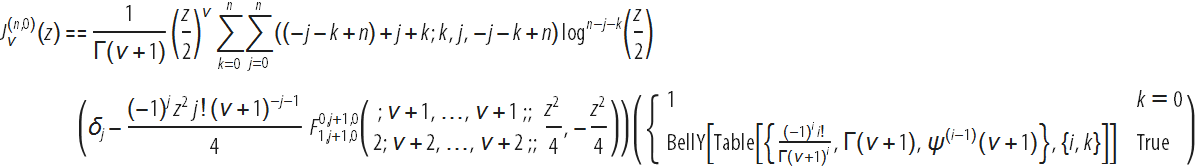
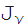
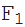
最後の式は、ベッセル関数の表現から生じます （z）関数の構成を通して （;ν+ 1; w）および ：



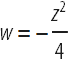
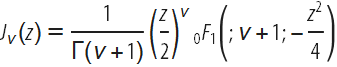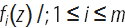
Faa di Bruno式を使用します。これにより、 m関数の合成のn次導関数の式を取得できます。 。 m = 2の場合（ こことここを参照）、たとえば次の式を取得します。



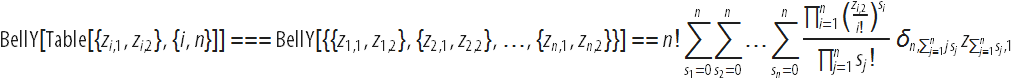
共通のmおよびnに対応する式は、Wolfram言語で取得および検証できます。





一般的な閉形式がないベル多項式Yは、高階微分を表すために通常必要ですが、この投稿の著者の1人であるYuri Brychkovは、ベッセル関数のパラメーターに関してn番目の微分から多項式Yを除去する方法を発見しました。素晴らしい結果を残してくれました。



パラメーターに関する特別な関数の派生物（上記を含む）のすべての既知の式を1か所で確認したいユーザーの便宜のために、これらの式を次の方法で収集して表示しました。

1.表形式（ こちらからダウンロード）。

2. Mathematicaラップトップの形式（ こちらからダウンロード）。

3. 2009年以前に知られていた式のサブセットは、Wolfram Function Siteのさまざまな関数の「Differentiation」セクションで見ることができます（たとえば、このページを参照 ）。

次の投稿では、シンボリックおよびフラクショナルオーダーの導関数の一般的なルールを持つ400以上の関数のコレクションの導関数の閉じた形の表現を与えます。 Wolfram言語で特殊関数の派生物の世界を楽しんで楽しんでください！

Wolframテクノロジーに関する質問については、 info-russia @ wolfram.com までお問い合わせください