こんにちは親愛なる読者。 記事を読んだ後、おそらく論理的な質問があります。「なぜ、実際にこれが必要なのですか?」 このため、最初に、二次方程式を解くために必要な方法は、実際の乾燥した側面よりも数学の道徳的および美的側面でより多く提示されることを事前に通知する必要があると考えます。 また、私のアマチュアのことわざが受け入れられないと思っている読者に、事前に謝罪します。 それでは、
顕微鏡で釘を打ち始めましょう。
一般的な形式の2次の代数方程式(2次でもある)があります。
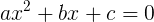
二次方程式から二次関数に渡します。
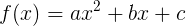
明らかに、そのような引数値を見つける必要がある場合
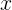
ゼロを返す関数。
Vietaの定理を使用して
、または
判別式を使用し
て 、2次方程式を解くだけでよいようです。 しかし、私たちはこのためにここに集まりませんでした。 デリバティブをもっと良くしましょう!

一階微分の物理的意味の定義に基づいて、引数を置き換えることは明らかです
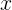
上記で取得した関数では、(特に)この引数で指定されたポイントでの関数
の変化
率を取得します。
次に何をする? 明確ではありません。 理解できない場合には、派生物を再度取得する必要があります。

今回は、特定のポイントでの関数変更(つまり、
加速度 )の "速度の速度"を取得しました。 得られたものを少し分析した後、「加速度」は関数の引数に依存しない定数であると結論付けることができます-これを覚えておいてください。
ここで、少しの物理学と
一様に加速されたモーション (RUD)を思い出しましょう。 武器庫には何がありますか? 確かに、軸に沿った動きの座標を決定するための式があります

希望の動きで:
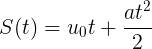
どこで

-時間
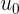
-初期速度
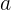
-加速。
元の機能が単なる鉱石であることは容易にわかります。
OREの変位式は、二次方程式を解いた結果ではありませんか?いや 上記のOREの式は、実際にはPONDの速度式を積分した結果です。 またはチャートから
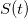
図の領域を見つけることができます。 空中ブランコが出てきます。
鉱石での変位の式は、二次方程式の解から導出されません。 これは非常に重要です。そうしないと、記事に意味がありません。
今、何が何であり、何が欠けているのかを理解することが残っています。
「加速」
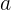
私たちはすでに持っています-それは二次微分です
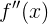
上記の推論。 しかし、初期速度を取得するには
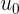
、基本的にはいずれかを取る必要があります
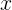
(私たちはそれを
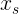
)そして、今それを一次の導関数に代入します

-彼女が求められます。
この場合、疑問が生じます。
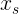
取る必要がありますか? 明らかに、そのような初期速度
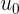
ゼロに等しいため、式「鉱石での移動」は次のようになり始めました。

この場合、検索の方程式を作成します
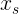
:
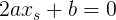
[フレーム付き
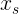
一階微分

]
についてのそのような方程式の根
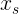
なります:

元の関数の値

そのような引数を使用すると次のようになります。

最初に設定した目標を思い出してください:「引数のそのような値を見つけることが必要です
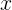
ゼロを返す関数。」 言い換えれば、私たちは

「ゼロにする」必要があります。
これで初期速度、加速度、およびどの方向に進むかがわかったので、次のことに注意してください。
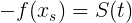
と同様に

次に、すべての既知の量を代入して、次を取得します。
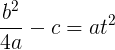
すべてを分割する
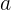
:

次のことが明らかになります。

すべての「パズルの詳細」を一緒に接続します。
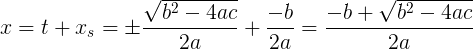
それで、タスクの最終的な解決策を得ました。 一般に、アメリカを発見したわけではありません-判別式を介してラウンドアバウトで二次方程式を解くための公式にたどり着きました。 これには実用的な意味はありません(ほぼ同じ方法で、任意の形式(必ずしも一般的ではない)の1次/ 2次の方程式を解くことができます)。
この記事の目的は、特に、マットの分析への関心を高めることです。 関数と一般的に数学に。
ピーターはあなたと一緒でした、あなたの注意をありがとう!