🔹 🏻 💇🏾 有益な特徴の選択に関する方法論的注記（特徴選択） 🥊 🚶🏼 💃🏽

みなさんこんにちは！

私の名前はアレクセイ・バーナコフです。私はAlign Technologyのデータサイエンティストです。この記事では、データ分析の実験中に実践する機能選択のアプローチについて説明します。

当社では、統計学者と機械学習エンジニアが、患者の治療に関連する大量の臨床情報を分析しています。一言で言えば、この記事の意味は、私たちが利用できるノイズの多い冗長なギガバイトのデータのごく一部に含まれる貴重な知識を抽出することに絞ることができます。

この記事は、データセットの依存関係を見つけることに関心のある統計学者、機械学習エンジニア、および専門家を対象としています。また、この記事に記載されている資料は、データマイニングに無関心でない幅広い読者にとって興味深いものです。この資料では、フィーチャエンジニアリングの問題、特に主要コンポーネントの分析などの方法の適用については取り上げません。

出所

多数の入力変数を持つセットには冗長な情報が含まれ、モデルに正則化機能が組み込まれていない場合、機械学習モデルの再トレーニングにつながる可能性があることが確立されています。有益な特徴（以降IPR ）を選択する段階は、実験中のデータの前処理で必要なステップであることがよくあります。

この記事の最初の部分では、特性を選択する方法のいくつかを確認し、このプロセスの理論的なポイントを検討します。このセクションは、むしろ私たちの見解の体系化です。
記事の第2部では、人工データセットを例として使用して、有益な機能の選択を試み、結果を比較します。
第3部では、議論中の問題に適用される情報理論からの測定値を使用する理論と実践について説明します。このセクションで紹介する方法は斬新ですが、さまざまなデータセットに対して多数のチェックが必要です。

記事で行われた実験は、特定の方法の最適性に対する分析的正当化が与えられないという事実のために科学的であるふりをせず、読者はより詳細で数学的に正確なプレゼンテーションのために情報源を参照します。さらに、免責事項は、特定のメソッドの値が他のデータで変わるため、タスク全体が知的に魅力的であるという事実に基づいています。

記事の最後に、実験結果がまとめられ、Gitの完全なRコードへのリンクが作成されます。

出版前にこの資料を読んでくれたすべての人々、特にVlad ShcherbininとAlexey Seleznevに感謝します。

1）有益な機能を選択する方法と方法。

Wikiに連絡して、IPRメソッドを分類する一般的なアプローチを見てみましょう。

有益な機能を選択するためのアルゴリズムは、ラッパー（ラッピング）、フィルター（フィルタリング）、および組み込み（組み込みマシン）のグループで表すことができます。（ロシア語圏のコミュニティに対する音の曖昧さを考慮して、これらの用語を正確な翻訳なしで残します-私のコメント。）

ラッピングアルゴリズムは、可能な入力変数の空間での検索を使用してサブセットを作成し、利用可能なデータで完全なモデルをトレーニングすることにより、入力の結果のサブセットを評価します。ラッピングアルゴリズムは非常に高価であり、モデルを再トレーニングするリスクがあります。（検証サンプリングが使用されていない場合-私のコメント。）

フィルタリングアルゴリズムは、入力データのサブセットも検索するという点でラッピングアルゴリズムと似ていますが、完全なモデルを起動する代わりに、より単純な（フィルタリング）アルゴリズムを使用して出力変数のサブセットの重要性を推定します。

マシンに組み込まれたアルゴリズムは、トレーニングで事前定義されたヒューリスティックの助けを借りて、入力機能の重要性を評価します。

出所

例。

IPRラッピングアルゴリズムは、選択されたデータで入力変数のサブセットを検索し、その後のトレーニング（ランダムフォレストなど）を実行したり、交差検証でそのエラーを評価したりするなど、メソッドの組み合わせと呼ぶことができます。つまり、反復ごとにマシン全体をトレーニングします（すでに実際に使用できる状態になっています）。

IPRのフィルタリングアルゴリズムは入力変数の列挙と呼ばれ、選択された変数と出力の間の関係の統計的検定によって補完されます。入力と出力がカテゴリカルである場合、入力（または入力の組み合わせセット）と出力との間の独立性についてカイ二乗検定を実行して、p値、および結果として、選択された属性セットの重要性または重要性に関するバイナリ結論を行うことができます。フィルタリングアルゴリズムの他の例は次のとおりです。

入力と出力の線形相関。
カテゴリー入力と連続出力の場合の平均の差の統計的検定;
F検定（分散分析）。

組み込みのIPRアルゴリズムは、たとえば、線形回帰係数に対応するp値です。この場合、p値により、係数とゼロの有意差についてバイナリの結論を出すこともできます。モデルのすべての入力をスケーリングすると、重みのモジュールは重要性の指標として解釈できます。 R ^ 2モデルを使用することもできます。これは、シミュレートされた値でプロセスの分散を説明する尺度です。別の例は、ランダムフォレストに組み込まれた入力変数の重要性を評価する関数です。さらに、人工ニューラルネットワークの入力に対応する重みのモジュールを使用できます。このリストはこれで終わりではありません。

この段階では、この区別が実際にIPRのフィットネス関数の違い、つまり、解決されている問題に関する入力フィーチャの見つかったサブセットの関連性の尺度を示すことを理解することが重要です。その後、フィットネス関数を選択する問題に戻ります。

IPRメソッドのメイングループに少し焦点を合わせたので、入力変数のサブセットを正確に列挙するためにどのメソッドが使用されるかに注意を払うことを提案します。 wikiページに戻りましょう。

スクリーニングのアプローチは次のとおりです。
完全検索
最初の最高の候補者
シミュレーテッドアニーリング
遺伝的アルゴリズム
包含の貪欲な検索
貪欲な例外検索
粒子群最適化
ターゲットを絞った投影追跡
散布検索
可変近傍検索

出所

ロシア語の解釈に精通していないため、一部のアルゴリズムの名前を意図的に翻訳しませんでした。

出力で次の形式の入力インデックスを表す整数のベクトルを取得するため、予測子のサブセットを見つけることは離散タスクです。

入力：1 2 3 4 5 6 ... 1000
選択：0 0 1 1 1 0 ... 1

後でこの機能に戻り、実際にどこにつながるかを説明します。

実験全体の結果は、入力フィーチャのサブセットの検索の構成方法に大きく依存します。これらのアプローチの主な違いを直感的に理解するために、読者にそれらを貪欲と非貪欲の2つのグループに分けることをお勧めします。

貪欲な検索アルゴリズム。

これらは高速であり、多くのタスクで良い結果をもたらすため、頻繁に使用されます。アルゴリズムの欲求は、最終サブセットに入る候補の1つが選択（または除外）された場合、その中に残る（貪欲な包含の場合）か、永久に存在しない（貪欲な例外の場合）という事実にあります。したがって、候補Aが初期の反復で選択された場合、後の反復でサブセットは常に彼と他の候補を含み、Aとともに出力変数のサブセットの重要性のメトリックの改善を示します。反対の状況は除外です：候補Aが除外された後、重要度測定基準への影響が最も少ないか改善されたために削除された場合、研究者は重要度測定基準に関する情報を受信しません。サブセットにはAと他の候補が後で除外されます。

多次元空間で最大値（最小値）の検索と並行して描画すると、貪欲アルゴリズムは局所的な最小値（ある場合）でスタックするか、単一の最小値がある場合（グローバル）に最適なソリューションをすばやく見つけます。

一方、すべての貪欲なオプションの列挙は比較的高速であり、入力間の相互作用を考慮することができます。

貪欲なアルゴリズムの例には、前方選択、前方へのステップ、後方への除去、後方へのステップが含まれます。リストはこれに限定されません。

不要な検索アルゴリズム。

非貪欲アルゴリズムの動作原理は、局所的最小値を回避するために、完全にまたは部分的に形成された機能のサブセット、サブセット間の組み合わせを破棄し、サブセットにランダムな変更を加える機能を意味します。

多次元空間でのフィットネス関数の最大値（最小値）の検索との類似性を引き出すと、非欲張りアルゴリズムはより多くの隣接ポイントを考慮し、ランダムな領域に大きなジャンプを行うことさえできます。

これらのタイプのアルゴリズムの作業をグラフィカルに表示できます。

最初の貪欲な包含：

貪欲でない-確率的-検索：

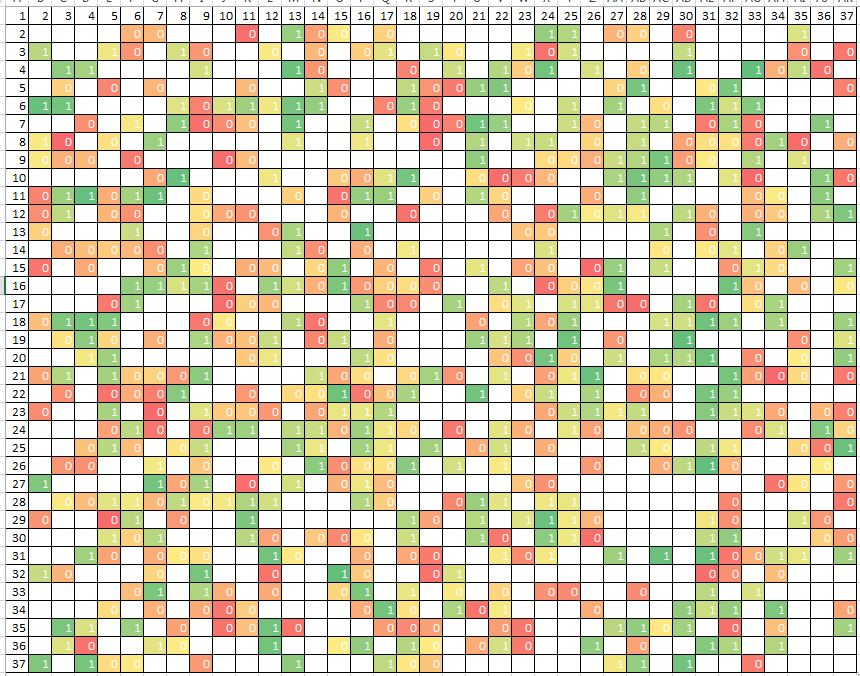
どちらの場合も、インデックスがグラフの軸に沿ってプロットされる2つの入力の最適な組み合わせを1つ選択する必要があります。貪欲なアルゴリズムは、最適な入力を1つ選択し、インデックスを水平に並べ替えることから始まります。そして、選択された入力に2番目の入力を追加して、それらの合計関連性が最大になるようにします。しかし、考えられるすべての組み合わせのうち、部品の1/37のみを完全に通過することがわかります。別の次元を追加すると、渡されるセルの数はさらに小さくなります：約1/37 ^ 2。

同時に、貪欲なアルゴリズムが見つけた最適な組み合わせではない場合、実用的な状況が可能です。これは、2つの入力のそれぞれが個別にタスクに最適な関連性を示さない場合（および最初のステップで選択されていない場合）に発生する可能性があります。

失敗したアルゴリズムはもっと長く見えます：

（O）= 2 ^ n

さらに可能な入力の組み合わせを確認します。しかし、彼は、問題に対するすべての変更を一気に検索することで、おそらく、さらに優れた入力のサブセットを見つける機会があります。

貪欲/非欲張りの確立された二分法を超える検索アルゴリズムがあります。

このような個別の検索の例としては、入力を個別に個別にソートし、出力変数に対する個々の重要性を評価することです。ちなみに、最初の波は、変数の貪欲な包含のためのアルゴリズムで始まります。しかし、非常に高速であることを除いて、このソートで何が良いのでしょうか？各入力変数は「真空中」に存在し始めます。つまり、選択した入力と出力の間の接続に対する他の入力の影響を考慮しません。同時に、アルゴリズムの完了後、出力に対する個々の重要性を示す入力の結果リストは、各予測子の個々の重要性に関する情報のみを提供します。このリストに従って、特定の数の最も重要な予測子を組み合わせると、いくつかの問題が発生する可能性があります。

冗長性（予測子同士の相関の場合）;
選択段階での予測子の相互作用の無視による不十分な情報。
予測変数を取得する必要がある境界線のぼかし。

ご覧のとおり、問題はささいなものではありません。

IPR問題の主な問題は、サブセット検索法とフィットネス関数の最適な組み合わせとして定式化されます。

この声明をさらに詳しく考えてみましょう。 IPR問題は、2つの仮説で説明できます。

a）エラーの表面は単純または複雑です。
b）データに単純な依存関係または複雑な依存関係がある。

これらの質問に対する答えに応じて、検索方法と選択した機能の関連性を判断する方法の特定の組み合わせを選択する必要があります。

表面エラー。

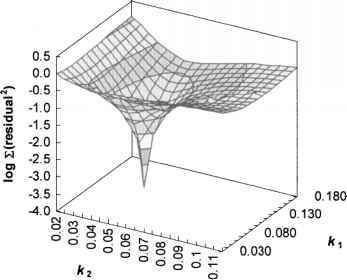
単純な表面の例：

出所

ここでは、2つの入力の組み合わせを選択し、出力との関連性を判断して、勾配の方向に滑らかな表面を下って行き、ほぼ確実に最適なポイントに到達します。

複雑な表面の例：

出所

この場合、同じ問題を解くと、多くの局所的最小値に遭遇し、そこから貪欲なアルゴリズムが抜け出せなくなります。同時に、確率的検索を使用するアルゴリズムでは、より正確な解を見つける可能性が高くなります。

先ほど、予測子のサブセットを見つけることは個別のタスクであると述べました。入力への出力の依存性に相互作用が含まれる場合、空間内のある点から次の点への遷移中に、フィットネス関数の値の急激なジャンプを観察できます。私たちの場合のエラー表面は、多くの場合、滑らかではなく、微分不可能です。

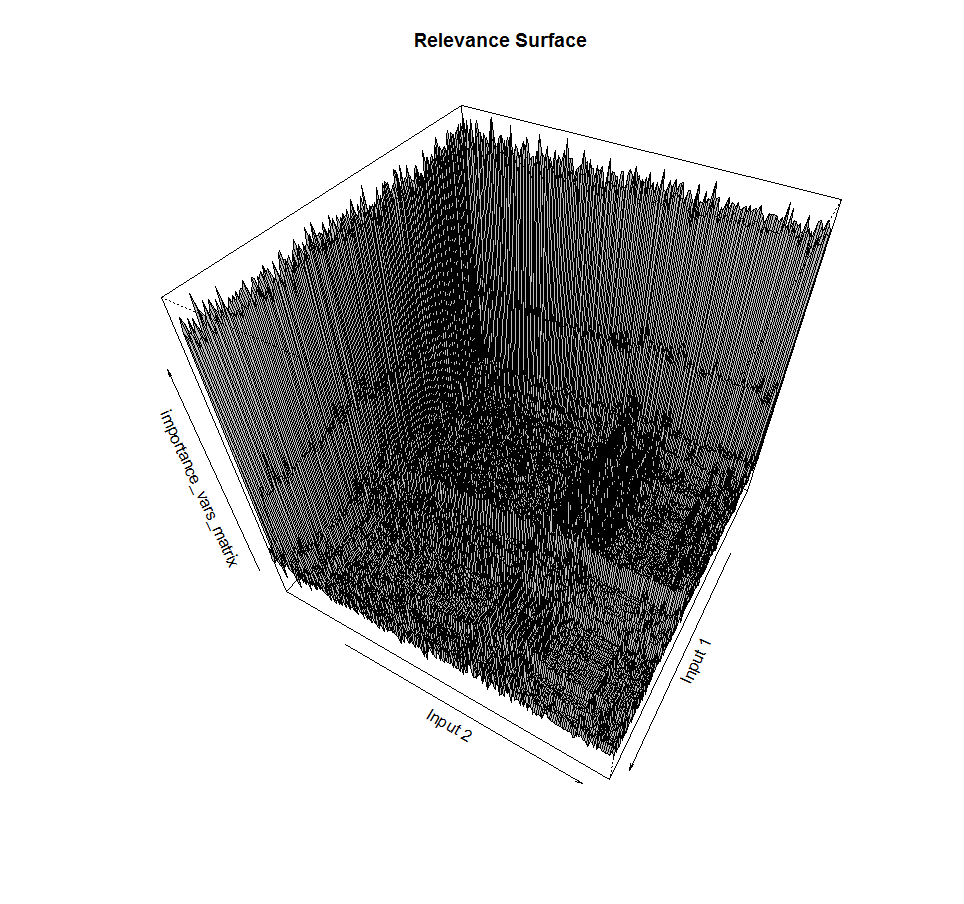
これは、2つの入力のサブセットと、出力変数のサブセットの関連性関数の対応する値を見つける例です。表面は滑らかではなく、ピークがあり、ほぼ同じ値の凹凸のあるプラトーも含まれていることがわかります。欲張り勾配降下法の悪夢。

依存関係。

問題の測定数の増加に伴い、出力変数の依存性が非常に複雑な構造を持ち、多くの入力を伴うという理論上の可能性が増加します。さらに、依存関係は線形と非線形の両方になります。依存関係が予測子と非線形形式の相互作用を意味する場合、たとえば、ランダムフォレストトレーニングまたはニューラルネットワークを使用して、これらの両方のポイントのみを考慮してそれを見つけることができます。依存関係が単純で線形である場合、すべての予測変数のごく一部しか含まれていないため、それを見つけるためのアプローチは、結果としてIPRに至るまで、モデルの品質を評価して、線形回帰モデルに1つまたは複数の入力を含めることに減らすことができます。

単純な依存関係の例：

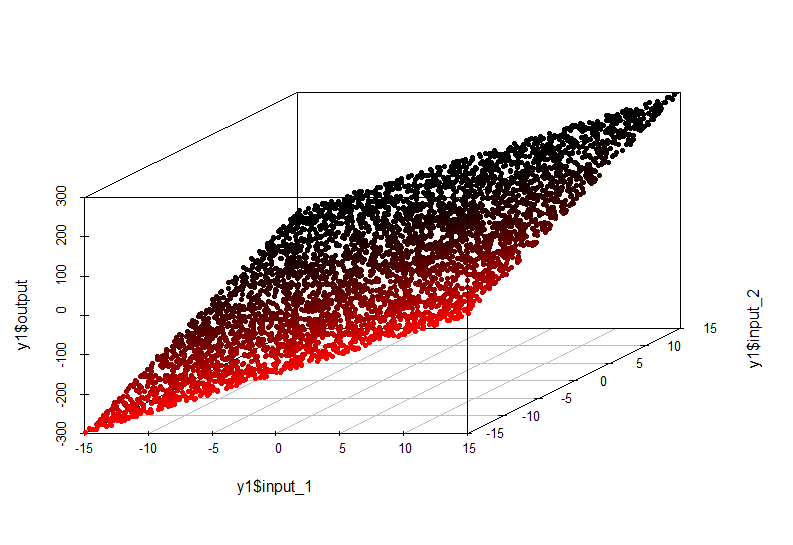
この場合、出力軸に沿った値のinput1およびinput2の値への依存性は、空間内の平面によって記述されます。

出力=入力1 * 10 +入力2 * 10

この依存関係のモデルは非常に単純であり、線形回帰で近似できます。

複雑な依存関係の例：

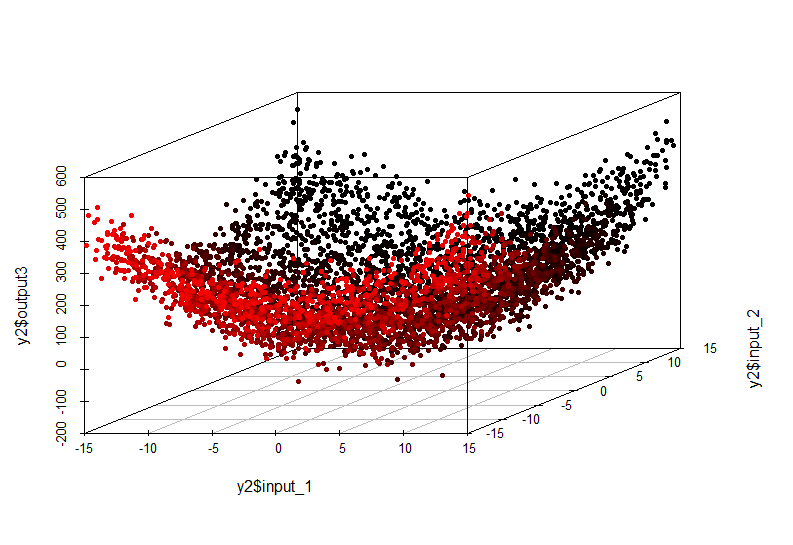
この非線形依存性は、線形モデルを構築しても検出できなくなりました。彼女の外観は次のとおりです。

出力=入力1 ^ 2 +入力2 ^ 2

問題の次元を考慮することも必要です。

入力変数の数が多い場合、可能性のあるすべてのサブセットの総数は次の式で与えられるため、確率的方法（欲張りでない）による最適なサブセットの検索は非常に高価になる可能性があります

m = 2 ^ n、
ここで、nはすべての入力フィーチャの数です。

したがって、そのような多様性の最小値の検索は非常に長くなる可能性があります。一方、貪欲な検索を使用すると、たとえそれが局所的な最小値であり、研究者がそれについて知っているとしても、妥当な時間で最初の近似を行うことが可能になります。

調査中の現象に関する客観的な知識がない場合、入力変数と出力の依存関係がどれほど複雑になるか、入力の最適なサブセットを選択する問題の近似または正確な解を見つけるために最適な入力の数を事前に言うことは不可能です。また、IPRのエラーサーフェスが滑らかで単純であるか、複雑で頑丈であるかを予測することも困難です。

また、私たちは常にリソースに限りがあり、最適な決定を下さなければなりません。 IPRへのアプローチを開発する際の小さな助けとして、次の表を使用できます。

したがって、入力のサブセットとフィットネス関連関数の検索方法のいくつかの組み合わせを考慮する機会が常にあります。最も高価で、おそらく最も効果的な組み合わせは、貪欲な検索とラッパーフィットネス関数です。反復ごとにトレーニングされたモデル（および検証の精度）があるため、選択した入力の関連性の最も正確な測定値を提供しながら、ローカルミニマムを回避できます。

最も安価ですが、常に最も効果的ではないアプローチは、貪欲な検索とフィルター関数の組み合わせです。これは、統計的検定、相関係数、または相互情報量です。

さらに、組み込みメソッドを使用すると、シミュレーションの精度を大幅に損なうことなく、モデルのトレーニング直後にアルゴリズムの観点から不要な多数の入力を除外できます。

問題をさまざまな方法で解決し、最適なものを選択するために何度か試してみるのが良い方法です。

一般的に言えば、有益な特徴の選択は、多次元空間での検索方法の最適な組み合わせと、出力変数に関する選択されたサブセットの関連性に対する最適なフィットネス関数の選択です。

出所

2）合成データに関する有益な特徴の選択に関する実験。

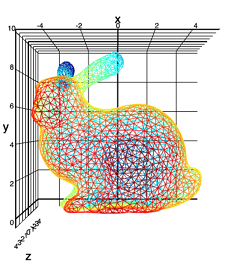
実験データセット（Stanford Bunny）：

ウサギが大好きです。

ポイントの高さ（Z軸）の緯度と経度への依存性を調べます。同時に、2つの情報入力（XとY）の混合にほぼ対応する分布を持つ10個のノイズ変数をセットに追加しますが、変数Zとは関係ありません。

変数X、Y、Zおよびノイズ変数の1つの分布密度のヒストグラムを見てみましょう。

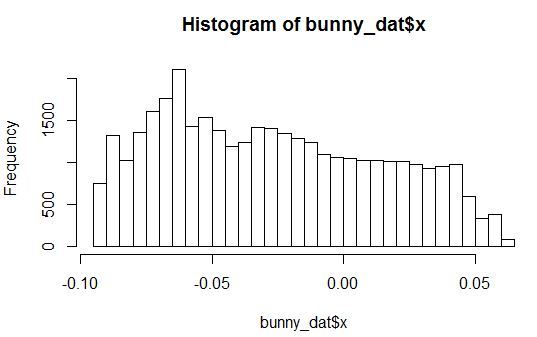
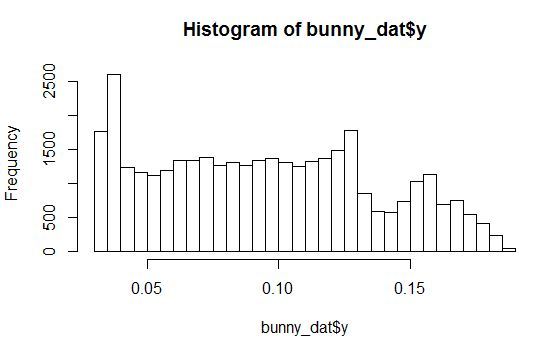
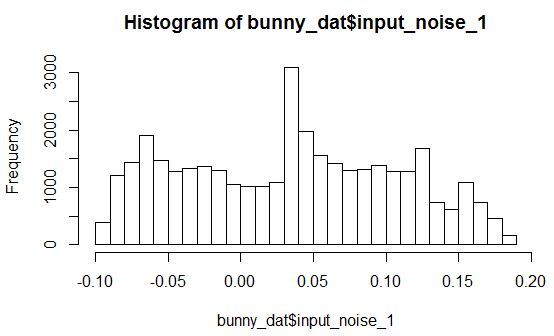
任意のパラメータを持つ分布が見られます。さらに、すべてのノイズ変数は、特定の範囲の値に小さなピークがあるように分布しています。

さらに、データセットは、トレーニングと検証の2つの部分にランダムに分割されます。

データ準備。

コード

library(onion) data(bunny) #XYZ point plot open3d() points3d(bunny, col=8, size=0.1) bunny_dat <- as.data.frame(bunny) inputs <- append(as.numeric(bunny_dat$x), as.numeric(bunny_dat$y)) for (i in 1:10){ naming <- paste('input_noise_', i, sep = '') bunny_dat[, eval(naming)] <- inputs[sample(length(inputs), nrow(bunny_dat), replace = T)] }

実験＃1：重要度を評価する線形関数を使用した入力のサブセットの貪欲検索（フィットネス関数として、検証サンプルでトレーニング済みモデルの決定係数を推定するラッパーオプションを使用します）

コード

 ### greedy search with filter function library(FSelector) sampleA <- bunny_dat[sample(nrow(bunny_dat), nrow(bunny_dat) / 2, replace = F), c("x", "y", "input_noise_1", "input_noise_2", "input_noise_3", "input_noise_4", "input_noise_5", "input_noise_6", "input_noise_7", "input_noise_8", "input_noise_9", "input_noise_10", "z")] sampleB <- bunny_dat[!row.names(bunny_dat) %in% rownames(sampleA), c("x", "y", "input_noise_1", "input_noise_2", "input_noise_3", "input_noise_4", "input_noise_5", "input_noise_6", "input_noise_7", "input_noise_8", "input_noise_9", "input_noise_10", "z")] linear_fit <- function(subset){ dat <- sampleA[, c(subset, "z")] lm_m <- lm(formula = z ~., data = dat, model = T) lm_predict <- predict(lm_m, newdata = sampleB) r_sq_validate <- 1 - sum((sampleB$z - lm_predict) ^ 2) / sum((sampleB$z - mean(sampleB$z)) ^ 2) print(subset) print(r_sq_validate) return(r_sq_validate) } #subset <- backward.search(attributes = names(sampleA)[1:(ncol(sampleA) - 1)], eval.fun = linear_fit) subset <- forward.search(attributes = names(sampleA)[1:(ncol(sampleA) - 1)], eval.fun = linear_fit)

結果：

 > subset <b>[1] "x" "y" "input_noise_2" "input_noise_5" "input_noise_6" "input_noise_8" "input_noise_9"</b>

ノイズ変数であることが判明しました。

訓練されたモデルを見てみましょう：

 > summary(lm_m) Call: lm(formula = z ~ ., data = dat, model = T) Residuals: Min 1Q Median 3Q Max -0.060613 -0.022650 -0.000173 0.024939 0.048544 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 0.0232453 0.0005581 41.651 < 2e-16 *** <b>x -0.0257686 0.0052998 -4.862 1.17e-06 *** y -0.1572786 0.0052585 -29.910 < 2e-16 ***</b> input_noise_2 -0.0017249 0.0027680 -0.623 0.533 input_noise_5 -0.0027391 0.0027848 -0.984 0.325 input_noise_6 0.0032417 0.0027907 1.162 0.245 input_noise_8 0.0044998 0.0027723 1.623 0.105 input_noise_9 0.0006839 0.0027808 0.246 0.806 --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 0.02742 on 17965 degrees of freedom Multiple R-squared: 0.04937, Adjusted R-squared: 0.049 F-statistic: 133.3 on 7 and 17965 DF, p-value: < 2.2e-16

実際には、元の入力と方程式の自由項のみが統計的有意性を受け入れていることがわかります。

次に、貪欲な変数の除外を行います。

コード

 subset <- backward.search(attributes = names(sampleA)[1:(ncol(sampleA) - 1)], eval.fun = linear_fit) #subset <- forward.search(attributes = names(sampleA)[1:(ncol(sampleA) - 1)], eval.fun = linear_fit)

結果：

 > subset <b>[1] "x" "y" "input_noise_2" "input_noise_5" "input_noise_6" "input_noise_8" "input_noise_9"</b>

モデルにはノイズも含まれていました。

訓練されたモデルを見てみましょう：

 > summary(lm_m) Call: lm(formula = z ~ ., data = dat, model = T) Residuals: Min 1Q Median 3Q Max -0.060613 -0.022650 -0.000173 0.024939 0.048544 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 0.0232453 0.0005581 41.651 < 2e-16 *** <b>x -0.0257686 0.0052998 -4.862 1.17e-06 *** y -0.1572786 0.0052585 -29.910 < 2e-16 ***</b> input_noise_2 -0.0017249 0.0027680 -0.623 0.533 input_noise_5 -0.0027391 0.0027848 -0.984 0.325 input_noise_6 0.0032417 0.0027907 1.162 0.245 input_noise_8 0.0044998 0.0027723 1.623 0.105 input_noise_9 0.0006839 0.0027808 0.246 0.806 --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 0.02742 on 17965 degrees of freedom Multiple R-squared: 0.04937, Adjusted R-squared: 0.049 F-statistic: 133.3 on 7 and 17965 DF, p-value: < 2.2e-16

同様に、モデル内では元の入力のみが重要であることがわかります。

変数XおよびYのみでモデルをトレーニングすると、次のようになります。

 > print(subset) <b>[1] "x" "y"</b> > print(r_sq_validate) <b>[1] 0.05185492</b> > summary(lm_m) Call: lm(formula = z ~ ., data = dat, model = T) Residuals: Min 1Q Median 3Q Max -0.059884 -0.022653 -0.000209 0.024955 0.048238 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 0.0233808 0.0005129 45.590 < 2e-16 *** <b>x -0.0257813 0.0052995 -4.865 1.15e-06 *** y -0.1573098 0.0052576 -29.920 < 2e-16 ***</b> --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 0.02742 on 17970 degrees of freedom Multiple R-squared: 0.04908, Adjusted R-squared: 0.04898 F-statistic: 463.8 on 2 and 17970 DF, p-value: < 2.2e-16

事実、検証では、ノイズ変数をオフにしたときのR ^ 2が高くなりました。

奇妙な結果！おそらく、データ構造により、ノイズはモデルに悪影響を与えません。

しかし、予測変数の相互作用を考慮に入れようとはまだしていません。

コード

 lm_m <- lm(formula = z ~ x * y, data = dat, model = T)

それはかなりうまくいった：

 > summary(lm_m) Call: lm(formula = z ~ x * y, data = dat, model = T) Residuals: Min 1Q Median 3Q Max -0.057761 -0.023067 -0.000119 0.024762 0.049747 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 0.0196766 0.0006545 30.062 <2e-16 *** x -0.1513484 0.0148113 -10.218 <2e-16 *** y -0.1084295 0.0075183 -14.422 <2e-16 *** x:y 1.3771299 0.1517363 9.076 <2e-16 *** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 0.02736 on 17969 degrees of freedom Multiple R-squared: 0.05342, Adjusted R-squared: 0.05327 F-statistic: 338.1 on 3 and 17969 DF, p-value: < 2.2e-16

XとYの相互作用は重要です。検証に関するR ^ 2はどうですか？

 > lm_predict <- predict(lm_m, + newdata = sampleB) > 1 - sum((sampleB$z - lm_predict) ^ 2) / sum((sampleB$z - mean(sampleB$z)) ^ 2) <b>[1] 0.05464066</b>

これは私たちが見た中で最高の値です。残念ながら、それはフィットネス関数に規定されていない相互作用オプションであり、この入力の組み合わせを逃しました。

実験＃2：重要度を評価する線形関数を使用した入力のサブセットの貪欲検索（埋め込みオプションはフィットネス関数として使用されます-トレーニングサンプルのトレーニングモデルのf統計量）。

コード

 linear_fit_f <- function(subset){ dat <- sampleA[, c(subset, "z")] lm_m <- lm(formula = z ~., data = dat, model = T) print(subset) print(summary(lm_m)$fstatistic[[1]]) return(summary(lm_m)$fstatistic[[1]]) } #subset <- backward.search(attributes = names(sampleA)[1:(ncol(sampleA) - 1)], eval.fun = linear_fit_f) subset <- forward.search(attributes = names(sampleA)[1:(ncol(sampleA) - 1)], eval.fun = linear_fit_f)

変数の順次包含の結果は、1つの予測子Yのみです。そのため、F統計は最大化されました。つまり、この変数は非常に重要です。しかし、何らかの理由で変数Xは忘れられています。

そして、変数の順次除外。

結果は同様です-1つの変数のみがYです。

F-Statistic多変数モデルを最大化すると、すべてのノイズがオーバーボードであり、モデルがロバストであることが判明しました。検証の決定係数は、実験番号1の最良のモデルとほぼ同じです。

 > r_sq_validate <b>[1] 0.05034534</b>

実験3：ピアソン相関係数を使用して予測変数の個々の有意性を交互に評価します（このオプションは最も単純で、相互作用を考慮せず、フィットネス関数も単純です-線形関係のみを評価します）。

コード

 correlation_arr <- data.frame() for (i in 1:12){ correlation_arr[i, 1] <- colnames(sampleA)[i] correlation_arr[i, 2] <- cor(sampleA[, i], sampleA[, 'z']) }

結果：

 > correlation_arr V1 V2 <b>1 x 0.0413782832 2 y -0.2187061876</b> 3 input_noise_1 -0.0097719425 4 input_noise_2 -0.0019297383 5 input_noise_3 0.0002143946 6 input_noise_4 -0.0142325764 7 input_noise_5 -0.0048206943 8 input_noise_6 0.0090877674 9 input_noise_7 -0.0152897433 10 input_noise_8 0.0143477495 11 input_noise_9 0.0027560459 12 input_noise_10 -0.0079526578

最も高い相関はZとYの間であり、2番目はXです。ただし、Xの相関は顕著ではなく、各変数の相関係数とゼロの差の有意性の統計的検定が必要です。

一方、実行された3つの実験すべてで、予測子の相互作用（X * Y）をまったく考慮しませんでした。これは、ユニットの有意性の評価または方程式への予測変数の線形包含が明確な答えを与えないという事実を説明できます。

そのような実験者：

 > cor(sampleA$x * sampleA$y, sampleA$z) <b>[1] 0.1211382</b>

XとYの相互作用がZとかなり強く相関していることを示しています。

実験番号4：マシンに組み込まれたアルゴリズムによる予測子の重要性の評価（貪欲検索の変形とGBMの入力の重要性の埋め込みフィットネス関数）。

Gradient Boosted Trees（gbm）をトレーニングし、変数の重要性を調べます。 GBMの使用に関する詳細な記事： 勾配ブースティングマシン、チュートリアル。

天井から学習パラメーターを取得し、非常に低い学習速度を設定して、強い再トレーニングを避けます。決定木は貪欲であり、多くのモデルを追加してモデルを改善することは、観測値と入力をサンプリングすることによって達成されることに注意してください。

コード

 library(gbm) gbm_dat <- bunny_dat[, c("x", "y", "input_noise_1", "input_noise_2", "input_noise_3", "input_noise_4", "input_noise_5", "input_noise_6", "input_noise_7", "input_noise_8", "input_noise_9", "input_noise_10", "z")] gbm_fit <- gbm(formula = z ~., distribution = "gaussian", data = gbm_dat, n.trees = 500, interaction.depth = 12, n.minobsinnode = 100, shrinkage = 0.0001, bag.fraction = 0.9, train.fraction = 0.7, n.cores = 6) gbm.perf(object = gbm_fit, plot.it = TRUE, oobag.curve = F, overlay = TRUE) summary(gbm_fit)

結果：

 > summary(gbm_fit) var rel.inf <b>yy 69.7919 xx 30.2081</b> input_noise_1 input_noise_1 0.0000 input_noise_2 input_noise_2 0.0000 input_noise_3 input_noise_3 0.0000 input_noise_4 input_noise_4 0.0000 input_noise_5 input_noise_5 0.0000 input_noise_6 input_noise_6 0.0000 input_noise_7 input_noise_7 0.0000 input_noise_8 input_noise_8 0.0000 input_noise_9 input_noise_9 0.0000 input_noise_10 input_noise_10 0.0000

このアプローチはタスクに完全に対応し、非ノイズ入力を強調し、他のすべての入力をまったく重要ではありませんでした。

さらに、この実験の設定は非常に高速であり、すべてがほとんどそのままで機能することに注意してください。最適なトレーニングパラメーターを取得するための交差検証を含む、この実験のより綿密な計画はより複雑ですが、実稼働環境で実際のモデルを準備するときにこれを行う必要があります。

実験番号5：重要度を推定する線形関数を使用した確率的検索を使用して予測変数の重要度を推定します（これは入力空間での貪欲でない検索であり、ラッパーオプションはフィットネス関数として使用されます-検証サンプルでトレーニング済みモデルの決定係数を推定します）。

今回、学習線形モデルには、予測子間のペアワイズ相互作用が含まれます。

コード

 ### simulated annealing search with linear model interactions stats library(scales) library(GenSA) sampleA <- bunny_dat[sample(nrow(bunny_dat), nrow(bunny_dat) / 2, replace = F), c("x", "y", "input_noise_1", "input_noise_2", "input_noise_3", "input_noise_4", "input_noise_5", "input_noise_6", "input_noise_7", "input_noise_8", "input_noise_9", "input_noise_10", "z")] sampleB <- bunny_dat[!row.names(bunny_dat) %in% rownames(sampleA), c("x", "y", "input_noise_1", "input_noise_2", "input_noise_3", "input_noise_4", "input_noise_5", "input_noise_6", "input_noise_7", "input_noise_8", "input_noise_9", "input_noise_10", "z")] #calculate parameters predictor_number <- dim(sampleA)[2] - 1 sample_size <- dim(sampleA)[1] par_v <- runif(predictor_number, min = 0, max = 1) par_low <- rep(0, times = predictor_number) par_upp <- rep(1, times = predictor_number) ############### the fitness function sa_fit_f <- function(par){ indexes <- c(1:predictor_number) for (i in 1:predictor_number){ if (par[i] >= threshold) { indexes[i] <- i } else { indexes[i] <- 0 } } local_predictor_number <- 0 for (i in 1:predictor_number){ if (indexes[i] > 0) { local_predictor_number <- local_predictor_number + 1 } } if (local_predictor_number > 0) { sampleAf <- as.data.frame(sampleA[, c(indexes[], dim(sampleA)[2])]) lm_m <- lm(formula = z ~ .^2, data = sampleAf, model = T) lm_predict <- predict(lm_m, newdata = sampleB) r_sq_validate <- 1 - sum((sampleB$z - lm_predict) ^ 2) / sum((sampleB$z - mean(sampleB$z)) ^ 2) } else { r_sq_validate <- 0 } return(-r_sq_validate) } #stimating threshold for variable inclusion threshold <- 0.5 # do it simply #run feature selection start <- Sys.time() sao <- GenSA(par = par_v, fn = sa_fit_f, lower = par_low, upper = par_upp , control = list( #maxit = 10 max.time = 300 , smooth = F , simple.function = F)) trace_ff <- data.frame(sao$trace)$function.value plot(trace_ff, type = "l") percent(- sao$value) final_vector <- c((sao$par >= threshold), T) names(sampleA)[final_vector] final_sample <- as.data.frame(sampleA[, final_vector]) Sys.time() - start # check model lm_m <- lm(formula = z ~ .^2, data = sampleA[, final_vector], model = T) summary(lm_m)

どうしたの？

 <b>[1] "5.53%"</b> > final_vector <- c((sao$par >= threshold), T) > names(sampleA)[final_vector] <b>[1] "x" "y" "input_noise_7" "input_noise_8" "input_noise_9" "z" </b> > summary(lm_m) Call: lm(formula = z ~ .^2, data = sampleA[, final_vector], model = T) Residuals: Min 1Q Median 3Q Max -0.058691 -0.023202 -0.000276 0.024953 0.050618 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 0.0197777 0.0007776 25.434 <2e-16 *** <b>x -0.1547889 0.0154268 -10.034 <2e-16 *** y -0.1148349 0.0085787 -13.386 <2e-16 ***</b> input_noise_7 -0.0102894 0.0071871 -1.432 0.152 input_noise_8 -0.0013928 0.0071508 -0.195 0.846 input_noise_9 0.0026736 0.0071910 0.372 0.710 <b>x:y 1.3098676 0.1515268 8.644 <2e-16 ***</b> x:input_noise_7 0.0352997 0.0709842 0.497 0.619 x:input_noise_8 0.0653103 0.0714883 0.914 0.361 x:input_noise_9 0.0459939 0.0716704 0.642 0.521 y:input_noise_7 0.0512392 0.0710949 0.721 0.471 y:input_noise_8 0.0563148 0.0707809 0.796 0.426 y:input_noise_9 -0.0085022 0.0710267 -0.120 0.905 input_noise_7:input_noise_8 0.0129156 0.0374855 0.345 0.730 input_noise_7:input_noise_9 0.0519535 0.0376869 1.379 0.168 input_noise_8:input_noise_9 0.0128397 0.0379640 0.338 0.735 --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 0.0274 on 17957 degrees of freedom Multiple R-squared: 0.05356, Adjusted R-squared: 0.05277 F-statistic: 67.75 on 15 and 17957 DF, p-value: < 2.2e-16

見逃していることがわかります。ノイズが含まれています。

ご覧のとおり、検証用の決定係数の最適値は、ノイズ変数を含めることで達成されました。さらに、検索アルゴリズムの収束は徹底的です：

フィットネス関数を変更して、検索方法を保存してみましょう。

実験6：重要度を推定する線形関数を使用した確率的検索を使用して予測子の重要度を評価します（これは入力空間での欲張りでない検索であり、適合度関数はモデル係数に対応するp値が埋め込まれています）。

モデルに含まれる係数の平均p値が最小になるような予測子のセットを選択します。

コード

 # fittness based on p-values sa_fit_f2 <- function(par){ indexes <- c(1:predictor_number) for (i in 1:predictor_number){ if (par[i] >= threshold) { indexes[i] <- i } else { indexes[i] <- 0 } } local_predictor_number <- 0 for (i in 1:predictor_number){ if (indexes[i] > 0) { local_predictor_number <- local_predictor_number + 1 } } if (local_predictor_number > 0) { sampleAf <- as.data.frame(sampleA[, c(indexes[], dim(sampleA)[2])]) lm_m <- lm(formula = z ~ .^2, data = sampleAf, model = T) mean_val <- mean(summary(lm_m)$coefficients[, 4]) } else { mean_val <- 1 } return(mean_val) } #stimating threshold for variable inclusion threshold <- 0.5 # do it simply #run feature selection start <- Sys.time() sao <- GenSA(par = par_v, fn = sa_fit_f2, lower = par_low, upper = par_upp , control = list( #maxit = 10 max.time = 60 , smooth = F , simple.function = F)) trace_ff <- data.frame(sao$trace)$function.value plot(trace_ff, type = "l") percent(- sao$value) final_vector <- c((sao$par >= threshold), T) names(sampleA)[final_vector] final_sample <- as.data.frame(sampleA[, final_vector]) Sys.time() - start

結果：

 > percent(- sao$value) <b>[1] "-4.7e-208%"</b> > final_vector <- c((sao$par >= threshold), T) > names(sampleA)[final_vector] <b>[1] "y" "z"</b>

今回はすべてがうまくいきました。元の予測値のみが選択されました。p値が非常に小さいためです。

アルゴリズムの収束は60秒で良好です：

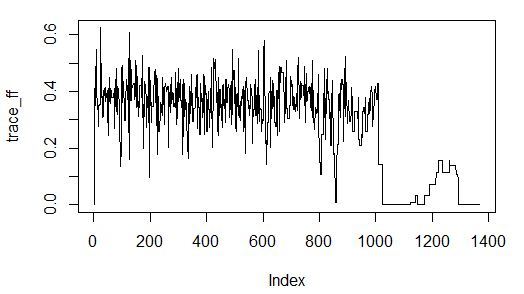実験7：学習済みモデルの品質による重要度の評価を伴う貪欲検索を使用して予測子の重要度を評価します（これは入力空間での貪欲な検索であり、適合度関数はラッパーです。これは、検証モデルでブーストされた決定木の決定係数に対応します）。

コード

 ### greedy search with wrapper GBM validation fitness library(FSelector) library(gbm) sampleA <- bunny_dat[sample(nrow(bunny_dat), nrow(bunny_dat) / 2, replace = F), c("x", "y", "input_noise_1", "input_noise_2", "input_noise_3", "input_noise_4", "input_noise_5", "input_noise_6", "input_noise_7", "input_noise_8", "input_noise_9", "input_noise_10", "z")] sampleB <- bunny_dat[!row.names(bunny_dat) %in% rownames(sampleA), c("x", "y", "input_noise_1", "input_noise_2", "input_noise_3", "input_noise_4", "input_noise_5", "input_noise_6", "input_noise_7", "input_noise_8", "input_noise_9", "input_noise_10", "z")] gbm_fit <- function(subset){ dat <- sampleA[, c(subset, "z")] gbm_fit <- gbm(formula = z ~., distribution = "gaussian", data = dat, n.trees = 50, interaction.depth = 10, n.minobsinnode = 100, shrinkage = 0.1, bag.fraction = 0.9, train.fraction = 1, n.cores = 7) gbm_predict <- predict(gbm_fit, newdata = sampleB, n.trees = 50) r_sq_validate <- 1 - sum((sampleB$z - gbm_predict) ^ 2) / sum((sampleB$z - mean(sampleB$z)) ^ 2) print(subset) print(r_sq_validate) return(r_sq_validate) } subset <- backward.search(attributes = names(sampleA)[1:(ncol(sampleA) - 1)], eval.fun = gbm_fit) subset <- forward.search(attributes = names(sampleA)[1:(ncol(sampleA) - 1)], eval.fun = gbm_fit)

予測子を貪欲に含む結果：

 > subset <b>[1] "x" "y"</b> > r_sq_validate <b>[1] 0.2363794</b>

ポイントを打つ！

予測子の貪欲な除外の結果：

 > subset <b> [1] "x" "y" "input_noise_1" "input_noise_2" "input_noise_3" "input_noise_4" "input_noise_5" "input_noise_6" "input_noise_7" [10] "input_noise_9" "input_noise_10"</b> > r_sq_validate <b>[1] 0.2266737</b>

悪化しています。モデルにノイズ予測子を含めても、検証時の予測の品質は大幅に低下しませんでした。また、これには説明があります。ランダム決定フォレストには正規化機能が組み込まれており、学習プロセスで非情報入力を無視できます。

これで、標準的な方法を使用してIPRに関する実験のセクションを完了します。そして次のセクションでは、統計的に信頼でき、その仕事をうまく行っている、情報メトリックに基づいた方法の実用的なアプリケーションを正当化して示します。

3）IPRの適応度関数を構築するための情報理論の使用。

このセクションの重要な質問は、依存の概念をどのように説明し、情報理論的な意味でそれを定式化するかです。

出所

情報エントロピーの概念から始める必要があります。エントロピー（シャノン）は不確実性の同義語です。ランダム変数の値について不確実であるほど、エントロピー（情報の別の同義語）がこの変数の実現になります。コインフリップの例を考慮すると、他のすべてのコインオプションの対称コインは、次のフリップ結果で最大の不確実性があるため、最大のエントロピーを持ちます。

シャノンエントロピーの式：

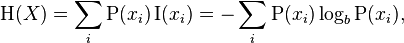
中毒とは何ですか？

コインを数回ひっくり返すと仮定します。前のスローの結果を見た後、スローの次の結果に関する不確実性が減少したと言えますか？

頭を落とした後、2/3の確率でイーグルと着陸するコインがあるとします。逆に、イーグルを失った後、2/3の確率で着陸します。この場合、ワシおよび尾の損失の無条件の頻度は50/50のままです。

そのようなコインの場合、ワシの損失後、尾の損失の頻度は1/2でなくなり、その逆も同様です。そのため、スローの次の結果についての不確実性は減少しました（50/50はもはや予想されません）。

依存の現象を理解するために、確率論では独立性を次のように定義していることを思い出してください。

p（x、y）== p（x）* p（y）

したがって、イベントの共同実現の確率は、イベント自体の実現の確率の積に等しくなります。

これが観察される場合、イベントは数学的な意味で独立しています。もし

p（x、y）！= p（x）* p（y）

その場合、イベントは数学的に独立ではありません。

同じ原理が、情報理論における2つ（またはそれ以上）の確率変数間の関係を測定するための公式の基礎になっています。

ここでは、依存関係は確率的な意味で理解されることを強調します。因果関係の分析には、より包括的なレビューが必要です。これには、誤った相関関係と冗長性の分析（相互情報の使用による）と、研究対象のオブジェクトに関する専門知識の魅力の両方が含まれます。

相互情報

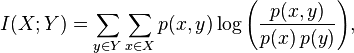
相互情報はエントロピーによっても導出できます。

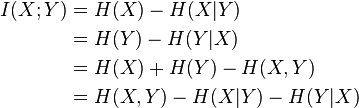
簡単な言葉で言えば、相互情報量は、予測変数（または複数の変数）がある場合にシステムから出るエントロピー（不確実性）の量です。たとえば、ランダム変数のエントロピーは3ビットです。相互情報は2ビットです。これは、ランダム変数の実装に関する不確実性が2/3までに予測子の存在によって補償されることを意味します。

相互情報には、次のプロパティがあります。

対称性
離散変数と連続変数に対して定義できます
XとYが独立している場合は消えます
2つの変数が互いに完全に決定する場合、相互情報の正規化された測定値は1になります。

相互情報は、次のように定式化された、依存の理想的な尺度のいくつかの要件を満たしています。

Granger、C、E。Maasoumi e J. Racine、「非線形プロセスの可能性がある依存メトリック」、Journal of Time Series Analysis 25、2004、649-669。

この測定を適用するときに知っておくと便利な相互情報のプロパティ（ VI ）が1つあります。

VIは、入力および出力（予測変数および従属変数）のエントロピー値のうち小さい方に等しい最大値に到達できます。

つまり、入力変数のエントロピーが10ビットで、出力のビット数が3ビットの場合、入力変数が出力を送信できる最大情報は3ビットです。これは、そのようなシステムで使用できる最大のVIです。

別のオプションは、入力変数が3ビットのエントロピーを持ち、出力が10ビットを持つことです。入力が出力に伝えることができる情報の最大値は3ビットであり、これはVIの可能な最大値です。

VIの値を従属変数のエントロピーで除算すると、範囲[0、1]の値が得られます。これは、相関係数と同様に、値のスケールを考慮せずに、入力変数が従属変数を決定する方法を示します。

VIを使用することが望ましいという多くの議論がありますが、多くのトレードオフが伴います。

この方法では、任意の次元の空間で任意の形式（線形および非線形）の依存関係を見つけることができます。
合計または個々の情報の内容が統計的に有意である場合、このメソッドはすべての入力変数を除外します。
この方法の弱点は、VIメトリックの数値的に計算された分位数を適用した後、統計ノイズのレベルをほとんど超えない弱い依存関係が研究者の目から隠されるという事実です。
少数の重要な離散入力変数を使用して、研究者は、見つかった依存関係の解釈を可能にする人間が判読できる一連のルールを構築できます。
( random forest busting machines), « » , , ;
, , -, ;
, , , .

.

, , . , , , .

— (Multiinformation) (Total Correlation).

ソース：

:

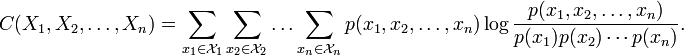
Watanabe S (1960). Information theoretical analysis of multivariate correlation, IBM Journal of Research and Development 4, 66–82

( ) , . , ( 1 n) ( 1 m), . , - .

, .

, , . :

1) . , — , , , — . , , 2. , , .
2) . , , . , , , — .
3) . , .

.

, , :

, . . , . ., , 1973 — 512 .

.. — « ».

, .

, , , , .

, n N.

. , .

100 .

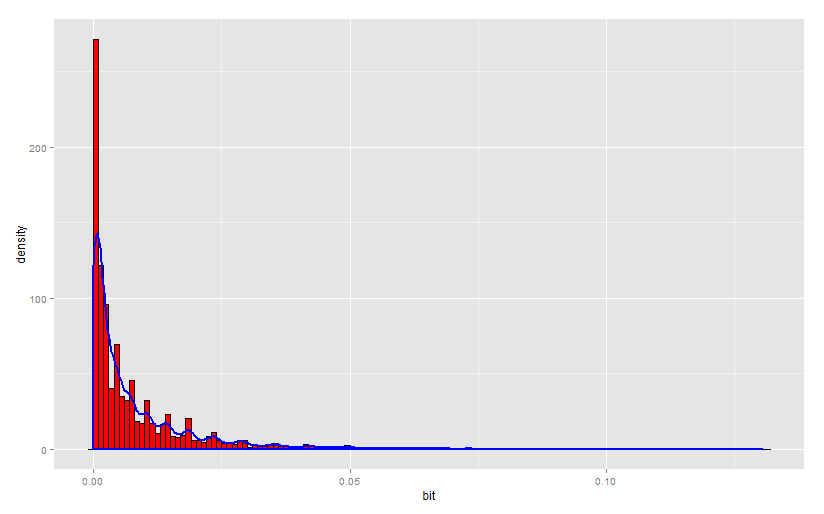
1000 .

, , .

, , . , . .:

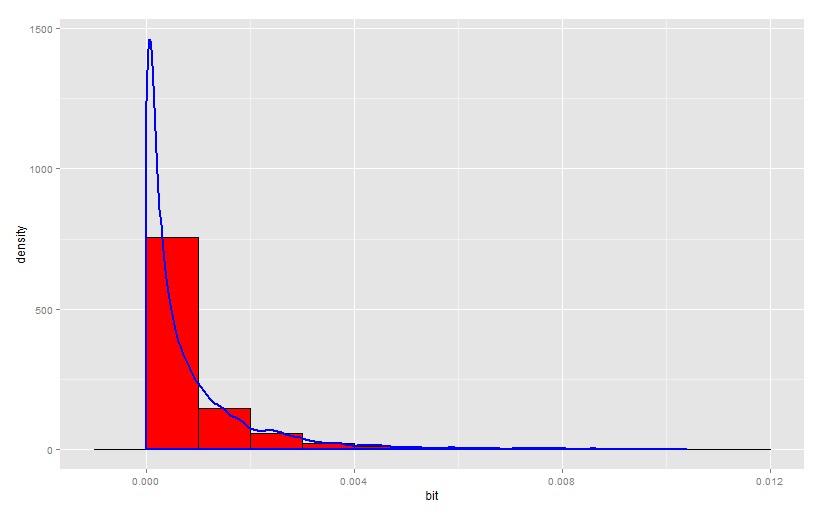
1.
2.

, , . . , ( ). , .

, .

. . , , . .

( ), .

. . , , , . , 1 000 51% , - . . .

- .

) .
) , , , ( ) « » .
) numeric , [0, 1] (0) (1) — SA.
) , , -, .
) - ; (, 0.9) .
) . より多くの、より良い。
) , .

«» . — , :

optim_var_num < — log(x = sample_size / 100, base = round(mean_levels, 0))

, , , , , n , n 100. , , , .

, , .

, , ( ), :

threshold < — 1 — optim_var_num / predictor_number

, . .

, : , .

17 973 , 12 , 5 . , 3,226.

, 0,731.

?

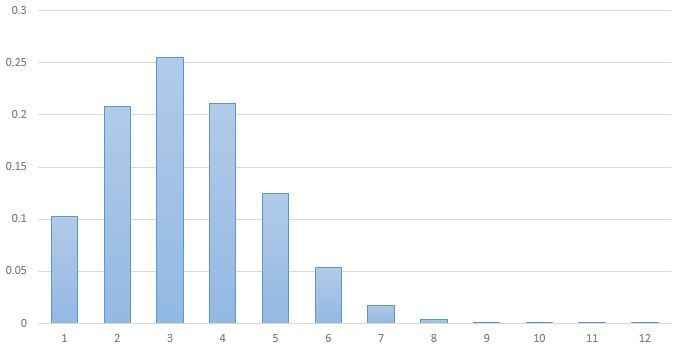
3 . , 5 ^ 3,226 178 , 100 .

.

№8 , () ( , - — ).

0,9 ( ) 10 -, 1 1 ( ). 10 .

コード

 ############## simlated annelaing search with mutual information fitness function library(infotheo) # measured in nats, converted to bits library(scales) library(GenSA) sampleA <- bunny_dat[sample(nrow(bunny_dat), nrow(bunny_dat) / 2, replace = F), c("x", "y", "input_noise_1", "input_noise_2", "input_noise_3", "input_noise_4", "input_noise_5", "input_noise_6", "input_noise_7", "input_noise_8", "input_noise_9", "input_noise_10", "z")] sampleB <- bunny_dat[!row.names(bunny_dat) %in% rownames(sampleA), c("x", "y", "input_noise_1", "input_noise_2", "input_noise_3", "input_noise_4", "input_noise_5", "input_noise_6", "input_noise_7", "input_noise_8", "input_noise_9", "input_noise_10", "z")] # discretize all variables dat <- sampleA disc_levels <- 5 for (i in 1:13){ naming <- paste(names(dat[i]), 'discrete', sep = "_") dat[, eval(naming)] <- discretize(dat[, eval(names(dat[i]))], disc = "equalfreq", nbins = disc_levels)[,1] } sampleA <- dat[, 14:26] #calculate parameters predictor_number <- dim(sampleA)[2] - 1 sample_size <- dim(sampleA)[1] par_v <- runif(predictor_number, min = 0, max = 1) par_low <- rep(0, times = predictor_number) par_upp <- rep(1, times = predictor_number) #load functions to memory shuffle_f_inp <- function(x = data.frame(), iterations_inp, quantile_val_inp){ mutins <- c(1:iterations_inp) for (count in 1:iterations_inp){ xx <- data.frame(1:dim(x)[1]) for (count1 in 1:(dim(x)[2] - 1)){ y <- as.data.frame(x[, count1]) y$count <- sample(1 : dim(x)[1], dim(x)[1], replace = F) y <- y[order(y$count), ] xx <- cbind(xx, y[, 1]) } mutins[count] <- multiinformation(xx[, 2:dim(xx)[2]]) } quantile(mutins, probs = quantile_val_inp) } shuffle_f <- function(x = data.frame(), iterations, quantile_val){ height <- dim(x)[1] mutins <- c(1:iterations) for (count in 1:iterations){ x$count <- sample(1 : height, height, replace = F) y <- as.data.frame(c(x[dim(x)[2] - 1], x[dim(x)[2]])) y <- y[order(y$count), ] x[dim(x)[2]] <- NULL x[dim(x)[2]] <- NULL x$dep <- y[, 1] rm(y) receiver_entropy <- entropy(x[, dim(x)[2]]) received_inf <- mutinformation(x[, 1 : dim(x)[2] - 1], x[, dim(x)[2]]) corr_ff <- received_inf / receiver_entropy mutins[count] <- corr_ff } quantile(mutins, probs = quantile_val) } ############### the fitness function fitness_f <- function(par){ indexes <- c(1:predictor_number) for (i in 1:predictor_number){ if (par[i] >= threshold) { indexes[i] <- i } else { indexes[i] <- 0 } } local_predictor_number <- 0 for (i in 1:predictor_number){ if (indexes[i] > 0) { local_predictor_number <- local_predictor_number + 1 } } if (local_predictor_number > 1) { sampleAf <- as.data.frame(sampleA[, c(indexes[], dim(sampleA)[2])]) pred_entrs <- c(1:local_predictor_number) for (count in 1:local_predictor_number){ pred_entrs[count] <- entropy(sampleAf[count]) } max_pred_ent <- sum(pred_entrs) - max(pred_entrs) pred_multiinf <- multiinformation(sampleAf[, 1:dim(sampleAf)[2] - 1]) pred_multiinf <- pred_multiinf - shuffle_f_inp(sampleAf, iterations_inp, quantile_val_inp) if (pred_multiinf < 0){ pred_multiinf <- 0 } pred_mult_perc <- pred_multiinf / max_pred_ent inf_corr_val <- shuffle_f(sampleAf, iterations, quantile_val) receiver_entropy <- entropy(sampleAf[, dim(sampleAf)[2]]) received_inf <- mutinformation(sampleAf[, 1:local_predictor_number], sampleAf[, dim(sampleAf)[2]]) if (inf_corr_val - (received_inf / receiver_entropy) < 0){ fact_ff <- (inf_corr_val - (received_inf / receiver_entropy)) * (1 - pred_mult_perc) } else { fact_ff <- inf_corr_val - (received_inf / receiver_entropy) } } else if (local_predictor_number == 1) { sampleAf<- as.data.frame(sampleA[, c(indexes[], dim(sampleA)[2])]) inf_corr_val <- shuffle_f(sampleAf, iterations, quantile_val) receiver_entropy <- entropy(sampleAf[, dim(sampleAf)[2]]) received_inf <- mutinformation(sampleAf[, 1:local_predictor_number], sampleAf[, dim(sampleAf)[2]]) fact_ff <- inf_corr_val - (received_inf / receiver_entropy) } else { fact_ff <- 0 } return(fact_ff) } ########## estimating threshold for variable inclusion iterations = 10 quantile_val = 0.9 iterations_inp = 1 quantile_val_inp = 1 levels_arr <- numeric() for (i in 1:predictor_number){ levels_arr[i] <- length(unique(sampleA[, i])) } mean_levels <- mean(levels_arr) optim_var_num <- log(x = sample_size / 100, base = round(mean_levels, 0)) if (optim_var_num / predictor_number < 1){ threshold <- 1 - optim_var_num / predictor_number } else { threshold <- 0.5 } #run feature selection start <- Sys.time() sao <- GenSA(par = par_v, fn = fitness_f, lower = par_low, upper = par_upp , control = list( #maxit = 10 max.time = 300 , smooth = F , simple.function = F)) trace_ff <- data.frame(sao$trace)$function.value plot(trace_ff, type = "l") percent(- sao$value) final_vector <- c((sao$par >= threshold), T) names(sampleA)[final_vector] final_sample <- as.data.frame(sampleA[, final_vector]) Sys.time() - start

結果：

 > percent(- sao$value) <b>[1] "18.1%"</b> > final_vector <- c((sao$par >= threshold), T) > names(sampleA)[final_vector] <b>[1] "x_discrete" "y_discrete" "input_noise_2_discrete" "z_discrete" </b> > final_sample <- as.data.frame(sampleA[, final_vector]) > > Sys.time() - start Time difference of 10.00453 mins

ほとんど起こった。 . — .

20 , - 1 .

結果：

 > percent(- sao$value) <b><b>[1] "18.2%"</b></b> > final_vector <- c((sao$par >= threshold), T) > names(sampleA)[final_vector] <b><b>[1] "x_discrete" "y_discrete" "input_noise_1_discrete" </b>"z_discrete" </b> > final_sample <- as.data.frame(sampleA[, final_vector]) > > Sys.time() - start Time difference of 20.00585 mins

— .

18% . .

( ):

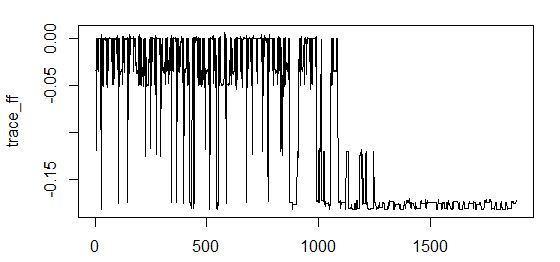Minimum-redundancy-maximum-relevance (mRMR)

. :

«Feature selection based on mutual information: criteria of max-dependency, max-relevance, and min-redundancy,»
Hanchuan Peng, Fuhui Long, and Chris Ding
IEEE Transactions on Pattern Analysis and Machine Intelligence,
Vol. 27, No. 8, pp.1226-1238, 2005

, ( ) . .

() , () .

() , , , . , .

() , . , ( ).

, , , , , ( ) , . , mRMR , .

() , — limited sampling bias.

mRMR . , , , , .

.

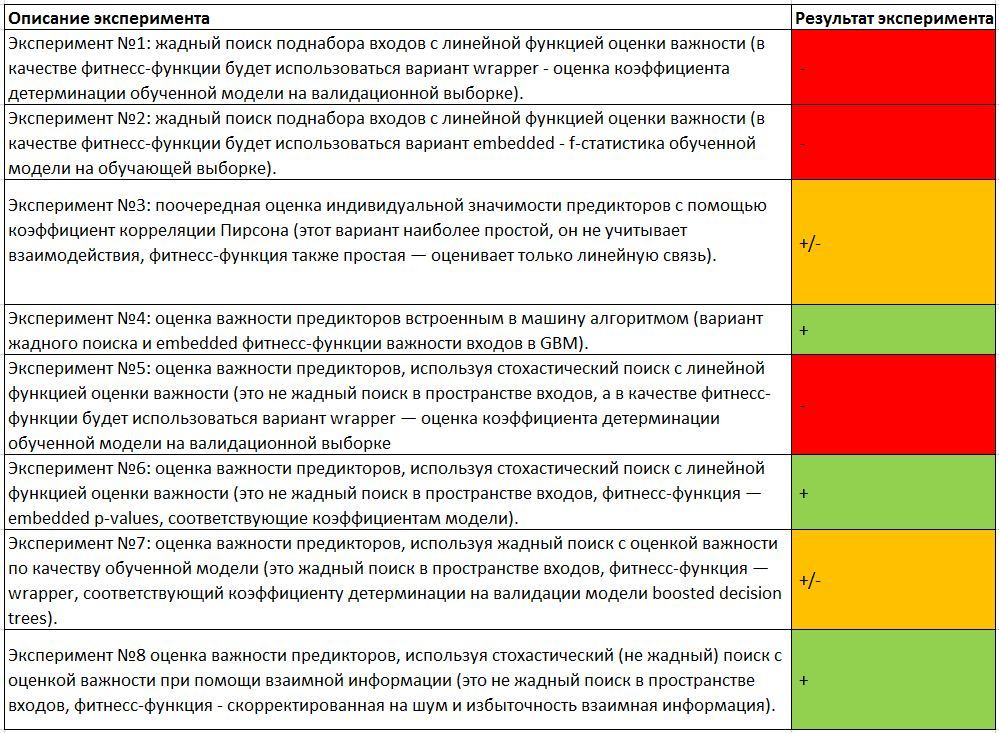
, , GBM, p-values .

, . , , , . , XY-Noise1 . , ( ), Align Technology. , , , Gradient Boosted Trees ( . ).

, , , . , , , , .

, , . . , , .

. , , , , . , .

github: Git

:

Greedy Function Approximation: A Gradient Boosting Machine by J. Friedman
, . . , . ., , 1973 — 512 .
.. — « ».
Analytical estimates of limited sampling biases in different information measures by S. Panzeri at.al.
Estimation of Entropy and Mutual Information by L. Paninski
Entropy-Based Independence Test by A. Dionísio at.al.
, , DJI, .
Measuring dependence powerfully and equitably by Y. Reshef et.al.
«Feature selection based on mutual information: criteria of max-dependency, max-relevance, and min-redundancy,» Hanchuan Peng, Fuhui Long, and Chris Ding IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 27, No. 8, pp.1226-1238, 2005
Watanabe S (1960). Information theoretical analysis of multivariate correlation, IBM Journal of Research and Development 4, 66–82
Gradient boosting machines, a tutorial.
Claude E. Shannon, Warren Weaver. The Mathematical Theory of Communication. Univ of Illinois Press, 1949

有益な特徴の選択に関する方法論的注記（特徴選択）

1）有益な機能を選択する方法と方法。

貪欲な検索アルゴリズム。

不要な検索アルゴリズム。

2）合成データに関する有益な特徴の選択に関する実験。

3）IPRの適応度関数を構築するための情報理論の使用。

このセクションの重要な質問は、依存の概念をどのように説明し、情報理論的な意味でそれを定式化するかです。

中毒とは何ですか？

相互情報

.

, .

- .

:

More articles: