ご挨拶、%ユーザー名%。 今日は、人々の興味の類似性の評価を編集するためのスクリプトを開発します。
に興味がありますか? カットをお願いします
参加する代わりに
この方法は、セットの特性の数とセットの数の間の最大の関係に対してのみ効果的に機能することに注意してください。 それ以外の場合は、この
方法を使用することをお勧めします
理論
それでは、遠くから始めましょう。 いくつかのデータセットのうち2つを想像してください。 それらを
pおよび
qと呼びます。 これらの各セットを2つの数字で特徴付けます。 次に、これらのセットを次元dimL = nの空間Lの点として表します。ここで、nは特性の数です。 この場合、2
p(p1; p2)および
q(q1; q2)メトリックd(p、q)= kを定義します。ここで、kは係数です。 2つのセットの違い。 メトリックは、これらの2点間のユークリッド距離、つまり、わかっているアンジェムのコースから定義します。
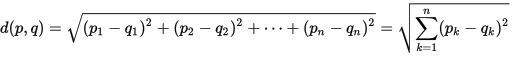
定義では、2つのセットの違いは、セットをマップするポイント間の距離になります。 次に、2つのデータセットの違いは、その方法に関するピタゴラスの定理に基づいています!
次に、2つの同一セットの場合、距離はゼロになります。
そして、これはどういう意味ですか?
例を考えてみましょう。 2つの科目を取り上げましょう。Vasya(B)とKolya(K)という名前にします。 私たちは彼らに質問します:
1)-桃がどれだけ好きか10段階評価
2)-イチゴが好きな度合いを10段階で評価する
VasyaとKolyaが同じように答えたと仮定します。 そして、明らかに、ポイント間の距離はゼロになります。つまり、これらの興味/好みのセットでは、それらは同一です。 ここで、異なる回答の場合を検討します。
Q:(1)で5、(2)で8
K:(3)で10、(2)で0
それから、KolyaとVasyaの2次元空間の点を想像できます。
(5; 8)とK(10; 0)では、それらの間の距離です。9.4を簡単に計算できます。 これが係数です。 違い。 しかし...待って、どのように解釈しますか?
見てみましょう。 セットが完全に同一の場合、最小の差はゼロです。これは理解できます。 しかし、最大値はどうですか? 私たちの飛行機でいくつかのデルタ近隣を検討してください。 ポイントの最大数は10であるため、デルタは10に等しくなります。つまり、ピタゴラスの定理sqrt(100 + 100)= 14.14によると、これはデータセットが反対と見なされる最大の差です。 したがって、この場合のKolyaとVasyaには、類似点よりも多くの違いがあります。
そして、なぜそれだけですか?
アプリケーションはどこにでもあります。 出会い系サイト、フリーランスサイト、求人サイトなど アンケートを作成することにより、興味と好みのマップを作成して、関係のペアを見つけることができます。 好色な、友好的な、労働、いずれか。
人々の興味をマッピングする例を実装します。 そして、私の友人を例として使用して、すぐにテストします。
このPLはそのようなアルゴリズムの実装に最も適しているため、Pythonを使用します。 まず第一に、辞書(ハッシュ/連想配列)を使用する便利さ、およびスマートな組み込みのpickleモジュールのおかげで、質問と回答を含む辞書を直接ディスクに保存して使用することができます。 伝統的に、すべてのコードは記事の最後で見ることができます。
メトリックを計算するには、次のコードを使用します。
メトリック計算def calc(nPoint): result = 0.0 print("sqrt(", end="") for key in Dictionary: print("(", Points[nPoint[0]][key], " - ", Points[nPoint[1]][key], ")^2 + ", sep="", end="") result = result + math.pow((Points[nPoint[0]][key] - Points[nPoint[1]][key]),2) print(")") result = math.sqrt(result) return result
この関数は、Pointsディクショナリにある、分析するデータセット(データセットはディクショナリのディクショナリに格納され、キーはセット番号)を表す2つの数値のタプルを取ります。
関数は係数を返します。 2つのセットの違い。
関心を「マッピング」するには、2つだけでなく、各セットを分析する必要があります。 これには機能があります:
係数生成。 各セット def GenerateMap(): print("~~~~") for i in range(1, PSize): for j in range(i + 1, PSize + 1): print(i, " and ", j, " = ", calc( (i, j) ), sep="")
この関数は、セットの関係のマップを生成し、stdoutに表示します。
人前でスクリプトをテストする
おお、それは聞こえる。 遊びましょう。 この質問リストを作成しましょう。
質問リスト1) ? (0- , 10- )
2) (0- , 10 )
3) ?(0- , 10- )
4) ?(0- , 10- )
5) ? (0- , 10 )
6) ? (0- , 10 )
7) ? (0- , 10 )
8) ? (0- , 10 )
9) ? (0, 10)
10) ? ( 0, 10)
11) (0, 10)
12) (0, 10)
13) (0, 10)
そして、データセットを作成して、各ユーザーに回答させます。 プログラムでは、pickleを介してロードされるデータセットに番号が付けられていることをすぐに言わなければなりません。 そのため、それぞれの形式で数値が表示されます(数値-数値=係数。差)。
読みやすくするために、手動で姓に再入力し、記事のランダムなものに置き換えました(全員から同意を得たわけではありません)。
マッピングを実行すると、次の結果が得られます。
排気- = 11.83
- = 12.72
- = 12.92
- = 12.88
- = 16.49
- = 9.59
- = 8.77
- = 10
- = 14.28
- = 10.34
- = 13.85
- = 12.4
- = 12.68
- = 14.93
- = 17.66
これをどのように解釈しますか? 13の質問がありました。最大ポイント数は10です
次に、ピタゴラスの定理により、13次元空間の近傍で可能な最大距離を見つけます。
sqrt(100 * 13)= 36,056
平均=最大/ 2 = 16.03
したがって、基本的には友人とより多くの共通点があることがわかります(これは論理的です)。
そして、AzarovaとPetrovaの違いの評価のみが、これら2人の友人(ガールフレンド)が係数として関心が最も異なることを示しています。 17.66に等しく、平均値を超えています。
結論の代わりに
したがって、この方法は、出会い系サイトへの関心によってユーザーをランク付けするために使用できます。 質問が多ければ多いほど、性格の比較がより正確になることがわかります。 たとえば、登録中に100の質問のアンケートを作成し、小規模なソーシャルネットワークのマップを作成しました(この方法のメモリ量はユーザーの増加に伴って直線的に増加するため)。