ファンクター（「プログラマー向けのカテゴリー理論」の本の章）

これは、プログラマシリーズのカテゴリ理論の7番目の記事です。 以前の記事はすでにHabréで公開されています。

• プログラマーのカテゴリー理論：序文
• カテゴリ：構成の本質
• 種類と機能
• 大小のカテゴリ
• カテゴリーClaysley
• 作品と副産物
• 単純な代数データ型

ファンクター

ファンクターの概念の背後には、非常にシンプルでありながら強力なアイデアがあります（どのようにハックされているように聞こえても）。 単なるカテゴリー理論は、シンプルで強力なアイデアに満ちています。 ファンクターは、カテゴリー間のマッピングです。 2つのカテゴリCとDが与えられ、ファンクターFがCのオブジェクトをDのオブジェクトにマッピングするとします-これはオブジェクトに対する関数です。 aがCからのオブジェクトである場合、 Dからの画像をF a （括弧なし）で示します。 ただし、カテゴリはオブジェクトだけでなく、それらをつなぐ射でもあります。 ファンクタは射も表示します-これは射に対する関数です。 しかし、射はランダムに表示されるのではなく、接続を維持するような方法で表示されます。 つまり、Cの射fがオブジェクトaとオブジェクトbを関連付ける場合、

f :: a -> b 

次に、Dのfの画像F fは 、 aの画像とbの画像を接続します。

 F f :: F a -> F b 

（数学表記とHaskell構文のこのような混合物が読者に理解できることを願っています。オブジェクトまたは射にファンクターを適用することで括弧を書きません。）

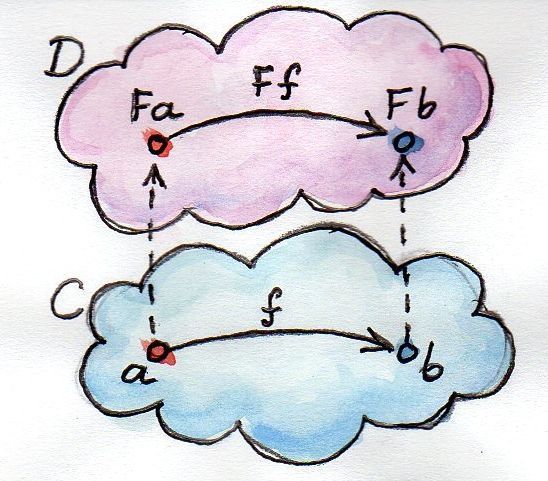
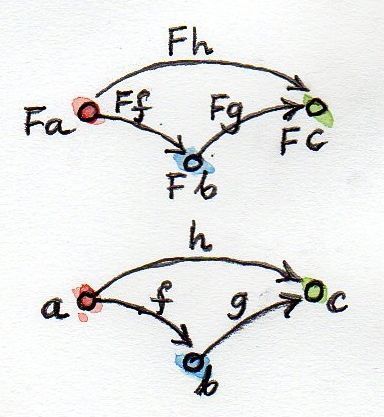
ご覧のように、ファンクターは構造を保持します。入力カテゴリで接続されていたものは、出力でも接続されます。 しかし、構造はこれに限定されません：射の合成をサポートすることも必要です。 hがfとg合成でf g ：

次に、Fの作用下の画像が画像fとgの合成であることが必要です。

 F h = F g . F f 

最後に、Cからのすべてのユニット（同一性）射がDからのユニット射にマッピングされる必要があります。

 F id(a) = id(F a) 

ここで、 id _aはオブジェクトaの単位射であり、 id _{F a}はオブジェクトF aの単位射です。

これらの条件はすべて、射として適した関数の範囲を大幅に制限することに注意してください。 ファンクターは、カテゴリーの構造を維持する必要があります。 カテゴリーを射と混ざり合ったオブジェクトのセットとして想像すると、ファンクターはこのレースの単一の糸を切る権利を持ちません。 複数のオブジェクトを組み合わせることができ、モーフィズムを1つに結び付けることができますが、結び付きを壊すことはありません。 この制限は、数学的分析の連続性の概念に似ています。 この意味で、ファンクターは「連続的」です（ただし、ファンクターの連続性にはさらに制限的な定義があります）。 他の関数と同様に、ファンクターは接着またはネストできます。 投資の側面は、ソースカテゴリがターゲットよりもはるかに小さいときに最も顕著になります。 極端な場合、最初のカテゴリはカテゴリ1で、1つのオブジェクトと1つの（単一の）射で構成されます。 カテゴリ1から他のカテゴリへのファンクタは、このカテゴリから特定のオブジェクトを選択するだけです。 ターゲットセットから要素を選択するシングルトン射との完全な類似性があります。 不合理に減少した接着面は、定数ファンクター_Δcで観察され_ます 。 ソースカテゴリの各オブジェクトをターゲットカテゴリの特定のオブジェクトcにマップし、すべての射を単一の射ID id _cにマップします。 それはブラックホールのようなもので、すべてを特異点に吸い込みます。 制限と共同制限について議論するとき、このファンクターの考察に戻ります。

プログラミングのファンクター

私たちは地球、プログラミングの世界に戻ります。 したがって、型と関数のカテゴリがあります。 このカテゴリーを自分自身にマップするファンクター、いわゆるエンドファンクターを考えてください。 型カテゴリの内機能とは何ですか？ まず、あるタイプを別のタイプにマップします。 実際、私たちはそのようなマッピングに精通しています;これらは他の型によってパラメータ化された型です。 いくつかの例を見てみましょう。

たぶんファンクター

Maybeの定義は、タイプaからMaybe aへのマッピングです。

 data Maybe a = Nothing | Just a 

重要な詳細： Maybeそれ自体は型ではなく、型コンストラクタです。 IntやBoolなどの型を引数として受け取り、別の型を返します。 Maybe 、引数なしは型に関する関数です。 しかし、 Maybeファンクターでしょうか？ （以下、プログラミングの文脈でファンクターについて話すとき、エンドファンクターはほとんど常に意味されます。）結局、ファンクターはオブジェクト（ここでは型）のマッピングだけでなく、射（ここでは関数）のマッピングでもあります。 aからbまでのすべての関数

 f :: a -> b 

Maybe bからMaybe bまでの関数を取得したいと思います。 このような関数を定義するには、2つのMaybeコンストラクターに対応する2つのケースを考慮する必要があります。 Nothingの場合、単純にNothing返します。 引数がJust場合、関数fをそのコンテンツに適用します。 そのため、 Maybeの影響下にあるfのイメージは関数です

 f' :: Maybe a -> Maybe b f' Nothing = Nothing f' (Just x) = Just (fx) 

（ところで、Haskellでは、変数名にアポストロフィを使用できます。これは、このような場合に非常に便利です。）Haskellでは、モーフィズムの表示を担当するファンクターの外観は、高次fmapによって実装されます。 Maybe次のシグネチャがあります。

 fmap :: (a -> b) -> (Maybe a -> Maybe b) 

fmapは関数を上げる（持ち上げる）とよく言われます。 sublime関数は、 Maybe値で機能します。 通常、カリー化により、このシグニチャは2つの方法で解釈できます。1つの変数の関数として、それ自体が関数(a->b)であり、関数を返す(Maybe a -> Maybe b) (a->b) (Maybe a -> Maybe b) 、または2つの変数の関数として、 Maybe bを返します：

 fmap :: (a -> b) -> Maybe a -> Maybe b 

上記に従って、 Maybe fmapを定義します。

 fmap _ Nothing = Nothing fmap f (Just x) = Just (fx) 

Maybe型コンストラクターとfmap関数がファンクターを構成していることを示すために、 fmapユニットモーフィズムと合成を保持することを証明する必要があります。 これらの声明は「機能法」と呼ばれますが、カテゴリの構造が保持されていることを単に証明するものです。

同等の変換方法

Haskellの典型的な証明手法である等価変換の方法により 、関数法則を証明します。 このメソッドは、Haskellの関数が等式のセットによって定義されているという事実に依存しています：左側は右側に等しく、両方を相互に置き換えることができます（競合を避けるために置換するときに変数の名前を変更する必要がある場合があります）。 呼び出しの代わりに関数本体を置き換える（インライン化）か、本体の代わりに関数を呼び出す（リファクタリング）ことができます。 例として恒等関数を考えます：

 id x = x 

どこかで、たとえばid yに出会えば、いつでもy （インライン化）に置き換えることができます。 一般に、式id (y + 2)などid (y + 2)に適用されるid出現は、この式(y + 2)置き換えることができます。 逆方向：式eはid e （リファクタリング）に置き換えることができます。 パターンマッチングによって定義された関数の場合、各定義を個別に使用できます。 たとえば、上記のfmap定義に従って、 fmap f NothingをNothingまたはその逆に置き換えることができます。 このアプローチを実際に検討してください。 アイデンティティを維持することから始めましょう：

 fmap id = id 

NothingとJust 2つのケースを検討する必要があります。 Nothingから始めましょう（擬似Haskellを使用して、等式の左側から右側への変換について説明します）。

  fmap id Nothing = {   fmap } Nothing = {   id } id Nothing 

2番目のステップで、反対方向のidの定義を使用して、 id Nothing代わりにid Nothingを置き換えたことに注意してください。 実際には、このような証拠は、「この場合はNothingという同じ表現で会議が真ん中になるまで、「両端から芯を燃やす」という方法によって行われます。 2番目のケースも簡単です。

  fmap id (Just x) = {   fmap } Just (id x) = {   id } Just x = {   id } id (Just x) 

fmapがコンポジションを保存することを示します：

 fmap (g . f) = fmap g . fmap f 

Nothingケースから始めましょう。

  fmap (g . f) Nothing = {   fmap } Nothing = {   fmap } fmap g Nothing = {   fmap } fmap g (fmap f Nothing) 

それではJustの時間です。

  fmap (g . f) (Just x) = {   fmap } Just ((g . f) x) = {    } Just (g (fx)) = {   fmap } fmap g (Just (fx)) = {   fmap } fmap g (fmap f (Just x)) = {    } (fmap g . fmap f) (Just x) 

C ++スタイルの副作用を持つ関数では、同等の変換方法が機能しないことを強調する価値があります。 例を考えてみましょう：

 int square(int x) { return x * x; } int counter() { static int c = 0; return c++; } double y = square(counter()); 

同等の変換方法では、 squareを展開して取得できます

 double y = counter() * counter(); 

間違いなく、そのような変換は正しくなく、式の結果を変更します。 それにもかかわらず、 squareマクロとして定義されている場合、C ++プリプロセッサーは同等の変換方法を使用して、悲惨な結果をもたらします。

たぶんまた

ファンクタはHaskellで簡単に表現できますが、一般化プログラミングと高階関数をサポートする任意の言語で記述することができます。 optionalのテンプレートタイプであるMaybeのC ++アナログを考えてみましょう。 以下に実装のスケッチを示します（完全な実装は、引数を渡すさまざまな方法、コピーセマンティクス、およびC ++リソース管理に固有のその他の問題を明示的に説明しているため、はるかに複雑です）。

 template<class T> class optional { bool _isValid; // the tag T _v; public: optional() : _isValid(false) {} // Nothing optional(T x) : _isValid(true) , _v(x) {} // Just bool isValid() const { return _isValid; } T val() const { return _v; } }; 

上記のテンプレートは、ファンクターの説明の半分であるタイプマッピングを提供します。 新しいタイプのoptional<T>各タイプTにマップしますT 次に、関数に対するアクションを説明します。

 template<class A, class B> std::function<optional<B>(optional<A>)> fmap(std::function<B(A)> f) { return [f](optional<A> opt) { if (!opt.isValid()) return optional<B>{}; else return optional<B>{ f(opt.val()) }; }; } 

これは、関数を引数として受け取り、関数を返す高階関数です。 そして、カレーなしの別のオプションがあります：

 template<class A, class B> optional<B> fmap(std::function<B(A)> f, optional<A> opt) { if (!opt.isValid()) return optional<B>{}; else return optional<B>{ f(opt.val()) }; } 

または、 optionalテンプレートメソッドとしてfmapを実装できます。 このような選択のあいまいさにより、C ++の「ファンクター」パターンの抽象化が問題になります。 ファンクタを継承するには、ファンクタをインターフェースにする必要があります（残念ながら、テンプレート関数は仮想化できません）。 それとも、無料のテンプレート関数、カレーかどうか？ C ++コンパイラは欠落している型を正しく推測できますか、または明示的に設定する必要がありますか？ 入力関数fがintをbool変換すると想像してください。 コンパイラーがタイプg決定する方法：

 auto g = fmap(f); 

特に将来、 fmapバージョンで多くのファンクターが存在する場合は？ （他のタイプのファンクターについてはすぐに知ることができます。）

型クラス

ファンクタの抽象化はHaskellでどのように実装されていますか？ 型クラスのメカニズムが使用されます。 型クラスは、単一のインターフェースをサポートする型のファミリーを定義します。 たとえば、同等性に匹敵するオブジェクトのクラスは次のように定義されます。

 class Eq a where (==) :: a -> a -> Bool 

型a 2つの引数を取り、 Boolを返す演算子(==)サポートする場合、型aはクラスEqに属すると主張します。 特定の型がEqに関連していることをHaskellに納得させるには、クラスのインスタンス （インスタンス、実装）として宣言し、実装(==)を提供する必要があります。 たとえば、そのような平面上の点の定義（2つのFloat型積）：

 data Point = Pt Float Float 

点の等価性を判断することが可能です：

 instance Eq Point where (Pt xy) == (Pt x' y') = x == x' && y == y' 

ここで、定義された演算子(==)は、2つのパターン(Pt xy)と(Pt x' y')間に挿入されています。 関数の本体は=記号の右側に配置されます。 Point Eqインスタンスとして宣言された後、 Point等しいかどうかを直接比較できます。 C ++やJavaとは異なり、 Pointを定義するときにクラスやEqインターフェイスを提供する必要はないことに注意してください-これは後で行うことができます。 Haskellで関数（および演算子）をオーバーロードするためのメカニズムは、型クラスだけであることに注意してください。 さまざまなファンクターのfmapをオーバーロードするために必要です。 微妙な点が1つあります。ファンクタは型としてではなく、型に対する関数、型コンストラクタとして定義されます。 型クラスは、 Eqの場合のように、型だけでなく、型コンストラクタのファミリーを記述する必要があります。 幸いなことに、Haskellの型クラスメカニズムは単純な型だけでなく型コンストラクターでも機能します（ PP：関数型パラダイムに従う良い例-関数型の世界においても、オブジェクトより悪くはありません ）。 Functorクラスの定義は次のとおりです。

 class Functor f where fmap :: (a -> b) -> fa -> fb 

与えられた署名を持つfmap関数がある場合、 fはFunctorであると主張します。 ここで、 fはmであり、 m と同じ種類の新しい変数と、新しい変数aおよびbです。 しかし、コンパイラはfが型コンストラクタであることを理解でき、その使用を追跡します。他の型、ここではfaおよびfb適用します。 したがって、Maybeの場合のように、ファンクターのインスタンスとして宣言するのは型コンストラクターです。

 instance Functor Maybe where fmap _ Nothing = Nothing fmap f (Just x) = Just (fx) 

Functorクラスと、インスタンスMaybeを含む多くの一般的な型の宣言がPrelude標準ライブラリに含まれていることに注意してください。

C ++のファンクター

C ++で同じアプローチを適用できますか？ 型コンストラクタはoptionalなどのテンプレートクラスに対応するため、テンプレートパラメータFを使用してfmap 2回パラメータ化する必要がありますF 次のように書かれています。

 template<template<class> F, class A, class B> F<B> fmap(std::function<B(A)>, F<A>); 

しかし、このテンプレートをさまざまなファンクターに特化するにはどうすればよいでしょうか？ 残念ながら、C ++テンプレート関数の部分的な特殊化は禁止されています。 あなたは書くことができません：

 template<class A, class B> optional<B> fmap<optional>(std::function<B(A)> f, optional<A> opt) 

代わりに、関数のオーバーロードに戻る必要があります。その結果、 fmapの元の定義に戻ります（カリー化せずに）。

 template<class A, class B> optional<B> fmap(std::function<B(A)> f, optional<A> opt) { if (!opt.isValid()) return optional<B>{}; else return optional<B>{ f(opt.val()) }; } 

この定義は機能しますが、適切なオーバーロードを行うには2番目の引数が必要です。 fmapのより一般的な定義fmap単に無視されます。

ファンクターリスト

プログラミングにおけるファンクターの重要性をよりよく理解するには、さらに例を検討してください。 別の型によってパラメーター化された型は、ファンクターの役割の候補です。 たとえば、一般化されたコンテナは、要素のタイプによってパラメータ化されます;リスト、非常に単純なコンテナを考えてください：

 data List a = Nil | Cons a (List a) 

ここには、 List型コンストラクタがあります。これは、任意の型aからList aへのマッピングです。 Listがファンクターであることを示すために、ファンクターに沿った関数のリフティングを定義する必要があります。 特定の関数a->b List a -> List b a->b List a -> List b a->b定義します。

 fmap :: (a -> b) -> (List a -> List b) 

List機能する関数は、2つのリストコンストラクターについて、それぞれ2つのケースを考慮する必要があります。 Nilの場合は些細なことですNilが返されます。空のリストから多くを絞り出すことはできません。 Consケースは、再帰に影響するため、 Consにくいです。 考えてみましょう。したがって、リストa 、関数fがaをbに変換し、リストbを取得したいとします。 当然、 fを使用して各リスト項目をaからbに変換する必要があります。 （空でない）リストが頭と尾のConsとして定義されている場合、正確に何をする必要がありますか？ fを頭に適用し、隆起した（fmapで欠けた） fを尾に適用します。 この定義は再帰的です。raisedfからraised fまでを定義します。

 fmap f (Cons xt) = Cons (fx) (fmap ft) 

fmap fの右側で、 fmap fが定義したものよりも短いリスト、つまり後者の末尾に適用されることが重要です。 より短いリストに再帰を適用するため、必然的に空のリスト、またはNilます。 しかし、すでに決定したように、 Nil fmap fはNilを与え、それにより再帰を完了します。 Consコンストラクターを使用して、新しいヘッド（ fx ）と新しいテール（ fmap ft ）を組み合わせることにより、最終結果が得られます。 その結果、ファンクタのインスタンスとしてのリストの完全な宣言は次のとおりです。

 instance Functor List where fmap _ Nil = Nil fmap f (Cons xt) = Cons (fx) (fmap ft) 

C ++に慣れている場合は、 std::vectorを検討するのが理にかなっています。これは基本的に基本的なC ++コンテナーです。 std::vectorのfmap実装は、 std::transform単なるラッパーです：

 template<class A, class B> std::vector<B> fmap(std::function<B(A)> f, std::vector<A> v) { std::vector<B> w; std::transform( std::begin(v) , std::end(v) , std::back_inserter(w) , f); return w; } 

その助けを借りて、たとえば、一連の数字を2乗することができます。

 std::vector<int> v{ 1, 2, 3, 4 }; auto w = fmap([](int i) { return i*i; }, v); std::copy( std::begin(w) , std::end(w) , std::ostream_iterator(std::cout, ", ")); 

ほとんどのC ++コンテナーは、本質的にファンクターです。 これは、 fmapプリミティブな相対であるstd::transform渡すことができる反復子の存在によって保証されます。 残念ながら、ファンクターの単純さは、イテレーターと一時変数（上記のfmap実装のように）のゴミの下で失われます。 良いニュースから-C ++に含める予定の範囲のライブラリは、その間隔、機能的な性質を大幅に明らかにします。

リーダーファンクター

ある種の直観、特にファンクタが何らかのコンテナであるということを開発したので、ここでは一見完全に異なる例です。 タイプaからaを返す関数のタイプへのマッピングを検討してください。 適切な理論レベルおよびカテゴリレベルでの機能タイプの議論にはまだ到達していませんが、プログラマとして、それらについてある程度理解しています。 Haskellでは、関数型は、型コンストラクターである矢印(->)を使用して構築されます。矢印(->)は、引数型と結果型の2つの型を取ります。 既に中置記法a->bでそれを満たしているが、括弧を使用すると接頭辞記法も使用できます。

 (->) ab 

通常の関数と同様に、m およびいくつかの引数の新しい関数を部分的に適用できます。 そして、矢印に1つの引数を与えたとき、まだ別の引数を待っています。 つまり、

 (->) a 

型コンストラクタです。 本格的なタイプa->bを取得するには、もう1つのタイプbが必要です。 したがって、矢印は、によってパラメータ化されaタイプコンストラクターのファミリ全体を定義します。 ファンクタのファミリーでもあるかどうかを調べてみましょう。 2つのパラメーターを混同しないように、それらの名前を変更して、役割を強調します。 ファンクターの以前の定義に従って、引数の型はrと呼ばれ、結果の型はaです。 したがって、コンストラクターは任意のタイプのa取り、タイプr->aマップします。 機能を正当化するために、関数a->bをr->aを受け取りr->bを返す関数に上げる必要があります。 これらはbそれぞれbとbのコンストラクタアクション(->) rによって作成されるタイプです。 これは署名fmapです：

 fmap :: (a -> b) -> (r -> a) -> (r -> b) 

関数f::a->bと関数g::r->a 、 r->b作成するg::r->aパズルのようなものが得られます。 それらを構成する方法は1つしかなく、結果はまさに必要なものです。 このようなfmap実装が判明します。

 instance Functor ((->) r) where fmap fg = f . g 

うまくいきました！ ミニマリストは、プレフィックス形式を使用してレコードを短縮できます。

 fmap fg = (.) fg 

引数を省略して、2つの関数を識別できるようになりました。

 fmap = (.) 

型コンストラクタ(->) rとfmapこのような実装の組み合わせは、「リーダー」と呼ばれます。

コンテナとしてのファンクター

プログラミングでファンクターを使用して汎用コンテナーを定義する例、または少なくともファンクターをパラメーター化する型の値を含むオブジェクトを定義する例について知りました。 関数をデータとは考えていないため、リーダーファンクターは例外のようです。 ただし、これまで見てきたように、計算がテーブルの検索に限定される場合、メモ化は関数に適用できます。 テーブルはすでにデータです。 一方、Haskellは遅延しているため、リストのような従来のコンテナーは実際には関数として実装できます。 たとえば、次のように説明できる自然数の無限リストを見てください。

 nats :: [Integer] nats = [1..] 

最初の行の角括弧のペアは、リスト用の組み込みt および新しいHaskellコンストラクターです。 2行目では、括弧を使用してリストリテラルを形成します。 明らかに、メモリ内にこのような無限のリストを配置することは不可能です。 代わりに、コンパイラは要求に応じて整数を生成する関数を作成します。 Haskell : , , . , , , . strlen , . , . , , , , ! ( ) ( ), . C++, — std::future , - , ; , , , . IO Haskell, , “Hello World!” . , , , . . , , — . , — . , — , , , , . , , , a :

 data Const ca = Const c 

Const , c a . , , , (->) .

 fmap :: (a -> b) -> Const ca -> Const cb 

, fmap , — :

 instance Functor (Const c) where fmap _ (Const v) = Const v 

C++ ( , !), , , , .

 template<class C, class A> struct Const { Const(C v) : _v(v) {} C _v; }; 

C++ - fmap , Const , .

 template<class C, class A, class B> Const<C, B> fmap(std::function<B(A)> f, Const<C, A> c) { return Const<C, B>{c._v}; } 

, Const . Δ _c , — . .

, , . , , , . , , . . , . maybeTail ( : )? , Haskell:

 maybeTail :: [a] -> Maybe [a] maybeTail [] = Nothing maybeTail (x:xs) = Just xs 

( , Nil [] . Cons : ().) maybeTail , Maybe [] , a . fmap , f : Maybe list ? . fmap , Maybe . f Maybe , f . ( fmap f ), . , Maybe list :

 square x = x * x mis :: Maybe [Int] mis = Just [1, 2, 3] mis2 = fmap (fmap square) mis 

, , fmap Maybe , , — list . , , :

 mis2 = (fmap . fmap) square mis 

, fmap :

 fmap :: (a -> b) -> (fa -> fb) 

, fmap (fmap . fmap)

 square :: Int -> Int 

 [Int] -> [Int] 

fmap

 Maybe [Int] -> Maybe [Int] 

mis . , , fmap fmap . : , ( , ). , , , . , . ? , , . . , , . , Cat ( , ). "" , , -, , . , "". , , , . , .

演習

1. `Maybe` ,
   fmap _ _ = Nothing
   ? (: )
2. `reader` (: ).
3. reader (, , Haskell).
4. . , ( ).

謝辞

. .
leshabirukov : Bodigrim , . .