こんにちは、Habr! さまざまな芸術的スタイルの写真のスタイリングのテーマが、これらのインターネット上で活発に議論されていることにお気づきでしょう。 これらの人気のある記事をすべて読むと、これらのアプリケーションの裏で魔法が起こっていると思うかもしれません。そして、ニューラルネットワークは本当にイメージを空想し、ゼロから再描画します。 偶然にも、私たちのチームが同様のタスクに直面しました。社内の企業ハッカソンの一環として、 ビデオのスタイルを作りました 写真の申請は既に存在します。 この投稿では、このネットワークがどのように画像を「再描画」するかを理解し、これを可能にした記事を分析します。 この資料を読む前に、 最後の投稿と、一般に畳み込みニューラルネットワークの基本をよく理解することをお勧めします。 いくつかの式、少しのコード( TheanoとLasagneの例を挙げます)、および多くの写真があります。 この投稿は、記事の外観、およびそれに応じてアイデア自体の発生順に作成されます。 時々、最近の経験でそれを薄めます。 ここに注目を集める地獄の少年がいます。
最初に言及する価値があるのは、著者がニューラルネットワークがブラックボックスではなく、完全に解釈可能なものであることを示すことができた記事です(ところで、今日、これはコンピュータービジョンのたたみ込みネットワークについてだけではありません )。 著者は、隠れ層ニューロンの活性化を解釈する方法を学ぶことにしました。そのため、数年前に提案されたデコンボリューションニューラルネットワーク (deconvnet)を使用しました(ちなみに、この出版物の著者である同じZeilerとFergusによって)。 デコンボリューショナルネットワークは、実際には畳み込みとプーリングを備えた同じネットワークですが、逆の順序で適用されます。 元のdeconvnetの作業では、ネットワークは教師なしモードで画像を生成するために使用されました。 今回、著者は、ネットワークを直接通過した後に得られた標識から元の画像への戻り通路にそれを単純に適用しました。 結果は、ニューロンでこの活性化を引き起こした信号として解釈できる画像です。 当然、質問が発生します:畳み込みと非線形性を通過させる方法は? さらに、最大プーリングを通じて、これは確かに可逆的な操作ではありません。 3つのコンポーネントすべてを検討してください。
逆ReLu
たたみ込みネットワークでは、 ReLu(x)= max(0、x)がアクティベーション関数としてよく使用され、レイヤー上のすべてのアクティベーションが非負になります。 したがって、非線形性を通過する場合、非負の結果を取得する必要もあります。 このため、著者は同じReLuの使用を提案しています。 Theanoアーキテクチャーの観点から、操作の勾配の関数を再定義する必要があります( 無限に価値のあるラップトップはlasagnaのレシピにあり 、そこからModifiedBackpropクラスが何であるかの詳細を学習します)。
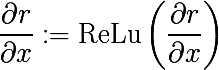
class ZeilerBackprop(ModifiedBackprop): def grad(self, inputs, out_grads): (inp,) = inputs (grd,) = out_grads
逆畳み込み
ここでは少し複雑ですが、すべてが論理的です。同じ畳み込みカーネルの転置バージョンを適用するのに十分ですが、直接パスに使用される前のレイヤーではなく、逆のReLuからの出口に適用します。 しかし、これは言葉ではそれほど明白ではないのではないかと心配しています。この手順の視覚化を見てみましょう( ここでは、畳み込みの視覚化をさらに見つけることができます)。
ストライド= 1の畳み込み| ストライド= 1の畳み込み | 逆バージョン |
|---|
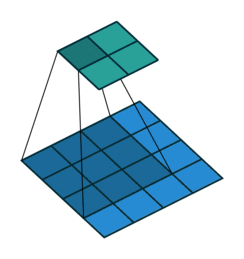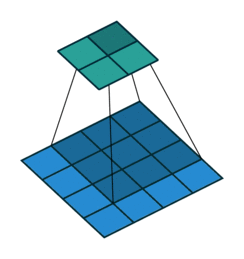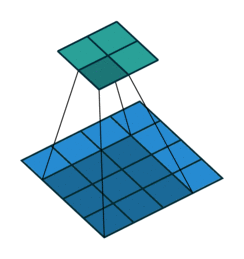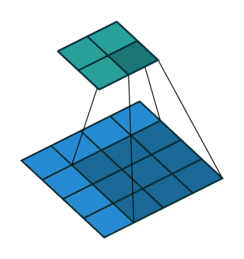 | 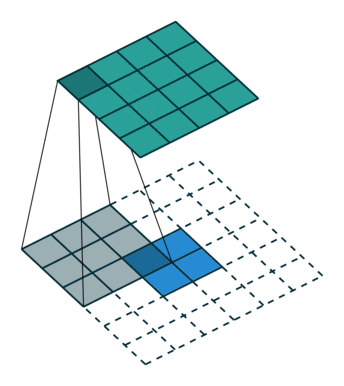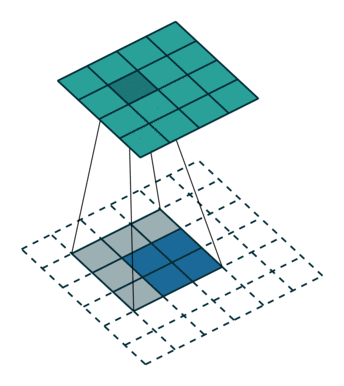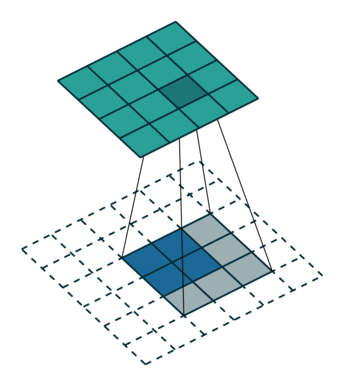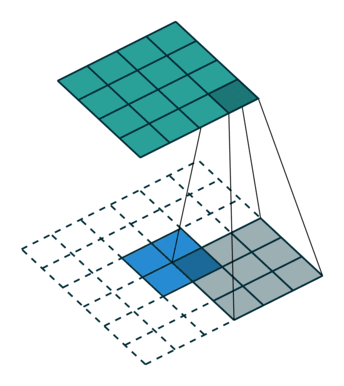 |
ストライド= 2の畳み込み| ストライド= 2の畳み込み | 逆バージョン |
|---|
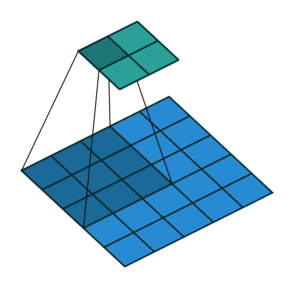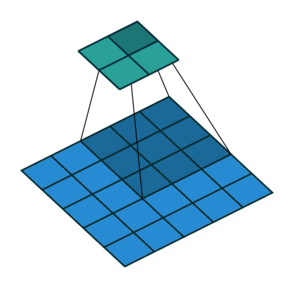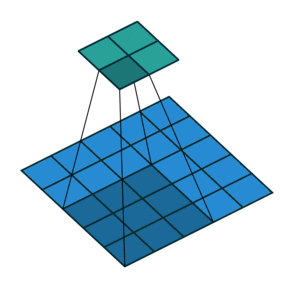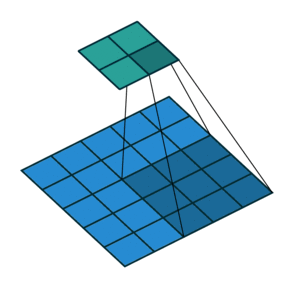 | 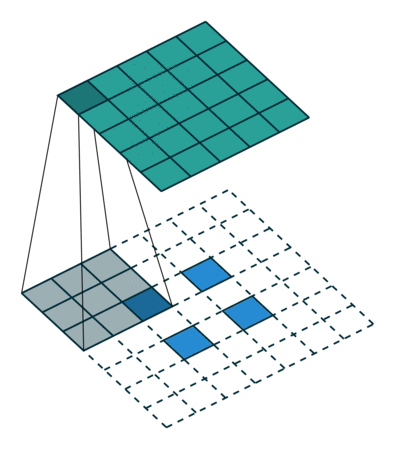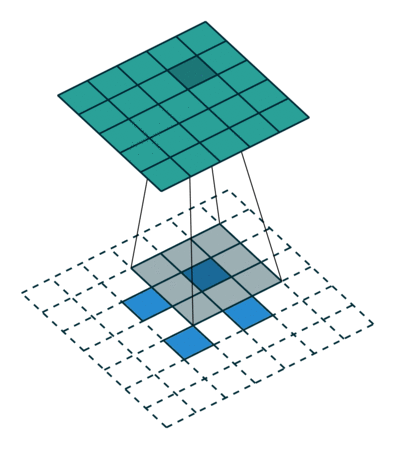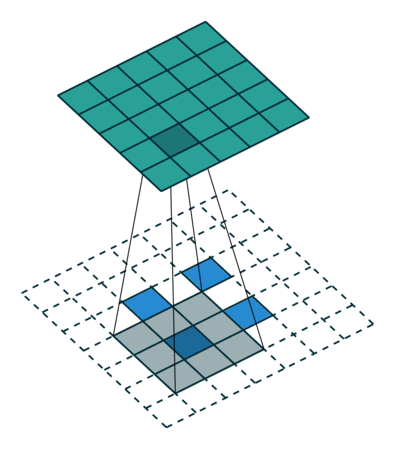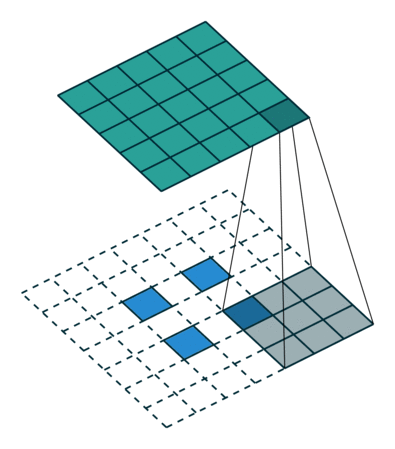 |
逆引き
この操作は(以前の操作とは異なり)一般に可逆的ではありません。 ただし、リターンパスでは何らかの方法で最大値を通過したいと考えています。 これを行うために、著者らは、ダイレクトパスで最大値が存在した場所のマップを使用することを提案しています(最大位置切り替え)。 リターンパス中、入力信号は初期信号の構造をほぼ保存するような方法でスプーフィングに変換されます;ここでは、説明するよりも実際に見やすくなっています。

結果
視覚化アルゴリズムは非常に簡単です。
- 直接パスを作成します。
- 興味のあるレイヤーを選択します。
- 1つ以上のニューロンの活性化を修正し、残りをゼロにします。
- 逆の結論を導きます。
下の画像の各灰色の四角は、フィルター(畳み込みに使用)または1つのニューロンの重みの視覚化に対応し、各カラー画像は、対応するニューロンをアクティブにする元の画像の部分です。 わかりやすくするために、1つのレイヤー内のニューロンはテーマグループにグループ化されています。 一般に、ニューラルネットワークは視覚システムの構造に関する研究でフーベルとワイゼルが書いたものを正確に学習していることが突然判明しました。これに対して、彼らは1981年にノーベル賞を受賞しました。 この記事のおかげで、畳み込みニューラルネットワークが各層で学習する内容を視覚的に表現できました。 後で生成された画像の内容を操作できるようになるのはこの知識ですが、これはまだまだ先のことであり、今後数年間はニューラルネットワークの「改pan」の方法の改善に費やされます。 さらに、この記事の著者は、より良い結果を得るために畳み込みニューラルネットワークのアーキテクチャをどのように構築するかを分析する方法を提案しました(ImageNet 2013には勝てなかったが、トップに達しましたが、 UPD :クラリファイが勝っていると判明しました)。
deconvnetを使用したアクティベーションの視覚化の例を次に示します。今日、この結果はすでにかなりまあ見えますが、それはブレークスルーでした。
この記事は、畳み込みニューラルネットワークに囲まれた知識を視覚化する方法の研究に専念します。 著者らは、勾配降下法に基づいた2つの視覚化方法を提案しています。
クラスモデルの可視化
したがって、特定の数のクラスの分類問題を解決するために訓練されたニューラルネットワークがあると想像してください。 で示す 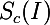 クラスcに対応する出力ニューロンの活性化値。 次に、次の最適化タスクにより、選択したクラスを最大化するイメージが正確に得られます。
クラスcに対応する出力ニューロンの活性化値。 次に、次の最適化タスクにより、選択したクラスを最大化するイメージが正確に得られます。
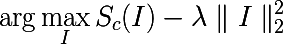
この問題は、Theanoを使用して簡単に解決できます。 通常、フレームワークにモデルパラメーターに関する導関数を取得するように依頼しますが、今回はパラメーターが固定され、導関数が入力画像から取得されると考えています。 次の関数は、出力レイヤーの最大値を選択し、入力画像の導関数を計算する関数を返します。
def compile_saliency_function(net): """ Compiles a function to compute the saliency maps and predicted classes for a given minibatch of input images. """ inp = net['input'].input_var outp = lasagne.layers.get_output(net['fc8'], deterministic=True) max_outp = T.max(outp, axis=1) saliency = theano.grad(max_outp.sum(), wrt=inp) max_class = T.argmax(outp, axis=1) return theano.function([inp], [saliency, max_class])
おそらくインターネット上で犬の顔をした奇妙な画像、DeepDreamを見たでしょう。 元の記事では、作成者は次のプロセスを使用して、選択したクラスを最大化する画像を生成します。
- 初期イメージをゼロで初期化します。
- この画像から微分値を計算します。
- 派生物から得られた画像を追加して、画像を変更します。
- 手順2に戻るか、サイクルを終了します。
次の画像が取得されます。

そして、最初の画像を実際の写真で初期化し、同じプロセスを開始するとどうなりますか? しかし、各反復でランダムクラスを選択し、残りをゼロにし、導関数の値を計算すると、そのような深い夢が得られます。
犬や目の顔がこんなに多いのはなぜですか? 簡単です:1000クラスのイメージでは、200匹近くの犬がいて、目があります。 また、人だけがいる多くのクラスもあります。
クラスの顕著性の抽出
このプロセスを実際の写真で初期化し、最初の反復後に停止し、導関数の値を描画すると、そのような画像を取得して元の画像に追加し、選択したクラスのアクティベーション値を増やします。
繰り返しますが、結果は「まあまあ」です。 これはアクティベーションを視覚化する新しい方法であることに注意することが重要です(最後のレイヤーではなく、一般的にネットワークの任意のレイヤーでアクティベーション値を修正し、入力画像の微分を取得することを妨げるものはありません)。 次の記事では、以前のアプローチの両方を組み合わせて、スタイル転送のセットアップ方法に関するツールを提供します。これについては後で説明します。
この記事は、一般的に言えば、視覚化に関するものではありませんが、プーリングを大きなストライキを伴う畳み込みに置き換えても、品質が低下することはありません。 しかし、研究の副産物として、著者は特徴を視覚化する新しい方法を提案しました。これは、モデルが学習しているものをより正確に分析するために使用されていました。 彼らの考えはこれです:導関数を取得するだけで、デコンボリューションを行うと、入力画像上でゼロよりも小さい特徴は戻りません(入力画像にReLuを使用)。 そして、これは、逆伝播された画像に負の値が現れるという事実につながります。 一方、deconvnetを使用する場合、ReLuの導関数から別のReLuが取得されます。これにより、負の値を返すことはできませんが、結果は「まあまあ」です。 しかし、これら2つの方法を組み合わせるとどうなりますか?
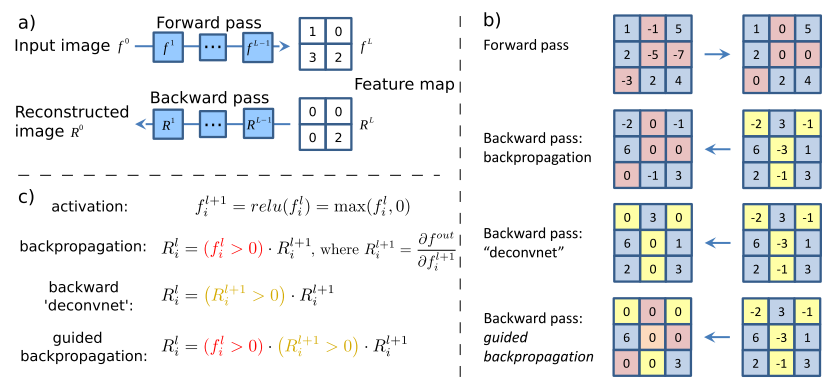
class GuidedBackprop(ModifiedBackprop): def grad(self, inputs, out_grads): (inp,) = inputs (grd,) = out_grads dtype = inp.dtype return (grd * (inp > 0).astype(dtype) * (grd > 0).astype(dtype),)
次に、完全にクリーンで解釈可能な画像を取得します。
ガイド付きバックプロパゲーションを使用した顕著性マップ もっと深く
考えてみましょう、しかしこれは私たちに何を与えますか? 各畳み込み層は、入力として3次元テンソルを受け取り、異なる次元d x w x hの 3次元テンソルも出力する関数であることを思い出してください。 d epthはレイヤー内のニューロンの数です;各ニューロンはサイズw igth x h 8の特徴マップを生成します。
VGG-19ネットワークで次の実験を試してみましょう。
- ニューラルネットワークの各レイヤーについて、サイコロをサイコロ内の活性化の合計の値でソートします
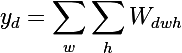 -これにより、画像内で最も顕著な兆候が得られます(同じプレートには、異なる空間座標で同じフィーチャがアクティブ化されます)。
-これにより、画像内で最も顕著な兆候が得られます(同じプレートには、異なる空間座標で同じフィーチャがアクティブ化されます)。 - 次に、各ダイで最大要素を選択します。これにより、この特徴が最も明確に表現される位置が得られます。
- そして今、1つのプレート上の1つの位置の固定値とゼロ化されたレイヤーの残りの値を持つ入力画像の微分を取ります-これは、このニューロンの受容領域(このニューロンが見ている画像の領域)だけでなく、特徴のアイデアを与えます。
conv1_2はい、ほとんど何も表示されません。 受容領域は非常に小さく、これはそれぞれ2番目の3x3畳み込み、つまり一般的な5x5領域です。 しかし、増え続けると、この機能は単なる勾配検出器であることがわかります。
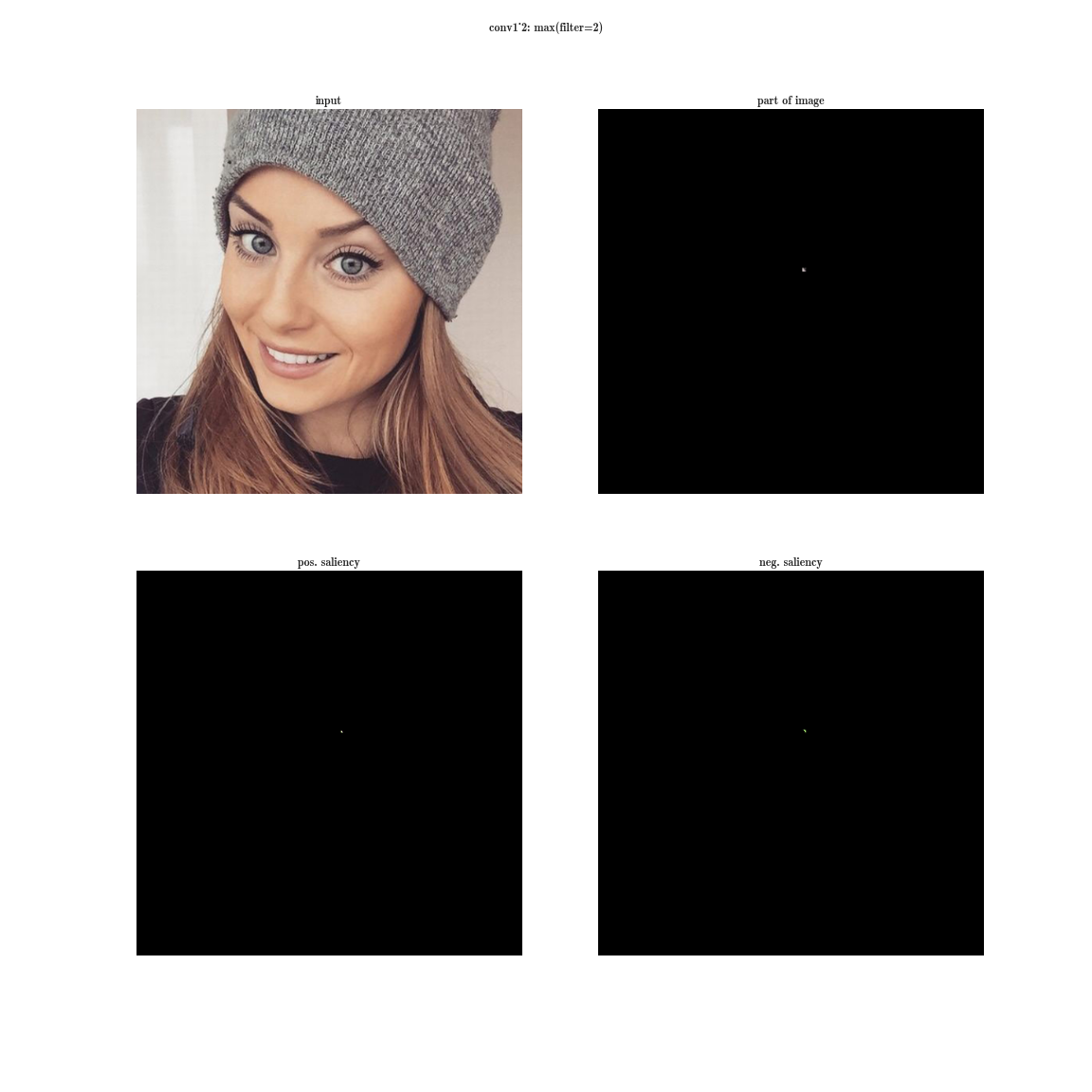
ここで、ダイの最大値ではなく、入力画像のダイのすべての要素の合計の導関数を取得することを想像してください。 その後、明らかにニューロンのグループの受容領域が入力画像全体をカバーします。 初期のレイヤーについては、明るいマップが表示されます。このマップから、これらはパターンを複雑にする方向の色検出器、グラデーション、境界などであると結論付けられます。 レイヤーが深いほど、画像は薄くなります。 これは、より深いレイヤーは検出するより複雑なパターンを持ち、複雑なパターンは単純なパターンよりも頻繁に表示されないため、アクティベーションマップはフェードします。 最初の方法は、複雑なパターンを持つレイヤーを理解するのに適しています。2番目の方法は、単純なパターンに適しています。
いくつかの画像のより完全なアクティベーションデータベースは、 こちらとこちらからダウンロードできます。
したがって、ニューラルネットワークの最初の成功した穿孔から2年が経過しました。 私たち(人間性の意味)には、ニューラルネットワークが学習していることを理解し、学習したくないものを削除できる強力なツールがあります。 この記事の著者は、1つの画像がターゲット画像に対して同様のアクティベーションマップを生成できるようにする方法を開発しています。 入力にホワイトノイズを与え、ディープドリームと同様の反復プロセスで、このイメージを、特徴マップがターゲットイメージに似ているイメージにもたらします。
コンテンツの損失
すでに述べたように、ニューラルネットワークの各層は、ある次元の3次元テンソルを生成します。
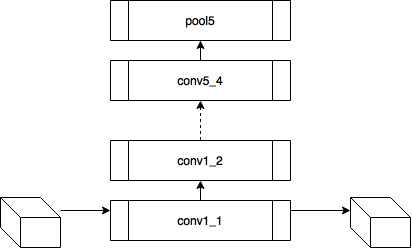
入力からのi番目の層の出力を 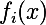 。 次に、入力画像間の残差の加重和を最小化すると
。 次に、入力画像間の残差の加重和を最小化すると 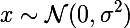 そして、 cを目指すイメージを使用して、必要なものを正確に取得します。 おそらく。
そして、 cを目指すイメージを使用して、必要なものを正確に取得します。 おそらく。
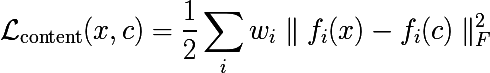
この記事の実験では、 この魔法のラップトップを使用して、GPUとCPUの両方で計算を実行できます。 GPUは、ニューラルネットワークの機能とコスト関数の値を計算するために使用されます。 Theanoは、入力画像xから目的関数eval_gradの勾配を計算できる関数を生成します。 次に、すべてがlbfgsにフィードされ、反復プロセスが開始されます。
このような関数の最適化を開始すると、ターゲットに似た画像がすぐに得られます。 これで、ホワイトノイズから一部のコンテンツ画像に類似した画像を再作成できます。
コンテンツの損失:conv4_2コンテンツ画像

最適化プロセス

結果の画像には次の2つの特徴があります。
- 色が失われます-これは、特定の例ではconv4_2レイヤーのみが使用されたという事実の結果です(言い換えれば、重みwはゼロではなく、他のレイヤーではゼロでした)。 覚えているように、色とグラデーションの遷移に関する情報を含むのは初期の層であり、後の層はより詳細な情報を含んでいます。これらは観察されます-色は失われ、内容は失われません。
- 一部の家は「行った」、つまり 直線はわずかに湾曲しています-これは、レイヤーが深いほど、含まれるフィーチャの空間位置に関する情報が少ないためです(畳み込みとプーリングの使用の結果)。
初期レイヤーを追加すると、色の状況がすぐに修正されます。
コンテンツの損失:conv1_1、conv2_1、conv4_2 この時点で、ホワイトノイズから画像に再描画されるものを制御できると思います。
スタイルロス
そして、私たちは最も興味深いことに到達しました。どのようにスタイルを伝えることができますか? スタイルとは何ですか? スタイルは、コンテンツの損失で最適化されたものではないことは明らかです。フィーチャの空間的位置に関する多くの情報が含まれているためです。 そのため、最初に行うことは、各レイヤーで取得した表現からこの情報を何らかの方法で削除することです。
著者は次の方法を提供します。 特定のレイヤーの出口でテンソルを取得し、空間座標でそれを展開し、ダイ間の共分散行列を計算します。 Gによるこの変換を示します。 私たちは本当に何をしましたか? プレート内のサインがペアで出会う頻度を計算したと言うことができます。つまり、プレート内のサインの分布を多次元正規分布で近似したと言えます。

次に、スタイル損失が次のように導入されます。ここで、 sはスタイル付きの画像です。
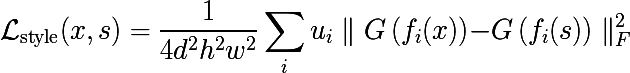
ヴィンセントに挑戦しましょうか? 原則として、ゴッホスタイルのノイズ、フィーチャの空間配置に関する情報は完全に失われます。
しかし、定型化された画像の代わりに写真を入れたらどうでしょうか? おなじみの機能、おなじみの色が得られますが、空間的な位置は完全に失われます。
どうして私たちが共分散行列を計算しているのかについて質問したのであって、他のことではないのですか? 結局のところ、空間座標が失われるように、フィーチャを集約する多くの方法があります。 これは本当に未解決の質問であり、非常に単純なものを採用しても、結果は劇的には変わりません。 これを確認しましょう。共分散行列を計算するのではなく、単に各プレートの平均値を計算します。

複合損失
当然、これら2つのコスト関数を混在させたいという要望があります。 次に、ホワイトノイズからそのような画像を生成し、コンテンツ画像(空間座標への参照を持つ)の属性を保存します。また、空間座標に付加されていない「スタイル」記号もあります。 コンテンツ画像の詳細がその場所からそのまま残ることを望みますが、正しいスタイルで再描画されます。
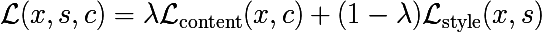
実際、正規化ツールもありますが、簡単にするために省略しています。 次の質問に答える必要があります:最適化にはどのレイヤー(重み)を使用する必要がありますか? そして、私はこの質問に対する回答がなく、記事の著者もいないことを恐れています。 彼らは以下を使用することを提案していますが、これは他の組み合わせがもっとうまく機能することを意味するものではありません。検索スペースが大きすぎます。 モデルの理解から続く唯一のルール:隣接するレイヤーを取ることは意味がありません。 それらのキャラクターは互いに大きく異なることはないので、conv * _1が各グループのレイヤーごとにスタイルに追加されます。
最終モデルは次のように表すことができます。

プロセスを制御しようとする
現在の記事の2年前に、以前の部分を思い出してみましょう。他の科学者は、ニューラルネットワークが実際に学習することを調査しました。 これらのすべての記事を活用して、さまざまなスタイル、さまざまな画像、さまざまな解像度とサイズの機能の視覚化を充実させ、どのレイヤーをどの程度の重量にするかを理解することができます。 しかし、レイヤーを再計量しても、何が起こっているかを完全に制御することはできません。 ここでの問題はより概念的なものです。 間違った関数を最適化しています ! どうして? 答えは簡単です。この関数は残差を最小限に抑えます。 しかし、私たちが本当に欲しいのは、画像が好きだということです。 コンテンツとスタイル損失関数の凸の組み合わせは、私たちの心が美しいと考えるものの尺度ではありません。 スタイリングが長すぎると、コスト関数は自然に低下しますが、結果の美的美しさは急激に低下することがわかりました。
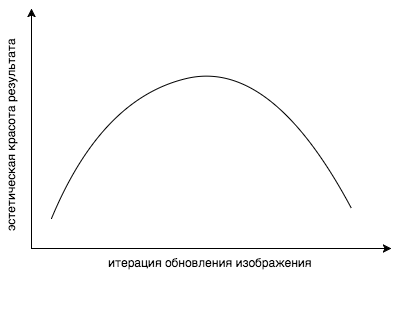
まあ、別の問題があります。 必要な機能を抽出するレイヤーを見つけたとします。 いくつかのテクスチャが三角形であるとしましょう。 しかし、このレイヤーには、たとえば円など、他の多くの機能がまだ含まれていますが、結果の画像では表示したくないのです。 一般的に、百万人の中国人を雇うことができれば、スタイル画像のすべての特徴を視覚化し、徹底的な検索によって必要なものだけをマークし、それらをコスト関数にのみ含めることができます。 しかし、明らかな理由から、これはそれほど単純ではありません。 しかし、スタイル画像の結果に表示したくないすべてのサークルを削除した場合はどうなりますか? その後、円に応答する対応するニューロンの活性化は、単に機能しません。 そして、もちろん、これは結果の画像には表示されません。 花と同じもの。 たくさんの色で鮮やかな画像を想像してください。 色の分布は空間全体で非常に不鮮明になり、結果の画像の分布は同じになりますが、最適化プロセス中に、元のピークは失われます。 カラーパレットのビット深度を単純に減らすことで、この問題を解決できることがわかりました。 ほとんどの色の分布密度はゼロに近く、いくつかの領域に大きなピークがあります。 したがって、Photoshopでオリジナルを操作することにより、画像から抽出された属性を操作します。 数学の言語で表現するよりも、視覚的に表現する方が簡単です。 またね その結果、フォトショップとサインを視覚化するスクリプトを装備したデザイナーとマネージャーは、数学者がプログラマーを使用した場合よりも3倍速い結果を達成しました。
色と特徴サイズの操作の例| オリジナル | 劣化バージョン |
|---|
 |  |
または、すぐにスタイルとしてシンプルな画像を撮ることができます そして、これはvidosikですが、適切なテクスチャーでのみです , . . , lbfgs , . , , 10-15 . . . 17 , . , , ( Style Loss ). , , , .
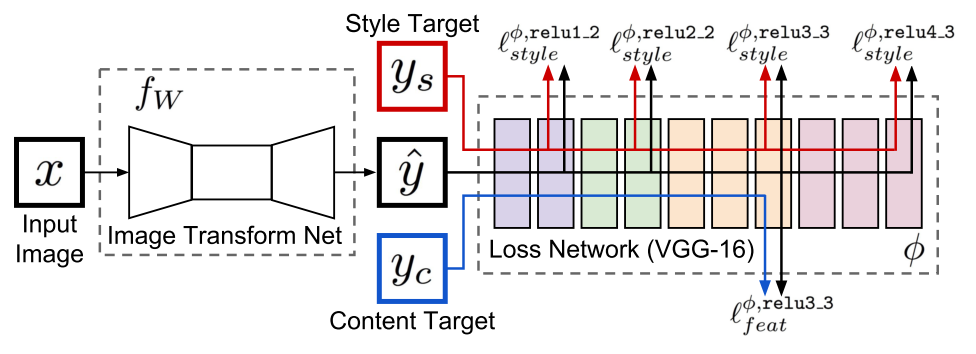
, . -. , z , . - , .. Loss- , .
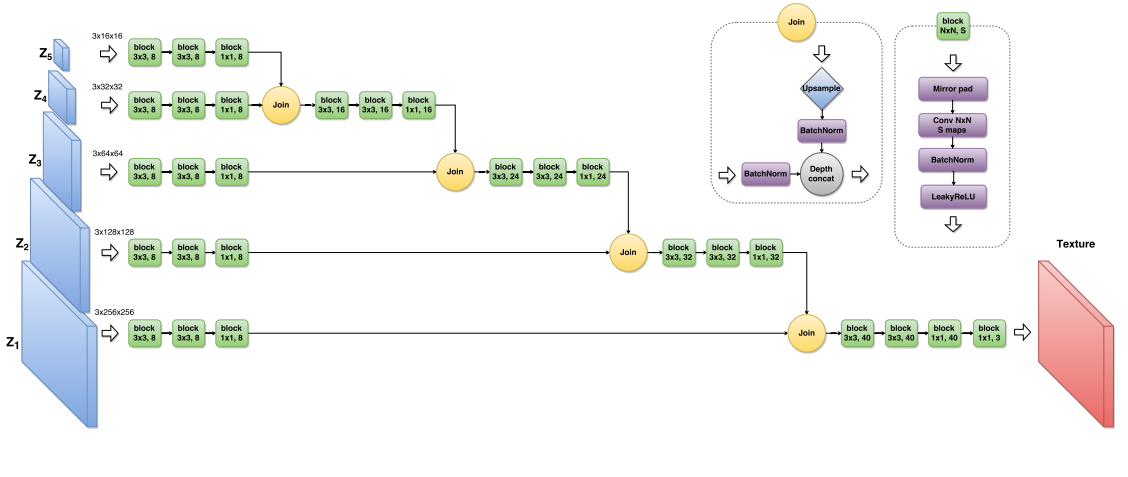
, , 17 , . residual learning .
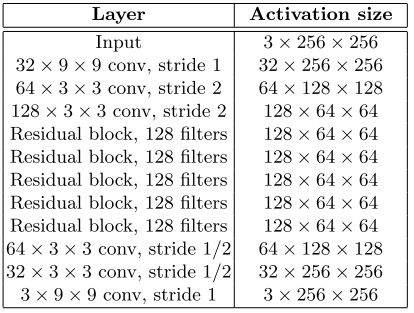
residual block conv block.
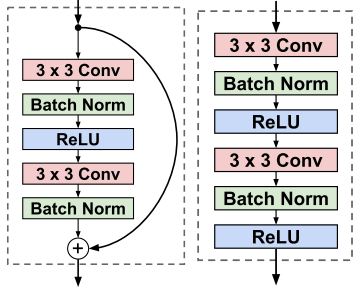
, ( ).
終了
- :
: