堅牢なコントローラーとは何ですか?なぜ私たちの生活が複雑になるのですか? 誰もが認識できる標準のPIDコントローラーに適さないものは何ですか?
答えは英語からのタイトルそのものにあります。 「堅牢性」-強くて壊れにくいという品質。 コントローラーの場合、これは、制御オブジェクトの変更に耐える「堅牢」でなければならないことを意味します。 例:マット。 DCモーターモデルには、3つの主要なパラメーターがあります。巻線の抵抗とインダクタンス、および定数で、これらは互いに等しくなります。 従来のPIDコントローラーを計算するには、データシートを見て、これらの3つのパラメーターを取得し、PID係数を計算します。すべてが簡単に思えますが、他に必要なことは何ですか。 しかし、モーターは、たとえば高周波ダイナミクスの結果として、これらの3つの係数が一定ではない実際のシステムであり、記述が困難であるか、システムの高次数が必要です。
たとえば、 Rdatashit = 1 Ohmですが、実際には、Rは[0.9,1.1] Ohmの範囲にあります。 したがって、PIDコントローラーの品質インジケーターの場合、設定されたものを超えることができ、堅牢なコントローラーは不確実性を考慮し、閉じたシステムの品質インジケーターを適切な間隔に保つことができます。
この段階で、論理的な疑問が生じ
ます。この間隔を見つける方法は? モデルのパラメトリック識別を使用して検出されます。 Habréは最近、OLSの方法(
「線形動的システムのパラメーター同定
」 )について説明しましたが、データシートのように、同定可能なパラメーターの1つの値を与えます。 値の範囲を見つけるために、
MATLABのスパースセミド有限プログラミングの多項式最適化問題の緩和の補足を使用しました。 興味深い場合は、このパッケージの使用方法と識別方法を別の記事に書くことができます。
堅牢な制御が必要な理由が今では少なくともそれほど明確ではないことを願っています。
理論については特に理解しませんでした。 コントローラを取得するために必要な手順を示します。 興味のある人は、Essentials Of Robust Control、Kemin Zhou、John C. Doyle、Prentice Hall、またはMatlabのドキュメントを読むことができます。
次の制御システム図を使用します。
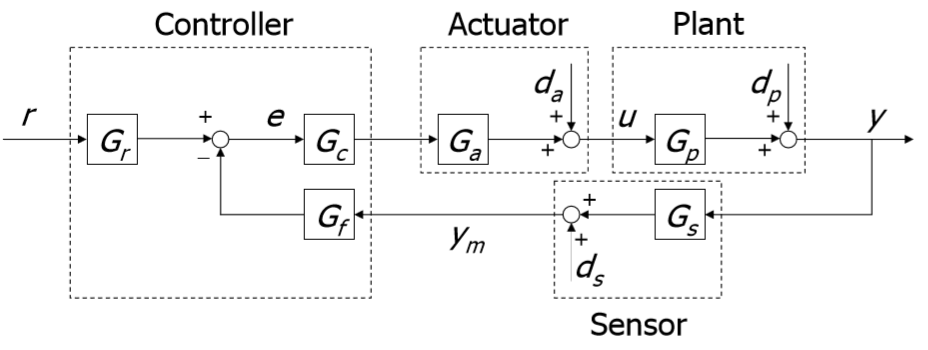 図1 :制御システムのブロック図
図1 :制御システムのブロック図私はここですべてが明確であると思います(ディ-妨害)。
問題文:Find :指定されたすべての条件を満たすGc(s)およびGf(s)。
与えられた :
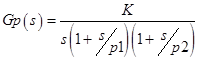
-間隔によって与えられる不確実性を持つ制御オブジェクト:
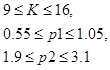
さらに計算するために、名目値を使用し、不確実性をさらに考慮します。
Kn =(16 + 9)/2=12.5,p1n=0.8,p2n=2.5それぞれ、公称制御オブジェクトを受け取りました:
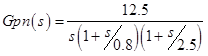
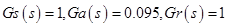
妨害の種類:
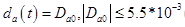 -振幅D_a0の増幅器の段階的外乱
-振幅D_a0の増幅器の段階的外乱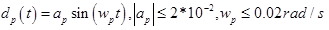 -振幅a_pおよび周波数w_pの制御オブジェクトの正弦波妨害
-振幅a_pおよび周波数w_pの制御オブジェクトの正弦波妨害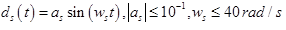 -振幅a_sおよび周波数w_sのセンサーの正弦波妨害
-振幅a_sおよび周波数w_sのセンサーの正弦波妨害
言い換えれば、これらはシステム要素のノイズ特性です。
性能仕様- 制御システムのゲインKd = 1
- 入力インパクト時の定常状態エラーランプR0 = 1:
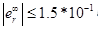
- daの存在下で確立されたエラー:
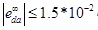
- dpが存在する場合の定常エラー:
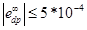
- dsが存在する場合の定常エラー:
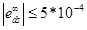
- オーバーシュート
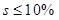
- 規制時間
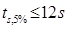
- 立ち上がり時間
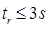
解決策
主なポイントのみを詳しく説明します。
H∞メソッドの重要なステップの1つは、入力および出力の重み関数の定義です。 これらの重み付け関数は、入力および出力を正規化し、入力外乱の時間および周波数依存性と出力変数の動作特性(誤差)を反映するために使用されます[1]。 正直なところ、これは実際には私には何の意味もありません。特にこの方法に初めて触れる場合は。 簡単に言えば、制御システムの目的のプロパティを設定するために、重み関数が使用されます。 たとえば、フィードバックには、通常は高周波数のノイズがあるセンサーがあるため、重み関数は、コントローラーがセンサーノイズを除去するために交差してはならない一種の境界になります。
以下では、パフォーマンスに基づいてこれらの重み関数を導き出します。
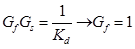 ここではすべてが簡単です。
ここではすべてが簡単です。- この段落では、条件2を満たすためにコントローラー(μを表す)が必要なゼロの極数を決定する必要があります。これを行うには、次の表を使用します。
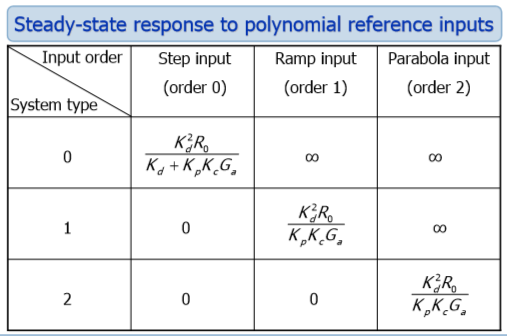
図2 :位置、速度、加速度のエラー
システムタイプまたは非統計(p)-制御オブジェクトであるゼロの極の数を示します。この例では、p = 1(1次の非統計を持つシステム)です。 制御オブジェクトは1次の統計量を持つシステムであるため、この場合、コントローラーの極はゼロにしないでください。 次の式を使用します。
μ+ p = h
ここで、hは入力信号の次数で、ランプh = 1の場合。
μ= hp = 1-1 = 0
ここで、有限値定理を使用してe_r∞を見つけます
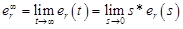
e_rは追跡エラーです。
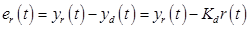
yrは実際の出力(図1を参照)、ydは目的の出力
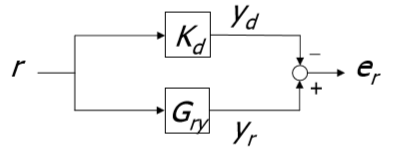
図3 :トラッキングエラー検出
その結果、次のようになります。
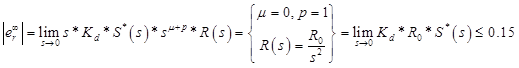
これは、この方程式S(感度関数)で不明な定常状態の誤差式です。
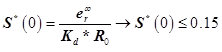
どこで 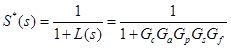 -感度関数、L(s)-ループ関数。 それらがどのようにロシア語に翻訳されるかについての手掛かりがなければ、私は英語名のままにします。 相補感度関数
-感度関数、L(s)-ループ関数。 それらがどのようにロシア語に翻訳されるかについての手掛かりがなければ、私は英語名のままにします。 相補感度関数 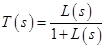 (式からわかるように、SとTにはGcが含まれます-それぞれ計算されたコントローラー、エラーとパフォーマンス特性からSとTの境界を見つけ、SとTから重み関数を決定し、重み関数からmatlabが目的のコントローラーを見つけます)
(式からわかるように、SとTにはGcが含まれます-それぞれ計算されたコントローラー、エラーとパフォーマンス特性からSとTの境界を見つけ、SとTから重み関数を決定し、重み関数からmatlabが目的のコントローラーを見つけます)
SとTについて簡単に説明します[1]。
- 感度関数 S(s)は、出力y(s)を外乱daとdpの関数として記述し、トラッキングエラーと入力アクション(低周波数の場合)にも関連します。
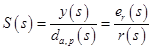
- 相補感度関数 T(s)は、システム出力と入力アクションを接続し、センサーノイズdsがシステム出力にどの程度影響するかを示します(高周波の場合)。
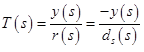
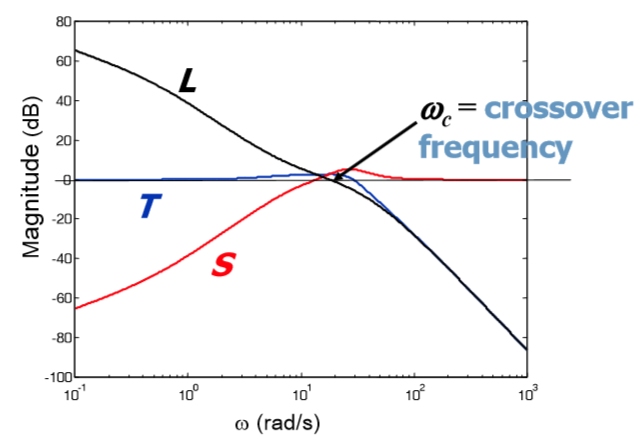
図4 :S、T、Lのボード線図
グラフは、Sが低周波外乱を減衰させ、Tが高周波外乱を減衰させることを示しています。
- e_daには有限値定理を使用します
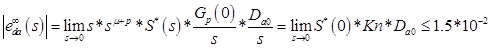
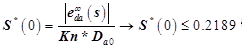
2つの不等式を取得したため、両方を満たす条件を見つけます。
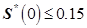
この条件は、感度関数がボード線図の0 dB軸と交差する場所を示します。
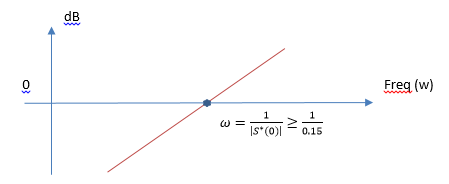
図5 :Sのボード
- Dp、低周波の高調波妨害があります。 周波数領域wpでSのマスクを作成します
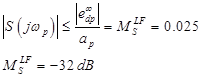
この値は、周波数wpが外乱を除去するためにSが-32 dB未満でなければならないことを示します
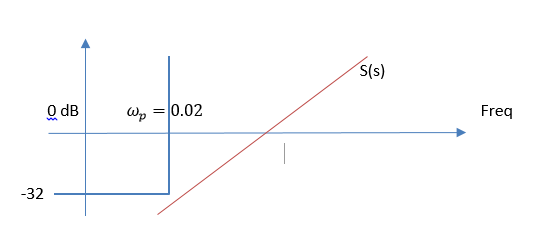
図6 :Sのマスク
- Dsは高周波の高調波妨害でもあり、ここでTはその役割を果たす
同じことをしましょう:
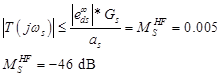
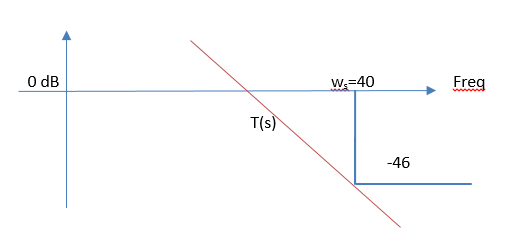
図7 :Tのマスク
重み関数の複雑な順序は、マスク条件と0軸との交差の頻度から決定されます。 この場合、wpからwまでは約10年であり、-32 dBであるため、Sは少なくとも2桁でなければなりません。 Tについても同じことが言えます。
その結果、SとTの制約はそれぞれ次のようになります。
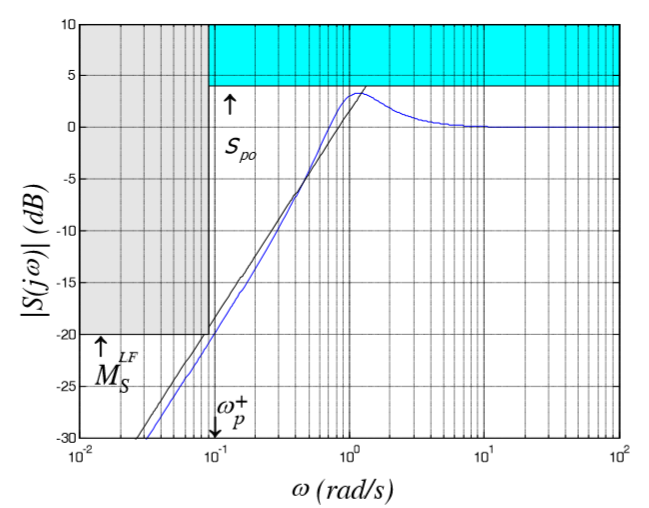
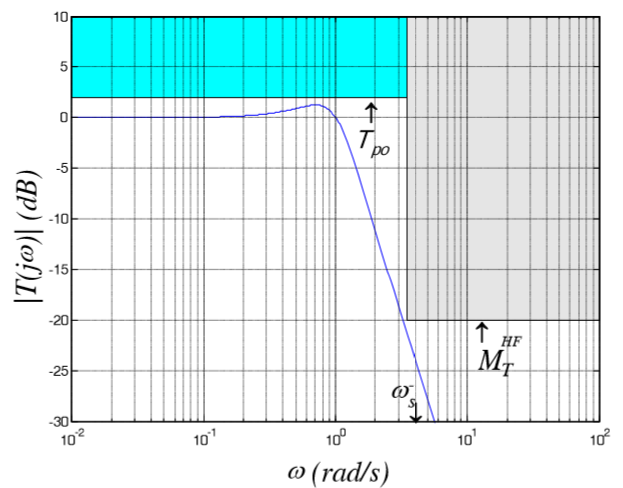
図8 :SおよびTのすべてのマスク
- 時間特性を変換するには、チャートを使用します
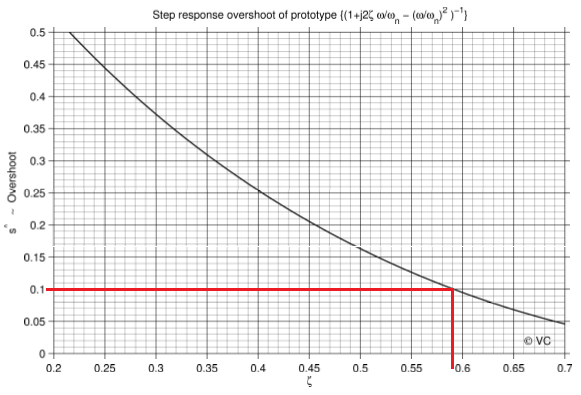
図9 :減衰係数と再調整
再調整を知って、10%の減衰係数を見つけます->
ξ= 0.59
減衰係数がわかると、SおよびTの(共振)最大許容値がわかります
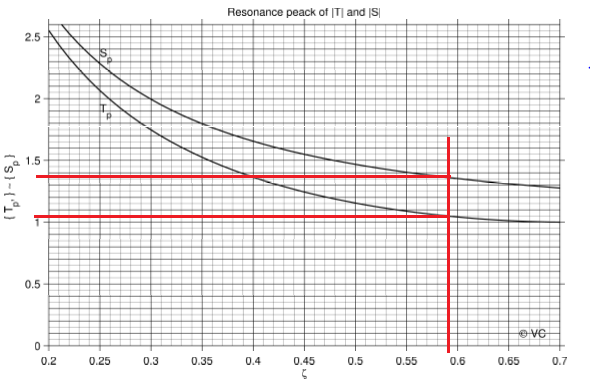
図10 :S_p0およびT_p0と減衰係数のグラフ
S_p0 = 1.35
T_p0 = 1.05
- 規制と調整の時から、制御システムがどれくらい速くあるべきかを見つけます

次に、Sの固有振動数を求めます
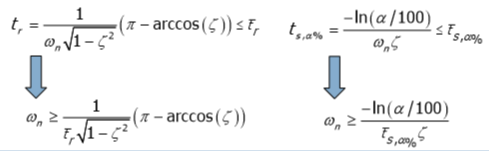
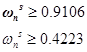
Tの固有振動数は、ボード線図から求められます。 条件5によると、40 rad / sの周波数では、Tは-46 dB未満である必要があります。つまり、-40 dB / decの勾配では、固有周波数は4 rad / s未満でなければなりません。 ボードを作成するには、最適な値を選択します。
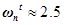
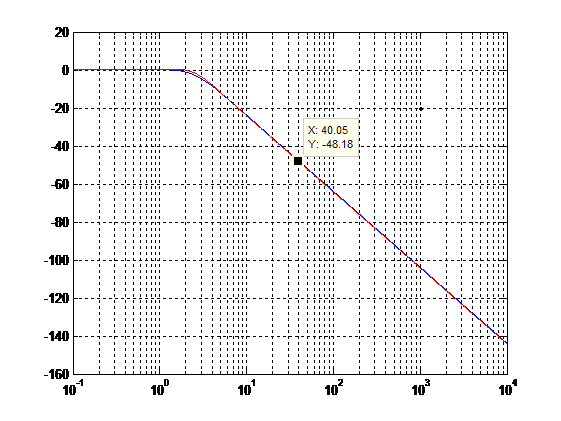
図11 :ボードT関数
その後、STを構築するためのすべてのデータを取得し、それを重み関数に変換します。 STの形式は次のとおりです。
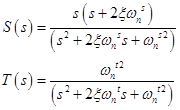
通常、バターワース係数は重み関数の構築に使用されます。
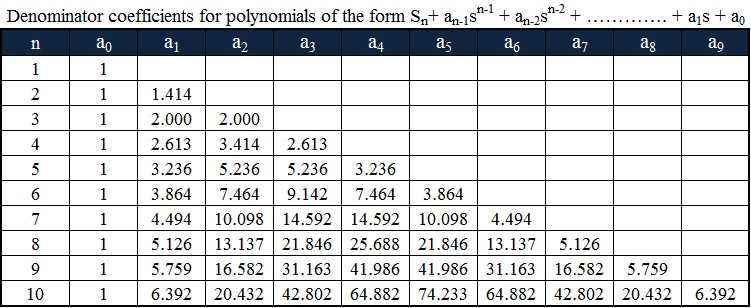
重み関数の形式は次のとおりです。
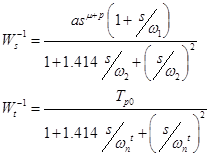
のために 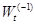 すべてが単純であり、式に代入する必要があるすべてのものがあります。 のために
すべてが単純であり、式に代入する必要があるすべてのものがあります。 のために 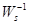 さらに計算が必要です。
さらに計算が必要です。
パフォーマンス特性は、コントローラがすべての条件を満たす境界条件を提供するためです。 重み付け関数は、すべての条件を組み合わせて、すべての条件を満たすコントローラーが配置される左右の境界として使用されます。
のために 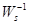
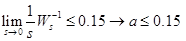 このパラメーターは一般化DCゲインと呼ばれ、低周波数(s = 0)の動作を表示します
このパラメーターは一般化DCゲインと呼ばれ、低周波数(s = 0)の動作を表示します
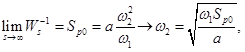 、w1、おおよそ摂動周波数の近くまたは1ディケード以下を選択します(0.0005 rad / sに設定)
、w1、おおよそ摂動周波数の近くまたは1ディケード以下を選択します(0.0005 rad / sに設定)
- •LMIソルバーは、関数のゼロ(原点ではゼロ)を認識しないため、原点付近でsをゼロに置き換えます(s + 0.0005)
その結果、以下が得られます。
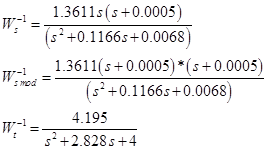
一般化された植物
Hinf法または無限ノルムHinfinityを最小化する方法は、制御問題の一般的な定式化を指し、次のフィードバック制御システム表現スキームに基づいています。
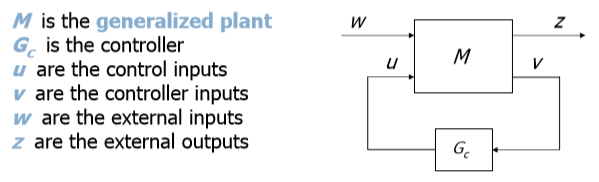 図12 :一般化された制御システム図
図12 :一般化された制御システム図コントローラーの計算と、これに必要なものに進みます。 彼らは私たちに計算アルゴリズムの研究を説明しなかった、彼らは言った:「これを行うとすべてが判明するだろう」が、原理は非常に論理的です。 コントローラーは、最適化の問題を解決する過程で取得されます。
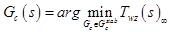
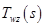
-WからZへの伝達関数を閉じた。
次に、一般化された植物を作成する必要があります(下の破線の長方形の写真)。 すでに特定したGpn。これは名目上の制御オブジェクトです。 Gc-最終的に取得するコントローラー。 W1 = Ws(s)、W2 = max(WT(s)、Wu(s))は、前に定義した重み関数です。 Wu(s)は不確実性の重み関数であり、定義しましょう。
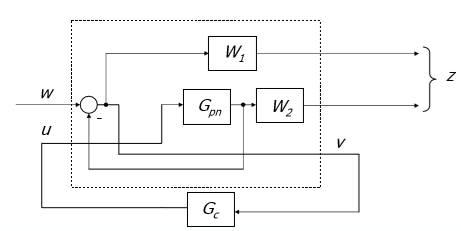 図13 :開示された制御スキーム
図13 :開示された制御スキームウー(s)
コントロールオブジェクトに乗法的不確実性があると仮定すると、これを描くことができます:
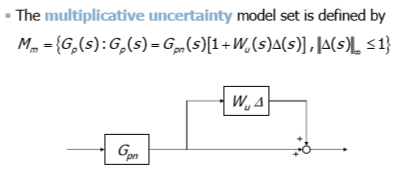 図14 :乗法的不確実性
図14 :乗法的不確実性そして、matlabを使用してWuを見つけます。 公称制御オブジェクトからの可能なすべての偏差をボードで作成し、これらの不確実性をすべて記述する伝達関数を作成する必要があります。
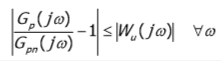
各パラメーターに対して約4つのパスを作成し、ボードを作成しましょう。 その結果、次のようになります。
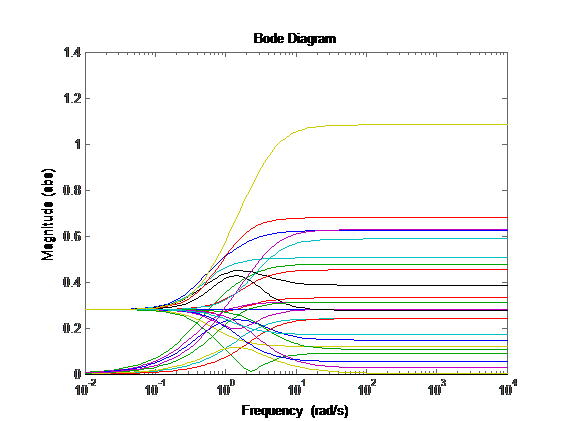 図15 :不確実性のボード線図
図15 :不確実性のボード線図ウーはこれらの線の上に横たわります。 matlabには、マウスを使用してポイントを示し、これらのポイントから伝達関数を作成できるツールがあります。
コードmf = ginput(20);
magg = vpck(mf(:、2)、mf(:、1));
Wa = fitmag(magg);
[A、B、C、D] = unpck(Wa);
[Z、P、K] = ss2zp(A、B、C、D);
Wu = zpk(Z、P、K)
点の導入後、曲線は経年変化し、伝達関数の次数を導入することが提案されています。次数2を導入します。
起こったことは次のとおりです。
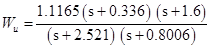
次に、W2を定義します。これのために、WtとWuを作成します。
グラフは、WtがWuよりも大きいことを示しており、W2 = Wtを意味します。
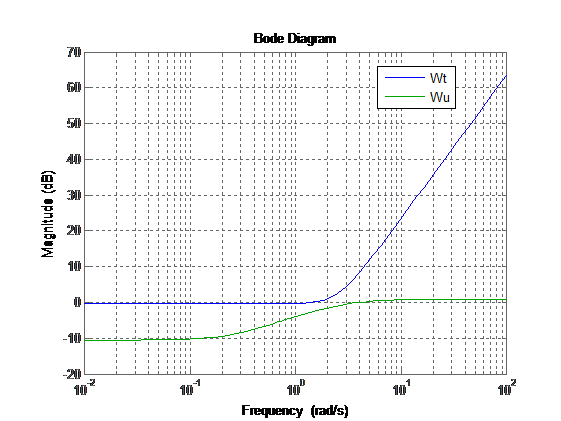 図16 :定義W2
図16 :定義W2次に、次のようにsimulinkで一般化されたプラントを構築する必要があります。
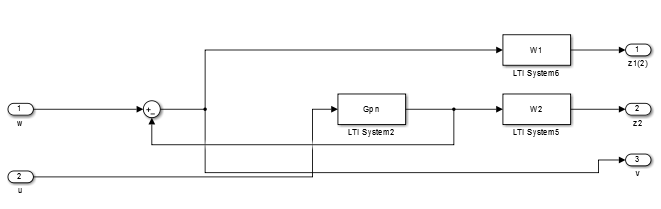 図17 :Simulinkの一般化されたプラントブロック図
図17 :Simulinkの一般化されたプラントブロック図そして、g_plant.mdlなどの名前で保存します
重要なポイント: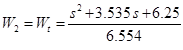
-適切なtfではなく、そのままにしておくとエラーが発生します。 したがって、
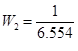
次に、「sderiv」を使用してz2出力に2つのゼロを追加します。
Matabでの実装pは2です。 T関数の頻度の領域におけるゼロの頻度
[Am、Bm、Cm、Dm] = linmod( 'g_plant');
M = ltisys(Am、Bm、Cm、Dm);
M = sderiv(M、2、[1 / p 1]);
M = sderiv(M、2、[1 / p 1]);
[gopt、Gcmod] = hinflmi(M、[1 1]、0,0.01、[0,0,0]);
[Ac、Bc、Cc、Dc] = ltiss(Gcmod);
[Gc_z、Gc_p、Gc_k] = ss2zp(Ac、Bc、Cc、Dc);
Gc_op = zpk(Gc_z、Gc_p、Gc_k)
このコードを実行した後、コントローラーを取得します。
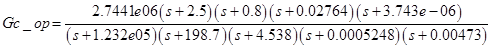
原則として、そのままにしておくことができますが、通常は低周波および高周波のゼロと極は削除されます。 したがって、コントローラーの順序を減らします。 そして、次のコントローラーを取得します。
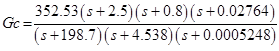
このヒコルスチャートを取得します。
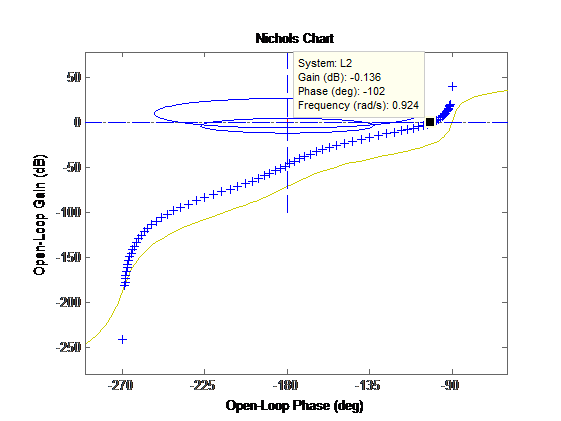 図18 :受信コントローラーを含むヒコルス線図の開ループ
図18 :受信コントローラーを含むヒコルス線図の開ループそしてステップ応答:
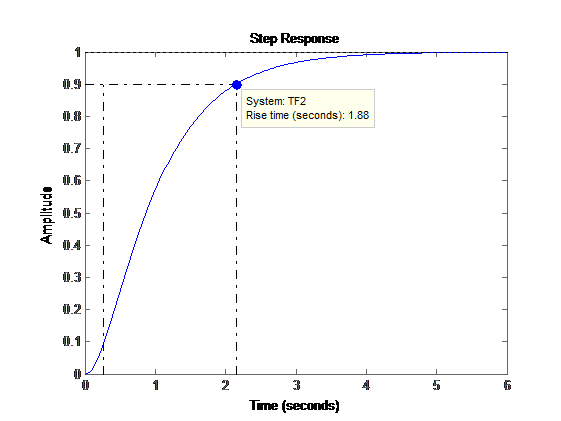 図19 :コントローラーを備えた閉ループシステムの過渡応答
図19 :コントローラーを備えた閉ループシステムの過渡応答そして今、最も甘いもの。 コントローラーが堅牢であるかどうか。 この実験では、制御オブジェクト(係数k、p1、p2)を変更し、ステップ応答と目的の特性を確認するだけです。この場合、オーバーシュート、5%の調整時間、および立ち上がり時間です[2]。

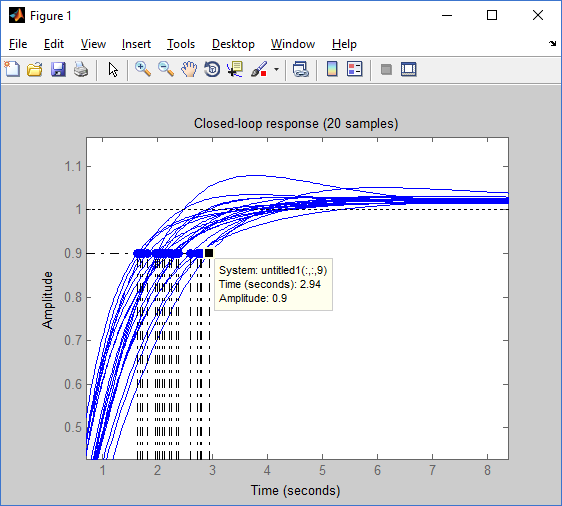
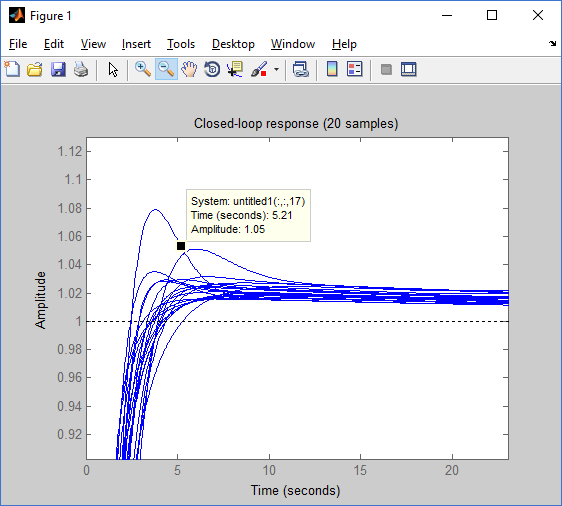 図20 :制御オブジェクトのさまざまなパラメーターの時間特性
図20 :制御オブジェクトのさまざまなパラメーターの時間特性20種類の過渡特性を構築したので、各時間特性の最大値を特定しました。
•最大再調整-7.89%
•最大立ち上がり時間-2.94秒
•最大回復時間5%-5.21秒
そして、目を見張る、名目上のオブジェクトだけでなく、パラメータ間隔にも必要な特性。
それでは、従来のPIDコントローラーと比較して、ゲームがろうそくに値するかどうかを見てみましょう。
公称制御オブジェクトのPID計算されたpidtool(上記を参照):
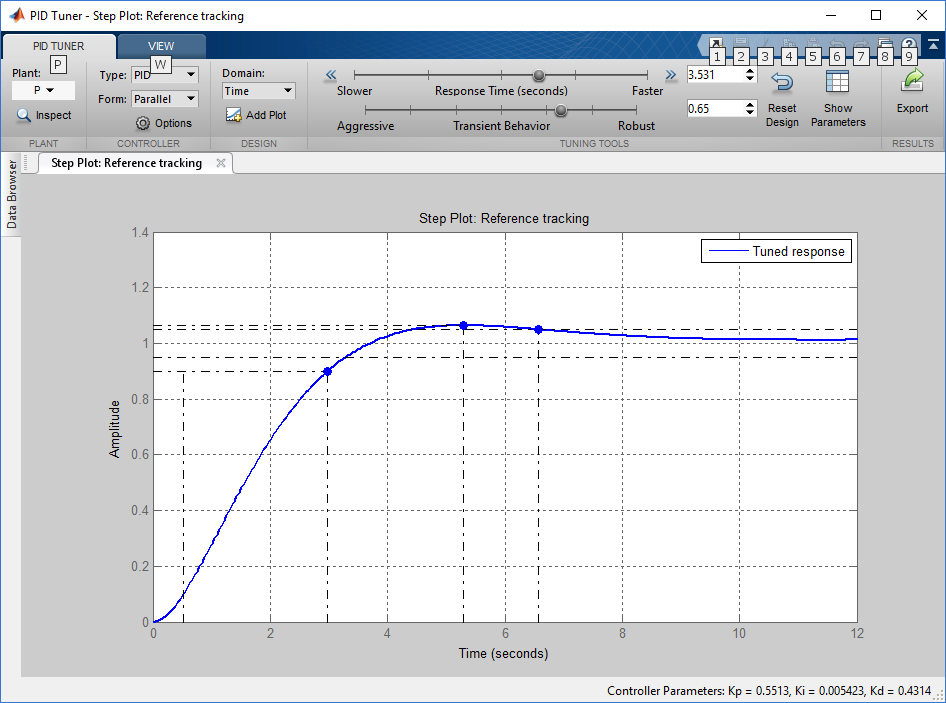 図21 :Pidtool
図21 :Pidtool次のコントローラーを取得します。
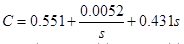
今、
H-無限対PID :
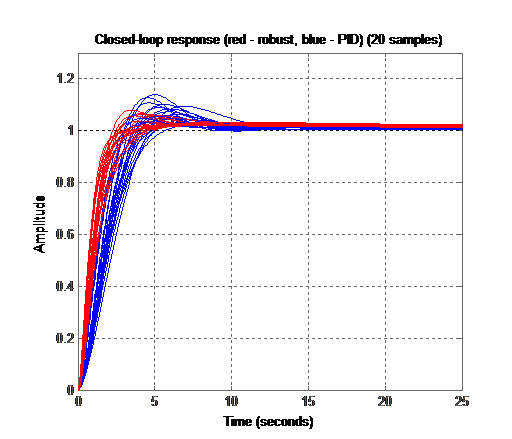 図22 :H-∞とPID
図22 :H-∞とPIDPIDはこのような不確実性に対処せず、PXは所定の制限を超え、堅牢なコントローラーはシステムをオーバーシュート、立ち上がり時間、およびレギュレーションの所定の間隔に「厳密に」維持していることがわかります。
記事を長くせず、読者を飽きさせないために、特性2-5(エラー)の検証を省略します。堅牢なコントローラーの場合、すべてのエラーは設定されたものを下回り、オブジェクトの他のパラメーターでもテストが行われました。
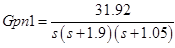
エラーはセット以下でした。つまり、このコントローラーはタスクを完全に処理します。 PIDはパラグラフ4(エラーdp)だけに対処できませんでした。
コントローラの計算はこれですべてです。 批判し、尋ねてください。
Matlabファイルリンク:
drive.google.com/open?id=0B2bwDQSqccAZTWFhN3kxcy1SY0E参照資料
1. H-Infinity Controlの重み付け関数の選択に関するガイドライン
2.
it.mathworks.com/help/robust/examples/robustness-of-servo-controller-for-dc-motor.html