すべての良い一日。 この記事では、動的システムの数学モデルを構築するためのグラフィカルな方法の1つを示します。これは、 ボンドグラフ （「ボンド」-通信、「グラフ」-グラフ）と呼ばれます。 ロシアの文学、この方法の説明では、私はトムスク工科大学、A.V。 ボロニン「メカトロニックシステムのモデリング」2008。第2種ラグランジュ方程式による古典的な方法も示します。

ラグランジュ法

理論を描くのではなく、いくつかのコメントを付けて計算の段階を示します。 個人的には、理論を10回読むよりも、例から学ぶ方が簡単です。 ロシア文学では、この方法の説明、そして実際には数学または物理学は複雑な数式で非常に飽和しているように思われ、それには深刻な数学的背景が必要です。 ラグランジュ法（イタリアのトリノ工科大学で研究している）を研究している間、ロシアの文学を研究して計算方法を比較しましたが、この方法の解決の進捗を追うのは困難でした。 ハリコフ航空研究所でのモデリングコースを思い出しても、そのような方法の結論は非常に面倒で、誰もこの問題を理解しようとはしませんでした。 これは、ラグランジュに従って数学モデルを構築するためのトレーニングマニュアルを書くことを決めたものです。まったく難しいことではないので、時間微分と偏微分を数える方法を知っていれば十分です。 より複雑なモデルの場合、回転行列が追加されますが、複雑なものもありません。

モデリング手法の特徴：

• ニュートンオイラー ： 力とモーメントの動的バランスに基づくベクトル方程式
• ラグランジュ ：運動エネルギーとポテンシャルエネルギー（エネルギー）に関連付けられた状態関数に基づくスカラー方程式
• ボンドグラフ ：システムの要素間の力の流れに基づく方法

簡単な例から始めましょう。 スプリングとダンパーを備えた重量。 重力を無視します。


図1 。 スプリングとダンパーを備えた重量

まず、次のものを示します。

• 初期座標系 （NSC）またはモーションレスck R0（i0、j0、k0） どこ？ 空に指を突くことができますが、脳内のニューロンの先端をひきつらせて、NSCをM1体の動線上に置くという考えは通ります。
• 質量を持つ各体の座標系 （M1 R1（i1、j1、k1）があります ）、向きは任意ですが、なぜ私たちの生活が複雑になるのか、NSCとの差を最小限に抑えます
• 一般化された座標 q_i （動きを記述できる変数の最小数）、この例では、1つの一般化された座標、j軸に沿った動きのみ

図2 。 座標系と一般座標を書き留めます

次に、すべてのボディの位置と速度を見つけます。 この例では、1つのボディM1：

図3 。 体の位置と速度M1

式に従って、ダンパーの運動エネルギー（C）とポテンシャル（P）のエネルギー、および散逸関数（D）を見つけました。

図4 。 完全な運動エネルギーの式

この例では、回転はありません。2番目のコンポーネントは0です。



図5 。 運動、ポテンシャルエネルギー、散逸関数の計算

ラグランジュ方程式の形式は次のとおりです。

図6 。 ラグランジュ方程式とラグランジアン

デルタW_iは、加えられた力とモーメントによって実行される仮想作業です。 彼女を見つける：

図7 。 仮想作業計算

ここで、 デルタq_1は仮想移動です。

ラグランジュ方程式のすべてを代入します。

図8 。 結果として生じるバネとダンパーを含む質量モデル

これにより、ラグランジュ法が終了しました。 ご覧のとおり、それほど難しくはありませんが、これは非常に単純な例であり、ニュートンオイラー法はおそらくもっと簡単です。 複数の物体が互いに異なる角度で回転するより複雑なシステムの場合、ラグランジュ法の方が簡単です。

ボンドグラフ法

すぐに、質量スプリングとダンパーを使用した例のモデルがボンドグラフでどのように見えるかを示します。

図9 。 バネとダンパーを備えたボンドグラフ質量

ここで、簡単なモデルを構築するのに十分な、少しの理論を話さなければなりません。 興味がある人は、本（ [Wolfgang Borutzky] Bond Graph Methodology ）または（ Voronin A.V. Modeling of mechatronic systems：a training manual。 -Tomsk：Publishing House of Tomsk Polytechnic University、2008 ）を読むことができます。

まず、複雑なシステムが複数のドメインで構成されることを定義します。 たとえば、電気モーターは、電気部品と機械部品またはドメインで構成されます。

結合グラフは 、これらのドメイン、サブシステム間の電力交換に基づいています。 任意の形式の力の交換は、常に2つの変数（ 力変数 ）によって決定されることに注意してください。これにより、動的システムの一部としてさまざまなサブシステムの相互作用を調べることができます（表を参照）。



表からわかるように、べき乗の表現はどこでもほとんど同じです。 一般に、 Powerは「 flow-f 」と「 effort-e 」の積です。

電気領域での力 （eng。Effort）は、電圧（e）、機械的力-力（F）またはモーメント（T）、油圧-圧力（p）です。

電気領域の流れ （eng。Flow）は、電流（i）、機械-速度（v）または角速度（omega）、油圧-流れまたは流体の流れ（Q）です。

これらの表記法を使用すると、パワーの表現が得られます。


図10 。 累乗変数による累乗式

ボンドグラフ言語では、電力を交換する2つのサブシステム間の接続は、コミュニケーション（eng。Bond）で表されます。 このため、この方法は、 結合グラフであるbond-graphまたはr -graph bondと呼ばれます 。 電気モーターを使用したモデルの接続のブロック図を考えます （これはボンドグラフではありません）：

図11 。 クロスドメインフロー図

電圧源がある場合、それは電圧を生成し、巻き戻しのためにエンジンに与えます（この矢印はモーターに向けられます）、巻線の抵抗に応じて、オームの法則に従って電流が現れます（エンジンから電源に向けられます）。 したがって、1つの変数はサブシステムへの入り口であり、2番目の変数はサブシステムからの出口でなければなりません。 ここで、電圧（ 努力 ）は入力であり、電流（ 流れ ）は出力です。

現在のソースを使用する場合、ダイアグラムはどのように変化しますか？ そうだね。 電流はモーターに向けられ、電圧は電源に向けられます。 その場合、電流（ フロー ）が入力、電圧（ エフォート ）が出力になります。

力学の例を考えてみましょう。 質量に作用する力。

図12 。 質量に適用される力

ブロック図は次のとおりです。

図13 。 ブロック図

この例では、Forceは質量の入力変数です。 （力は質量に適用されます）
ニュートンの第二法則によると：

質量は迅速に応答します：


この例では、1つの変数（ force - effort ）が機械領域への入り口である場合、他のpower変数（ speed - flow ）が自動的に出力になります 。

入口の位置と出口の位置を区別するために、要素間の矢印（接続）の終端で垂直線が使用されます。この線は、因果性または因果性の 記号と呼ばれます。 つまり、加えられた力が原因であり、速度が結果です。 因果関係は2つのサブシステムの物理的挙動と電力交換の結果であるため、この兆候はシステムモデルの正しい構築にとって非常に重要です。したがって、因果関係記号の場所の選択は任意ではありません。

図14 。 原因の指定

この縦線は、どのサブシステムがエフォート（ effort ）を受け取り、その結果フロー（ flow ）を生成するかを示しています。 質量の例では、次のようになります。

図14 。 質量に作用する力の因果関係

矢印から、質量の入力が力であり、出力が速度であることが明らかです。 これは、矢印が乱雑にならず、モデルの構築を体系化するために行われます。

次の重要なポイント。 一般化された運動量 （運動量）と変位 （ エネルギー変数 ）。


上記の表は、ボンドグラフ法で使用される2つの追加の物理量を紹介しています。 それらは一般化された運動量 （ p ）および一般化された変位 （ q ）またはエネルギー変数と呼ばれ、時間の経過とともに電力変数を積分することで取得できます。

図15 電力変数とエネルギー変数の関係

電気ドメインで ：

ファラデーの法則に基づいて、導体の両端の電圧は、この導体を通る磁束の導関数に等しくなります。

電流強度は、一定時間tの間導体の断面を通過した電荷量Qとこの期間の値の比に等しい物理量です。

機械的ドメイン：

ニュートンの2つの法則のうち、 強度はインパルスの時間微分です

したがって、 速度は変位の時間微分です。

要約 ：

基本的な要素

動的システムのすべての要素は、バイポーラコンポーネントと4ポールコンポーネントに分けることができます。
バイポーラコンポーネントを検討してください：

ソース
ソースには努力とフローの両方があります。 電気領域の類推： 力の源は 電圧 源であり、流れの 源は電流源です。 発生源の原因となる兆候はそのようなもののみであるべきです。

図16 。 原因の原因と指定

コンポーネントR-散逸要素


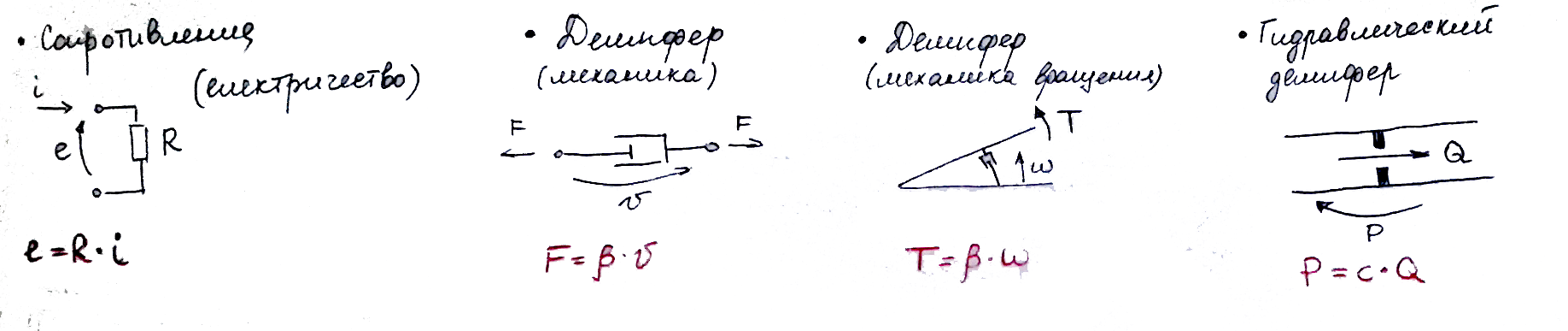コンポーネントI-慣性要素



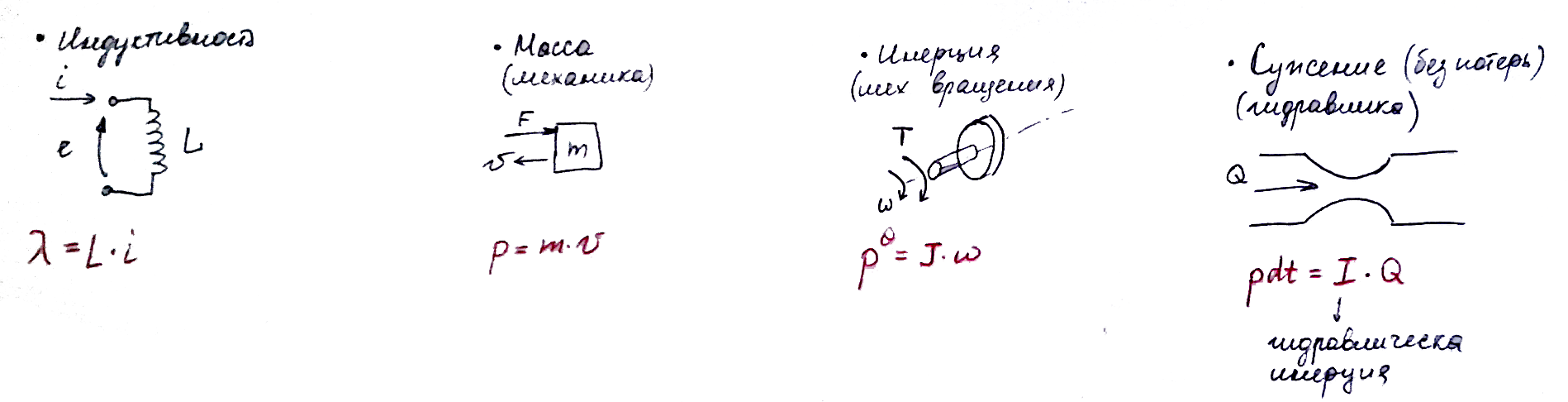コンポーネントC-容量性


図からわかるように、同じタイプR、C、Iの異なる要素は同じ方程式で記述されます。 静電容量には違いがあるだけで、これを覚えておく必要があります！

4ポートコンポーネント ：

トランスとジャイレータの2つのコンポーネントを検討してください。

1. Ideal Transformer （TF）は、入力と出力の間で1種類の値を接続します
   
   
   
   それぞれ図aとbのトランスフォーマーを記述する式：
   
   
   
   
   因果標識は、以下に示すようにのみ配置する必要があります。
   
   
   
   
   これは不可能です：
   
   
   
   
   
   機械領域の変圧器の例は、ギア、レバー

   
   
   
   従来の変圧器は電気にあります。 油圧ピストンは油圧になっています。
   
   
2. ジャイレーター （GY）。 理想的なジャイレータは、一方の流れを他方の努力と結び付けます。
   
   
   
   フォーミュラ
   
   
   
   ジャイレーターの許容可能な因果関係：
   
   
   
   誤った因果関係：
   
   
   
   ジャイレータの例：メカニクスでは、これはDCモーターで、エレクトロニクスでは-ソレノイド（リニアアクチュエータ）です。
   

ボンドグラフ法の最後の重要なコンポーネントは接続です。 ノードには2つのタイプがあります。

• タイプ0 （a）のノード -彼らは共通の努力をしており、1つの因果関係のみを0ノードに含める必要があり、残りは外に出なければなりません。
  
  
  
  0ノード計算の例を考えてみましょう：
  
  
  
  a）0はすべての努力が等しいことを意味します
  
  
  
  ノードは蓄積せず、エネルギーを消散しないため、入力電力の代数和はゼロでなければなりません。
  
  
  
  私たちが得る前の方程式を考慮に入れます
  
  
  
  b）2番目の
  
  
  
  
• タイプ1 （b）のノード -共通のフローがあり、1つの因果関係のみが外に出て、残りは1ノードになります。
  
  
  
  1ノード計算を検討する
  
  
  
  a）1つのノードに共通のスレッドがあります。つまり、
  
  
  
  ノードは蓄積せず、エネルギーを消散しないため、入力電力の代数和はゼロでなければなりません。
  
  
  
  前の方程式を考えると、次のようになります。
  
  
  
  b）ここにあります：
  
  
  
  

これでコンポーネントが完成しました。

ボンドグラフを作成した後、因果関係を付加する主な段階：

1. すべてのソースを添付
2. すべてのノードを調べて、段落1の後に因果関係を置きます
3. コンポーネントIには、入力因果関係を割り当てます（力はこのコンポーネントに含まれます）。 コンポーネントCには、出力因果関係を割り当てます（力はこのコンポーネントを離れます）
4. ステップ2を繰り返します
5. 接尾辞Rコンポーネント

これでミニ理論コースは終了です。 これで、モデルを構築するために必要なものはすべて揃いました。
いくつかの例を解きましょう。 電気回路から始めましょう。ボンドグラフの構築の類似性を理解することをお勧めします。



結論 ：私にとって、ボンドグラフはもっと面白そうだ。 私の観察によると、複雑なシステム（マルチドメインシステム、メカトロニクスシステム）に使用する方が良いとされています。 たとえば、強力なマルチドメインシミュレーターAMESimは、この方法を使用してマットモデルを構築します。 ロボット工学では、ラグランジュ法のほうが簡単です。 これらの方法を使用している人は、あなたの結論、コメントを聞いてうれしいです。

PS：コース資料へのリンク 。 （ラグランジュのスライド、債券グラフのスライド-主に紙の上にある本や抄録を使用）