O評価の不正確さについてあなたの問題を非難しないのはなぜですか

私はこの投稿とこの翻訳の最近の出版物からこの投稿を書くことに触発されました。著者はインテリジェントな形で、古典的な、一見、アルゴリズムの計算の複雑さのO推定が彼らの実際の開発経験と不調和になった方法に対する不満を表しています。 批判の主な主題は、これらの推定値が得られたフレームワークでのメモリモデルでした-それは、現代のコンピューターシステムで行われる速度の原理による階層組織の特徴を考慮していません。 そこからすべてのその後のトラブルが成長します。 そして、感謝された読者の観察された反応から判断すると、著者は彼らのinりと彼らのO-ビッグのもので古典に「走る」ことへの欲求において孤独からはほど遠いです。 だから、ランプのようにゆっくりと突っ込んでいる車のために作られた白いコートの叔父の物語を埋め立て地に送り、現代の「鉄」の解剖学をより正確に反映する若い野心的なモデルに道を譲るのは本当に価値がありますか？


理解しましょう

テキストの過程で、私は2番目の出版物とそれに関するいくつかのコメントを参照します。 生活のために触れた。 しかし、まず最初に、このテキストの過程で理解されていることについて同意しましょう。

定義を紹介します。 させる そして セットで定義されている2つの実関数 。 次に記録する そのような正の数があることを意味します みんなのために 正しく 。 この指定は -表記、およびOはバッハマン記号、または単に「 O-大」と呼ばれます。

この定義にはいくつかの結果があります。

1.すべての場合 起こる その後から 「それに続く 。 特に、定数を掛けてもO-推定値は変わりません。

簡単に言えば、 O-式に定数を掛けると、バッハマン記号がこの定数を「食べ」ます。 これは、 O-推定を含む式の等号は、値の古典的な「等式」として解釈できず、さらに洗練することなくそのような式に数学演算を適用できないことを意味します 。 そうしないと、次のような奇妙なものが得られます。 。 これは、バッハマン記号の背後に「隠れている」定数の意性の結果です。

2.もし に限定 、つまり、そのような数があります みんなのために 行った それから 。

数学からロシア語への翻訳と単純化のために 数直線の有限間隔、次があります： 与えられた間隔の関数が無限に行かない場合、それについて言うことができる最も無意味なことは、 O （1）に対応することです。 これは彼女の行動について何も新しいことを言っていません 。


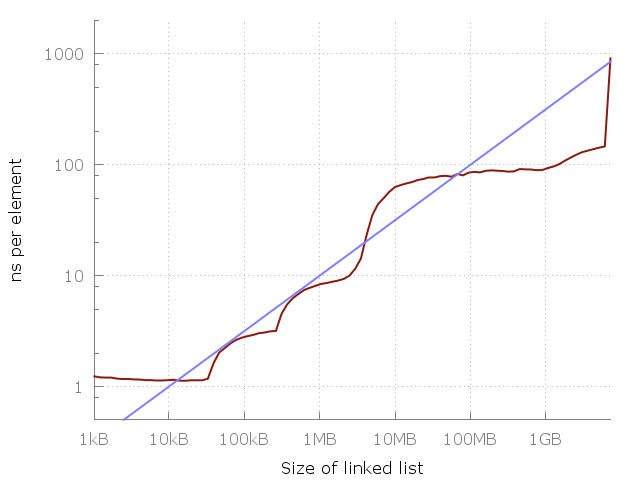
青い線はO（√N）です。

アルゴリズムの複雑さを推定する場合に戻り、引用された出版物の著者によって提供された写真を見てみましょう。 実行時間の増加を観察すると、O（1）推定値は支払不能であるという結論が導かれます。 しかし、プログラムの動作が分析される間隔は有限です。 したがって、実際には、推定値O（1）が悪いと主張されています。

まあ...ありがとう、キャップ。

さらに、さらに推測しようとします！ 大多数化関数は単純に曲線の形であり、「見た目が似ている」と彼らは言います。 アルゴリズム自体の分析を行わずに、焦点を合わせようとしている機能を考慮し、メモリモデルを導入しません！ そして、実際には、立方根ではなく平方根があるのはなぜですか？ それとも、ある種の対数ではありませんか？ まあ、正しい言葉で、彼らは少なくともいくつかのオプションを提供します、なぜすぐに「注意、正しい答え」ですか？

ここで予約する価値があります。 当然、プロセッサから「より遠い」ドライブに切り替えると、アクセス時間が低下するという誤った結論に至ることはありません。 ただし、メモリのランダムアクセスでデータの一部を受信する時間は、階層の最も遅いレベルであっても一定の値であるか、少なくとも制限されています。 これから、推定値O（1）が続きます。 また、制限がなく、データの次元に依存する場合、メモリへのアクセスは任意ではありません。 定義上、非常に愚かです。 理想的なアルゴリズム構造を扱っていることを忘れないでください。 したがって、「データセンターはHDDを超える」と言われると…紳士、これはどのようなランダムアクセスで、どのような配列とハッシュテーブルですか。 これはテーブルの下で詐欺と呼ばれます。あなたは静かにタスクの条件を変更し、前の質問に答えをもたらし、「Ahtung！ 間違っている！」 それは私にとって深刻な困惑の攻撃を引き起こします。 実際、 配列array 、 vectorまたは<some type>の後ろに*コンパイラーがクラスターのノード間で分散されたメモリーの一部を隠している場合、この構造はWirthとKnuthの本の配列ではなく、何でも構いません彼らにとって、これらの本に書かれた正式な分析の結果は非常に愚かな考えです。 統合失調症も同様に、すべての深刻さにおいて、評価の共通性について話します。これは、任意のテストの結果をグラフで見ることによって発明されました。

与えられた判断の誤りは、複雑さのO評価が実験に基づいて行われるという事実にあります。 これを強調するために、アルゴリズムの複雑さの推定に適用できるO記法のもう1つの「プロパティ」を紹介します。

3. O-推定は、アルゴリズムの構造の解析からのみ取得できますが、実験の結果からは取得できません。 実験の結果によると、統計的推定値、専門家の推定値、近似の推定値、そして最終的には工学的および審美的な喜びを得ることができますが、漸近的な推定値は得られません。

後者は、そのような推定の意味が、十分に大きいデータ次元に対するアルゴリズムの振る舞いを知ることであり、通常、その大きさは指定されていないという事実の結果です。 これは唯一ではなく、常に主要なものではありませんが、アルゴリズムの興味深い特徴です。 ダイクストラとホアールの時代では、次元3-6の次数は非常に大きいと考えられ、現在は10-100です（分析の深さを装っていない私の推定によると）。 言い換えれば、アルゴリズムの複雑度関数の漸近的推定値を取得するという問題を提起する場合、 O表記法の定義を次のように変更すると便利です。

させる 。 それから は、相互に独立した正の数Aとnがあり、すべての 行った 。

つまり、アルゴリズムの複雑さの分析では、実際には、左側に制限され、右側に制限されていないすべての区間の複雑度関数の主要な要素を考慮します。 これは、このようなO-推定値を任意に多く示すことができ、そのような推定値はすべて実用的に役立つことを意味します。 それらのいくつかは小さなNに対して正確ですが、すぐに無限になります。 他の人はゆっくりと成長しますが、彼らはそのようなNから始めて公平になります。 したがって、メモリへのアクセス時間の推定値が 構造解析が隠されている場合、この推定値は特定の範囲の次元で使用できますが、それでも推定値O（1）の忠実度はキャンセルされませんでした。

漸近的推定値の誤った比較の典型的な例は、正方行列乗算アルゴリズムです。 推定値の比較のみに基づいてアルゴリズムを選択する場合、ウィリアムズアルゴリズムを使用し、心配する必要はありません。 エンジニアリングの問題に特徴的な次元のマトリックスに適用することを決めた人にのみ創造的な成功を望むことができます。 しかし一方で、問題の特定の次元から始めて、Strassenアルゴリズムとそのさまざまな修正が些細なものよりも速く動作することはわかっています。これにより、問題を解決するアプローチを選択するときに操作の余地が与えられます。

愚かさは知性に由来する方法

O-評価の不正確さを犯すことは、これらの推定値の意味を完全に理解しないことを意味し、もしそうなら、誰もそれらを使用することを強制しません。 お住まいの地域に固有のデータセットのテストの結果として得られた統計的推定値を優先することは、かなり可能であり、しばしば正当化されます。 漸近解析としてこのような繊細な楽器を文盲で使用すると、過剰になり、一般的に驚くべきことが起こります。 たとえば、 O表記を使用すると、並列プログラミングの考え方の矛盾を「」「証明」「」できます。

次元Nのデータの一部が供給され、連続して実行されたときに複雑なアルゴリズムがあるとします は、簡単かつ無条件に同じ独立したNに分割され、簡単にするために、計算と時間の複雑さが同じ部分に分割されます。 そのような各部分の複雑さは 。 M個の独立した計算機があるとします。 並列アルゴリズムを実行することの全体的な複雑さは、 。 アルゴリズムの複雑さの漸近的推定は、有限数のプロセスへの完全な並列化の結果としても変化しないことが判明しました。 しかし、熱心な読者は、バッハマンのシンボルがハミングアップしていた「隠された」定数が変化したことに気づきました。 つまり、並列化の概念に関するこのような分析から一般的な結論を引き出すことは、少なくともばかげています。 しかし、別の極端なことも可能です-もちろん、プロセッサの数が並列処理の無限のリソースに基づいて、「アルゴリズムの並列バージョン」の評価がO （1）であると断言することを忘れてください。

まとめると

結論として、次の魅力的な新規性ステートメントを提供できます。

• O-推定値の単純な比較に基づいて、あるアルゴリズムが別のアルゴリズムよりも効率的であると主張することはできません。 このようなステートメントには、常に説明が必要です。
  
  
• このような推定値の正確性または不正確性に関するパフォーマンス測定の結果から結論を出すことは不可能です。隠された定数は通常不明であり、非常に大きくなる可能性があります。
  
  
• そのような推定値をまったく使用せずに、アルゴリズムとデータ構造について話すことができます（必要な場合もあります）。 これを行うには、興味のある特定のプロパティを言うだけです。
  
  
• ただし、使用するアルゴリズムの特性などを考慮して、特定のエンジニアリングの決定を行うことをお勧めします。

漸近的推定が不正確、不正確、または非実用的であるという主張は、提起された問題の通常の予備分析を行うことを嫌がり、名前に頼ろうとする試みによって隠されますが、扱われる抽象の本質ではありません。 アルゴリズムの漸近的な複雑さについて話すと、有能な専門家は、理想化された構造について話していることを理解し、それらを実際の「ハードウェア」に投影する正確さの程度を念頭に置いて、「一般的に」という言葉から、それだけに依存するエンジニアリングの決定を決して受けません 。 O-評価は、新しいアルゴリズムを開発し、複雑な問題の根本的な解決策を見つける際により有用であり、特定のハードウェア用の特定のプログラムを作成およびデバッグする際にはあまり有用ではありません。 しかし、それらを誤って解釈し、スマートブックで読んだ内容の理解があなたに約束したものをまったく受け取らなかった場合、これらの推定値の証拠を受け取った人にとってこれは問題ではないことを認めなければなりません。