この記事は、クラスタリングについてであり、CRANに最近追加された
ClusterRパッケージです。 以下の詳細と例は、主にVignetteパッケージに基づいています。
クラスター分析またはクラスター化は、あるグループ内のオブジェクト(クラスターと呼ばれる)が他のグループ(クラスター)のオブジェクトよりも(ある意味では)互いに類似するように、オブジェクトのセットをグループ化するタスクです。 これは、研究データ分析の主要なタスクの1つであり、以下を含むさまざまな分野で使用される標準的な統計分析手法です。 機械学習、パターン認識、画像分析、情報検索、バイオインフォマティクス、データ圧縮、コンピューターグラフィックス。
クラスタリングアルゴリズムの最も有名な例は、
接続ベースのクラスタリング (階層的クラスタリング)、
中心ベースのクラスタリング (k-means法、k-medoid法)、
分布ベースのクラスタリング (GMM-Gaussian混合モデル)、および
密度 (DBSCAN-ノイズを伴うアプリケーションの密度ベースの空間クラスタリング-密度に基づくノイズを伴うアプリケーションの空間クラスタリング、OPTICS-クラスタリング構造を識別するための順序点-クラスタリング構造を決定するための順序点など)
最初の部分 :分布のガウス混合(GMM)、k-means法、ミニグループのk-means法。
K-medoid法
k-medoidアルゴリズム (L. Kaufman、P. Russo、1987)は、k-meansアルゴリズムおよびmedoid変位アルゴリズムと共通のクラスタリングアルゴリズムです。 k-meansとk-medoidsのアルゴリズムは分離されており、どちらも同じクラスターからの点とこのクラスターの中心によって指定された点の間の距離を最小化しようとします。 k-meansアルゴリズムとは異なり、k-medoidメソッド
はデータセットからポイントを中心 (medoidまたは標準)
として選択し、
ポイント間
の距離の任意のメトリックで機能します。 kを決定するための便利なツールは、輪郭の幅です。 k-medoid法は、2乗ユークリッド距離の合計ではなく、ペアワイズ偏差の合計を最小化するため、k-meansよりもノイズと異常値に対して耐性があります。 medoidは、クラスター内の他のすべてのオブジェクトからの平均偏差が最小のクラスターのオブジェクトとして定義できます。 これは、クラスターの中心に最も近いポイントです。
k-medoidクラスタリングの最も一般的な実装は、Partitioning Around Medoids(PAM)アルゴリズムです。 RAMには、「ビルド」(ビルド)と「再配置」(SWAP)の2つのフェーズがあります。 BUILDフェーズでは、アルゴリズムは初期medoidの適切なセットを検索し、SWAPフェーズでは、目的関数が減少しなくなるまで、BUILD medoidと値の間のすべての可能な移動が実行されます(オブジェクト指向環境でのクラスタリング、A.Shtruyf、M.Hubert 、P。Russo、1997)。
ClusterRパッケージでは、関数
Cluster_Medoidsおよび
Clara_MedoidsはPAM(medoidの周りのパーティション分割)およびCLARA(大規模アプリケーションのクラスタリング)アルゴリズムに対応しています。
次のコード例では、
マッシュルームデータを使用して、ユークリッド以外の距離メトリックでk-medoidメソッドがどのように機能するかを示します。
マッシュルームデータは、23のカテゴリ属性(クラスを含む)と8124値で構成されています。 パッケージのドキュメントには、このデータに関する詳細が記載されています。
Cluster_Medoids
入力として、
Cluster_Medoids関数は(データ行列に加えて)偏差行列も受け入れることができます。 すべての変数がカテゴリ(2つ以上の一意の値)であるマッシュルームデータの場合、
ガウアー距離を使用することは理にかなっています。 距離
ガワーは、タイプ(数値、順序付き、および順序なしリスト)に応じて、さまざまなインジケーターにさまざまな機能を使用します。 この偏差メトリックは、クラスターパッケージ(
デイジー機能)およびFDパッケージ(
gowdis機能)の中でも特に、多くのRパッケージに実装されています。 FDパッケージの
gowdis関数を使用します。これにより、ユーザー定義の重みを別の要素として設定することもできます。
data(mushroom) X = mushroom[, -1] y = as.numeric(mushroom[, 1])
| adjust_rand_index | avg_silhouette_width |
|---|
| 0.5733587 | 0.2545221 |
前述のように、FDパッケージの
gowdis関数を使用すると、ユーザーは個々の変数に異なる重みを設定できます。 たとえば、
ランダム検索を使用して、より良いクラスタリング結果を実現するなど、重みを調整できます。 たとえば、個々の変数のこのような重みを使用すると、
調整済みランドインデックス (外部検証)と
平均シルエット幅 (平均輪郭幅、内部検証)の両方を改善できます。
| 予測因子 | 重り |
|---|
| cap_shape | 4.626 |
| cap_surface | 38.323 |
| cap_color | 55.899 |
| あざ | 34.028 |
| 臭い | 169.608 |
| gill_attachment | 6.643 |
| gill_spacing | 42.08 |
| gill_size | 57.366 |
| gill_color | 37.938 |
| stalk_shape | 33.081 |
| stalk_root | 65.105 |
| stalk_surface_above_ring | 18.718 |
| stalk_surface_below_ring | 76.165 |
| stalk_color_above_ring | 27.596 |
| stalk_color_below_ring | 26.238 |
| veil_type | 0.0 |
| veil_color | 1.507 |
| リング番号 | 37.314 |
| リングタイプ | 32.685 |
| spore_print_color | 127.87 |
| 人口 | 64.019 |
| 生息地 | 44.519 |
weights = c(4.626, 38.323, 55.899, 34.028, 169.608, 6.643, 42.08, 57.366, 37.938, 33.081, 65.105, 18.718, 76.165, 27.596, 26.238, 0.0, 1.507, 37.314, 32.685, 127.87, 64.019, 44.519) gwd_w = FD::gowdis(X, w = weights)
| adjust_rand_index | avg_silhouette_width |
|---|
| 0.6197672 | 0.3000048 |
Clara_Medoids
CLARA (大規模アプリケーションのクラスタ化-大規模アプリケーションのクラスタリング)は、大規模データセットのクラスタリングに適した選択肢です。 データセット全体のmedoidを検索する代わりに-不一致マトリックスの計算も不可能なタスクです-CLARAは小さなサンプルを取得し、PAMアルゴリズム(Partitioning Around Medoids)を適用して、このサンプルのmedoidの最適なセットを生成します。 得られたmedoidの品質は、データセット内の各オブジェクトとそのクラスターのmedoidの平均の非類似性によって決まります。
ClusterRパッケージの
Clara_Medoids関数は同じロジックを使用し、
Cluster_Medoids関数を各サンプルに適用します。
Clara_Medoidsはさらに2つのパラメーター、
samplesおよび
sample_sizeを受け入れます。 1つ目は、元のデータセットから形成する必要があるサンプルの数を決定し、2つ目は、サンプル形成の各反復におけるデータの割合(0.0〜1.0の小数)を決定します。
Cluster_Medoids関数と
は異なり、
Clara_Medoids関数は不一致マトリックスを入力として受け入れないことに
注意してください 。
以前に使用した
マッシュルームデータセットにClara_Medoids関数を適用し、
ハミング距離を不一致メトリックとして、計算時間と結果を
Cluster_Medoids関数の結果と比較します。
ハミング距離は、次のように
キノコデータに適しています。 離散変数に適用可能であり、2つの比較されたインスタンスに対して異なる値をとる属性の数として定義されます(「データマイニングアルゴリズム:Rによる説明」、Powell Chikosh、2015、p。318)。
cl_X = X
| adjust_rand_index | avg_silhouette_width |
|---|
| 0.5944456 | 0.2678507 |
start = Sys.time() cl_e = Cluster_Medoids(cl_X, clusters = 2, distance_metric = 'hamming', swap_phase = TRUE, verbose = F, threads = 1) end = Sys.time() t = end - start cat('time to complete :', t, attributes(t)$units, '\n')
| adjust_rand_index | avg_silhouette_width |
|---|
| 0.5733587 | 0.2545221 |
ハミング距離を使用すると、
Clara_Medoidsと
Cluster_Medoidsは(
ガウアー距離の結果と比較して)ほぼ同じ結果を返しますが、
Clara_Medoids関数はこのデータセットの
Cluster_Medoidsより4倍以上高速です。
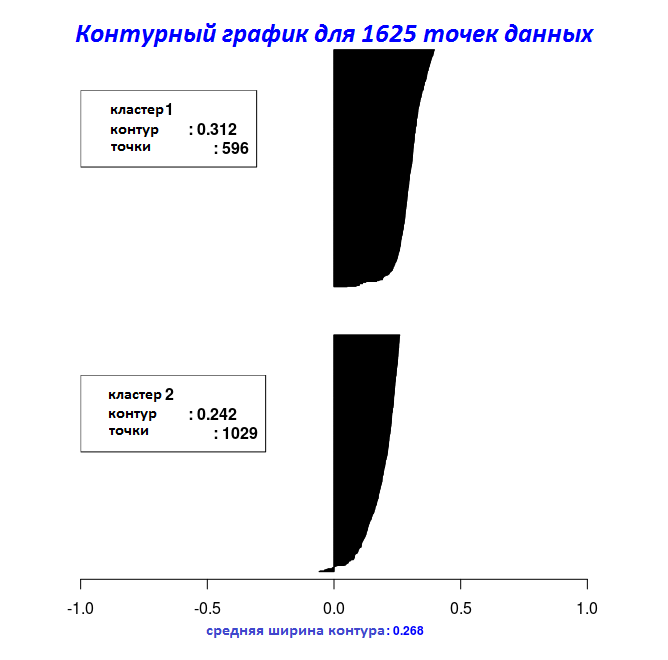
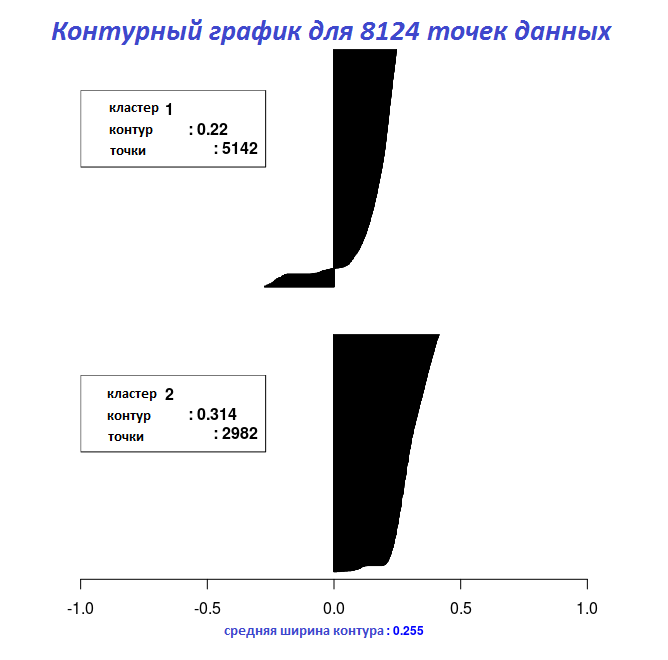
最後の2つのコードフラグメントの結果を使用して、
Silhouette_Dissimilarity_Plot関数を使用して、グラフに等高線の幅をプロットできます。 ここで言及する価値があるのは、
Clara_Medoids関数の輪郭の非類似性と幅は、
Cluster_Medoids関数の場合のように、データセット全体ではなく、最良の選択に
基づいていることです。
k-Medoid関数のリンク
k-medoidの関数(
Cluster_Medoidsおよび
Clara_Medoids )の実装には、最初は最初のmedoidがk-meansアルゴリズムの中心と同じ方法で初期化されると思ったため、かなり時間がかかりました。 なぜなら KaufmanとRussoの本にはアクセスできませんでした。詳細なドキュメントを含む
クラスターパッケージは大いに役立ちました。 必要に応じて、アルゴリズム、PAM(Medoidのパーティション分割-Medoidの分離)、およびCLARA(大規模アプリケーションのクラスタリング-大規模アプリケーションのクラスタリング)の両方が含まれ、結果を比較できます。
次のコードフラグメントでは、前の量子化の例に基づいて、
クラスターパッケージのpam関数
と、ClusterRパッケージのCluster_Medoidsおよび受信したmedoidsを比較します。
# [,1] [,2] [,3] # [1,] 1.0000000 1.0000000 1.0000000 # [2,] 0.6325856 0.6210824 0.5758536 # [3,] 0.4480000 0.4467451 0.4191373 # [4,] 0.2884769 0.2884769 0.2806337 # [5,] 0.1058824 0.1058824 0.1058824
# [,1] [,2] [,3] # [1,] 0.2884769 0.2884769 0.2806337 # [2,] 0.6325856 0.6210824 0.5758536 # [3,] 0.4480000 0.4467451 0.4191373 # [4,] 0.1058824 0.1058824 0.1058824 # [5,] 1.0000000 1.0000000 1.0000000
# [,1] [,2] [,3] # [1,] 0.2863456 0.2854044 0.2775613 # [2,] 1.0000000 1.0000000 1.0000000 # [3,] 0.6325856 0.6210824 0.5758536 # [4,] 0.4480000 0.4467451 0.4191373 # [5,] 0.1057339 0.1057339 0.1057339
このデータセット(5625行と3列)の場合、OpenMPが使用可能な場合(6ストリーム)、
Cluster_Medoids関数は
pam関数のほぼ4倍の速度で同じmedoidを返します。
ClusterRパッケージの現在のバージョンは、私の
Githubリポジトリで入手できます。バグレポートについては、
このリンクを使用し
てください 。