壮大な戦いで巨大な軍隊が戦場に集結する映画は、通常、人々の感情の嵐を引き起こします。 見事に装備されたライトセーバージェダイとバトルドロイドの大群とのスターウォーズバトルも例外ではありません。
しかし、戦闘プロセス自体を鳥瞰図のように見て、イベント全体を見るのは面白いこともあります。 これを行うには、さまざまな仮想シミュレーションツールを使用できます。 この投稿では、セルラーオートマトンなどの単純な離散モデルを使用して、連邦戦闘ドロイドとジェダイオーダーの間の戦闘をモデル化する例を示します。

セルオートマトン
全世界がセルと呼ばれる正方形に分割されたグリッドであると想像してください。 これらの各セルは、指定されたセットから異なる状態になります。 通常、次数1のムーア近傍によって決定される隣接セルの状態は、セルの状態に影響します。 そのようなモデルの鮮明な例は、1970年代に数学者ジョン・コンウェイによって発明されたゲーム「Life」です。 そのルールは非常に簡単です。
- 各セルは、「ライブ」または「デッド」のいずれかです。
- 死んだ細胞は、隣にちょうど3つの生きた細胞があり、次の動きで生きたものになります。
- 生きている細胞の隣に2つまたは3つの生きている細胞がある場合、次の動きは生き続けます。
- 生細胞の隣に2個未満または3個以上の生細胞がある場合、死にます。
セルオートマトンを使用して壮大な戦いをシミュレートするのは、このようなモデルのルールの記述の単純さのおかげです。
あなたの機械を発明します
合計で、セルラーマシンには4種類のセルがあります。フィールド(緑)、ドロイド(ベージュ)、ジェダイ(青)、ブラスター(赤)です。 次に、ルールを考え出します。 ジェダイのビームを積み上げて爆破するにはドローンが必要であり、ジェダイはこれらの密集したドロイドを攻撃します。 モデリングを簡単にするために、セルに新たな機会を追加します-動き回る。 実際、セルオートマトンでのセルの移動は、セルの1つが遷移状態に遷移し、遷移自体がゼロ状態(この場合はこのフィールド)に移行することとして定義できます。
戦闘シミュレーターを作成するために実装する必要があるもの:
- ドロイドはグループになります
- ドロイドが射程内の近くのジェダイを攻撃
- ジェダイは彼に最も近いユニットを攻撃します
ドロイドグループの検索
ドロイドがグラフの頂点として表され、隣接するドロイドが接続された頂点として表される場合、ドロイドグループはそのようなグラフの接続されたコンポーネントです。 詳細な検索(DFS)を使用して、各ステップの最後で簡単に取得できます。
components = [] var colors = new Array(field.grid.length) colors.fill(0)
接続されたコンポーネントを決定する関数自体は再帰的です:
function dfs(colors, v) { colors[v] = 1 var x = field.grid[v].x, y = field.grid[v].y, k = 1 for (var i = 0; i < field.grid[v].n.length; i++) if (field.grid[field.grid[v].n[i]].color == 1 && colors[field.grid[v].n[i]] == 0) { var newPos = dfs(colors, field.grid[v].n[i]) x += newPos.x y += newPos.y k += newPos.k } colors[v] = 2 return { x: x, y: y, k: k } }
プロパティkは、グループ内のドロイドの数に対応し、グループの中心(各ドロイドのx座標とy座標の算術平均)を計算するために必要です。 各ドロイドは、その座標を最初の再帰呼び出しに転送します。その呼び出しは、すべてのドロイド座標の合計とその数を返します。
ゴールゴール
戦闘のすべての参加者には目標があります-ヒットしようとするセル:最寄りのドロイドグループの中心にあるジェダイ、同盟国にいるドロイド、ジェダイが射撃された瞬間の座標を持つセルにある発射体。
function moveToTarget(n, me, priority, ban) { var newX = me.x, newY = me.y var deltaX = me.tx - me.sx, deltaY = me.ty - me.sy var scope = deltaY / deltaX if ((deltaX == 0) || (deltaY == 0)) { newX = me.x + (deltaX == 0 ? 0 : deltaX / Math.abs(deltaX)) newY = me.y + (deltaY == 0 ? 0 : deltaY / Math.abs(deltaY)) } else { if (Math.abs(scope) >= 1) { newY = me.y + deltaY / Math.abs(deltaY) newX = me.sx + Math.round((newY - me.sy) / (scope)) } else { newX = me.x + deltaX / Math.abs(deltaX) newY = me.sy + Math.round((newX - me.sx) * (scope)) } } if (!set(n, { x: newX, y: newY }).length) { me.color = 0 return false } var newCell = set(n, { x: newX, y: newY })[0] for (var key in ban) if (newCell[key] == ban[key]) return false return { x: newX, y: newY, instead: { color: 0 }, priority: priority } }
仕組みを見てみましょう。 ターゲットとX軸に沿ったオブジェクトの初期位置との間の距離は、deltaXによって示され、Y軸に沿ってdeltaYによって示されます。 オブジェクトの初期x座標の値がターゲットの座標よりも大きい場合、deltaXが負になることは明らかです。 deltaYについても同じことが言えます。
スコープとしてdeltaYとdeltaXの比率を示します。 勾配が1より大きい場合、各ステップでオブジェクトはY軸に沿って1つ、場合によってはX軸に沿って1つずつシフトされますnewY = me.y + deltaY / Math.abs(deltaY)、絶対値で除算すると正しい単位を取得できますおなじみ。 動きは次のように定義できるため
x = y / scope、次にnewX = me.sx + Math.round((newY-me.sy)/(scope))。 スコープ<1の場合にも同じことを行います。
オブジェクトとターゲットが同じ列または同じ行にある場合があります。 その後、ゼロによる除算が発生する場合があります。 そのような場合、チェックが行われます(deltaX == 0)|| (deltaY == 0)。 これが当てはまる場合、三項演算子を使用して座標の差を確認し、その値がゼロ以外の場合は、正しい符号を持つユニットを追加します。
banパラメーターには、オブジェクトの移動先のセルでは受け入れられないプロパティが含まれています。 たとえば、ドロイドは他のロボットにぶつかってはいけません。 したがって、ドロイドの場合、ban = {color:1}(1はドロイドのカラーインデックスです)。 オブジェクトの移動先のセルに、同じ名前の禁止プロパティと同じ値を持つプロパティが少なくとも1つある場合、移動はありません。
オブジェクトが存在しないセル(フィールドの境界を越えて移動する)に到達しようとすると、マップから消えます。
しかし、すべてがうまくいった場合、関数は新しい座標としてnewXとnewYを返します。
ドロイドアルゴリズム
ドロイドは最も近いジェダイに向かって発射します。 ドロイドの可視半径は、係数k2で与えられます。 ドロイドは、最も近いジェダイ、長さ5の半径内でドロイドを傷つけないショットを選択します。
係数k2-ジェダイドロイドの距離検出。
ジェダイアルゴリズム
ジェダイのストライキの最適な方向を計算するには、周囲の各セルに対応する重みを設定します。これは次のように計算します。
ジェダイは8つのセルを囲みます(ジェダイがコーナーまたはフィールド境界の近くにある場合-3または5セル)。 重量はこれらのセルごとに個別に計算され、ジェダイ周辺の残りのセルの状態に依存します。 5 a1 + 4 b1 + 4 b2 + 3 c1 + 3 c2 + 2 d1 + 2 d2 + 1 eの形式の重みとして重みを表します。対応するセルがドロイドによって占有されている場合、各変数は1に等しく、それ以外の場合はゼロです。 処理されたセルからセルが遠いほど、対応する単項式の係数は低くなります。
セルの重みの計算の例を図に示します。

特定の状況でのセルの重み:
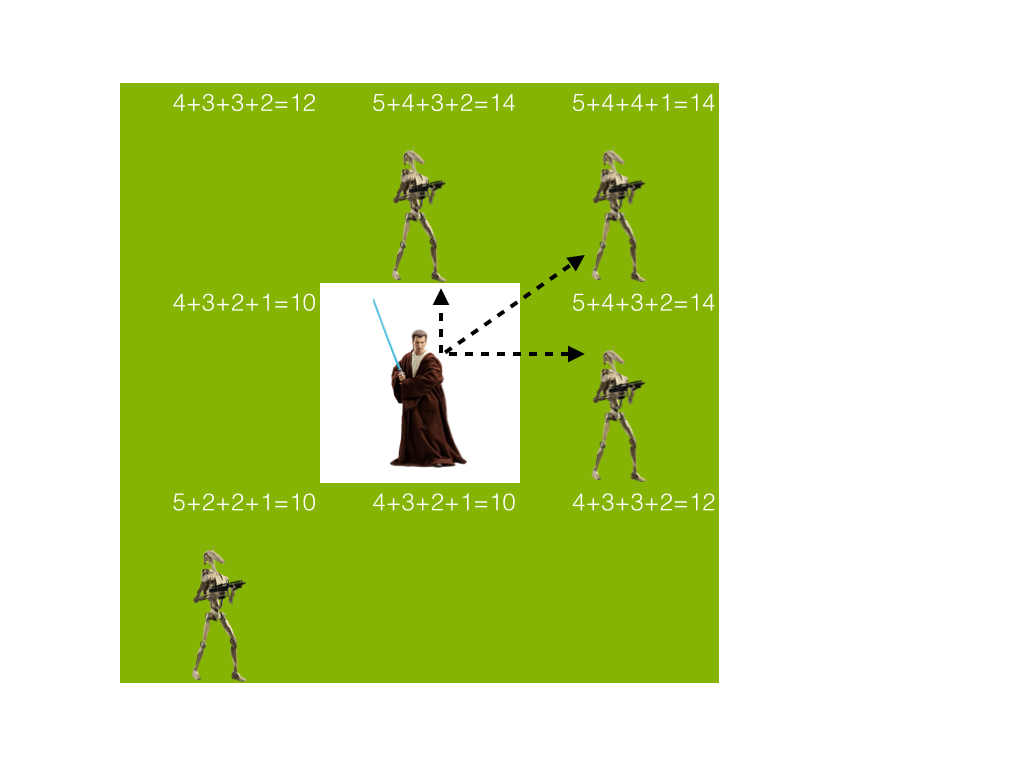
この場合、ジェダイには3つの最適な移動オプションがあります。 それらの1つがランダムに選択されます。
ジェダイがドロイドのクラスターを検出するのを助けるために残っています。 ドロイドがドロイドに近接している場合に接続されているグラフの頂点として想像すると、各ステップの後、深さ検索(DFS)を使用して、このグラフのすべての接続されたコンポーネントを見つけ、それらの中心の座標と配列内のコンポーネントのドロイドの数を書き込むことができます 次のステップで、ジェダイは最も近いユニットを検索し、すぐにそれらに突進します。
係数k1は、ジェダイが回避できるシェルの最大数です。 デフォルトでは、k1 = 4です。
発射物飛行
無限のシェルは飛ぶことができないため、32ステップ後に消えます。
function processBullet(n, me) { me.age++ if (me.age > 32) me.color = 0 }
その動きは非常に簡単です-目標への方向の関数の通常の呼び出し:
function moveBullet(n, me) { return moveToTarget(n, me, 1, {}) }
厄介なチップ
厳密に定義されたアルゴリズムを正式に実行するプログラムは、奇妙な結果で私たちを驚かせることがあります。
最も注目すべきは「死んだジェダイ効果」です。 ジェダイは死んで立ち上がっています。


なんで? 答えは簡単です。ジェダイの1人が目標を達成し、群衆から脱出しようとしていますが、ジェダイの残りの部分は彼がこれを行うことを妨げています。 彼らは順番にターゲットに押し込もうとしていますが、それは忙しく、そこにいるジェダイはそれを離れることができないため、この状況が発生します。
戦闘をシミュレートします
ブラウザでシミュレーションを直接プレイできます。 セルのタイプを選択し、目的の場所が得られるまで画面上にセルの描画を開始します。 「開始」をクリックして、戦いをお楽しみください。 戦闘が終わった場合や退屈した場合は、「停止」から開始できます。その後、スケジュールが生成されます。 1つ目は特定の時点でのドロイドの数を示し、2つ目はジェダイの同じ統計を示します。
» ここでシミュレーションを試すことができます
チャートを作成するために、 Chart.jsライブラリが使用されました 。 グラフは何を語っていますか?
- ドロイドの数は、特定のポイントまで同じままでした。 その時点で、ドロイドの数が減少し始めたとき、ジェダイとドロイドの間で最初の衝突が発生しました。
- ジェダイの最も一般的な死。 戦闘機は、敵のランクに身を寄せる前に発射体に当たったのですか、それとも、数値的に優位な敵に囲まれた戦闘の最中に倒れたのですか? これはすべて、2つのグラフで彼の死の瞬間を比較することで見つけることができます。
- 戦いの全体像。 彼はスムーズに歩きましたか、それとも「休息」と「クライマックス」がありましたか? グラフに急激なジャンプがあるかどうかを確認し、質問の答えを見つけましょう!
おわりに
コメント付きのソースコードはGitHubで入手できます 。 開始するには、リポジトリをダウンロードし、ブラウザでindex.htmlを開きます。
私の意見では、それは面白い光景でした。 チャートを使用すると、さまざまな初期構成での戦闘の進行に関する情報を収集できます。 実際の歴史的な戦いのグラフはどのように見えるのだろうか? もちろん、この投稿では架空の宇宙を調べていますが、実際の歴史的な戦いは同じルールに従って行われました。兵士はグループに集まり、お互いを攻撃し、もちろん損失を被りました。
ただし、1つのシミュレーションに限定するべきではありません。結局のところ、さらに興味深いタスクがあります。つまり、戦闘の各参加者に最適なアクションアルゴリズムを見つけることです。 そして、ここでゲーム理論が研究者を助けます。 しかし、これは全く異なる話です...