多くの場合、ニューラルネットワークでの作業中に、画像を含むクラスを分離するための線形決定関数(LRF)を構築するタスクに直面します。
図1. 2次元の場合この問題を解決する方法の1つは、最小二乗平均誤差アルゴリズム(NSCFアルゴリズム)です。
このアルゴリズムは、必要なLRFを構築するのに役立つという点だけでなく、クラスが線形に分離できない状況が発生したときに、誤った分類エラーが最小になる傾向があるLRFを構築できるという点で興味深いです。
図2.線形に分離できないクラス次に、ソースデータをリストします。

-クラス指定(i-クラス番号)

-トレーニングサンプル

-ラベル(画像が属するクラス番号
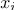
)

-学習速度(任意の値)
この情報は、LRFを構築するのに十分以上です。
アルゴリズム自体に直接進みます。
アルゴリズム
1ステップ
a)翻訳する

システムに

どこで

等しい

画像クラスは最後に割り当てられます
例:
画像を与えてみましょう

。
それから
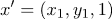
もし

クラス1から

もし

クラス2から
b)マトリックスを構築する

ベクトルで構成される次元Nx3

c)私たちは構築しています

d)考慮します

どこで
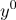
任意のベクトル(デフォルトの単位)
e)

(反復番号)
2段階
ブレーク条件を確認します。
もし
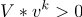
その後、停止
それ以外の場合は、手順3に進みます
3ステップ
a)
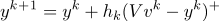
(+はヘビサイド関数です)
例(Heaviside関数):
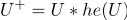
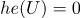
(もし
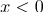
)
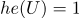
(もし
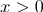
または

)
計算後、反復回数を変更します。
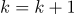
b)ステップ2に進む
NCOAアルゴリズムの例

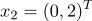
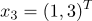
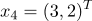
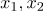
クラス1に属する
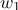

クラス2に属する

a)




b)

c)

d)
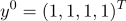
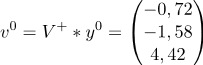
e)


なぜなら すべての要素


止まる
アルゴリズムが完成し、LRFを計算できるようになりました。

オンラインエディターの
parpalakに感謝します。
ご清聴ありがとうございました。