プログラマーとして、車を買いました。 パートII

前の記事で、モスクワで最大150万ルーブル相当の2010年以下のメルセデスベンツEクラスを購入する例では、収益性の高い車を見つける問題が考慮されました。 「収益性の高い」とは、ロシア連邦で中古車を販売するための最も評判の高いすべてのサイトから収集された広告の中で、価格が現在の市場価格よりも低いオファーを理解することです。

最初の段階では、機械学習法として多重線形回帰が選択され、その使用の正当性、および長所と短所が考慮されました。 単純な線形回帰が、馴染みのあるアルゴリズムとして選択されました。 明らかに、回帰問題を解決するためのより多くの機械学習方法があります。 この記事では、調査中のモデルに最適な機械学習アルゴリズムをどのように選択したかを正確に説明したいと思います。これは、現在実装しているサービス-robasta.ruで使用されています。

アルゴリズムの選択

「チャンピオン」のタイトルの申請者：

• 多重線形（単純）回帰
• なげなわ回帰
• リッジ回帰
• ロバスト回帰
• ボウパルウサギ
• 多項式および非線形回帰
• ランダムフォレスト
• Xgboost

選択を行う前に、上記のアルゴリズムはすべて調査されたため、各アルゴリズムについて詳しく説明したいと思います。 ただし、このようなブルー​​トフォース検索パスは完全に最適なものではなく、最初にタスクの追加調査を実施する方が合理的です。

メルセデス・ベンツEクラスに加えて、私はアウディA5に感銘を受けました。特に239馬力のディーゼルエンジンは、優れたダイナミクス（6秒から100 km / h）と許容税を備えています。 このドイツ人エンジニアの創造のエンジン出力への価格の依存関係を見ると（以下の視覚化）、多くの疑問が自然に消えます。

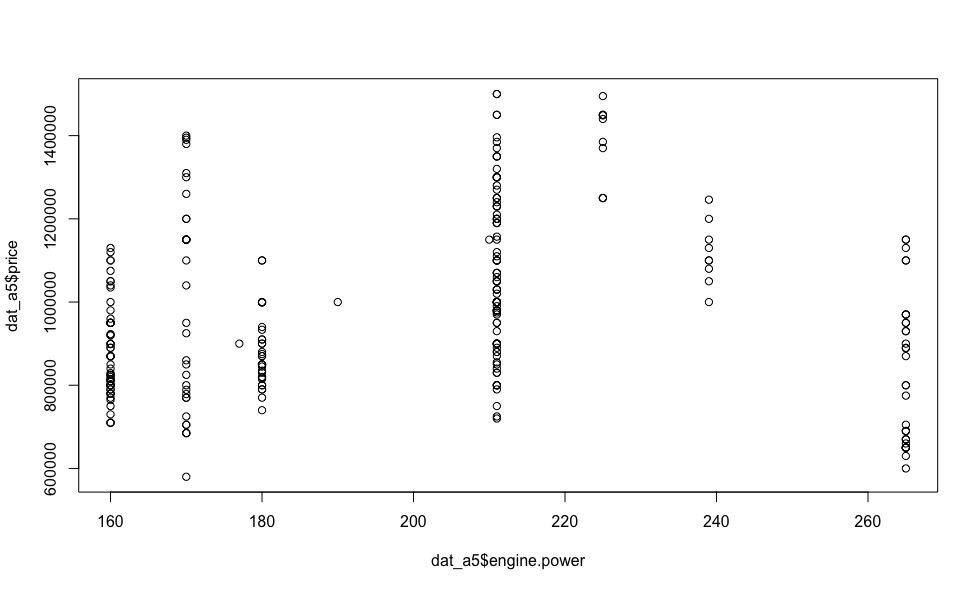
ここで線形依存の問題はないため、説明された変数（この場合はコスト）の回帰変数への線形依存に基づくアルゴリズムは安全に破棄できます。 多項式モデルと非線形モデルの使用は、特定の回帰モデルの個々の自動車モデルの価格への依存のタイプが事前にわからないという理由で違法です。

したがって、上記の考慮事項を考慮に入れると、 決定木に基づくアルゴリズム- ランダムフォレストとXgboost （2種類のブースティング-xgbDart、xgbTree）のみを考慮し、それらから最適なアルゴリズムを選択できます。

最適なアルゴリズムは、 交差検証および遅延サンプリング中に最高のパフォーマンス （最小RMSE ）を示すアルゴリズムであることに注意してください。
選択したアルゴリズムの「ブラインド」アプリケーションに進む前に、次の章で、それらの設定の問題について詳しく説明します。

相互検証

クロス検証（CV）は、モデルの実際の機能を評価し、機械学習タスクでそのパラメーターを調整するためによく使用されます。 初期サンプルの特定のパーティションセットは、トレーニングサブサンプルとコントロールサブサンプルに区別されます。 パーティションごとに、トレーニングサブサンプルに従ってアルゴリズムが構成され、その平均誤差がコントロールサブサンプルで推定されます。

交差検定評価は、コントロールサブサンプルのコントロールサブサンプル全体の平均誤差を指します。

交差検定で得られたエラーの確率のバイアス推定では 、 再トレーニングの現象を回避するために、トレーニングサンプルとコントロールサンプルが互いに素なサブセットを形成する必要があります。

交差検定の種類：

1. k分割交差検定
   
   
   詳細

   この方法は、データをランダムに、ほぼ同じサイズのk個のばらばらのブロックに分割します。 各ブロックは検証サンプルと見なされ、残りのk-1ブロックはトレーニングサンプルと見なされます。 モデルはk-1ブロックでトレーニングされ、検証ブロックを予測します。 モデルの予測は、選択したインジケータを使用して推定されます：精度、標準偏差（RMSE）など。 このプロセスはk回繰り返され、モデルの最終的な推定である平均値が計算されるk個の評価が得られます。 通常、kは10、時には5に選択されます。kが元のデータセットの要素の数に等しい場合、この方法は個々の要素の相互検証と呼ばれます（この記事は考慮されません）。
   
   
   
2. k倍交差検証の繰り返し。
   
   
   詳細

   この方法では、kブロックの交差検証が数回実行されます。 たとえば、5x 10ブロックの相互検証では50の評価が与えられ、それに基づいて平均評価が計算されます。 これは、50ブロックの相互検証とは異なることに注意してください。
   
   
   
3. モンテカルロクロス検証（MKKV、モンテカルロクロス検証、脱退グループクロス検証）。
   
   
   詳細

   このメソッドは、元のデータセットを、指定された回数、事前に決められた割合でトレーニングおよび検証サンプルにランダムに分割します。
   

上記の相互検証方法はそれぞれ、バイアスと分散を使用して特徴付けることができます。 バイアスは、評価の精度を特徴付けます。 分散は精度を特徴づけます。

一般に、相互検証方法のバイアスは、検証サンプルのサイズに依存します。 検証サンプルのサイズが初期データの50％である場合（2ブロックの交差検証）、標準偏差の最終推定値は、このサイズが初期データの10％である場合よりも偏りが大きくなります。 一方、検証サンプルのサイズが小さくなると、各検証サンプルに含まれるデータが少なくなり、安定した標準偏差が得られるため、分散が増加します。

したがって、kブロックの交差検証に関しては、バイアスを最小限に抑え、最大kを選択し、分散を減らすには、複数のkブロックの方法を使用します。

MQCEに関しては、検証サンプルのサイズは、このタイプの相互検証の分散に対する影響が、プロセスの繰り返し数よりもわずかに大きくなります。 また、プロセスの繰り返し回数がバイアスに大きく影響しないことにも注意してください。

したがって、MQWメソッドに小さいサイズの検証サンプル（たとえば、10％）を使用し、分散を減らすために多数の繰り返しを実行することをお勧めします。

ただし、Ceteris paribusでは、複数の10ブロックHFを使用すると分散が少なくなります。これは主に、この方法では、MQWとは異なり、同じデータ要素を異なるサンプルで見つけることができないためです。

推論の最後に、大量のデータに対して、10ブロックまたは5ブロックのシングルショットKBでも十分に受け入れられる結果が得られるように予約したいと思います。このタスクでは、複数の10ブロッククロス検証を使用してモデルを構成します。

ランダムフォレスト

「ランダムフォレスト」は、受信したデータに対して多数の決定木をランダムに作成し、予測結果を平均化するアルゴリズムです。 ツリー構築アルゴリズムは非常に高速であるため、必要な数のツリーを簡単に作成できます。

実用的な観点から、上記の方法には1つの大きな利点があります。構成がほとんど不要です。 回帰であろうとニューラルネットワークであろうと、他の機械学習アルゴリズムを採用する場合、それらはすべて多くのパラメーターを持ち、特定のタスクに対して選択できる必要があります。 実際、RFには、設定が必要な重要なパラメータが1つだけあります。mtry（ツリー構築の各ステップで選択されるランダムサブセットのサイズ）です。 ただし、デフォルト値を使用しても、非常に受け入れられる結果を得ることができます。

前の記事のように、欠損値（N / A）をすべてのリグレッサの中央値に置き換え、サンプルからエンジンボリュームを除外し（パラメーターとパワーの強い相関関係により）、このアルゴリズムの機能を調べます。

dat <- read.csv("dataset.txt") #    R dat$mileage[is.na(dat$mileage)] <- median(na.omit(dat$mileage)) #  NA    dat <- dat[-c(1,11)] #         set.seed(1) #     ( ) split <- runif(dim(dat)[1]) > 0.2 #    train <- dat[split,] #      (cross-validation)  test <- dat[!split,] #  (hold-out)  

交差検証では、モデルの品質を評価するためのオプションがrfcvよりも多いキャレットパッケージを使用します 。

 library(caret) #   caret fit.control <- trainControl(method = "repeatedcv", number = 10, repeats = 10) train.rf.model <- train(price~., data=train, method="rf", trControl=fit.control , metric = "RMSE") #  10-  10-  -    train.rf.model #    - 

 library(randomForest) #   random forest train.rf.model <- randomForest(price ~ ., train,mtry=8) #        -  

モデルの各予測子の重要性を明確に示すグラフを作成します。

 varImpPlot(train.rf.model) #    

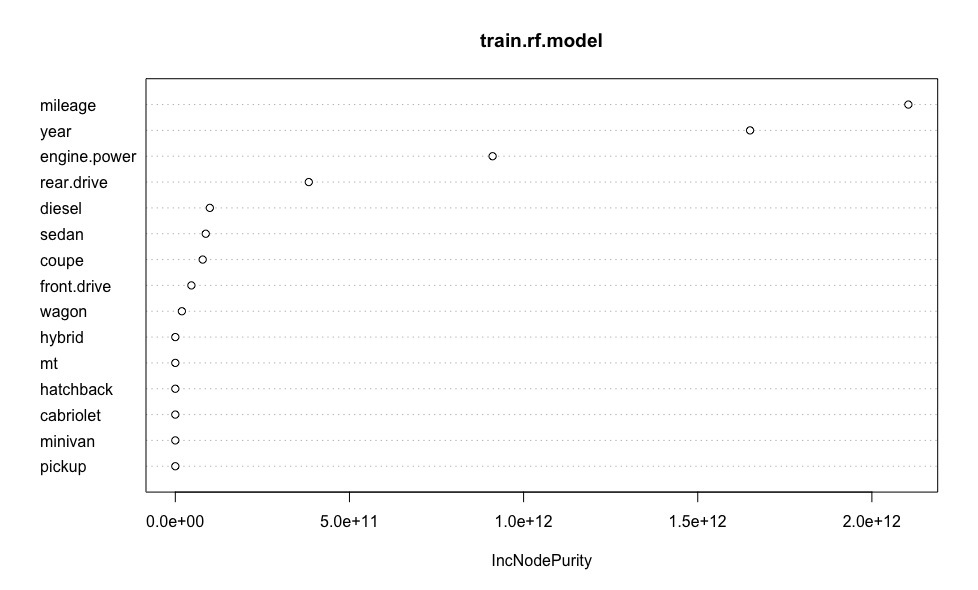
 rf.model.predictions <- predict(train.rf.model, test) #       print(sqrt(sum((as.vector(rf.model.predictions - test$price))^2)/length(rf.model.predictions))) #     ( ) [1] 121760.5 

車の値の推定で得られた平均誤差は、線形回帰で得られた同じ値と同等です。 RFとは異なり、線形モデルを構築する際に排出物を排除したため、自動車のコストを推定する際にさらに不正確になることに注意してください。 したがって、排出に対する 「ランダムフォレスト」の堅牢性について議論することができます。

Xgboost

勾配ブースティングのアイデアは、互いに順次改良する基本モデルのアンサンブルを構築することです。 後続の各基本モデルは、前の基本モデルからのアンサンブルの「間違い」についてトレーニングされ、モデルの応答は重み付けされて要約されます。

ほとんどすべてのモデル（一般線形、一般線形、決定木、K最近傍、その他多数）を「起動」できます。

xgboostのブースティングアルゴリズムの実装の機能には、まず、1次および2次導関数に加えて損失関数を使用することが含まれます。これにより、アルゴリズムの効率が向上します。 第二に、 再訓練に対抗するのに役立つ組み込みの正則化の存在。 そして最後に、カスタム損失関数と品質メトリックを定義する機能。

実験パラメータnum_parallel_treeのおかげで、同時に作成されるツリーの数を設定し、1回の反復でブースティングモデルの特殊なケースとしてランダムフォレストを提示できます。 また、複数の反復を使用すると、各「ランダムフォレスト」が基本モデルとして機能するときに、「ランダムフォレスト」のブーストが得られます。

記事の一部として、1つのタイプのブースト-xgbTreeのみを検討します。 xgbDartでも同様の結果が得られます。

 fit.control <- trainControl(method = "repeatedcv", number = 10, repeats = 10) train.xgb.model <- train(price ~., data = train, method = "xgbTree", trControl = fit.control, metric = "RMSE") #  10-  10-  - train.xgb.model #    - 

 library(xgboost) #   xgboost xgb_train <- xgb.DMatrix(as.matrix(train[-c(1)] ), label=train$price) #   xgb_test <- xgb.DMatrix(as.matrix(test[-c(1)]), label=test$price) #   xgb.param <- list(booster = "gbtree", max.depth = 1, eta = 0.3, gamma = 0, subsample = 0.5, colsample_bytree = 0.6, min_child_weight = 1, eval_metric = "rmse") train.xgb.model <- xgb.train(data = xgb_train, nrounds = 100, params = xgb.param) #        -  

モデルの各予測子の重要性を示すグラフを作成します。

 importance.frame <- xgb.importance(colnames(train[-c(1)]), model = train.xgb.model) #    library(Ckmeans.1d.dp) #    xgb.plot xgb.plot.importance(importance.frame) 

 xgb.model.predictions <- predict(train.xgb.model, xgb_test) #       print(sqrt(sum((as.vector(xgb.model.predictions - test$price))^2)/length(xgb.model.predictions))) #     ( ) [1] 118742.8 

この特定のケースのXGboostは、自動車のコストのわずかに正確な推定値を示しました。 車の選択されたメーカーとモデルに応じて、再構成を必要とする多数のハイパーパラメーターについて懸念があります。 この点で、 robasta.ruサービスで使用するには、ランダムフォレストアルゴリズムが優先されました。

選択したアルゴリズムのテスト

「チャンピオン」の選択が終わったので、今度は彼の行動を見てみましょう。

 library(randomForest) #   random forest rf.model <- randomForest(price ~ ., dat,mtry=8) #        -  predicted.price <- predict(rf.model, dat) #      real.price <- dat$price #        profit <- predicted.price - real.price #          

前の記事の線形回帰については 、価格に対する利益の依存関係のグラフを作成します。

 plot(real.price,profit) abline(0,0) 

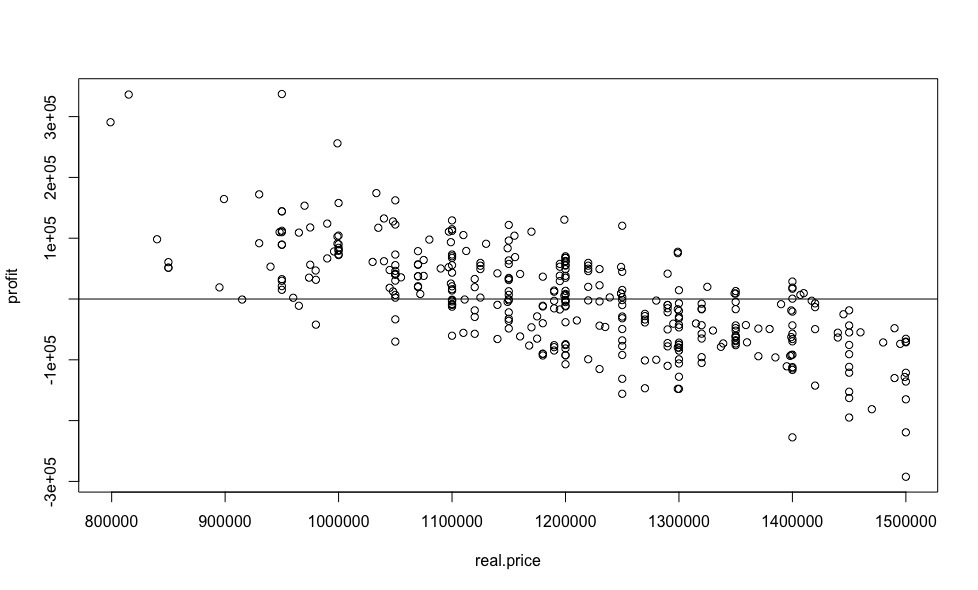
そして、利益の割合を計算しましょう。

 sorted <- sort(predicted.price /real.price, decreasing = TRUE) sorted[1:10] 69 42 122 15 168 248 346 109 231 244 1.412597 1.363876 1.354881 1.256323 1.185104 1.182895 1.168575 1.158208 1.157928 1.154557 

得られた結果は、線形回帰を使用して得られた結果と非常に弱く類似しており、両方のモデルの標準偏差がほぼ同一であるにもかかわらず、より妥当であるように見えます。

この記事の結果を比較するために、 以前の出版物のサンプルを使用したので、 メルセデス・ベンツEクラスが2010年より古くなく、現在市場に出ているモスクワで最大150万ルーブルの収益性の高いオファーの数を見てみましょう。



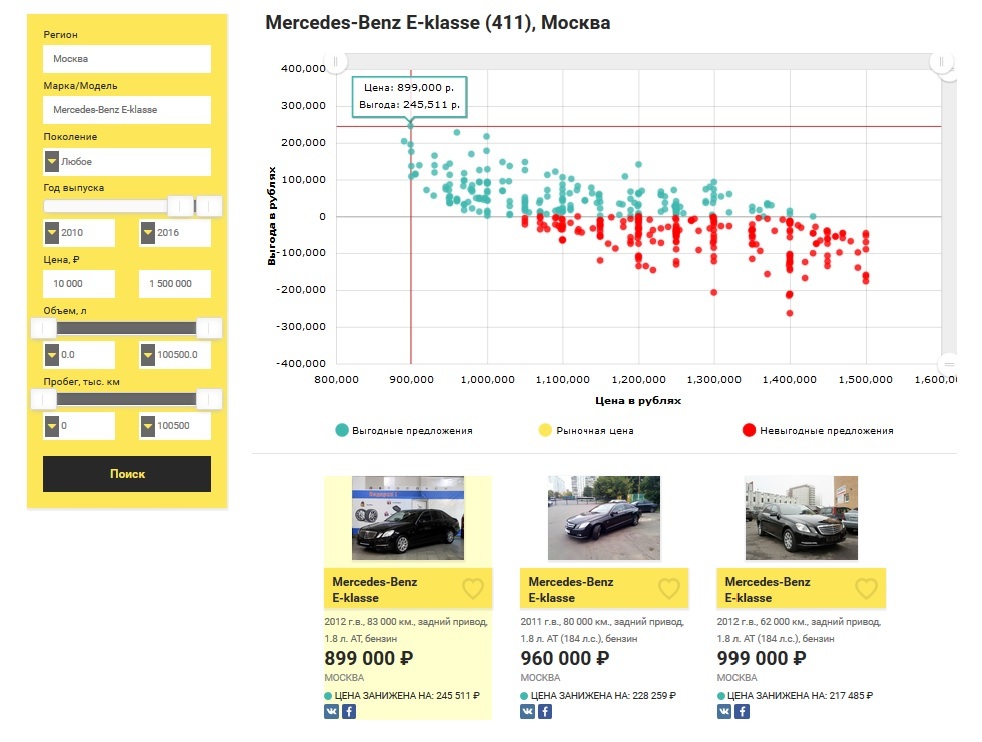
上記のすべてを要約すると、中古車の選択のために、「偽の」広告に敏感ではなく、リアルタイムで機能する強力なツールが得られたと自信を持って言えます。 車を販売する広告のあるいくつかのサイトに時間を費やす必要がなくなり、潜在的に不利益なオファーを見るために運転する必要がなくなります。

しかし、それだけではありません。現在、 ロバストは、考慮された数学的装置を使用して、購入したい人だけでなく、車を売りたい人も助けることができます。

車の販売

あなたの車を売るとき、あなたは、もちろん、少なくともそれを安くしないで、そしてそれを短時間で売りたいです。 あなたの車の迅速かつ有益な販売のためには、その価値へのさまざまな特性の貢献を理解する必要があります。

この問題を解決するために、同じ「ランダムフォレスト」に基づいて、自動車を評価するサービスが開発されました 。 車のパラメーターに従って、検索フォームのすべてのフィールドに入力します。その後、現在の市場のオファーに基づいてモデルがトレーニングされます。 市場に5つ以上の広告がある場合、入力するデータのアルゴリズムは価格を予測し、市場全体の状況に応じていくつかの興味深い機能を提供します。 最高の精度を達成するために、分析対象としてあなたと同じ世代の車のみが選択されることを強調する価値があります。 あなたの車の評価の結果はpdfレポートの形式で生成され、その費用は99₽です。

最後に

現在、さらなる開発のさまざまな方向性が検討されており、その中の主な方向性は次のとおりです。

比較的高価なTOの前に比較的新しい車（最大走行距離10万km）が販売されることがよくあります。これらのデータをモデルで考慮すると便利です。 したがって、現在、中規模および大規模の自動車ディーラーの信頼できるパートナーを探しています。

モスクワに車の選択と評価のためのオフラインセンターを開設します。これは、実装されたアルゴリズムのおかげで、競合他社よりもはるかに安価になります。

「インテリジェントリセラー」に機能を提供するための便利なAPIの作成。

私から発言されたタスクの実装に役立つものや、アイデアを提供したいものはありますか？ 書いて、私はいつでもどんな協力も検討する準備ができています。

参照資料

• dat （サンプルMB Eクラス）
• dat_a5 （Audi A5サンプル）