プログラミングと音楽：バターワース周波数フィルター。 パート3

みなさんこんにちは！ C＃でのVSTシンセサイザーの作成に関する記事の第3部を読んでいます。 前のパートでは、 VSTプラグインを作成するためのSDKとライブラリを検討し、信号振幅を制御するためのオシレーターとADSRエンベロープのプログラミングを検討しました。

このパートでは、シンセサイザーができない周波数フィルターの計算とコーディングの方法を説明します。 また、イコライザーがなければ、サウンド処理は考えられません。

ソースコードと、 NAudioライブラリ（.NETのサウンドを操作するためのライブラリ）のイコライザーの使用について検討します。

注意-多くのマタンがあります -フィルター係数の式を計算します。

私のシンセサイザーのソースコードはGitHubで入手できます 。

VSTイコライザープラグインFab Filter Pro Qのスクリーンショット

記事のサイクル

1. C＃WPFでVSTiシンセサイザーを理解して記述します
2. ADSR信号エンベロープ
3. バタワース周波数フィルター
4. 遅延、歪み、およびパラメーター変調

目次

1. イコライザー
2. フーリエ変換フィルタリング
3. デジタルフィルター
4. バターワースフィルターを使用する理由
5. LFフィルター式出力
6. ハイパスフィルターとバンドパスフィルターの式の導出
7. 得られた式に従ったバタワースフィルタープログラミング
8. NAudio Libraryのバンドイコライザー
9. フィルターを計算するためのプログラム
10. 参照資料

イコライザー

多くの場合、サウンドを処理するときは、そのキャラクター/色/音色を変更します。 音をより低音にしたり、高周波数を削除したり、その逆を行ったりして、音を「透明」にして、中央と上部のみを残します。 サウンド処理に携わっていない人の多くは、 イコライザーが何であるかを知っていると確信しています。スピーカー、ミュージックセンター、テープレコーダー、プレーヤーなどがあります。 イコライザーはフィルターのセットで、それぞれが選択した周波数帯域の信号の振幅を変更します。 家庭用スピーカーでは、これは通常2〜3個のノブです。低周波数、中音、上音、固定周波数帯域です。

Winampイコライザーには10個の定義済みバンドが既にあります。

Winamp Equalizerスクリーンショット

サウンド処理の世界では、あらゆる味と色に対応する多くのイコライザープラグインがあります。 Fab Filter Pro Qプラグイン（記事の冒頭のスクリーンショット）は、多数のバンドを作成してパラメーターを編集できるグラフィックイコライザーです。

イコライザーの各帯域は、実際には周波数フィルターです。 周波数フィルターは、信号の音色/周波数応答を変更します。 エレクトロニクスでは、多くの種類とフィルターの分類があり、対応する特性とパラメーターがあります- ウィキペディアを見てください 。
最も単純なフィルターであるローパス、ハイパス、バンドパスフィルターを検討し、プログラムします。

フーリエ変換フィルタリング

理論的には、信号を使用して離散フーリエ変換を行い、周波数を処理してから逆変換を行うことを気にする人はいません。

DFTの実装について考えない場合は、このアプローチを非常に直感的で簡単にプログラミングできると思います（ここでも、DFTを何らかの種類のものから自分でコーディングしない場合）。

アプローチの短所-最初に、DFTは、サイズが2のべき乗であるサンプルの配列から入力を受け取ります。 これは、出力信号がすでに遅延していることを意味します。 次に、512番目のサンプルごとに、DFT、信号周波数処理、逆DFTというアルゴリズムを作成します。 これらは小さな計算ではありません。 第三に、デジタル信号処理の支持者が知っている、まだ短所と微妙さがあります。

DFTの使用は考慮しませんが、デジタルフィルターの理論を見てみましょう。 サンプル値を処理し、入力サンプル配列の長さに応じて線形計算の複雑さを持つフィルターを作成しましょう。

デジタルフィルター

私は本のデジタル信号処理：実用的なアプローチからほとんどの情報と式の派生物を取りました-私はそれを強くお勧めします、それはロシア語版である- デジタル信号処理です。 実用的なアプローチ 、興味のある方はウェブ上でPDFを見つけるでしょう。

重要なポイントを述べたい。 フィルターの構築と計算のトピックは本当に非常に複雑で、多くの微妙さとニュアンスが含まれており、理論の知識と理解が必要です。 この記事では、読者がこれらの式の由来を理解できるように、バターワースフィルターの式を計算する方法を示します。 しかし、なぜそのような初期の式、なぜ正確にそのような置換が必要なのかは、デジタル信号処理の深層理論に突入することによってのみ理解できます。

フィルターコードをグーグルで調べ始めたとき、すぐに理解できない数学的コードをたくさん見つけたので、そのような計算式がどこから来たのかを少なくとも少し知りたいと思いました。 オシレーター、エンベロープ、遅延-これらのコンポーネントの動作を個人的に理解してプログラミングすることは、私には直感的ですが、フィルターではありません。 この記事では、デジタル信号処理への関心を喚起したいです）このトピックをより完全に理解したいという願望があれば嬉しいです。

畳み込み 、 フィルターのインパルス応答、フィルターの 伝達関数などの用語を（少なくとも少し）知る必要があります 。

理想的なフィルターの周波数応答の近似（ソビエトの教科書の写真、ソースが見つかりませんでした）

フィルターは信号を変更し、選択された周波数を「除去」します。 既存のフィルターは完全ではありません。 帯域幅-フィルターが「影響しない」周波数の帯域（一部あります 変更は、不完全なフィルターの機能です）。 抑制帯域-不要な周波数の帯域。 遷移帯域では、周波数の低下が発生します。 当然、フィルターは、通過帯域の歪みがどれだけ小さく、抑制帯域の周波数をどれだけ抑制し、遷移帯域がどれだけ狭いかによって、「理想的な」フィルターに近くなります。 フィルターにはさまざまな「近似」があります-チェビシェフ、バターボットフィルターなど-本やネットワークのオープンスペースにあります。

バターワースフィルターを使用する理由

すべてが非常に単純で、バタワースフィルターの周波数応答は通過帯域周波数で可能な限り滑らかです-私見、最も重要なことは、通過帯域の信号を損なうことではありません。

異なる次数のバターワースローパスフィルターの対数周波数応答（ウィキペディアからのスクリーンショット）

LFフィルター式出力

s平面上のバターワースフィルターの伝達関数は、次の式で記述されます。

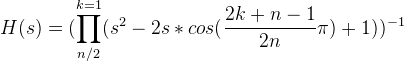偶数nと
奇数n

ここで、nはフィルターの次数です。カットオフ周波数wでの振幅は-3n dBであり、振幅周波数応答はオクターブごとに-6n dB減衰します。

たたみ込み係数を取得するには、次の形式でz平面の伝達関数を取得する必要があります。

2次フィルターの伝達関数（オクターブあたり-6 dBの減衰）を見つけ、H（s）n = 2の式に代入します。

次に、フィルターの畳み込みは次のようになります。

カットオフ周波数w（信号振幅が-3 dBになる）とFcにサンプリング周波数（1秒あたりのサンプル数）をヘルツ単位で与えてみましょう。

式では、非正規化周波数を使用する必要があります。 置き換えを行います（バンドパスフィルターには、通過帯域を決定する2つの周波数w1とw2があります）。

ローパスフィルターを計算する場合は、変換を行う必要があります。伝達関数のパラメーターsを置き換えます。

他のタイプのフィルター（ハイパス、バンドパス、ノッチ）を計算するには、他の置換を行う必要があります。 それらは、 デジタル信号処理の本で議論されています。 パート8.8.2以降の記事の実用的なアプローチ 。

次に、zプレーンに移動するには、変更を行います。

分析計算には、Mathematicaパッケージを使用しました。

zの多項式の形で分子と分母を取得する必要があります。 分母H（z）の項を共通分母に減らします。 これを行うには、分母項の最大公約数（GCD）を見つけ、元の関数H（z）の分子と分母をそれに分割します。

CoefficientList関数を使用して、結果の多項式のべき乗で係数を見つけます。

すべてが正直に行われた場合、条件により、a0は1に等しくなります-すべての係数をa0で除算します（コーディングでは、除算せずに前の式を使用します）。

ハイパスフィルターとバンドパスフィルターの式の導出

ハイパスフィルターの式の導出は、変換が異なるローパスフィルターに似ています。

バンドパスフィルターの式を導出するために、変換が適用されます。

置換を行うと、H（z）の分子と分母の多項式の次数が2倍になるため（置換にはs ^ 2があります）、フィルターの次数は2倍になります。 したがって、最初はn = 1に対して関数H（s）を使用します。

得られた式に従ったバタワースフィルタープログラミング

フィルターには、フィルタータイプ（ローパス、ハイパス、バンドパス）とカットオフ周波数wの2つのパラメーターがあります。 バンドパスフィルターでは、カットオフ周波数を通過帯域の中央の周波数と見なします。 通過帯域は、周波数間隔[w-w / 4、w + w / 4]として定義されます（ここで、より複雑で論理的な対数の法則を自由に選択できます）。

計算された式を使用して、係数b0、b1、b2、a1、a2（条件によってa0は1に等しい）を決定したとします。 フィルター操作アルゴリズムは畳み込みに縮小され、サンプルごとに順番に実行されます。

y（n）は、計算される新しいサンプル値です。 x（n）はサンプルの現在の値、y（n-1）とy（n-2）は前の2つの計算されたサンプル、x（n-1）とx（n-2）はサンプルの前の入力値です。

以前のサンプルの記憶を整理する必要があります。 循環バッファーでは賢くなく、単純で明確にする：3つの要素の2つの配列。 新しい値をこの配列に「プッシュ」するたびに、サンプルの古い値を順番にコピーします。

単純なクラスを取得します。

class BiquadConvolutionTable { public double B0, B1, B2, A1, A2; private readonly double[] _x = new double[3]; private readonly double[] _y = new double[3]; public double Process(double s) { // ""   _x[2] = _x[1]; _x[1] = _x[0]; _x[0] = s; _y[2] = _y[1]; _y[1] = _y[0]; //  _y[0] = B0 * _x[0] + B1 * _x[1] + B2 * _x[2] - A1 * _y[1] - A2 * _y[2]; return _y[0]; } } 

フィルターのワイヤーフレームクラスを記述しましょう（ 最初の記事のシンセサイザーアーキテクチャを参照 ）。 BiquadConvolutionTableクラスは、単一の信号で動作します。 1つのチャネルで-モノラル。 したがって、左右のチャネル用に2つのBiquadConvolutionTableが必要です。

フィルターを正しく適用するには、着信シーケンスのすべてのサンプルにBiquadConvolutionTable.Process関数を連続して適用し、結果のサンプル配列に入力する必要があります。

BiquadConvolutionTableの係数の計算は、関数CalculateCoefficientsによって実行されます。

 public enum EFilterPass { None, LowPass, HiPass, BandPass } public class ButterworthFilter : SyntageAudioProcessorComponentWithParameters<AudioProcessor>, IProcessor { private readonly BiquadConvolutionTable _tablel; private readonly BiquadConvolutionTable _tabler; public EnumParameter<EFilterPass> FilterType { get; private set; } public FrequencyParameter CutoffFrequency { get; private set; } public ButterworthFilter(AudioProcessor audioProcessor) : base(audioProcessor) { _tablel = new BiquadConvolutionTable(); _tabler = new BiquadConvolutionTable(); } public override IEnumerable<Parameter> CreateParameters(string parameterPrefix) { FilterType = new EnumParameter<EFilterPass>(parameterPrefix + "Pass", "Filter Type", "Filter", false); CutoffFrequency = new FrequencyParameter(parameterPrefix + "Cutoff", "Filter Cutoff Frequency", "Cutoff"); return new List<Parameter> {FilterType, CutoffFrequency}; } public void Process(IAudioStream stream) { if (FilterType.Value == EFilterPass.None) return; var count = Processor.CurrentStreamLenght; var lc = stream.Channels[0]; var rc = stream.Channels[1]; for (int i = 0; i < count; ++i) { var cutoff = CutoffFrequency.Value; CalculateCoefficients(cutoff); var ls = _tablel.Process(lc.Samples[i]); lc.Samples[i] = ls; var rs = _tabler.Process(rc.Samples[i]); rc.Samples[i] = rs; } } private void CalculateCoefficients(double cutoff) { ... } } 

関数CalculateCoefficientsはループ内で毎回呼び出されます-なぜですか？ 次の記事では、パラメーターの変調（時間の変化）について説明します。したがって、カットオフ周波数が変化する可能性があります。つまり、係数を再計算する必要があります。 もちろん、急いで、カットオフ周波数の変化にサブスクライブし、プロセッサに既にある係数を計算する必要があります。 しかし、これらの記事では最適化を扱いません。目標はフィルターをコーディングすることです。

係数の計算式に従って関数CalculateCoefficientsをコーディングします。
非正規化された周波数を使用する必要があることを思い出してください。 交換：

係数b0、b1、b2、a0、a1、a2のすべての式を書き留めます。 計算後、a0が1になるようにすべての係数をa0で除算する必要があります。

 private double TransformFrequency(double w) { return Math.Tan(Math.PI * w / Processor.SampleRate); } private void CalculateCoefficients(double cutoff) { double b0, b1, b2, a0, a1, a2; switch (FilterType.Value) { case EFilterPass.LowPass: { var w = TransformFrequency(cutoff); a0 = 1 + Math.Sqrt(2) * w + w * w; a1 = -2 + 2 * w * w; a2 = 1 - Math.Sqrt(2) * w + w * w; b0 = w * w; b1 = 2 * w * w; b2 = w * w; } break; case EFilterPass.HiPass: { var w = TransformFrequency(cutoff); a0 = 1 + Math.Sqrt(2) * w + w * w; a1 = -2 + 2 * w * w; a2 = 1 - Math.Sqrt(2) * w + w * w; b0 = 1; b1 = -2; b2 = 1; } break; case EFilterPass.BandPass: { var w = cutoff; var d = w / 4; //     [w * 3 / 4, w * 5 / 4] var w1 = Math.Max(w - d, CutoffFrequency.Min); var w2 = Math.Min(w + d, CutoffFrequency.Max); w1 = TransformFrequency(w1); w2 = TransformFrequency(w2); var w0Sqr = w2 * w1; // w0^2 var wd = w2 - w1; // W a0 = -1 - wd - w0Sqr; a1 = 2 - 2 * w0Sqr; a2 = -1 + wd - w0Sqr; b0 = -wd; b1 = 0; b2 = wd; } break; default: throw new ArgumentOutOfRangeException(); } _tablel.B0 = _tabler.B0 = b0 / a0; _tablel.B1 = _tabler.B1 = b1 / a0; _tablel.B2 = _tabler.B2 = b2 / a0; _tablel.A1 = _tabler.A1 = a1 / a0; _tablel.A2 = _tabler.A2 = a2 / a0; } 

 public enum EFilterPass { None, LowPass, HiPass, BandPass } public class ButterworthFilter : SyntageAudioProcessorComponentWithParameters<AudioProcessor>, IProcessor { private class BiquadConvolutionTable { public double B0, B1, B2, A1, A2; private readonly double[] _x = new double[3]; private readonly double[] _y = new double[3]; public double Process(double s) { // ""   _x[2] = _x[1]; _x[1] = _x[0]; _x[0] = s; _y[2] = _y[1]; _y[1] = _y[0]; //  _y[0] = B0 * _x[0] + B1 * _x[1] + B2 * _x[2] - A1 * _y[1] - A2 * _y[2]; return _y[0]; } } private readonly BiquadConvolutionTable _tablel; private readonly BiquadConvolutionTable _tabler; public EnumParameter<EFilterPass> FilterType { get; private set; } public FrequencyParameter CutoffFrequency { get; private set; } public ButterworthFilter(AudioProcessor audioProcessor) : base(audioProcessor) { _tablel = new BiquadConvolutionTable(); _tabler = new BiquadConvolutionTable(); } public override IEnumerable<Parameter> CreateParameters(string parameterPrefix) { FilterType = new EnumParameter<EFilterPass>(parameterPrefix + "Pass", "Filter Type", "Filter", false); CutoffFrequency = new FrequencyParameter(parameterPrefix + "Cutoff", "Filter Cutoff Frequency", "Cutoff"); return new List<Parameter> {FilterType, CutoffFrequency}; } public void Process(IAudioStream stream) { if (FilterType.Value == EFilterPass.None) return; var count = Processor.CurrentStreamLenght; var lc = stream.Channels[0]; var rc = stream.Channels[1]; for (int i = 0; i < count; ++i) { var cutoff = CutoffFrequency.Value; CalculateCoefficients(cutoff); var ls = _tablel.Process(lc.Samples[i]); lc.Samples[i] = ls; var rs = _tabler.Process(rc.Samples[i]); rc.Samples[i] = rs; } } private double TransformFrequency(double w) { return Math.Tan(Math.PI * w / Processor.SampleRate); } private void CalculateCoefficients(double cutoff) { double b0, b1, b2, a0, a1, a2; switch (FilterType.Value) { case EFilterPass.LowPass: { var w = TransformFrequency(cutoff); a0 = 1 + Math.Sqrt(2) * w + w * w; a1 = -2 + 2 * w * w; a2 = 1 - Math.Sqrt(2) * w + w * w; b0 = w * w; b1 = 2 * w * w; b2 = w * w; } break; case EFilterPass.HiPass: { var w = TransformFrequency(cutoff); a0 = 1 + Math.Sqrt(2) * w + w * w; a1 = -2 + 2 * w * w; a2 = 1 - Math.Sqrt(2) * w + w * w; b0 = 1; b1 = -2; b2 = 1; } break; case EFilterPass.BandPass: { var w = cutoff; var d = w / 4; //     [w * 3 / 4, w * 5 / 4] var w1 = Math.Max(w - d, CutoffFrequency.Min); var w2 = Math.Min(w + d, CutoffFrequency.Max); w1 = TransformFrequency(w1); w2 = TransformFrequency(w2); var w0Sqr = w2 * w1; // w0^2 var wd = w2 - w1; // W a0 = -1 - wd - w0Sqr; a1 = 2 - 2 * w0Sqr; a2 = -1 + wd - w0Sqr; b0 = -wd; b1 = 0; b2 = wd; } break; default: throw new ArgumentOutOfRangeException(); } _tablel.B0 = _tabler.B0 = b0 / a0; _tablel.B1 = _tabler.B1 = b1 / a0; _tablel.B2 = _tabler.B2 = b2 / a0; _tablel.A1 = _tabler.A1 = a1 / a0; _tablel.A2 = _tabler.A2 = a2 / a0; } } 

NAudio Libraryのバンドイコライザー

サウンド、.NETのさまざまな形式のサウンドファイルを操作するための優れたNAudioライブラリがあります。

これには、フィルタリング、 畳み込み 、 ゲート 、 エンベロープ 、 FFTなどの興味深い機能を備えたNAudio.Dsp名前空間が含まれています。

Equalizerクラス（例のNAudioWpfDemo.EqualizationDemo名前空間から）を考えてください。これにより、信号をイコライズできます。 このクラスはISampleProviderを実装します。ISampleProviderは、読み取り関数（float []バッファー、intオフセット、intカウント）でバッファーサンプルの配列を処理（変更）します。

コンストラクターは、イコライザーの「バンド」を記述するEqualizerBand構造体の配列を受け入れます。

 class EqualizerBand { public float Frequency { get; set; } public float Gain { get; set; } public float Bandwidth { get; set; } } 

ここで、Frequencyは、Qパラメーター（帯域幅、 フィルター品質係数 ）、ゲインGain dBを持つ帯域の中心周波数です。

実装を見ると、EqualizerBandの各バンドは、ピーキングフィルターとして使用されるBiQuadFilterクラスに対応しています。 すべてのフィルターは、連続して使用される信号を変更します。

EqualizerBandクラスはバターワースフィルターの実装であり、フィルタータイプとパラメーターの選択肢が豊富です。 実装を見ると、同様の式と係数を見ることができます。

Equalizerクラスの使用例は、EqualizationDemoViewModelクラスのNAudioWpfDemoプロジェクトにあります。

フィルターを計算するためのプログラム

デジタルフィルターの先駆者はアナログフィルターでした。 アナログ回路とアナログ信号処理の理論は、後にデジタル信号処理の理論に成長しました。

考慮されるバタワースフィルターと係数の計算式については、アナログ回路を組み立てることができます。

回路、それらの要素のパラメーター、さまざまなフィルターの畳み込み係数を計算および構築するための多くのプログラムがあります。
「フィルター計算ソフトウェア」でグーグル検索できます。

アイオワヒルズソフトウェアRFフィルターデザイナー

次の記事では、パラメータの遅延 、 歪み 、変調の効果について説明します。

すべてに良い！ プログラミングで頑張ってください！

参照資料

以前の記事の記事と本のリストを忘れずに見てください。

1. デジタル信号処理：実用的なアプローチ 。 ロシア語版- デジタル信号処理。 実用的なアプローチ 。
2. Habrの記事「フーリエ変換に関する簡単な言葉で」
3. Wikiのバターワースフィルター
4. バターワースフィルター計算コードを使用したGithubリポジトリ
5. 離散信号とシステム、第7章。FIRおよびIIRフィルター
6. ローパスフィルターはプログラムでどのように機能しますか？ （dsp.stackexchange.com/）
7. デジタルバターワースフィルターとチェビシェフフィルターの設計
8. オーディオEQクックブック
9. アイオワヒルズソフトウェア-デジタルおよびアナログフィルター