From:pratt@Sunburn.Stanford.EDU(ヴォーン・R・プラット)
ニュースグループ:comp.arch、comp.sys.intel
件名:FDIVバグの可能性が高い自然なシナリオ(だった:Intelの防衛で...)
日付:1994年12月3日15:20:17 GMT
組織:スタンフォード大学コンピュータサイエンス部。
行:194
メッセージID:<3bq2bh$ohc@Radon.Stanford.EDU>
参照:<3bdieq$lqf@engnews2.Eng.Sun.COM> <3bf666$6k4@hpsystem1.informatik.tu-muenchen.de> <3bnrgo$4gf@hermes.synopsys.com>
NNTP-Posting-Host:sunburn.stanford.edu
外部参照:Radon.Stanford.EDU comp.arch:15209 comp.sys.intel:20065
このメッセージでは、27,000年ごとに発生するIntelのデフォルトシナリオとは対照的に、3ミリ秒ごとに1回FDIVバグが発生するシナリオを示します。 さらに、遭遇したバグには不明瞭な数字は含まれていません。それらはすべて、5/15のような小さな「あざ」理論の形を取ります。 さらに、この例のように、発生するエラーのかなりの数が非常に大きくなります。 シナリオの妥当性は読者が判断できるようにします。 私の意図は、それが起こる可能性のあるものとして遭遇することです。
動機付け:記事<3bnrgo$4gf@hermes.synopsys.com>で、Joe Buckは次のように書いています。
>私はこの大騒ぎに本当に驚いています。 9件のうち1件
> 10億、本質的には単精度除算ではなく
>倍精度除算。 Pentiumユーザーの大多数は決してしません
>完全な単精度さえ必要とするもの:スプレッドシートを実行し、
>ドキュメントを作成し、ゲームをプレイします。 インテルが約10億を支払うべき理由
>(これは9個のゼロです)これらのすべてのルアーに新しいチップを搭載するためのドルですか?
90億分の1、ない。 ユーザーのプログラムで発生する実数が均一に分布することはよくある誤りです。 それらの実際の分布は、以下で説明するシナリオのように、プログラムがそのデータを取得する場所とそれが何を行うかに大きく依存します。
NOT単精度内に修正します。 もちろん、16ビットの語長を念頭に置いていない限り、 〜16ビットエラーの他の例は既に提供されていますが、上記の4.999999 / 14.999999のようなここでのエラーの形式は、特に劇的です。
このメッセージでは、数論、暗号、微分方程式、または行列の反転を伴わず、プロセスによってわずかに「ゆるめ」られた実数として表される1〜3桁の整数による単純な除算を含む、単純でもっともらしいシナリオを示します。私たち全員が何度も見ています。 このシナリオでは、FDIVバグは、27,000年ごとに1回ではなく、3ミリ秒ごとに1回、Pentiumがそれらに遭遇した割合を明らかにします。
ここでの重要な仮定は、このシナリオで遭遇する整数は、他の処理のために非常にわずかに「ゆるめ」られ、その後、何らかの理由で(たとえば、数値は10進計算機から自動的に取得される可能性がある)、いくつかの事前に決められた数に切り捨てられることです10進数、*精度*。 すべての整数は、固定された精度のために、この処理に対して一様に条件付けられます。 したがって、精度が6で、7を18で割ると、7は実際には6.999999で、18は17.999999です。つまり、同じ量(ここでは10 ^ -6)が両方のオペランドから減算されます。
1 <= i、j <= 1000の整数i、jのペアが100万個あります。次の表は、10進精度の低下と*許容度*(除算からの距離)間違った答えとしてカウントします)、100万の部門i / jのうちどれだけが間違っているかを調べます。 これらの商については、IEEE正解は10 ^ -17を超える相対誤差を持つと予想されます。 次の表では、「間違った」と定義して、相対誤差が最初の列で少なくとも10 ^ -15、2番目の列で少なくとも10 ^ -13などであると定義しています。 (つまり、テーブルを横切っていくとうるさくなり、商が間違っていると認識する回数が少なくなります。)
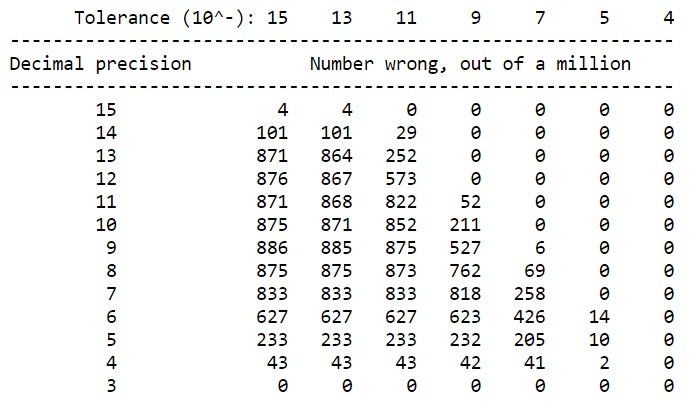
精度が6桁の場合、切り捨て誤差は100万分の1で、簡単に覚えられる量です。 この場合、カクテルパーティーでの制作の場合のみ、読者は最悪の犯罪者のうちの2人または3人を記憶したいと思うかもしれません。
私のお気に入りは5/15、つまり4.999999 / 14.999999で、他の鑑定士がより公正な答えとして0.33333329を要求するときに0.33332922でPentiumによって評価されます。
もう1つの悪いケースは7/48(6.999999 / 47.999999)です。これは、より刺激的な推測が0.14583332である場合に、Pentiumが0.14583204を推測します。
もう1つの候補:9/54(8.999999 / 53.999999)、ペンティアムは0.16666439でギャンブルし、0.16666665にペナルティを失います。
これらの例の3つの本質的な特徴を強調します。 第1に、基本的な算術演算は非常に小さな整数(わずかに「打たれた」)であるため、これらの正確なエラーに気付くかどうかにかかわらず、発生する可能性が大幅に高まります。 第二に、あざは100万分の1や1000万分の1などの単純な量である可能性があり、0.000000142883のようなあいまいな量である必要はなく、状況で発生するあざがあなたにとって悪い可能性が大幅に増加します。 第三に、エラーはFDIVの両方のオペランドに均一に適用できるため、オペランドのエラーを個別に調整する必要がないため、これらのエラーのいずれかが発生する可能性がさらに高くなります。
これらの3つの例の奇妙な特徴は、時間が経てば私が追求しておらず、統一された説明を持っているかもしれないし、持っていないかもしれないことです上記の^^で。 これにより、次の3つの例でPentiumをエミュレートするための単純なヒューリスティックが得られます。ポケットカルキュレーターで4.999999 / 14.999999などを計算し、2桁の繰り返し数字を削除します。 結果は、繰り返し文字列を超えて1桁(5/15の場合は実際には2桁)になります。
これら3つの例の相対誤差は、精度よりも大幅に大きいことに注意してください。
許容差10 ^ -5で生き残るのは26ペアのみです。 記録の精度6の14の間違ったもの:5 / 15、5 / 30、5 / 60、5 / 120、9 / 54、9 / 108、9 / 216、9 / 432、9 / 864、 10 / 60、10 / 120、10 / 240、10 / 480、および10/960。 (7/48は0.9 * 10 ^ -5だけオフになっています。許容誤差10 ^ -5をほとんど逃していません。)精度5の場合、10人の悪者は18 / 27、20 / 30、33 / 144、36 / 108です。 、40 / 120、44 / 192、72 / 432、72 / 864、80 / 480、および80/960。 精度4の場合、2つの区分は82/96と120/288です。 具体的には、81.9999 / 95.9999は0.8541665を期待したときに0.854156を返し、119.9999 / 287.9999は0.416656を返し、0.4166665が必要でした。 (うーん、delete-two-repeatsルールはここでも機能します;非常に興味深い...)
精度の概念として基数10を想定していましたが、特別なものではなく、他の基数も同様の結果をもたらすはずです。 特に、10本ではなく13本の指を進化させた場合、許容範囲10 ^ -9で11桁から3桁に対応するテーブルは、0、31、211、547、802、784、417、109、0になります。
このシナリオでは、少なくとも私にはかなり悪い光のように見えるものにFDIVのバグが入りますが、最悪のシナリオのようなものではないと主張します。 シナリオの2つの重要な要素は、そのシナリオがFDIVバグをトリガーするレートと、そのシナリオの本質が実際にどのくらいの頻度で発生するかです。 シナリオの「損傷指数」は、これら2つの要因の積です。 実際のPentium時間の数千時間を占めるが、10分ごとにバグをトリガーするだけのシナリオは、上記のシナリオよりも高いダメージインデックスを持っている可能性があり、その強さは数ミリ秒ごとにバグをトリガーするが、その弱点はそれが実際に実際にどれほどありそうかについての不確実性。 ただし、これは完全に信じがたいシナリオではないことを認めなければなりません。
-ooooooooooooooooooooooo-ooooooooooo
ここに、上記の表を印刷するコードを追加します。 Cで調和しないと思う人にとっては、これが「精度」と「許容」の正確な意味を探す場所です。
#include #include main(argc, argv) char *argv[]; { int i, j, cnt, digits; double prec, tol, ibruis, jbruis, pent, true; for (digits = 15, prec = 1e-15; digits > 2; digits--, prec *= 10) { printf("%4.d\t\t", digits); for (tol = 1e-15; tol < 1e-4; tol *= 100) { cnt = 0; for (i = 1; i <= 1000; i++) for (j = 1; j <= 1000; j++) { ibruis = i - prec, jbruis = j - prec; pent = ibruis/jbruis; true = (1.11*ibruis)/(1.11*jbruis); cnt += (fabs(pent - true) > tol*true); } printf("%4d ", cnt); } printf("\n"); } }
真の商、つまりtrue =(1.11 * ibruis)/(1.11 * jbruis)を取得するためのヒューリスティックは、FDIVバグをヒットする確率を少なくともある程度インテルに近づけるのに十分なだけオペランドをランダム化する迅速で汚れたものです27,000年に1回の推定。 1.11を1.01に置き換えたとき、結果は同じであり、Intelの見積もりと合わせて、飛行機の建設を目的としないプログラムには十分であると思われました。
ヴォーン・プラット
[
ソース ]