はじめに
wufoo.comの再設計と改訂に
備えて 、私は人間とコンピューターの相互作用の基本を再検討し、数十年にわたって蓄積された新しいものを組み込み、シンプルなインターフェースを作成することを望んでいました。 途中で私を驚かせた最初のことは、このトピックに関する資料が非常に簡潔であり、数学のエリートの言語で書かれたように数学者に明確に向けられていたことでした。 彼ら(特にデザイナー)に感銘を与えたいなら、彼らは理解しやすい文書を書くことができると仮定することができます。
学校を思い出して、私は物理学の研究中にのみ、数学が私にとって何らかの意味を獲得したことに気付きました。 抽象的な機能の代わりに、グラフィックが必要でした。 このように考えて、ヒューマンマシンインターフェイスの設計の基礎であるフィッツの法則を明確に解釈し、その概念と、これらのアイデアが多くの人が望むよりも少し複雑である理由の両方を説明するのが良いと思いました
明らかな数学
1954年に公開されたフィッツの法則は、インターフェイスを開発するときに発生する特定の、非常に一般的な状況をモデル化するための効果的な方法です。 この状況には、人(指の形の物理的なもの、またはマウスカーソルのような仮想的なもの)によって制御されるオブジェクトと、別の場所にあるターゲットが含まれます。 この状況は、最初の図に示されています。

数学的には、フィッツの法則は次のように記述できます。
T = a + b log2(D / W + 1)、
ここで、Tはアクションを完了するのにかかる平均時間、aはデバイスの開始/停止時間、bはデバイスの一般的な速度に応じた値、Dは開始点からオブジェクトの中心までの距離、Wはオブジェクトの幅で、移動軸に沿って測定されます
これは主に、目標に到達するのにかかる時間が、目標の距離とサイズの関数であることを意味します。 一見したところ、これは明らかなようです。ターゲットから遠ざかるほど、サイズが小さくなるほど、配置にかかる時間が長くなります。 トム・スタッフォードはこのアイデアを開発します。
「メインメッセージは明らかですが(大きなものを選択する方が簡単です)、対数関数が含まれているため、正確な数学的特性は印象的です。つまり、サイズと反応時間の関係により、小さなオブジェクトのサイズが少し大きくなると区別しやすくなります(一方、大きなオブジェクトの小さなサイズ変更は問題ではありません)。 ゴールまでの距離についても同じことが言えます。」
現実の世界に目を向けると、そばかすよりもコインを指す方がはるかに簡単ですが、家や住宅の複合体を示すことはほとんど違いがありません。 したがって、フィッツの法則に従ってWebサイトを再度最適化する場合、リンクがすでにかなり大きい場合、リンクをさらに増やしてもアクセス速度は向上しないことに注意してください。 ただし、小さなリンクのサイズのわずかな増加でさえすでに重要です。
フィッツの法則は線に適用されます!
フィッツの方程式から実用的なレッスンを学びたいと思って、インターフェイス設計者は、人間とコンピューターの相互作用の数少ない法則の1つを実際に適用するためのいくつかのルールを推測しました。 ルールの1つが呼び出されます
目標サイズのルール
フィッツの法則とヒックの法則(これについては後で説明します)を導くアイデアを、ボタンのサイズはその使用頻度に比例させるべきであるというステートメントに結合します。 Appleのインターフェースの第一人者であるBruce Tognazziniは、オペレーティングシステムのインターフェースを大幅に改善するルールを開発するためにFittsの法則をどのように使用できるかを説明する優れた
クイズを開発しました。
これらのルールをアプリケーションに盲目的に適用する前に、フィッツの法則が非常に特定の状況を説明していることを思い出してください。 これは、開始点からの動きが明確で方向性があるという仮定に基づいています。これは、厳密に定義された直接的な軌道を意味します(他のターゲットが存在しないかのように、高い初期速度で開始し、必要な場所を正確に知っていました)。 また、多くの人がフィッツの法則が以下の状況を説明していると考えていることを見ました。

ただし、上記の式では、ターゲットの高さに対応する値はなく、幅のみが含まれます! したがって、インターフェイスに関するフィッツの法則の制限について話し始めたので、一次元の状況を説明していると言えます。 フィッツの最初の実験では、ターゲットに向かって水平方向の動きを行う際の人間のパフォーマンスが研究されました。 運動の振幅と最終領域の幅の両方が同じ軸に沿って測定されたため、法則を記述するモデルは次のようになります。

したがって、フィッツの法則に従ってサイズ最適化を構築する場合、垂直および斜めの動きは同じ方程式で記述されると想定できます。 実際、別の目標を指すことができる容易さは、実際には、開始点と目標の相対的な位置に依存することがわかります。
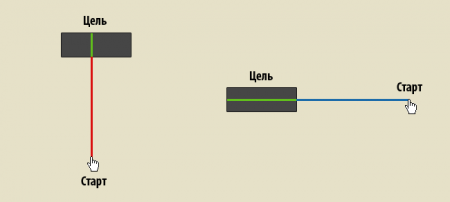
上記の例では、幅が広いため、右側のカーソルは、左側の状況よりも技術的にはターゲットをヒットするのに有利な状況にあります。 中心までの距離はどの角度でも同じであるため、フィッツの法則は丸い目的でもうまく機能することに注意してください。 ただし、長方形で複雑なオブジェクトの場合、法則の精度は低下します。 次の例では、四角形のサイズを大きくして、リンク領域を最適化するために2回試行します。
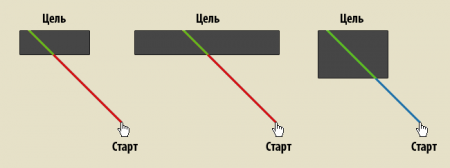
前者の場合、ターゲットの長方形の幅を増やし、2番目の場合、高さを増やしました。 ご覧のとおり、この開始点では、すべてのサイズの増加がターゲットへのより簡単なヒットという形で影響を与えるわけではありません。これは、CSSおよびBoxモデルを使用して作業するWebデザイナーにとって重要です。
物理的および仮想的なポジショニング
フィッツの研究の発表以来、数百の派生実験が行われてきました。 1996年にEvan GrahamとChristine Mackenzieによって1つの興味深い研究が行われ、実世界と仮想世界でのオブジェクトの配置の違いが分析されました。 開始点からターゲット領域への移動は、初期高速フェーズと減速フェーズの2つの部分に分割できることを示しています。

この研究では、著者らは、第一段階は主に標的までの距離によって影響を受けると結論付けました。 画像の縮尺もオブジェクトのサイズもターゲットへのアプローチを加速しません(サイズが大きいリンクでも移動速度は上がりません)。 等しい距離にある小さなオブジェクトを選択するのにかかる時間に影響する唯一のフェーズは、減速フェーズです。 そして今、興味深いこと:
「仮想ディスプレイと物理ディスプレイの違いは、小さなターゲットへの減速の視覚的制御が物理的タスクよりも時間がかかる仮想タスクである場合に、動きの第2フェーズでのみ明らかです。」
簡単に言えば、マウスではなく指で画面上のリンクやボタンをクリックする方が簡単です。 また、マウスの問題は、ターゲットにヒットする能力ではなく、確実にスローダウンする能力にあります。 Apple、マルチタッチ対応のモニターはすべて希望です。
無限境界ルール
コンピューターモニターには、エッジと呼ばれるものがあるため、Fittsターゲティングモデルの非常に興味深い副作用が発生します。 The Horror of Codingの著者であるJeff Atwoodは、昨年の記事であるFitts 'Law and the Infinite Widthでそれをほぼ完璧に説明しました。
ポインティングデバイスは任意の方向に任意に移動できるため、画面の端にあるターゲットは、以下に示すように実際には無限の幅を持つターゲットです。
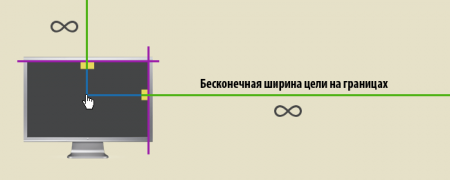
オペレーティングシステムとすべてのフルスクリーンアプリケーションの場合、技術的に最もアクセスしやすいため、これらの境界は通常、最も貴重な場所と見なされます。 無限の幅があるだけでなく、到達したときにユーザーがブレーキをかける必要がないためです。 そのため、ウィンドウ間をナビゲートするなどのアクションを画面の隅に割り当てるのは非常に簡単で直感的です(Compiz Fusionで行われているように-
約 )
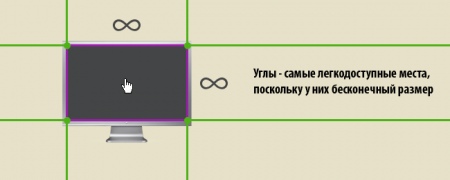
残念ながら、Webアプリケーションには、無限の境界のルールの利点がありません。 境界線のあるブラウザウィンドウで起動する必要があるという制限があるため、ブラウザがフルスクリーンモードで起動されない限り、エッジとコーナーに沿ったボタンとリンクの位置は特に関心がありません。 。

これは、Webベースのオペレーティングシステムのインターフェイスが、モニター領域全体を利用するインターフェイスほど優れたものにならない理由も説明しています。
Fittsはまだ操縦します!
前述のフィッツの法則の制限のいくつかは、彼を窓から追い出す理由にはまったくなりません。 私は彼の周りの議論が50年前のように今日まで落ち着いていないことを示したかっただけです。 そして、彼はインターフェイスの分野のほとんどの状況を技術的に正確に説明することができないため、人々は常に自信を持って目標に向かって移動するわけではなく、直接的な経路を使用せず、通常、混乱を招く可能性のあるいくつかの目標があります-より正確ではないようです他の多くの要因を考慮に入れたモデルは、フィッツの法則の根底にある基本的な真実を変える可能性があります。
「フィッツの法則は、さまざまな手足(腕、脚、視線検出器)、マニピュレーター、物理的環境(水中を含む)、ユーザーグループ(若い、古い、反応が遅く、薬物の影響下にある人も含む)を含む多くの場合に適用できることが示されています」
結論として、設計者に伝えたい主なアイデアは、アプリケーション設計の開発タスクが非常に複雑で豊富であり、フィッツの法則の包括的な適用に注意する必要がある非常に多くの変数が含まれているということです。 モニターのサイズの増加、マウスアクセラレーションの増加方法の人気の高まり、および大画面でのスクロールテクノロジーにより、ソフトウェア開発者がこれを利用して長距離をすばやく克服する能力を向上させる方法を見るのは興味深いでしょう。