どういうわけか私は長い間何かを書きたかったのですが、それはすでに起こりました。 そして、機会はそれ自体を提示し、さらにそう、インターネットはすぐに何も与えませんでした...
教えられたコースについてA. Dainiakに大いに感謝したいと思います。これはコースの要約に過ぎず、それ以上のふりはしないと付け加えます。記事ツリー全体=二分木小さな木（5-10など）のシートを描くのは本当に簡単です。 そして、それらのために、自然な表現
（LKPタイプのもの）を使用できます。 そして、それはかなり良いことが判明しました。
たぶん、100個のノードのツリーを描画することもできます。 しかし、さらにノードがある場合-たとえば、1000、あなたは木を描くことができます。 しかし、それらを読むこと（および理解すること）は非常に不便です。 さらに、読むことによって、画面上の木の画像を正確に意味し、それらが単に無期限に塗りつぶされないようにします。 一つの大きなスポットに。
これに対処するためのオプションの1つですが、おそらく
多くの苦労は
ありませんが、通常の視覚化のある種の構造-
水平 垂直 ツリーです。 つまり、これは視覚化に使用されます。
- でのみ歩く
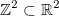。 ただし、これは実装に関しては完全にオプションです。 それは私たちにとって便利です。 - 面積と読みやすさの点で何らかの形で成功を収めたいと考えています。 （しかし、今はそれについて話したくありません。それは、非常に狭くて長い木片がまったく読めないと言うことができるだけです。）
だから-HVツリーを表す概念は単純（そして再帰的）です。ツリー1とツリー2があり、それらを結合したい場合（つまり、同じツリーのサブツリーを作成した場合、この操作は行われます）：
つまり、接着が完全に正式に行われる方法：
1.与えられたエッジの長さを持っています（一般的には自然です）。 そして、私たちはどのようなルールに従って一緒に固執できます。 私たちがすること：
ルート、S = 0に到達します。 ルートからすべてのシートに移動し、右（画面から）に移動するたびにS = S + 1になります。
2. 2番目のツリーでも同じです。
3.幅の広い（Sが多い）ツリーを修正します。 そして、右側が残りです。
それらが等しい場合、どのようにハングアップするかは重要ではありません（もちろん、どうにかして写真を制限したい場合は、ずっと長くした方が良いでしょうが、プレゼンテーションに制限がない場合は、反対にしようとする価値があります-見る方が便利です）
これがまさにそのようなツリーとプロセスと構造を定義する方法です。
さて、例として-標準形式とハードウェア敷設の表現の比較。
- stdの不完全なツリー。 提出。
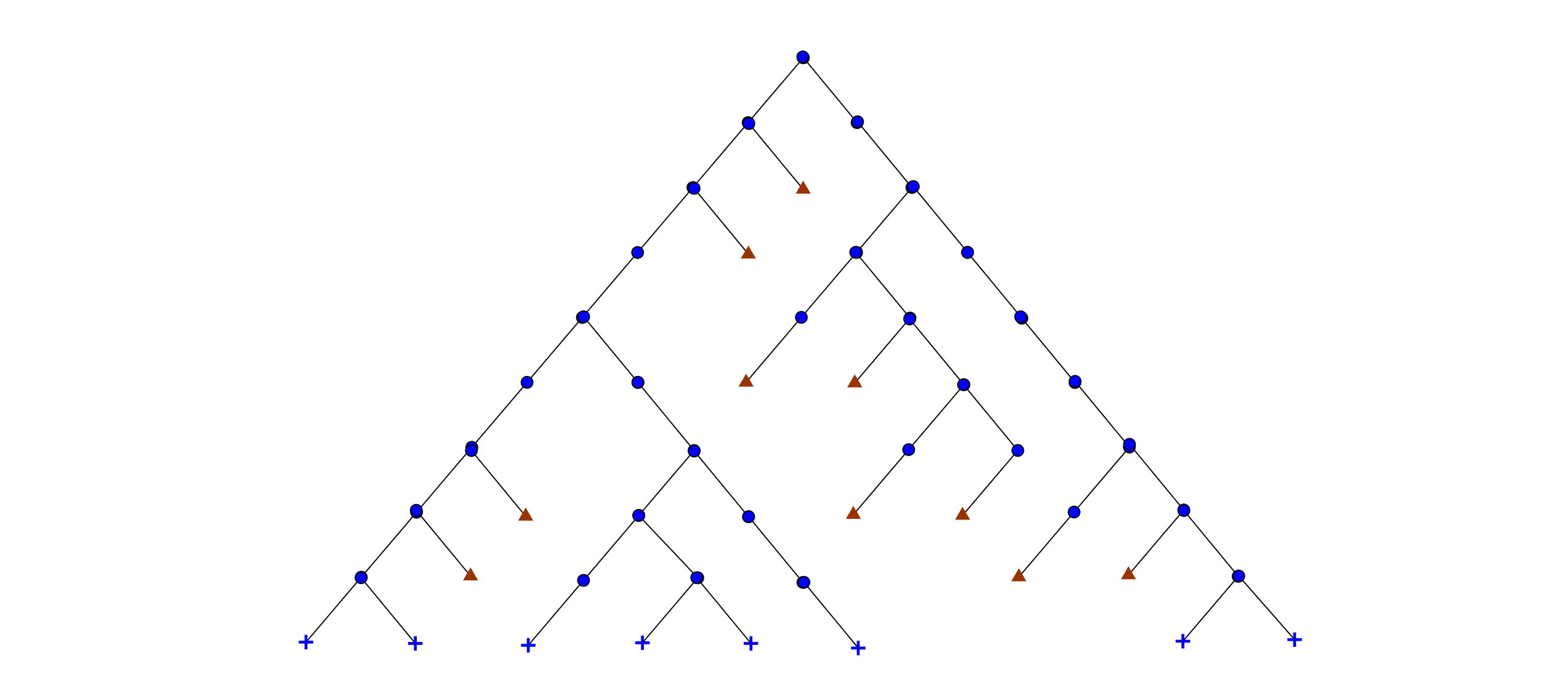
- 標準のフルツリー。 パフォーマンス：同じ幅のリブを持つツリー全体を想像することはできません。 （むしろ、エッジが下位レベルn（シートはレベル0、プレリストは1）のノードから出ている場合、エッジの長さはn * sである必要があります（sはユニットエッジです）（私の図面では、これはすぐではありません。エッジのコーナーを移動したこと。）
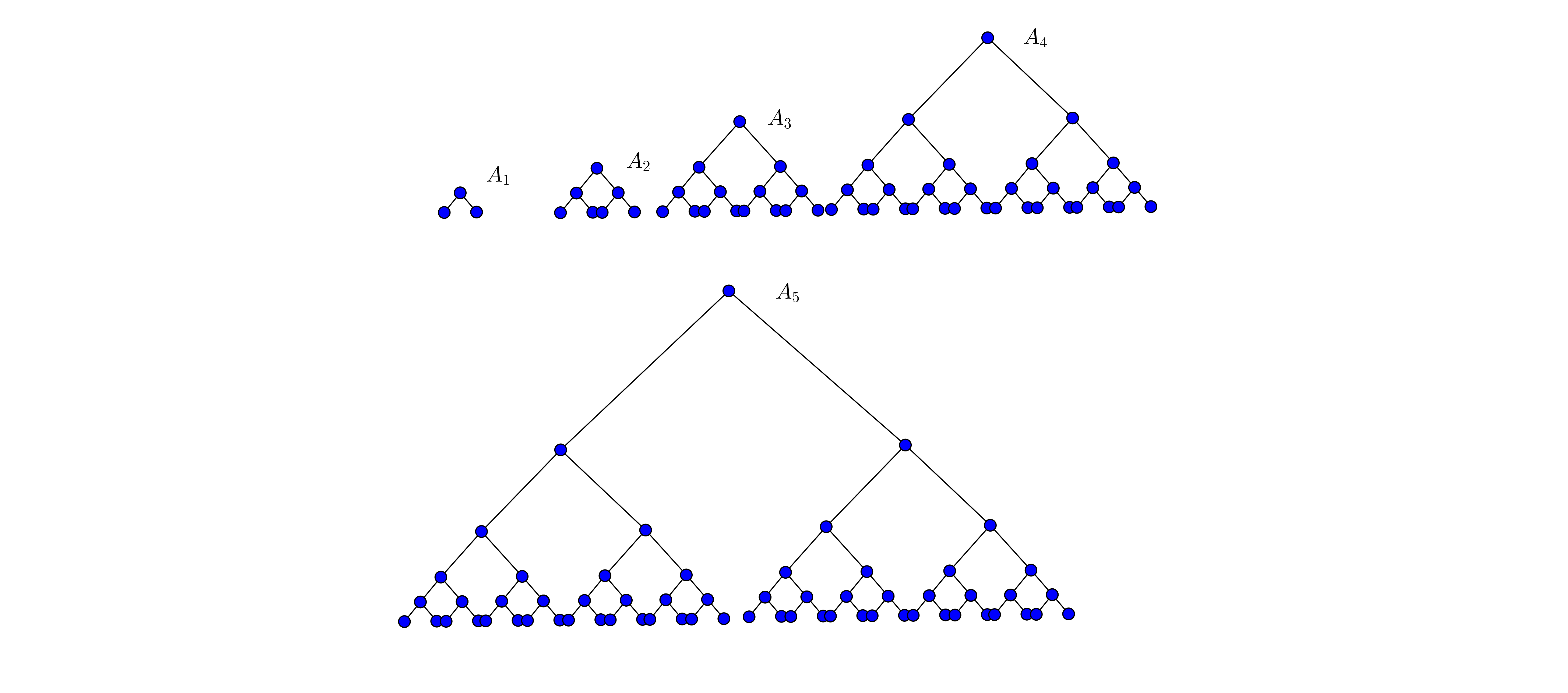
- HV表現の最初のツリー。 これは、最初の図と同じツリーです。
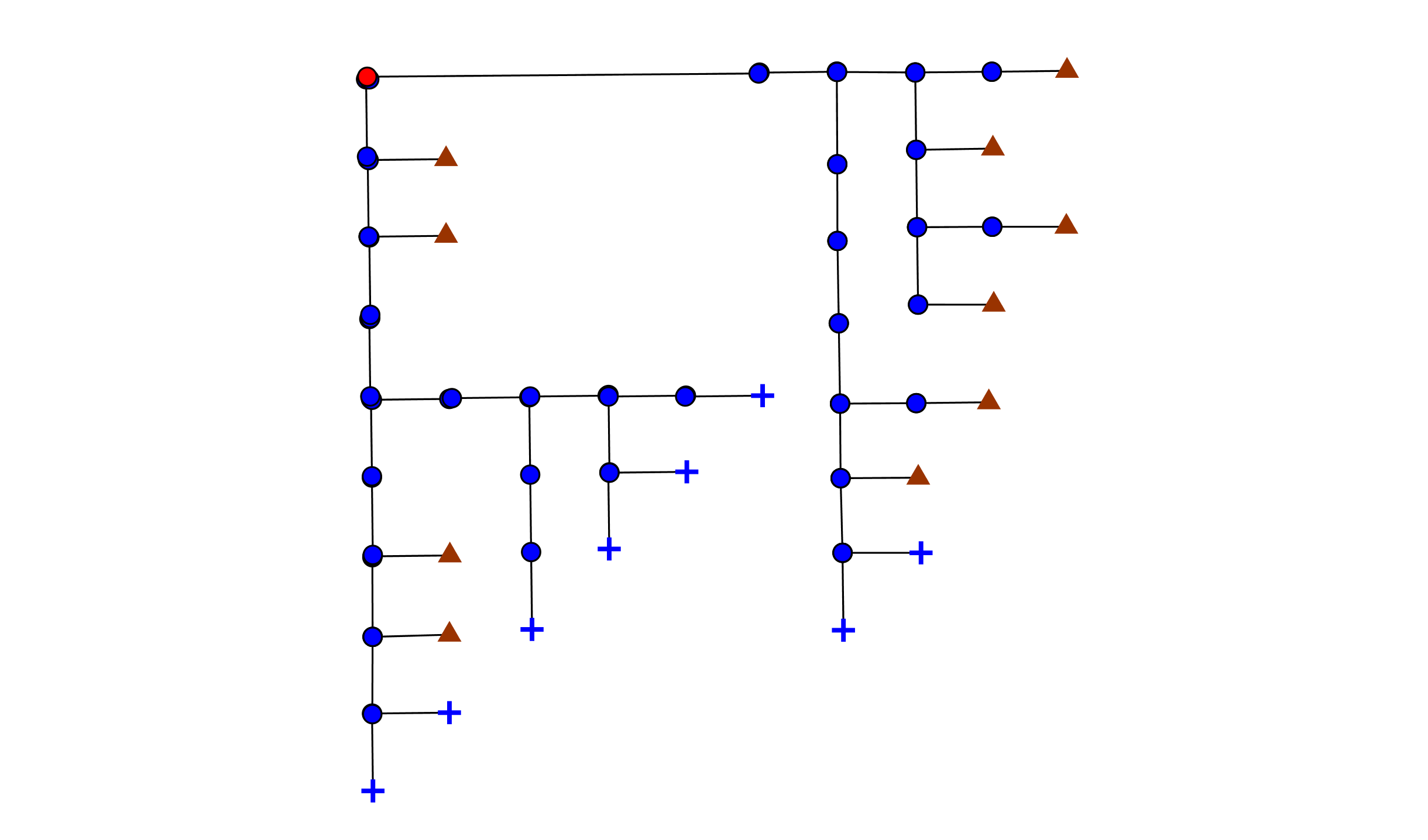
こっち このようなパフォーマンスは、原則として標準のプレゼンテーションよりも多少優れています。