
ニューラルネットワークは現在、傾向にあります。 私たちは毎日、彼らがインターネット上でコメントを書き、市場で交渉し、写真を処理する方法を学んでいます。 リストは無限です。 これを動かしているコードの規模を最初に見たとき、私は怖くてこれらのソースを見たくありませんでした。
しかし、私の生まれつきの好奇心と熱意は、GitHubに3k +スターを備えたJSでニューラルネットワークを構築するためのフレームワークプロジェクトであるSynapticの開発者の1人になるまでに至りました。 現在、このフレームワークの作成者は、GPUおよびWebWorkerで高速化し、適切なNNフレームワークのほぼすべての主要機能をサポートするSynaptic 2.0を作成しています。
その結果、ニューラルネットワークは難しくなく、かなり簡単な原理で動作し、理解および再現が容易であることがわかりました。 最も難しいタスクはトレーニングですが、そのためにほとんど常に既製のアルゴリズムを使用し、それらをコピーすることはそれほど難しくありません。
それを証明するのは簡単です。 以下の記事では、ライブラリなしでゼロからニューラルネットワークを実装します。
手始めに-少しの背景。
10月末に、サンクトペテルブルクで開催された#ITsubbotnikイベントでプレゼンテーションを行い、ここで続けることにしたトピックを開始しました。 JavaScriptでニューラルネットワークをゼロから作成する方法について説明しましょう。
あなたが私のスピーチの最初の部分にいたか、またはyoutubeでそれを見たなら、あなたは次のいくつかのパラグラフをスキップすることができます-これはそれの簡単な言い直しです。
ニューラルネットワークとは
会議で経験豊富な一人から最高の定義を聞きました。 彼は、ニューラルネットワークが思いついた美しい名前だと言いました。なぜなら、「行列の操作の連鎖」を定義するための許可を得るのははるかに難しいからです。
一般に、これはニューラルネットワークの実際の状況を非常に正確に表します。 これはクールで強力な技術ですが、実際の情報よりも誇張されています。 「ニューラルネットワークが暗号化アルゴリズムを発明した」などのことを行う同じGoogle Brainは、テーマコミュニティで一貫して笑されています。会社。
ネットワークが何であるかを説明するには、遠くから少し行く必要があります。
データサイエンティストの観点から(たとえば、神経科学者の観点はまだあります)、ニューラルネットワークは、何らかの物理プロセスをモデル化するためのツールの1つです。 また、モデリングツールは次のように機能します。
- かなりの数の観察を行います
- これらの各観測の重要な情報を収集します
- この情報から知識を得ます
- この知識を通じて解決策を見つけます
線形関係
例として、冶金学を取り上げることができます。 2つの金属の合金があると想像してください。 たとえば、80%の鋳鉄と20%のアルミニウムを使用する場合、1トンの鉄を押し付けると、そのような合金の梁が破損します。 70%+ 30%を使用すると、2トンを押すと破損します。 60%+ 40%-3トン。
オプション50%+ 50%は4トンに耐えるものと想定できます。 人生では、すべてが少し異なって機能しますが、単純化されます-それがそのように機能すると想像できます。
実際には、これは通常、膨大な数の観測値がすでにそこにあるという事実につながり、それらに基づいて、たとえば、そのような答えを与える何らかの種類の数学モデルを構築できます。
最も単純で効果的なツールの1つは、線形回帰です。 上の例-合金の%は最大荷重に直接比例します-は線形回帰です。
一般に、線形回帰は次のとおりです。
function predict(x1, x2, x3..., xN) { return weights.x1 * x1 + weights.x2 * x2 + ... + weights.xN * xN + weights.bias; }
用語「重量」、重量を覚えておく価値があります。 さらなる例では、それも使用されます。 各パラメーターの重み(または重要度)は、予測モデルにおけるその重要度です-ニューラルネットワークと線形回帰の両方が、予測のためのモデルの本質です。
「バイアス」の重み、または「シフト」としてロシア語に翻訳された重みは、ゼロの値を特徴付ける追加のパラメーターです。
たとえば、よく知られている(あまり正確ではない)数式では、「正しい体重は身長-100に等しくなければなりません」- weight = height - 100 -100-バイアスは-100で、成長の重みは1です。
非線形依存
高次の依存関係を見つける必要があるときに状況が発生することがあります。
調査する良い例の1つは、生存者に関する統計を備えたタイタニックのデータセット(データセット)です。
インタラクティブな視覚化を試してみると、平均してより多くの女性が生き残っていることがわかります。 しかし、詳細を掘り下げると、乗組員と3番目のクラスの間で、生存率がはるかに低かったことに注意してください。 より正確な予測モデルを構築するには、何らかの方法でそれを記述する必要があります-「彼女が女性で、グレード1からの場合、生き残る可能性は+ 10%でした」。
科学者たちは単純なスキームを提案しました-そのようなパラメーターを追加機能と呼び、元の関数で使用します。 つまり、もう1つのxN + 1がx1、x2、x3などに追加されます。これは、最初のクラスの女性の場合は1、そうでない場合は0です。 その後、ますます多くのパラメータが表示され、計算でこれらすべてを考慮し始めます。
数学の言語で「 条件 、次に1、そうでなければ0」という関数をどのように記述できますか?
三項演算子の類似体を作成して問題を真正面から解決すると、関数が得られます。グラフは次のようになります。

しかし、抜け穴をたくさん残しておくことで、より賢くすることができます。 実際、そのようなスケジュールで作業することは困難です。 それとのギャップのために、例えば、デリバティブを取ることや、より多くの興味深いトリックを実行することは不可能です。 したがって、このような「壊れた」関数の代わりに、通常、連続的および連続的に増加する関数、たとえばシグモイド1 / (1 + Math.E ** -x)ます。 次のようになります。
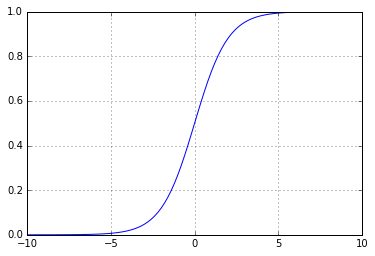
これは非常によく似ています--1では値が0に近く、1では値が1に近くなりますが、より効果的なフィードバックが得られます:受信した値から、元の破線とは異なり、正解がどれだけ近いか遠いかを理解できます正しく答えたのか、間違いをしたのかしかわからない関数:1を取得したが0を期待した場合、同じ0を取得するためにスケジュールに沿ってどれだけ左に移動する必要があるかはわかりません
この機能はアクティベーション機能と呼ばれます。
その結果、次の形式の関数を介して新しいパラメーターを取得します。
const activation_sigmoid = x => 1 / (1 + Math.exp(-x)); function predict(x1, x2, x3..., xN) { return activation_sigmoid( weights.x1 * x1 + weights.x2 * x2 + ... + weights.xN * xN + weights.bias); }
このような関数はパーセプトロンと呼ばれます。
パーセプトロンは、隠れ層のないニューラルネットワークの最も単純な形式です。 視覚的な表現では、次のようになります。

ウィキペディアの記事「ニューラルネットワーク」の写真を見ると、非常に大きな類似性が見られます。

そして、実装の観点からニューラルネットワークの定義に至りました。
古典的なニューラルネットワークは、入力データの線形変換と非線形変換が交互に行われたチェーンです。 例外もありますが、通常は、よりcな(読み取り、非線形)ネットワーク構造を持っています。
画像認識やワードプロセッシングはもちろんのこと、最も単純で最も「標準的な」ケースでは、ニューラルネットワークはレイヤーの集合であり、各レイヤーはニューロンで構成されています。 各ニューロンは、このニューロンの特定の重みを使用して前の層のすべてのパラメーターを要約し、その後、合計を活性化関数に渡します。
これが複雑すぎると思われる場合は、読み進めてください。コードでは、はるかに簡単に見えます。
コード内のニューラルネットワーク
ニューラルネットワークで最も一般的な例はXORの実装です。これは、データサイエンスの学生にとっては一種のHello Worldです。
XORの機能は、それが最も単純な非線形関数であるという事実に正確にあります-線形回帰として実装することは不可能です(読み取り、すべての値に線を引くことはできません)。
彼女のデータセットは次のようになります。
var data = [ {input: [0, 0], output: 0}, {input: [1, 0], output: 1}, {input: [0, 1], output: 1}, {input: [1, 1], output: 0}, ];
そのため、加算と非線形関数を使用して排他的にXORを実装する必要があります。非線形関数は入力で単一の数値を取ります。
この実装は次のようになります(これまでのところ、ニューラルネットワークはありません)。
var activation = x => x >= .5 ? 1 : 0; function xor(x1, x2) { var h1 = activation(-x1 + x2); var h2 = activation(+x1 - x2); return activation(h1 + h2); }
ここで、h1とh2は非表示パラメーターです。
または、重みを追加しようとすると、次のようになります。
var activation = x => x >= .5 ? 1 : 0; var weights = { x1_h1: -1, x1_h2: 1, x2_h1: 1, x2_h2: -1, bias_h1: 0, bias_h2: 0 } function xor(x1, x2) { var h1 = activation( weights.x1_h1 * x1 + weights.x2_h1 * x2 + weights.bias_h1); var h2 = activation( weights.x1_h2 * x1 + weights.x2_h2 * x2 + weights.bias_h2); return activation(h1 + h2); }
ニューラルネットワーク機能はどのように見えますか? さて、重みをランダムな値に置き換えます。
var rand = Math.random; var weights = { i1_h1: rand(), i2_h1: rand(), bias_h1: rand(), i1_h2: rand(), i2_h2: rand(), bias_h2: rand(), h1_o1: rand(), h2_o1: rand(), bias_o1: rand(), };
ネットワークを開始しようとすると、おridgeができます。
今、私たちは「最も正しい重みを見つける」という課題に直面しています。 なぜこれをしたのですか?
XORの場合、この関数が機能する正確なロジックはわかっていますが、実際の条件の場合、記述しようとしているプロセスがどのように機能するかを理解することはほとんどありません。また、データセットである観測セットしかありません。 連絡したこの「ブラックボックス」を再現するようにニューラルネットワークに教えます。通常は、隠れ層に十分な数のノードがある場合はかなりうまく機能します。 さらに、無限数のニューロンを持つ単層ネットワークは、あらゆる関数を無限に高い精度で完全に「エミュレート」できることが数学的に証明されています(普遍近似定理)。
正しい重みを見つけることに戻りましょう。 それを実現するには、まず何を減らしたいかを理解する必要があります。 どれだけ間違えたかを判断できる機能が必要です。 そして、あなたが私たちの重みを変えようとするとき-私たちが正しい方向に動いているかどうかを理解するために。
これらのタスクでは、2つの関数が最も一般的です: 最小二乗法 、二乗誤差の平均をとるとき(たとえば、0から1、または-100から1250までの10の値がある場合、回帰問題に便利です-主なことは彼らはこの範囲にあることができます)と呼ばれる。 LogLossまたはクロスエントロピー 。対数損失推定値。たとえば、ニューラルネットワークで認識される数字または文字を判別しようとする場合の分類問題に有効です。
XORでは、平均二乗誤差を使用します。
const _ = require('lodash'); var calculateError = () => _.mean(data.map(({input: [i1, i2], output: y}) => (nn(i1, i2) - y) ** 2));
学習は軽い
私たちのネットワークを学ぶ時です。
少し後退して、線形回帰がどのように「学習する」かを理解する必要があります。 次のように機能します-同じMSE(平均二乗誤差)があり、それを削減しようとしています。 数学のコースを思い出すと、Xからの正方形のグラフは次のようになります。
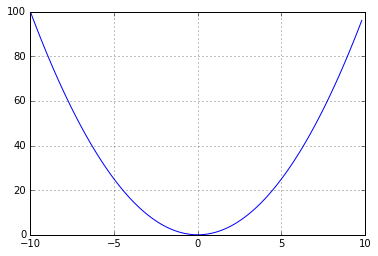
そして、私たちの仕事は、この放物線の最小限にスライドすることです。
この最小値までスライドするには、エラーの多い場所と少ない場所を調べて理解する必要があります。 そして、下に移動します。 これは、数値の方法で行うことができます(+1と-1の値を見て、移動する場所を計算します)、または関数の変化率を特徴付ける微分を数学的に取ることができます。 言い換えれば、パラメータの増加が誤差を増加させる場合、誤差の導関数は正になり(放物線の右側にあります)、逆も同様です。 重みを乗じた微分値を独自の重みに追加し、退屈するまで、またはローカルミニマムに到達するまで、エラーが最小になるように段階的に回答にアプローチします。 簡単に言えば、導関数を取り、それが正の場合、この特定の値については、入力値が増加するとエラーが増加し、減少すると減少します。
視覚的に想像すると、次のようになります。

コメントでは、最初にこの写真はAndrew Ngコースのものであると書いています
エラー関数を(f(x)-y)* 2として表すと、その微分は2 (f(x)-y)f '(x)に等しくなります 。 証明 )
完全に接続された層(つまり、私たちが話しているもの)のニューラルネットワークは、このような線形回帰の連鎖であるため、各層のこの導関数を計算し、重み係数を乗算するだけです。
ライブ
おそらく、何が起こっているのかを説明したコードを表示するだけの時間でしょう。
このような大量のコードをハブに挿入するのはかなり残酷な作業なので、RunKitに多くのコメントを付けてコードを投稿しました。
https://runkit.com/jabher/neural-network-from-scratch-in-js
そしてロシア語:
https://runkit.com/jabher/neural-network-from-scratch-in-js---ru
念のため-gist.github.comのコードの複製
おわりに
もちろん、ニューラルネットワークはもっと複雑です。 たとえば、写真の画像を認識するInception 3スキームを見ることができます。 このようなネットワークには、現在見ているものよりもうまく機能し、学ぶことが難しい多くのトリッキーな層がありますが、本質は同じままです-行列を乗算し、エラーを計算し、反対方向にエラーを緩めます。
また、ニューラルネットワークのフレームワークの開発に参加したい場合は、 Cazalaに参加してください 。