こんにちはHabr! a
5 + b
5 + c
5 + d
5 = e
5の形のディオファントス方程式を解くためのプログラムのいくつかの改良版を書くことにより、オイラー仮説
に関する 一連の 記事を続けることにしました。
ご存知のように、複雑な計算上の問題を解決するには、少なくとも次の点に注意する必要があります。
- 効率的なアルゴリズム
- 迅速な実装
- 強力な鉄
- 並列化
最初の点に最も注意を払いました。 その結果を見てみましょう。
すぐに、コードがC ++で記述され、32ビットMS Visual C ++ 2008コンパイラがコンパイルされ、i5-2410M 2.3Ghzマシンのシングルスレッドで起動されたことに注目します。 それほど強力ではないラップトップに横たわっている間にコードを書く方が便利で、64ビットコンパイラが面倒だというだけです。 ブラウザーなどの他のプロセスが動作時間にわずかに影響を与える可能性がある一方で、コードが測定のために1回以上実行されることはめったにないため、時間測定は正確に輝きません。 ただし、私たちの目的では、精度は許容範囲です。
それでも、
Dimchanskyの提出により、a、b、c、d、e> 0の上記の方程式の整数解を探すことを明確にします。 3番目の解決策がありますが、変数は負の値を取ることができます。 それらはすべて
ここにあります 。
Oの物語#1(n 5 )
可能な限り愚かな解決策から始めましょう。 コード:
コードlong long gcd( long long x, long long y ) { while (x&&y) x>y ? x%=y : y%=x; return x+y; } void tale1( int n ) { for (int a=1; a<=n; a++) for (int b=a+1; b<=n; b++) for (int c=b+1; c<=n; c++) for (int d=c+1; d<=n; d++) for (int e=d+1; e<=n; e++) { long long a5 = (long long)a*a*a*a*a; long long b5 = (long long)b*b*b*b*b; long long c5 = (long long)c*c*c*c*c; long long d5 = (long long)d*d*d*d*d; long long e5 = (long long)e*e*e*e*e; if (a5 + b5 + c5 + d5 == e5) if (gcd( a, gcd( gcd( b, c ), gcd( d, e ) ) ) == 1) printf( "%d^5 + %d^5 + %d^5 + %d^5 = %d^5\n", a, b, c, d, e ); } }
実際、これは最も愚かなものではありません。1からnまでのすべての変数を操作し、最後にa <b <c <d <eであることを確認できるためです。 しかし、それから私はあまりにも長く待たなければなりません。 作業時間:
長所:フェルトブーツのようにシンプルで、すぐに記述でき、O(1)メモリが必要であり、古典的な解27
5 + 84
5 + 110
5 + 133
5 = 144
5を見つけます。
短所: 禁止されています。
Oの物語#2(n 4 log n)
ソリューションを少しスピードアップしましょう。 実際、このオプションは同志
drBasicによって提案されたものと同等
です 。
コード void tale2( int n ) { vector< pair< long long, int > > vec; for (int a=1; a<=n; a++) vec.push_back( make_pair( (long long)a*a*a*a*a, a ) ); for (int a=1; a<=n; a++) for (int b=a+1; b<=n; b++) for (int c=b+1; c<=n; c++) for (int d=c+1; d<=n; d++) { long long a5 = (long long)a*a*a*a*a; long long b5 = (long long)b*b*b*b*b; long long c5 = (long long)c*c*c*c*c; long long d5 = (long long)d*d*d*d*d; long long sum = a5+b5+c5+d5; vector< pair< long long, int > >::iterator it = lower_bound( vec.begin(), vec.end(), make_pair( sum, 0 ) ); if (it != vec.end() && it->first==sum) if (gcd( a, gcd( gcd( b, c ), gcd( d, it->second ) ) ) == 1) printf( "%d^5 + %d^5 + %d^5 + %d^5 = %d^5\n", a, b, c, d, it->second ); } }
ここで配列を作成し、1からnまでのすべての数値の5乗を格納します。次に、バイナリ検索で4つのネストされたループ内で、数値a
5 + b
5 + c
5 + d
5が配列にあるかどうかを確認します。
| n | 時間#1 | 時間#2 |
|---|
| 100 | 1563ms | 318ms |
| 200 | 40代 | 4140ms |
| 500 | 74m | 189 |
| 1000 | | 55m |
このオプションはすでに高速で実行されており、プログラムがn = 1000で動作し終わるのを待つ忍耐さえありました。
長所:まだ非常にシンプルで、愚かなソリューションよりも速く、書くのが簡単で、古典的なソリューションを見つけます。
短所: O(n)メモリが必要
ですが、まだ
抑制されています。
O(n 4 log n)の物語#3、ただしO(1)メモリ
実際、すべての学位を配列に保存し、そこでビンポ検索で何かを探すのは意味がありません。 この配列の位置iの番号はすでにわかっています。 「仮想」アレイで単純にビン検索を実行できます。 すぐに言ってやった:
コード void tale3( int n ) { for (int a=1; a<=n; a++) for (int b=a+1; b<=n; b++) for (int c=b+1; c<=n; c++) for (int d=c+1; d<=n; d++) { long long a5 = (long long)a*a*a*a*a; long long b5 = (long long)b*b*b*b*b; long long c5 = (long long)c*c*c*c*c; long long d5 = (long long)d*d*d*d*d; long long sum = a5+b5+c5+d5; if (sum <= (long long)n*n*n*n*n) { int mi = d, ma = n;
これで配列は不要になり、純粋なバイナリ検索ができました。
| n | 時間#1 | 時間#2 | 時間#3 |
|---|
| 100 | 1563ms | 318ms | 490ms |
| 200 | 40代 | 4140ms | 6728ms |
| 500 | 74m | 189 | 352秒 |
| 1000 | | 55m | |
残念ながら、おそらくビン検索内で毎回5乗を再計算するため、ランタイムは低下しました。 いいでしょう
長所: O(1)メモリが必要で、古典的なソリューションを見つけます。
短所:以前のソリューションよりも遅い。
Oの物語#4(n 4 )
方程式をもう一度見てみましょう。
a
5 + b
5 + c
5 + d
5 = e
5または、簡単にするために、A =B。
アルゴリズムに4つのネストされたループを実行させます。 値a、b、およびcを修正し、dおよびeの値の動作を確認します。 いくつかのd = xについて、A <= Bがyと等しいeの最小値とします。 d = xの場合、値e> yを考慮することは意味がありません。 また、d = x + 1の場合、A <= Bであるeの最小値はy以上です。 つまり、dに沿ってeの値をいつでも穏やかに増やすことができ、これにより何も見逃すことがなくなります。 dとeの値は増加するだけなので、それらに沿った一般的な経過にはO(n)時間かかります。 この考え方は、2ポインターメソッドと呼ばれます。
コード void tale4( int n ) { for (int a=1; a<=n; a++) for (int b=a+1; b<=n; b++) for (int c=b+1; c<=n; c++) { int e = c+1; for (int d=c+1; d<=n; d++) { long long a5 = (long long)a*a*a*a*a; long long b5 = (long long)b*b*b*b*b; long long c5 = (long long)c*c*c*c*c; long long d5 = (long long)d*d*d*d*d; long long sum = a5+b5+c5+d5; while (e<n && (long long)e*e*e*e*e < sum) e++; if (sum == (long long)e*e*e*e*e) if (gcd( a, gcd( gcd( b, c ), gcd( d, e ) ) ) == 1) printf( "%d^5 + %d^5 + %d^5 + %d^5 = %d^5\n", a, b, c, d, e ); } } }
コードはビン検索の場合よりも少なく、より多くの利点があります。
| n | 時間#1 | 時間#2 | 時間#3 | 時間#4 |
|---|
| 100 | 1563ms | 318ms | 490ms | 360ms |
| 200 | 40代 | 4140ms | 6728ms | 4339ms |
| 500 | 74m | 189 | 352秒 | 177 |
| 1000 | | 55m | | 46m |
隠された定数が大きいため、このソリューションは、ソリューション番号2をO(n
4 log n)で500のオーダーでのみ追い越し始めます。もちろん、5番目の累乗をより慎重に計算することで加速できますが、それを行いません。
長所:ソリューション#2よりも漸近的に高速であるため、O(1)メモリが必要です。 はい、そうです。
短所:最適とはほど遠い、大きな隠れた定数。
Oの物語#5(n 3 )
2つのポインターを使用してアイデアを開発し、ソリューションの残りの部分を逆さまにしましょう。 方程式A + B = Cがあり、A、B、Cのそれぞれについて、それらを選択するn(A)、n(B)、n(C)の方法があるとします。 Cの値を修正し、AとBのすべての有効な値を昇順でソートしましょう。 次に、2つのポインターを使用してAとBの値に沿って実行し、O(n(A)+ n(B))について、Cの現在の値に必要なすべてをチェックします! つまり、いくつかの固定Aについては、Bの値を減らしますが、A + B> Cです。 A + B <= Cになるとすぐに、Bをさらに減らす意味はありません。 次に、Aを増やし、Bを減らすプロセスを続けます。アルゴリズム全体はO(n(A)log n(A)+ n(B)log n(B)+(n(A)+ n(B))n( C))。
AとBが同じセットの要素である場合、現在のAとBが一致するとすぐに、固定Cをチェックするアルゴリズムを停止できます(一般性を失うことなく、A <Bと仮定できるため)。
ここで、方程式では、Aに対して(a
5 + b
5 )、Bに対して(c
5 + d
5 )、Cに対してe
5を示します。そして、次のコードを記述します。
コード void tale5( int n ) { vector< pair< long long, int > > vec; for (int a=1; a<=n; a++) for (int b=a+1; b<=n; b++) { long long a5 = (long long)a*a*a*a*a; long long b5 = (long long)b*b*b*b*b; if (a5 + b5 < (long long)n*n*n*n*n)
ペア(a、b)(および(c、d))の順序はn
2であるため、ソートにはO(n
2 log n)が必要になり、ポインターを使用した以降のチェックはO(n
3 )になります。 総ネットキューブ。
エクササイズ 。 上記のコードで論理エラーを見つけます。
答えを見る前に数分考えてください。私たちの場合、ソートされた配列では、理論的には同じ合計が落ち、2つのポインターがいくつかの等式をスキップする可能性があります。 しかし、実際には、それらはすべて次の推論とは異なります:偶然の一致がある場合、x、y、z、tについてx ^ 5 + y ^ 5 = z ^ 5 + t ^ 5であり、
この仮説に対する反例を見つけました。 修正として、あなたができる最も簡単なことは、すべての数値が本当に異なることを確認することです。
| n | #1 | #2 | #3 | #4 | #5 |
|---|
| 100 | 1563ms | 318ms | 490ms | 360ms | 82ms |
| 200 | 40代 | 4140ms | 6728ms | 4339ms | 121ms |
| 500 | 74m | 189 | 352秒 | 177 | 516ms |
| 1000 | | 55m | | 46m | 3119ms |
| 2000年 | | | | | 22秒 |
| 5000 | | | | | 328 |
大幅な加速により、許容可能な時間内でn = 5000をドラッグできます。 オーバーフローを回避するために、配列にペアを追加するときに必要なチェック。
長所:おそらく最速の漸近アルゴリズム。
短所:隠され
た大きな定数で、最大5000のオーダーのnまでしか機能せず、O(n
2 )のメモリを消費します。
信じられないほど小さな隠れた定数を持つO(n 4 log n)の物語#6
突然。
このコメントからのユーザーの提出
erwins22から、5乗を11で除算することによって得られる残差を考慮します。つまり、aをx
5 = a mod 11と比較できるものです
。aの可能な値は0、1および-1(mod 11)(ご自身で確認してください)。
次に、等式a
5 + b
5 + c
5 + d
5 = e
5ユニットとマイナスユニットでは、合計数は偶数であり(パリティが収束するように互いにバランスをとる必要があります)、数a、b、c、 d、eは0からモジュール11まで、つまり11で割った値に相当します。1方向に分けて、2つのオプションのいずれかを取得します。
(a
5 + b
5 )+(c
5 + d
5 )= e
5 ; e = 0 mod 11
(e
5 -a
5 )-(b
5 + c
5 )= d
5 ; d = 0 mod 11
信じられませんが、数値xが11で割り切れる場合、数値x
5は161051で割り切れます。したがって、上記の等式の左側は161051で割り切れるはずです。 ご覧のとおり、上記の式では、括弧を使用して既にいくつかの数値が慎重にペアリングされています。 ここで、最初のブラケットを修正すると、2番目のブラケットは161051で割ったときにすべての可能な161051残基のうちの1つだけを持つことができます。したがって、O すべてを調べて、結果が正確な5度(たとえば、5度の配列の双眼鏡)であるかどうかを確認すると、O(n
4 log n / 161051)ですべての解が見つかります。 コード:
コード void tale5( int n ) { vector< pair< long long, int > > vec; for (int a=1; a<=n; a++) for (int b=a+1; b<=n; b++) { long long a5 = (long long)a*a*a*a*a; long long b5 = (long long)b*b*b*b*b; if (a5 + b5 < (long long)n*n*n*n*n)
このソリューションの作業時間:
| n | #1 | #2 | #3 | #4 | #5 | #6 |
|---|
| 100 | 1563ms | 318ms | 490ms | 360ms | 82ms | 129ms |
| 200 | 40代 | 4140ms | 6728ms | 4339ms | 121ms | 140ms |
| 500 | 74m | 189 | 352秒 | 177 | 516ms | 375ms |
| 1000 | | 55m | | 46m | 3119ms | 2559ms |
| 2000年 | | | | | 22秒 | 38代 |
| 5000 | | | | | 328 | 28m |
この表は、n = 500およびn = 1000の場合、このソリューションが立方体のソリューションを追い抜くことさえ示しています。 しかし、それでもキュービックソリューションは強く追い越し始めます。 漸近的、彼女は-あなたは彼女を欺くことはできません。
長所:非常に強力なクリッピング。
短所:漸近的な動作が大きいため、このアイデアを3次解に結び付ける方法は明確ではありません。
物語#7 O(n 3 )の128ビット数
モジュールのトリックを一時的に忘れましょう(少し後で覚えます!)そして、キュービックソリューションをやり直して、n> 5000で正しく動作するようにします。 これを行うために、128ビット整数を実装します。
コード typedef unsigned long long uint64; typedef pair< uint64, uint64 > uint128; uint128 operator+ (const uint128 & a, const uint128 & b) { uint128 re = make_pair( a.first + b.first, a.second + b.second ); if ( re.second < a.second ) re.first++; return re; } uint128 operator- (const uint128 & a, const uint128 & b) { uint128 re = make_pair( a.first - b.first, a.second - b.second ); if ( re.second > a.second ) re.first--; return re; } uint128 power5( int x ) { uint64 x2 = (uint64)x*x; uint64 x3 = (uint64)x2*x; uint128 re = make_pair( (uint64)0, (uint64)0 ); uint128 cur = make_pair( (uint64)0, x3 ); for (int i=0; i<63; i++) { if ((x2>>i)&1) re = re + cur; cur = cur + cur; } return re; } void tale7( int n ) { vector< pair< uint128, int > > vec = vector< pair< uint128, int > >( n*n/2 ); uint128 n5 = power5( n ); int ind = 0; for (int a=1; a<=n; a++) for (int b=a+1; b<=n; b++) { uint128 a5 = power5( a ); uint128 b5 = power5( b ); if (a5 + b5 < n5) vec[ind++] = make_pair( a5+b5, (a<<16)+b ); } sort( vec.begin(), vec.begin()+ind ); for (int e=1; e<=n; e++) { uint128 e5 = power5( e ); int i = 0, j = ind-1; while( i < j ) { while ( i < j && vec[i].first + vec[j].first > e5 ) j--; if ( vec[i].first + vec[j].first == e5 ) { int a = (vec[i].second >> 16); int b = (vec[i].second & ((1<<16)-1)); int c = (vec[j].second >> 16); int d = (vec[j].second & ((1<<16)-1)); if (b < c && gcd( a, gcd( gcd( b, c ), gcd( d, e ) ) ) == 1) printf( "%d^5 + %d^5 + %d^5 + %d^5 = %d^5\n", a, b, c, d, e ); } i++; } } }
完了する必要のあった操作は、加算と5乗です。 まだ減算があり、このソリューションでは必要ありませんが、後で必要になります。 したがって、それをさせてください。 128ビットの数値はペアとして実装されているため、既に<、>、=操作があり、必要に応じて正確に機能します。
最初に、ベクトルのサイズをすぐに設定します。 最適化のためにこれが行われているわけではありません。64ビットコンパイラを発見するには遅すぎます。32ビットで使用できるメモリは2 GBのみです。 n = 10000の場合、ベクターごとに約1.2 GBが必要です。 push_backを使用してベクトルを展開すると、展開中に最後に2 GB以上をキャプチャします(長さNから2 * Nに増やすには、3 * Nの中間メモリが必要です)。
| n | #1 | #2 | #3 | #4 | #5 | #6 | #7 |
|---|
| 100 | 1563ms | 318ms | 490ms | 360ms | 82ms | 129ms | 20ms |
| 200 | 40代 | 4140ms | 6728ms | 4339ms | 121ms | 140ms | 105ms |
| 500 | 74m | 189 | 352秒 | 177 | 516ms | 375ms | 1014ms |
| 1000 | | 55m | | 46m | 3119ms | 2559ms | 7096ms |
| 2000年 | | | | | 22秒 | 38代 | 52代 |
| 5000 | | | | | 328 | 28m | 13m |
| 10,000 | | | | | | | 89m |
プログラムがソリューション#5に比べてほぼ2倍遅くなったことがわかりますが、新しい難攻不落のピークn = 10000を征服しました!
長所: n> 5000でオーバーフローしないようになりました。
短所:解決策5の2倍遅く動作し、大量のメモリを消費します。
隠された定数が小さいO(n 3 )の物語#8
11で割ったときの剰余についてもう一度思い出してください。2つの等式があります。
(a
5 + b
5 )+(c
5 + d
5 )= e
5 ; e = 0 mod 11
(e
5 -a
5 )-(b
5 + c
5 )= d
5 ; d = 0 mod 11
11を法とする5度の剰余には常に0、1、または-1の剰余があります。 a <b <c <dという形式の制約を削除し、数値をあるブラケットから別のブラケットに任意に移動させます。 その後、(すべてのケースを考慮することにより)各ブラケットが11を法として0に等しくなるようにいつでも移動できることを示すのは簡単です。それでは、1からnまでの数字のすべてのペアをソートし、5度の合計と差を見つけ、 11で割り切れるものだけを覚えておいてください。そして、残りのペアは単純に捨てることができます。
この事実を定式化できます。そのようなペアの数は、ペアの総数の約51/121になります(これがなぜそうなのかを考えてください)。 残念ながら、このようなペアの2つの配列を保存する必要があります(合計と差分)。これにより、メモリゲインは102/121になります。 まあ、15%も削減です。 しかし、その後、これらの配列で少し実行する必要があります。
最後に、最良のニュース:変数の1つ(キュービックソリューションで最も外部的)を11のステップで整理するのが理にかなっています。悪いニュースは、両方のタイプの等式を別々に解決する必要があるということです。 悲しいことに、悲しいことに、これは、ソリューション#6のように11
5倍ではなく、プログラムを11倍だけ高速化します(実際、まだ事実ではありません)。
コード void tale8( int n ) { vector< pair< uint128, pair< int, int > > > vec_p, vec_m; uint128 n5 = power5( n ); for (int a=1; a<=n; a++) for (int b=1; b<a; b++) { uint128 a5 = power5( a ); uint128 b5 = power5( b ); int A = a%11; int B = b%11; int A5 = (A*A*A*A*A)%11; int B5 = (B*B*B*B*B)%11; if ( (A5+B5)%11 == 0 ) vec_p.push_back( make_pair( a5+b5, make_pair( a, b ) ) ); if ( (A5-B5+11)%11 == 0) vec_m.push_back( make_pair( a5-b5, make_pair( a, b ) ) ); } sort( vec_p.begin(), vec_p.end() ); sort( vec_m.begin(), vec_m.end() );
ここでは、ベクターの展開により、幸運であり、n = 10000のプログラムは2GBに収まります。
| n | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 |
|---|
| 100 | 1563ms | 318ms | 490ms | 360ms | 82ms | 129ms | 20ms | 16ms |
| 200 | 40代 | 4140ms | 6728ms | 4339ms | 121ms | 140ms | 105ms | 49ms |
| 500 | 74m | 189 | 352秒 | 177 | 516ms | 375ms | 1014ms | 472ms |
| 1000 | | 55m | | 46m | 3119ms | 2559ms | 7096ms | 2110ms |
| 2000年 | | | | | 22秒 | 38代 | 52代 | 13秒 |
| 5000 | | | | | 328 | 28m | 13m | 161s |
| 10,000 | | | | | | | 89m | 20m |
悲しいかな、プログラムは4.5倍だけ加速しました。 ご覧のとおり、2番目の式の多数のチェックにより、隠れた定数が大きく損なわれています。 まあ、何も、最適化の余地はまだありません。 今最大の問題:野生のメモリ消費。 現在のレコードに間に合うようにnがすでに許容できる場合、メモリからは適合しなくなります。
長所:おそらく最速のソリューションが提案されました。
短所:依然としてメモリ消費量が多いという問題。
O(n 3 log n)のメモリ消費量がO(n)の場合の物語#9
メモリ消費をどのように削減しますか?
ここで説明したトリックを活用しましょう。 すなわち、nよりも大きい素数pを取りますが、あまり多くは取りません。 私たちが持っている最初の方程式を考えます(2番目の方程式も同様に考えられます):
(a
5 + b
5 )+(c
5 + d
5 )= e
5 ; e = 0 mod 11
次に、(a
5 + b
5 )= w mod pを0からp-1までの一部のwとします。 この比較を満たすペア(a、b)の数は線形数です。 これを示すために、パラメーターaを1からnまで繰り返します。 次に、bを見つけるには、b
5 =(w-a
5 )= u mod pという比較を解く必要があります。 そして、この比較には常に1つ以上の解決策はないと主張されています。 これは、
e-maxxのこのページから続きます。 そこで、1つからすべての解を得るための公式に注意を払う必要があります。
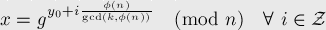
つまり、すべての解の中で、gcd(5、phi(p))= gcd(5、p-1)です。 つまり、p = 5q + 1の場合、5つのソリューション(またはなし)があり、残りのケースでは1つしかソリューションがありません。
(ちなみに、この式の由来と動作はわかりません。ソースを知っている人がいる場合は、どこで明確に記述されているか、リンクを共有してください。)
ここで問題は、固定uのbを見つける方法ですか? これを一度だけ、しかし迅速に行うには、数字の理論をかなり理解する必要があります。 しかし、uのすべての可能な値に対してbが必要なので、各bに対してuを見つけてプレートに書き込むことができます。そのようなuの場合、そのような解はbです。
さらに、固定wおよび固定e
5の場合、(c
5 + d
5 )=(e
5 -w)mod pが得られます。 比較を満たす線形の数のペアもあります。
つまり、固定のwと固定のeに対して、ソートする必要がある線形の数のペアを取得し(残念なことに、漸近線の余分な対数がここに表示されます)、2つのポインターを使用します。 wとeの異なる値は次数O(n)であるため、一般的な漸近挙動はO(n
3 log n)です。
怖いテストコードを書きましょう:
コード bool is_prime( int x ) { if (x<2) return false; for (int a=2; a*a<=x; a++) if (x%a==0) return false; return true; } void tale9( int n ) { int p = n+1; while ( p%5==1 || !is_prime( p ) ) p++; vector< int > sols = vector< int >( p, -1 ); for (int i=1; i<=n; i++) { uint64 tmp = ((uint64)i*i)%p; tmp = (((tmp*tmp)%p)*i)%p; sols[(unsigned int)tmp] = i; } for (int w=0; w<p; w++) {
この残酷なブリキを実行します:| n | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 |
|---|
| 100 | 1563ms | 318ms | 490ms | 360ms | 82ms | 129ms | 20ms | 16ms | 219ms |
| 200 | 40代 | 4140ms | 6728ms | 4339ms | 121ms | 140ms | 105ms | 49ms | 1741ms |
| 500 | 74m | 189 | 352秒 | 177 | 516ms | 375ms | 1014ms | 472ms | 25秒 |
| 1000 | | 55m | | 46m | 3119ms | 2559ms | 7096ms | 2110ms | 200代 |
| 2000年 | | | | | 22秒 | 38代 | 52代 | 13秒 | 28m |
| 5000 | | | | | 328 | 28m | 13m | 161s | |
| 10,000 | | | | | | | 89m | 20m | |
紳士、石器時代へようこそ!なぜそれは不敬lyに遅くなるのですか?そうそう、3つの入れ子になったループの一番下にpower5()関数があり、ループ内で既に63回の反復が行われています。組み込み関数を書き換えますか?静かに、次のソリューションでは、事前に計算されたプレートから答えをドラッグするだけです。しかし、今ではメモリをほとんど消費せず、1つの非常に便利なプロパティが登場しました。タスクを独立したサブタスクに分割できるようになりました。つまり、「並列化」、つまり計算を複数のコアに分散できますつまり、各コアに対して、パラメーターwの独自の値を指定します。これらのwを0からp-1までのすべての数値でカバーする場合、問題のすべてのケースをカバーしますが、すべてのカーネルの負荷はほぼ均等に分散されます。長所:わずかなメモリしか消費せず、分散コンピューティングをサポートします。短所:二日酔いの靴屋のように遅くなります。筋金入りの最適化によるO(n 3 log n)の物語#10
ソリューション#9を採用し、ハードコアな最適化を追加します。まあ、実際、彼らはそれほどハードコアではありません。しかし、それらの多くがあります。- 計算のみ可能なすべてを計算し、タブレットに配置します。
- push_backsでベクターを拒否し、静的配列ですべてをやり直します。
- 可能な限り、除算の残りを実行する操作を削除します。
- ペアの配列では、5度の合計(または差)のみを保存し、解が見つかった場合にのみペア自体が回復を試みます(解は非常にまれであるため、ペアは正方形について愚かに検索されます)。
- eとdによってループ内で生成される配列は、平均で2倍短くなりました。実際、(a 5 + b 5)+(c 5 + d 5)= e 5の場合、(c 5 + d 5)<e 5(小さなeに適しています)、および(e 5 -a 5)-(b 5 + c 5)= d 5(e 5 -a 5)> d 5(大きなdに適しています)のみに関心があります。
そして、コードを取得します。コード #define MAXN 100500 int pow5modp[MAXN]; int sols[MAXN]; uint128 vec1[MAXN], vec2[MAXN]; int vec1_sz, vec2_sz; uint128 pow5[MAXN]; int pow5mod11[MAXN]; void init_arrays( int n, int p ) { for (int i=1; i<=n; i++) { uint64 i5p = ((uint64)i*i)%p; i5p = (((i5p*i5p)%p)*i)%p; pow5modp[i] = (int)i5p; } for (int i=0; i<p; i++) sols[i] = -1; for (int i=1; i<=n; i++) sols[pow5modp[i]] = i; for (int i=1; i<=n; i++) pow5[i] = power5(i); for (int i=1; i<=n; i++) { int ii = i%11; pow5mod11[i] = (ii*ii*ii*ii*ii)%11; } } void tale10( int n, int start=0, int step=1 ) { int p = n+1; while ( p%5==1 || !is_prime( p ) ) p++; init_arrays( n, p ); for (int w=start; w<p; w+=step) { cerr << "n=" << n << " p=" << p << " w=" << w << "\n"; // (a^5 + b^5) + (c^5 + d^5) = e^5 // (a^5 + b^5) = w (mod p) vec1_sz = 0; for (int a=1; a<=n; a++) { int tmp = w - pow5modp[a]; int b = sols[ tmp<0 ? tmp+p : tmp ]; if (b!=-1 && b<a) if ( (pow5mod11[a]+pow5mod11[b])%11 == 0 ) vec1[vec1_sz++] = pow5[a]+pow5[b]; } sort( vec1, vec1 + vec1_sz ); for (int e=11; e<=n; e+=11) { // (a^5 + b^5) + (c^5 + d^5) = e^5 // (a^5 + b^5) = w (mod p) // (c^5 + d^5) = (e^5 - w) = q (mod p) int q = (int)((pow5modp[e] - w + p)%p); uint128 e5 = pow5[e]; vec2_sz = 0; for (int c=1; c<e; c++) { int tmp = q - pow5modp[c]; int d = sols[ tmp<0 ? tmp+p : tmp ]; if (d!=-1 && d<c) if ( pow5mod11[c]+pow5mod11[d]==0 || pow5mod11[c]+pow5mod11[d]==11 ) { uint128 s = pow5[c]+pow5[d]; if (s < e5) vec2[vec2_sz++] = s; } } sort( vec2, vec2 + vec2_sz ); int i = 0, j = vec2_sz-1, mx_i = vec1_sz-1; while( i < mx_i && j >= 0 ) { while ( j >= 0 && vec1[i] + vec2[j] > e5 ) j--; if ( j >= 0 && vec1[i] + vec2[j] == e5 ) { int a=-1, b=-1, c=-1, d=-1; for (int A=1; A<=n; A++) for (int B=1; B<A; B++) if (pow5[A]+pow5[B]==vec1[i]) { a=A; b=B; } for (int C=1; C<=n; C++) for (int D=1; D<C; D++) if (pow5[C]+pow5[D]==vec2[j]) { c=C; d=D; } if (gcd( a, gcd( gcd( b, c ), gcd( d, e ) ) ) == 1) printf( "%d^5 + %d^5 + %d^5 + %d^5 = %d^5\n", a, b, c, d, e ); } i++; } } // (e^5 - a^5) - (b^5 + c^5) = d^5 // (b^5 + c^5) = w (mod p) // already computed as vec1 for (int d=11; d<=n; d+=11) { // (e^5 - a^5) = (d^5 + w) = q (mod p) int q = (int)((pow5modp[d] + w)%p); uint128 d5 = pow5[d]; vec2_sz = 0; for (int e=d+1; e<=n; e++) { int tmp = pow5modp[e]-q; int a = sols[ tmp<0 ? tmp+p : tmp ]; if (a!=-1 && a<e) if ( pow5mod11[e]==pow5mod11[a] ) { uint128 s = pow5[e]-pow5[a]; if (s > d5) vec2[vec2_sz++] = s; } } sort( vec2, vec2 + vec2_sz ); int i = 0, j = 0, mx_i = vec2_sz, mx_j = vec1_sz; while (i < mx_i && j < mx_j) { while (j < mx_j && vec2[i] > vec1[j] && vec2[i] - vec1[j] > d5) j++; if ( j < mx_j && vec2[i] > vec1[j] && vec2[i] - vec1[j] == d5 ) { int e=-1, a=-1, b=-1, c=-1; for (int E=1; E<=n; E++) for (int A=1; A<E; A++) if (pow5[E]-pow5[A]==vec2[i]) { e = E; a = A; } for (int B=1; B<=n; B++) for (int C=1; C<B; C++) if (pow5[B]+pow5[C]==vec1[j]) { b = B; c = B; } if (gcd( a, gcd( gcd( b, c ), gcd( d, e ) ) ) == 1) printf( "%d^5 + %d^5 + %d^5 + %d^5 = %d^5\n", a, b, c, d, e ); } i++; } } } }
コードは、よりコンパクトでシンプルで親切になりました。そして彼はより速くなりました:| n | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 |
|---|
| 100 | 1563ms | 318ms | 490ms | 360ms | 82ms | 129ms | 20ms | 16ms | 219ms | 8ms |
| 200 | 40代 | 4140ms | 6728ms | 4339ms | 121ms | 140ms | 105ms | 49ms | 1741ms | 30ms |
| 500 | 74m | 189 | 352秒 | 177 | 516ms | 375ms | 1014ms | 472ms | 25秒 | 379ms |
| 1000 | | 55m | | 46m | 3119ms | 2559ms | 7096ms | 2110ms | 200代 | 2993ms |
| 2000年 | | | | | 22秒 | 38代 | 52代 | 13秒 | 28m | 24秒 |
| 5000 | | | | | 328 | 28m | 13m | 161s | | 405s |
| 10,000 | | | | | | | 89m | 20m | | 59m |
多少の惨めな10 MBのメモリを使用して、n = 10000のすべてのオプションを多少許容できる時間でチェックしました。長所:十分に速く、ほとんどメモリを消費しません。短所:そうではありません。おとぎ話にも、説明するペンにもありません
そして今、私は64ビットのコンパイラー、6コアのi7-5820K 3.3GHzと4コアのi7-3770 3.4GHzをワイドレッグから取り出し、16の独立したストリームで数日間ソリューション#10を実行します。| n | 総コア | リアルタイム | ストリーム |
|---|
| 10,000 | 29m | 29m | 1 |
| 20000 | 318m | 58m | 6 |
| 50,000 | 105時間 | 7時間 | 16 |
| 100,000 | 970h | 62時間 | 16 |
n = 100000の正確な時間00 221897112ms
01 221697012ms
02 221413313ms
03 219200228ms
04 222362721ms
05 221386814ms
06 221880726ms
07 219676217ms **
08 222212701ms
09 221865811ms
10 213299815ms *
11 211880251ms
12 211634584ms **
13 210114095ms
14 211691320ms *
15 212125515ms
* found 27^5 + 133^5 + 133^5 + 110^5 = 144^5
** found 85282^5 + 28969^5 + 28969^5 + 55^5 = 85359^5
00-09 : i7-5820K 3.3GHz
10-15 : i7-3770 3.4GHz
sum ~ 970h
max ~ 62h
より高速なマシンでの64ビットプログラム(以前にi5-2410M 2.3Ghzでコードをテストしたことを思い出してください)は、約2倍速く動作します。その結果、ドラッグN = 100000に管理され、所望のディオファントス方程式の第二の解決策を見つけること:55 5 + 3183 5 + 28969 5 + 85282 5 = 85359 5おとぎ話はうそですが、その中のヒント
そのため、ここでは最速の漸近的振る舞いが実際には最良ではない最速のソリューションではありません。理論的には、コードを高速化するか、対数を漸近線から切り捨てることができますが、現時点では最適化にうんざりしています-すでに十分な時間を失っています。解決策の対数に関しては、クイックソートを基数ソートに置き換えます(ただし、定数は宇宙次元に増加します)、または2つのポインターのアイデアの代わりにハッシュテーブルを使用します(ここでは、どちらが実際に速いかを既に確認して確認する必要があります)。プロファイリングにより、n = 10000の場合、ソートは全体の約半分になります。つまり、nの値が小さい場合、対数は非常に許容範囲です。加速に関しては、確かに、プログラムを5〜10倍高速化できるモジュールにはまだいくつかのトリックがあります。ドラッグ?
また、nを100万個まですべてチェックするというワイルドなアイデアもあります。予想される検証時間は、原則として現実的であり、約100万コア時間です。しかし、これに対する私の能力は明らかに十分ではありません。一緒に引っ張る?しかし、誰が既に整理したかについての情報は見つかりませんでした。すべてが長い間数えられてきたので、百万まで調べても意味がないかもしれません。誰かがこれに関する情報を持っているなら、退会してください。これで物語は終わり、誰がマスターしたか-よくやった!