はじめに
この記事では、暗号、情報およびコーディング理論、その他の科学で使用される有限体（またはガロア体）の構築と操作のトピックについて説明します。 幅広い実用化があります。 グループ/リング/フィールドのドライ理論は、
Paul Galoisのリンクで読むことができます。ここでは、Scala言語のより多くの実践と実装があります。
種類と制限
まず、Scala言語の
Int型のサイズを考慮して、メモリ内の多項式の表現に関連する技術的な問題について説明する必要があります。 要件は以下のリストに記載されています。
- Scala / JavaのInt型のサイズは32ビットです
- ビットを使用できます：0..30-31、32番目のビットが署名されているため
- 多項式は、0..29の範囲の数値で表す必要があります
- 既約多項式（またはモジュール）の範囲は1..30です
- 最終フィールドには
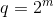要素
実装
最初に、多項式と4つの演算を実装する
Polynomialクラスについて説明します。 このタイプの多項式は「半完成品」であり、有限体に結び付けられていません。
class Polynomial(_p: Int) { val polynomial: Int = _p def order: Int = = { ... } def mul(p: Polynomial): Polynomial = { ... } def div(p: Polynomial): (Int, Int) = { ... } def add(p: Polynomial): Polynomial = { ... } def sub(p: Polynomial): Polynomial = { ... } override def toString: String = Integer.toBinaryString(this.polynomial) }
次は抽象クラス
FiniteFieldです 。これはガロア体の親になります。
FiniteFieldの内部には、内部クラス
FiniteFieldPolynomialが含まれています。この構造により、操作中のセキュリティを確保できます。
安全性は、演算が1つのフィールドからの多項式でのみ実行できるという事実にあります。
モジュロメンバに注意してください。これは体次数のモジュール（または既約多項式）です。
abstract class FiniteField(_initBitNumber: Int) { type T = Polynomial type GFPolynomial <: FiniteFieldPolynomial protected val checkBitNumber: Int => Int = ??? val modulo: T val bits: Int = checkBitNumber(_initBitNumber) protected def createModulo(): Option[Int] def createPolynomial(_initPolynomial: Int): FiniteFieldPolynomial abstract class FiniteFieldPolynomial { protected val p: T def +(other: GFPolynomial): GFPolynomial def -(other: GFPolynomial): GFPolynomial = { this + other } def *(other: GFPolynomial): GFPolynomial def /(other: GFPolynomial): GFPolynomial = this * other.mulInverse def addInverse: GFPolynomial = self def mulInverse: GFPolynomial def self: GFPolynomial } }
ガロア体を作成する際の重要なステップは、体の次数の既約多項式の計算と、それらの1つの選択です。 このプロセスの数学は、リンク
既約多項式で見つけることができます。
既約多項式は、数体の素数のように、乗算および除算に使用されます
。
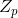
言い換えると、既約多項式は、多項式セットで整数セットの素数と同じ役割を果たします。
多くの既約多項式を見つけるための簡略化されたコードを以下に示します。 アルゴリズムは次のとおりです。
- 必要な次数degが1の場合、単純に1次の既約多項式の完成したリストを返します
- 必要な順序が1を超える場合：
- 次数degのすべての多項式を生成します（ Pをこれらの多項式のセットとします）
- 次の既約多項式のリストを見つける
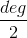（ Gをこれらの既約多項式の集合とする）
- 多項式の場合
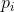多項式で割り切れない 
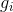、それは既約なので、追加する必要があります 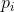結果のモジュール多項式のリストへ
object IrreduciblePolynomials{ private def check(p: Int, list: List[Int]): Boolean = { val pol = Polynomial(p) list.foreach((item: Int) => { val i = Polynomial(item) if ((pol div i)._2 == 0){ return false } }) true } def calcIrreducible(_deg: Int): List[Int] = { def calc(deg: Int): List[Int] = { if (deg == 1) return List[Int](2, 3)
完成した最終フィールドとなる具象FiniteField下位クラスを実装することは残っています。
class GaloisField(_initBitNumber: Int = FiniteField.DEFAULT_BIT_NUMBER) extends FiniteField(_initBitNumber) { override val modulo: Polynomial = ... protected def createModulo(): Option[Int] = { val list = IrreduciblePolynomials(this.bits) list.headOption } def createPolynomial(_initPolynomial: Int): GFPolynomial = { ... } def createPolynomial(_binInitPolynomial: String): GFPolynomial = { ... } class GFPolynomial private[GaloisField](_p: Int, _m: Int) extends FiniteFieldPolynomial with Comparable[GFPolynomial]{ override def equals(other: Any): Boolean = other match { case other: GFPolynomial => this.p.polynomial == other.p.polynomial case _ => false } override protected val p = Polynomial(_p) def this(other: GFPolynomial){ this(other.p.polynomial, bits) } override def self: GFPolynomial = this override def +(other: GFPolynomial): GFPolynomial = { GFPolynomial(this.p.polynomial ^ other.p.polynomial, bits) } override def -(other: GFPolynomial): GFPolynomial = {
乗算の結果はフィールドから「抜け出す」ことがあるため、結果をフィールドモジュールで除算する必要がある場合があります。 除算の実装方法に注意してください。これは、 aにbの乗法反転を乗算したものです。
反転は、 多項式クラスで定義された除算を使用して検出されます。
おわりに
その結果、ガロア体の自家製実装が可能になりました。これは、体の可能なサイズを大きくすることでさらに改善できます（ Intの代わりに、長い算術演算などを使用します）。
この記事は、学生や、抽象代数、分野、およびコーディング理論のトピックに興味のある人にとって有用です。
完全なアプリケーションコードはgithubにあります。