learnopengl。 レッスン1.7-変換

これで、オブジェクトの作成、色付け、テクスチャの適用方法がわかりましたが、それらは静的オブジェクトであるため、まだ退屈です。 各フレームの頂点の座標を変更することでそれらを移動させようとすることができますが、これはかなり面倒で、プロセッサの計算が必要です。 オブジェクトの変換を実行するはるかに便利な方法があります-これは行列を使用しています。 しかし、これはカンフーと人工デジタルの世界について話すことを意味するものではありません。

行列は非常に強力な数学的構造であり、最初は怖がりますが、慣れるとすぐに非常に便利になります。 行列について議論するときは、数学をもう少し深くする必要もあります。 また、より数学的な傾向のある読者のために、このトピックに関する追加リソースへのリンクを残します。

変換を完全に理解するには、まずベクトルを処理する必要があります。 この章の主なタスクは、後で必要になる基本的な数学的知識を提供することです。

ベクトル

最も単純な定義では、ベクトルは方向にすぎません。 ベクトルには方向と大きさ （モジュラスまたは長さとも呼ばれる）があります。 宝の地図上の方向としてベクトルを想像できます。「左に10歩、今度は北に3歩、右に5歩」。 この例では、「左」が方向であり、「10ステップ」がベクトルの長さです。 この宝の地図上の指示は、3つのベクトルで構成されています。 ベクトルは任意の次元を持つことができますが、2成分および4成分のベクトルが最もよく使用されます。 ベクトルが2成分の場合、平面（または2Dチャート）上の方向を表し、ベクトルが3成分の場合、3次元世界の方向を表します。

以下に3つのベクトルがあり、それぞれが2Dチャート上の矢印として（x、y）の形式で表されています。 （3Dよりも）2Dでベクトルを表現する方が直感的であるため、2Dベクトルは3Dベクトルと考えることができますが、Z座標はゼロです。 ベクトルが方向を表す限り、ベクトルの位置はその値を変更しません。 グラフでは、ベクトルvとwは同じですが、位置は異なります。

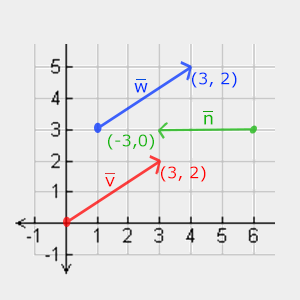
数学者がベクトルを記述するとき、彼らは上部に小さなダッシュを付けた小文字を使用することを好みます。 例：

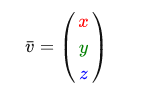
ベクトルは多くの場合方向を記述するため、それらを位置として想像するのは難しい場合があります。 通常、ベクトルを次のように視覚化します。中心を（0、0、0）に設定し、ポイントによって記述される方向を示します。 したがって、 位置ベクトルが取得されます（別のポイントを中心として、「このベクトルがこのポイントから空間内のポイントを指している」と言うこともできます）。 位置ベクトル（3、5 ）は、グラフ上の点（3、5）をベース（0、0 ）で指します。 ベクトルを使用して、2次元および3次元の空間で方向と位置の両方を記述することができます。

ベクトルに対していくつかの数学演算を実行することもできます。

スカラーベクトル演算

スカラーは単一の数値です（ベクトルを引き続き使用する場合は1成分のベクトル）。 スカラーによるベクトルの加算/減算/乗算または除算中に、単純にベクトルの各要素をこのスカラーで加算/減算/乗算または除算します。 例：

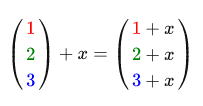
加算の代わりに、減算、乗算、または除算があります。

逆ベクトル

ベクトルの逆（否定）は、元の方向とは逆の方向のベクトルの受け取りです。 北東を指すベクトルの逆ベクトルは、南西を指すベクトルになります。 ベクトルを反転するには、単にベクトルに-1を掛けます。 例：

加算と減算

2つのベクトルの加算は、 コンポーネントごとに行われます 。 例：

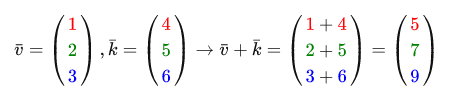
視覚的には、ベクトルv =（4,2）とk =（1,2）の合計は次のようになります。

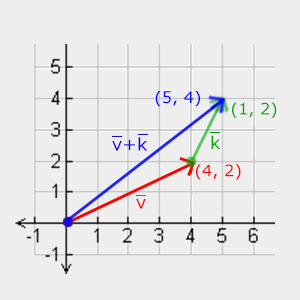
通常の加算および減算と同様に、ベクトルの減算も加算ですが、逆の2番目のベクトルでは：

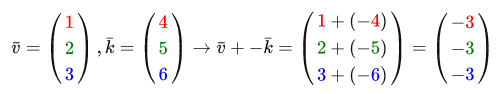
互いにベクトルを減算すると、オペランドの位置の差であるベクトルが生成されます。

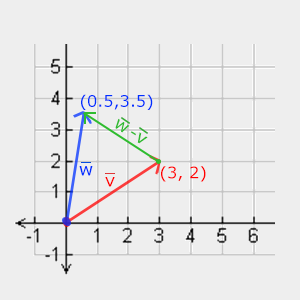
長さ

ベクトルの長さ（モジュール）を取得するには、 ピタゴラスの定理を使用します。これは、学校で覚えているかもしれません。 成分が三角形の辺として表される場合、ベクトルは三角形を形成します。

辺の長さ（x、y）がわかっていて、斜辺の長さを知りたいので、これを次のように行います。

どこ|| v || ベクトルvの長さです。 このような式は、 z ^ 2を追加することで3Dで簡単に拡張できます。 長さの計算例：

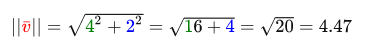
計算値：4.47

単位ベクトルと呼ばれる特別な種類のベクトルもあります。 このようなベクトルの特徴は、長さが常に1であることです。このベクトルをその長さで割ることにより、任意のベクトルをユニットに変換できます。

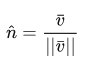
このようなベクトルは、 normalizedと呼ばれます。 単一のベクトルは、文字の上に小さな屋根で示されます。 また、このようなベクトルの方向のみを考慮する必要があるため、それらを使用する方が簡単です。

ベクトルとベクトルの乗算

2つのベクトルの乗算はかなり奇妙です。 通常の乗算​​は視覚的な意味を持たないため、適用できませんが、乗算中に選択できる2つの特定のアプローチがあります：最初は点として表されるスカラー積であり、2番目はクロスとして表されるベクトル積です。

スカラー積

2つのベクトルのスカラー積は、これらのベクトルの長さと、それらの間の角度のコサインを掛けたスカラー積に相当します。 この文が混乱している場合は、式を見てください：

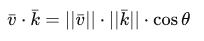
ベクトル間の角度はthetaとして記述されます。 なぜこれが面白いのでしょうか？ さて、ベクトルvとkが単位ベクトルであると想像してください。 したがって、式は次のようになります。

現在、スカラー積は2つのベクトル間の角度のみを決定します。 cos関数は90度の角度で0、角度0で1になることを覚えているかもしれません。これにより、ベクトルが互いに直交しているか、平行であるかを簡単に確認できます（直交性とは、ベクトルが長方形であることを意味します）。 sinまたはcosineについて詳しく知りたい場合は、基本的な三角法に関するKhan Academyのビデオをお勧めします。

また、2つの非単位ベクトル間の角度を計算することもできますが、そのためには、結果をこれらのベクトルの長さで割って、 cosのみを保持する必要があります。

それでは、スカラー積をどのように数えますか？ スカラー積は、ベクトルの成分の乗算とそれに続く結果の加算です。 例：

ベクトル間の角度を計算するには、この場合、余弦関数（cos ^ -1）を反転する必要があります-143.1度です。 したがって、これら2つのベクトル間の角度を効果的に計算しました。 スカラー作業は、光を扱うときに非常に便利です。

ベクターアートワーク

ベクトル積は3次元空間でのみ可能であり、2つの非平行ベクトルを入力として受け取り、入力に直交するベクトルを返します。 入力ベクトルが互いに直交している場合、ベクトル積は3つの直交ベクトルを作成します。 次に、これがなぜ役立つのかがわかります。 次の図は、3次元空間での外観を示しています。

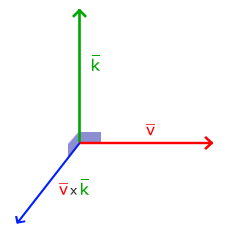
他の操作とは異なり、ベクトル積は線形代数に深く入り込まなければ直観的ではないため、式を覚えておいた方がよいでしょう。 以下は、2つの直交ベクトルAとBの間のベクトル積です。

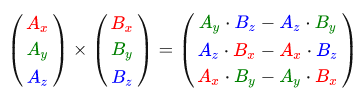
ご覧のとおり、この式はあまり意味がありません。 いずれにせよ、これらのすべてのステップの後、入力に直交するベクトルを受け取ります。

行列

さて、ベクトルに関するほとんどすべてを説明した後、マトリックスを詳しく調べます。 行列は通常、数字、文字、および/または式のセットからなる四角形です。 2x3マトリックスの例を次に示します。

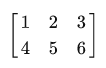
マトリックス要素は（i、j）を使用してアクセスされます。iは行で、jは列です。 これが、上記のマトリックスが2x3（3列2行）と呼ばれる理由です。 このようなシステムは、2Dグラフ（x、y）で使用されるシステムの逆です。 上記のマトリックスから値4を取得するには、インデックス（ 2、1 ） （2行目、1列目）を指定する必要があります。

実際、行列は数式の四角形の配列にすぎません。 また、数学プロパティの非常に優れたセットがあり、ベクトルのように、加算、減算、乗算などのいくつかの操作があります。

加算と減算

スカラーによる行列の追加は、次のように実行されます。

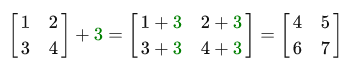
スカラーは、単純にマトリックスのすべての要素に追加されます。 引き算するときも同じことが起こります：

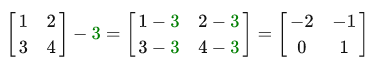
2つのマトリックス間の加算と減算は、要素ごとに実行されます。 したがって、加算および減算演算は、同じサイズの行列にのみ適用できます。 例：

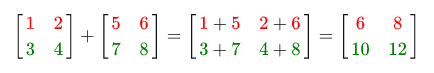
同じこと、減算のみ：

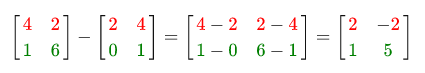
スカラー行列乗算

加算と減算に加えて、各行列要素にスカラーを乗算することにより、行列にスカラーが乗算されます。 例：

行列乗算

行列乗算はそれほど難しくありませんが、それほど単純でもありません。 乗算にはいくつかの制限があります。

1. 乗算できるのは、最初の列の列数が2番目の行列の行数と一致する行列のみです。
2. 行列の乗算は可換ではありません。 A * B！= B * A

2つの2x2行列を乗算する例を次に示します。

さて、多分あなたはここで何が起こっているのか理解しようとしていますか？ 行列の乗算は、通常の乗算​​と、左の行列の行と右の行列の列を使用した加算の組み合わせです。 次の図は、少し明確にする必要があります。

最初に、左のマトリックスの一番上の行と右のマトリックスの左の列を取得します。 私たちが選択した行と列は、結果のマトリックスのどの要素を計算するかを決定します。 左の行列の最初の行を取得した場合、結果の行列の一番上の行を操作し、次に右の行列の列を選択します。これにより、結果の行列のどの列を操作するかが決まります。 右下の要素を計算するには、左行列の一番下の行と右行列の右の列を選択する必要があります。

結果の値を計算するには、通常の乗算​​を使用して行と列の要素を乗算します。 その後、乗算結果が合計され、結果が得られます。 これが最初の制限の原因です。

結果はサイズ（n、m）の行列です。ここで、nは左の行列の行数、mは右の行列の列数です。

問題がある場合-心配しないでください。 手で計算を続け、困難が生じたときにこのレッスンに戻ります。 まもなく行列の乗算がオートマトンになります。

1つの大きな例で、行列乗算の問題を閉じましょう。 色は、アルゴリズムを表すために使用されます。 トレーニングのために、自分で結果を計算してから、例の結果と比較してみてください。

ご覧のとおり、行列の乗算は、多くのミスを犯す可能性のあるかなり厄介なプロセスです。 そして、これらの問題はサイズが大きくなるにつれて大きくなります。 それでも行列の数学的特性がもっと必要な場合は、 カーンアカデミーのビデオをお勧めします。

ベクトルによる行列乗算

過去のレッスンではすでにベクターを使用しました。 それらを使用して、位置、色、およびテクスチャ座標を表しました。 さて、ウサギの穴を少し深く見てみましょう。ベクトルは実際には単なるNx1行列であり、 Nはベクトル成分の数です。 少し考えてみれば、それは理にかなっています。 行列と同様に、ベクトルは数値の配列ですが、列は1つだけです。 そして、この情報はどのように役立ちますか？ マトリックスMxNがある場合、マトリックスの列数はベクトルの行数に等しいため、Nx1ベクトルで乗算できます。

しかし、なぜ行列にベクトルを掛けることができるのでしょうか？ マトリックスにベクトルを乗算して修正ベクトルを取得することにより、非常に多くの異なる3D / 2D変換を実行できます。 上記のテキストを完全に理解しているかどうかまだわからない場合は、次の例をご覧ください。

単位行列

OpenGLは通常、ほとんどのベクトルに4つの成分があるため、 4x4変換行列で動作します。 議論できる最も単純な変換行列は、 単位行列です。 単位行列は、ゼロで満たされたNxN行列ですが、対角線上に1があります。 ご覧のとおり、この行列はベクトルをまったく変更しません。

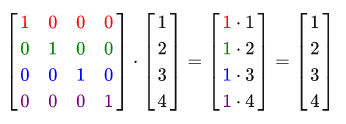
ベクトルは手つかずに見えます。 これは、乗算の規則から明らかになります。最初の結果の要素は、マトリックスの最初の行の各要素にベクトルの各要素を乗算したものです。 文字列の各要素は最初の要素を除いて0であるため、1 * 1 + 0 * 2 + 0 * 3 + 0 * 4 = 1になります。これは、ベクトルの残りの3要素にも適用されます。

あなたは、何も変換しない変換マトリックスがなぜ必要なのでしょうか？ 恒等行列は、多くの場合、他の変換行列を生成するための出発点であり、線形代数を掘り下げる場合、定理を証明し、線形方程式を解くための非常に便利な行列でもあります。

スケーリング行列

ベクトルをスケーリングする場合、矢印の長さをスケーリングの量だけ増やし、方向を維持します。 2次元または3次元で作業している間、2つか3つの量のベクトルによってスケーリングを決定できます。各ベクトルは、軸（x、yまたはz）の 1つをスケーリングします。

ベクトルv =（3,2）をスケーリングしてみましょう。 ベクトルをx軸に沿って0.5スケーリングします。これにより、ベクトルが2倍狭くなります。 y軸に沿って2でベクトルをスケーリングすると、高さが2倍になります。 ベクトルを（0.5、2）でスケーリングした場合の外観を見てみましょう。 結果をフォームsに書き込みます。

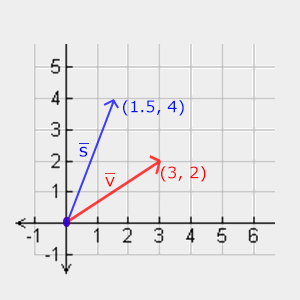
OpenGLは多くの場合3D空間で機能するため、2Dの場合はZ座標を1のままにしておくことができます。各軸のスケーリング値は異なるため、実行したスケーリング操作は異種です。 スケーリング値が同じ場合、そのような変換は均質と呼ばれます。

スケールアップする変換マトリックスを作成しましょう。 対角要素にベクトルの対応する要素が乗算されることは、単位行列で既に確認しました。 単位行列の単位をトリプルに置き換えるとどうなりますか？ この場合、ベクトルのすべての要素にこの値を掛けます。 したがって、スケーリング値を（S1、S2、S3）として表す場合、任意のベクトル（x、y、z）のスケーリング行列を決定できます。

ベクトルの4番目の要素は1であることに注意してください。このコンポーネントはwで示され、他のタスクに使用されます。

シフト行列

シフトは、1つのベクトルを別のベクトルに追加して、異なる位置の新しいベクトルを取得するプロセスです。つまり、 シフトベクトルに基づいたベクトルのシフトです。 ベクトルの追加についてはすでに説明しているため、これは新しいものではありません。
4x4マトリックスのスケーリングマトリックスと同様に、シフトに必要な操作を実行するためのいくつかの位置があります-これらは4番目の列の上位3つの要素です。 せん断ベクトルを（Tx、Ty、Tz）として表す場合、せん断行列を次のように定義できます。

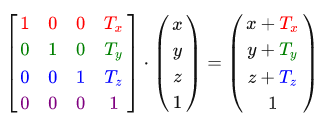
これは、すべてのベクトル値にベクトルのwコンポーネントが乗算され、初期値に追加されるため、機能します。 これは、3x3マトリックスを使用しては不可能です。

同次座標
ベクトルwの成分は同次座標 とも呼ばれます。 同次座標から3Dベクトルを取得するには、 x座標、 y座標、およびz座標をwで除算します。 ほとんどの場合、 wは1.0であるため、これは通常は気付きません。 同種座標の使用にはいくつかの利点があります：3Dベクトルのシフトを実行でき（ wコンポーネントがないとこれは不可能です）、次の章ではwの値を使用して3Dビジュアライゼーションを作成します。
また、同次座標が0の場合、成分wが0に等しいベクトルはシフトできないため、ベクトルは方向ベクトルと見なされます。

シフトマトリックスを使用すると、3方向（x、y、z）のすべてにオブジェクトを移動できるため、このマトリックスはタスクに非常に役立ちます。

回転行列

最後の2、3の変換は非常に理解しやすく、2Dまたは3D空間で表現できますが、回転にはもう少し注意が必要です。 これらの行列がどのように形成されるかを正確に知りたい場合は、 線形代数に関するカーンアカデミーのビデオをお勧めします。

まず、ベクトルの回転が何であるかを定義しましょう。 2Dおよび3Dの回転は、 角度によって決まります。 角度は、角度またはラジアンで表現できます。完全な回転は、それぞれ360度または2Piです。 学位は私にとってより論理的であるため、学位を扱うことを好みます。

ほとんどの回転関数はラジアン単位の角度を必要としますが、あるシステムから別のシステムに変換する利点は非常に簡単です。
度=ラジアン*（180.0f / PI）
ラジアン=度*（PI / 180.0f）
PIは約3.14159265359です

半円回転-360/2 = 180度の回転が必要です。 1/5を右に回転するには、360/5 = 72度右に回転する必要があります。 以下は、通常の2Dベクトルの例です 。vはkの右に72度回転します。

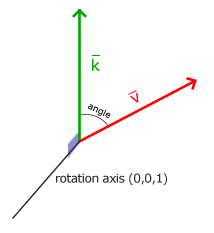
3Dでの回転は、角度と 回転軸によって記述されます。 角度は、この軸を中心にベクトルがどれだけ回転するかを決定します。 たとえば、3Dワールドで2Dベクトルを回転させる場合、回転軸-Zを設定します。

三角法を使用して、ベクトルを特定の角度で回転したものに変換できます。 これは通常、 sin関数とcos関数の巧妙な組み合わせで行われます。 変換行列がどのように生成されるかについての議論は、レッスンの範囲を超えています。

回転行列は3D空間の各軸に対して定義され、角度はthetaとして表示されます。
X軸の周りの回転行列：

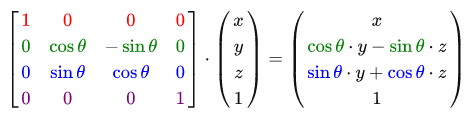
Y軸の周りの回転行列：

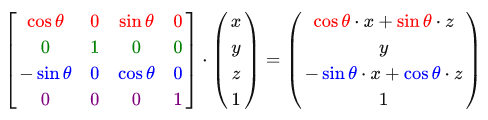
Z軸の周りの回転行列：

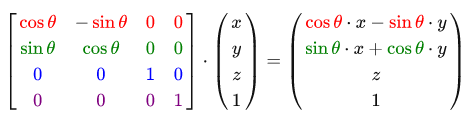
回転行列を使用して、3つの軸のいずれかに沿ってベクトルを回転できます。 たとえば、最初にX軸で回転させ、次にY軸で回転させるなど、これらを組み合わせると、ジンバルロック問題と呼ばれる問題がすぐに発生します。 詳細は説明しませんが、特定の軸の回転を組み合わせるのではなく、特定の軸の回転（たとえば（0.662、0.2、0.722） （これは単位ベクトルであることに注意）を使用することをお勧めします。 このような変換のマトリックスが存在し、次のようになります。ここで、（Rx、Ry、Rz）は回転軸です。

このようなマトリックスの生成に関する数学的な議論は、このレッスンの範囲外です。 そのようなマトリックスでさえ、ヒンジロックの問題を完全に解決するわけではないことを覚えておいてください（入手するのは簡単ではありません）。 この問題を完全に解決するには、四元数を使用して回転を処理する必要があります。四元数は、安全であるだけでなく、計算の点でもはるかに使いやすいです。 四元数の議論は後のレッスンのために留保されているかもしれません。

マトリックスの組み合わせ

変換にマトリックスを使用する最大限の有用性を実現するには、変換マトリックスを1つのマトリックスに結合する必要があります。 いくつかの変換を含む変換マトリックスを生成できるかどうかを見てみましょう。 たとえば、ベクトル（x、y、z）があり、それを2倍にスケーリングして（1、2、3）だけシフトしたいとします。 これを行うには、スケーリング行列と変位行列が必要です。 その結果、次のような結果が得られます。

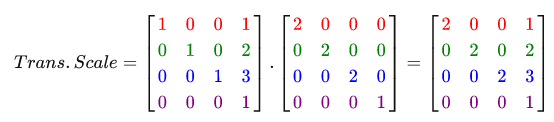
行列の乗算中に、最初にシフトしてからスケーリングすることに注意してください。 行列の乗算は可換ではありません。つまり、乗算の順序が重要です。 行列の乗算では、右の行列にベクトルが乗算されるため、乗算を右から左に読む必要があります。 行列の結合中に、スケーリングを開始し、次に回転し、最後にシフトすることをお勧めします。そうしないと、互いに否定する可能性があります。 たとえば、最初にシフトを実行してからスケーリングを実行すると、シフトマトリックスもスケーリングされます。

その結果、変換マトリックスは次のように適用されます。

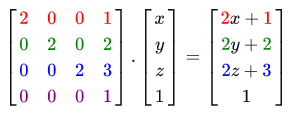
さて、ベクトルは2倍にスケーリングされ、 （1、2、3）だけシフトされます。

実際に

理論全体について議論した後、それを実践に移します。 OpenGLにはマトリックスまたはベクトル変換のサポートが組み込まれていないため、独自の数学クラスと関数を使用する必要があります。 これらのレッスンでは、微妙な数学的詳細から抽象化し、既製の数学的ライブラリを使用します。 幸いなことに、GLMと呼ばれるOpenGL数学ライブラリの下に、使いやすく鋭利なものが既にあります。

GLM

GLMは、Open GL M athematicsの頭字語です。 このライブラリはヘッダーです。つまり、必要なヘッダーファイルを含めるだけで十分です。 リンクやコンパイルを気にする必要はありません。 GLMは、 公式Webサイトからダウンロードできます。 ヘッダーファイルを含むルートディレクトリをincludeフォルダーにコピーすると、起動できます。

ほとんどのGLM機能は、3つのヘッダーファイルにあります。

#include <glm/glm.hpp> #include <glm/gtc/matrix_transform.hpp> #include <glm/gtc/type_ptr.hpp> 

変換に知識を適用して、ベクトル（ 1、0、0 ）を （ 1、1、0 ）だけシフトできるかどうかを見てみましょう（ glm :: vec4から1.0に等しい同次座標を指定したことに注意してください）：

 glm::vec4 vec(1.0f, 0.0f, 0.0f, 1.0f); glm::mat4 trans; trans = glm::translate(trans, glm::vec3(1.0f, 1.0f, 0.0f)); vec = trans * vec; std::cout << vec.x << vec.y << vec.z << std::endl; 

最初に、GLM組み込みベクトルクラスを使用して、 vecというベクトルを作成しました。 次に、4x4単位行列であるmat4を定義します。 次に、単位行列をシフトベクトルと共にglm :: translate関数に渡すことにより、変換行列を作成します。
次に、ベクトルに変換行列を掛けて結果を出力します。 シフト行列がどのように機能するかをまだ覚えている場合、結果のベクトルは（1 + 1、0 + 1、0 + 0）である必要があることを理解します。これは（2、1、0）です。 上記のコードは210を出力します。これは、シフトマトリックスがジョブを実行したことを意味します。

もっと面白いことをしてスケールを試みてから、最後のレッスンのオブジェクトを回転させましょう。 最初に、コンテナを反時計回りに90度回転します。 次に、2倍に縮小するために0.5でスケーリングします。 このための変換マトリックスを作成しましょう。

 glm::mat4 trans; trans = glm::rotate(trans, 90.0f, glm::vec3(0.0, 0.0, 1.0)); trans = glm::scale(trans, glm::vec3(0.5, 0.5, 0.5)); 

最初に、各軸でコンテナを0.5ずつ縮小し、コンテナをZ座標で90度回転します。 テクスチャも回転していることに注意してください。 マトリックスを各GLM関数に渡すため、GLMは自動的にマトリックスを乗算し、変換マトリックスを生成します。

GLMの一部のバージョンは、角度ではなくラジアン単位の角度を受け入れます。 そのようなバージョンがある場合は、 glm :: radians（90.0f）を使用して度をラジアンに変換します。

次の大きな問題は、変換マトリックスをシェーダーに転送する方法です。 GLSLのタイプはmat4であると先に述べました。 したがって、 mat4を一様な変数として使用し、位置ベクトルにこの行列を掛けることは残ります。

 #version 330 core layout (location = 0) in vec3 position; layout (location = 1) in vec3 color; layout (location = 2) in vec2 texCoord; out vec3 ourColor; out vec2 TexCoord; uniform mat4 transform; void main() { gl_Position = transform * vec4(position, 1.0f); ourColor = color; TexCoord = vec2(texCoord.x, 1.0 - texCoord.y); } 

GLSLには、ベクターと同じ操作を提供するmat2およびmat3タイプもあります。 この記事に記載されているすべての操作は、マトリックスタイプで利用できます。

gl_Positionに渡す前に、ユニフォームを追加し、位置ベクトルに変換行列を乗算しました 。 コンテナは2倍小さくなり、90度回転します。 しかし、まだ変換マトリックスをシェーダーに渡す必要がありますか？

 GLuint transformLoc = glGetUniformLocation(ourShader.Program, "transform"); glUniformMatrix4fv(transformLoc, 1, GL_FALSE, glm::value_ptr(trans)); 

まず、変数の均一な位置を取得し、 Matrix4fv後置記号付きのglUniform関数を使用して変数に行列データを送信します。 最初の引数は変数の位置でなければなりません。 2番目の引数は、OpenGLに送信するマトリックスの数、この場合は1を指示します。3番目の引数は、マトリックスを転置するかどうかを指定します。 OpenGL開発者は、列優先順序と呼ばれる内部マトリックス形式をよく使用します。これは、GLMでデフォルトで使用されるため、マトリックスを転置する必要はありません。GL_FALSEのままにしておくことができます。 実際、最後のパラメーターはデータですが、GLMはOpenGLが見たいデータを正確に保存しないため、 value_ptrを使用して変換します 。

変換マトリックスを作成し、頂点シェーダーで均一と宣言し、シェーダーでマトリックスを送信して、頂点座標を修正しました。 結果は次のようになります。

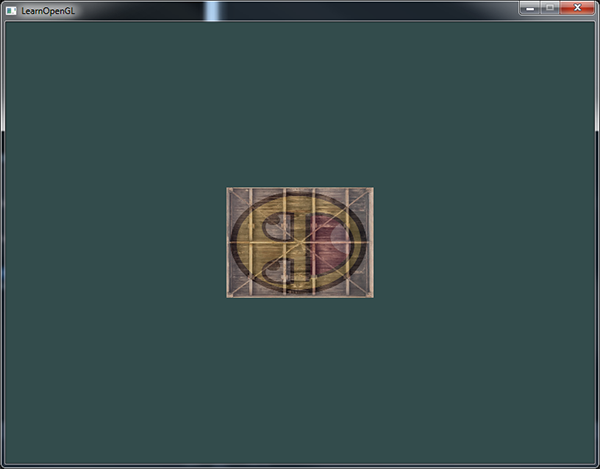
いいね！ コンテナは本当に左に曲がり、2倍小さくなったため、変換は成功しました。 コンテナをリアルタイムで回転させ、右下隅に移動させましょう。 これを行うには、メインループの各反復で計算を実行する必要があります。 GLFW関数を使用して、時間とともに角度を変更する時間を取得します。

 glm::mat4 trans; trans = glm::translate(trans, glm::vec3(0.5f, -0.5f, 0.0f)); trans = glm::rotate(trans,(GLfloat)glfwGetTime() * 50.0f, glm::vec3(0.0f, 0.0f, 1.0f)); 

どこでも変換行列を宣言する前に、各フレームの回転を更新できるように各反復で作成することに注意してください。 つまり、ゲームループの各反復で変換行列を再作成する必要があります。 通常、シーンに複数のオブジェクトがある場合、レンダリングの各反復で新しい値を使用してそれらの変換行列が再作成されます。

次に、オブジェクトを中心（0、0、0）の周りに回転させ、その後、回転させたバージョンを画面の右下隅に移動します。 変換を適用する実際のシーケンスは逆の順序で読み取られることを忘れないでください。コードでも、最初にシフトしてから回転すると、変換は逆の順序、最初、ターン、シフトの順に適用されます。 これらのすべての変換と、それらがオブジェクトにどのように影響するかを理解することはかなり困難です。 変換を試してみると、すぐに慣れます。

すべてを正しく行った場合、次のようになります。

以上です。 時間の経過とともに回転するシフトされたコンテナー。これはすべて、単一の変換マトリックスで行われます。 これで、グラフィックスの世界でマトリックスが非常に強い理由を確認できます。 変換を無制限に定義し、それらを1つのマトリックスに結合して、後で再利用できます。 頂点シェーダーでこのような変換を使用すると、データをバッファーに送信する必要がないため、頂点データを変更しないでプロセッサ時間を節約できます。

正しい結果が得られなかった場合、またはどこかに行き詰まっている場合は、 頂点シェーダーとフラグメントシェーダーと共にソースコードを確認してください。

次のレッスンでは、マトリックスを使用して頂点のさまざまな座標空間を定義する方法について説明します。 これは、リアルタイムの3Dグラフィックスの世界における新しいステップです！

演習

• 最後の変換でアクションのシーケンスを変更し、何が起こるかを見て、結果がまさにそれである理由を正当化しようとします。 解決策
• glDrawElementsを呼び出して別のコンテナを描画してみてください。ただし、このコンテナを別の場所に別の変換で配置してください。 右上隅に配置し、回転ではなく、サイズを変更します（ここではsin関数を使用できます）。