よくある間違い初心者は画像を操作します

デジタル画像処理は非常に興味深い分野ですが、初心者が常に遭遇する落とし穴がたくさんあります。 私たちは学生を助成金やプロジェクトに積極的に引き付けますが、新しい画像処理アルゴリズムの実装を必要とする実際のタスクを学生に与えようとすると、子供たちの間違いに恐怖を覚えました。

したがって、本格的なタスクを設定する前に、学生に標準的な画像処理アルゴリズムを実装するためのいくつかの実用的なタスクを提供し始めました：画像の基本操作（回転、ぼかし）、畳み込み、単純なフィルターを使用した補間（双線形、双三次）、方向補間、アルゴリズムを使用した境界抽出キャニー、キーポイント検出など プログラミング言語はどれでもかまいませんが、タスクの実行時には、画像の読み取りと書き込みを除き、サードパーティのライブラリを使用することはできません。 これは、タスクが本質的に教育的であり、アルゴリズムの独立した実装がプログラミングの優れた実践であり、メソッドが内部からどのように機能するかを理解できるという事実によるものです。

この記事では、学生が画像処理で実際的なタスクを実行するときに犯す最も一般的な間違いについて説明します。 画像は普通のもので、16ビットの色深度、パンクロマティック性、3D画像のエキゾチックなタイプはありません。

エラー1.システムオブジェクトBitmap、HBITMAPなどを使用して画像を保存するためにピクセルを操作する

これらのオブジェクトは、グラフィックスサブシステムと相互作用するように設計され（プリミティブとテキストの描画、画面への表示）、画像ピクセルが保存されているメモリ領域への直接アクセスを提供しません。 ピクセルには、GetPixelおよびSetPixel関数を使用してアクセスします。 これらの関数の呼び出しは非常に高価です-ピクセルへの直接アクセスよりも2〜3桁遅くなります。 誘惑は、ビットマップタイプがすぐに利用できるC＃で特に優れています。

解決策：これらのクラスは、ファイルからの読み取り、ファイルへの書き込み、画面への表示にのみ使用し、他の場合は、ピクセルに効果的にアクセスできるクラスを操作します。

注：場合によっては、WindowsでDIB（デバイスに依存しないビットマップ）を使用すると便利です。ピクセルに直接アクセスでき、画面に表示できます。マイナスはピクセルの種類の制限です。

エラー2.画像処理の経験がなくても画像を操作するためにライブラリを使用する

ライブラリの使用には、アルゴリズムの操作に関する理解不足と、ライブラリにない独自のアルゴリズムの開発を必要とする実際的な問題を解決する際のさらなる困難が伴います。 たたみ込みなどの基本的な操作すら実装できないプログラミングの優れた学生に出会いました。ライブラリを接続できなかったか、そのように機能しませんでしたが、10行の関数を記述するだけの心がありませんでした。

解決策：サードパーティのライブラリを使用せずに、画像を操作するための独自のクラスを作成し、基本的なアルゴリズムを独自に実装します。 これは、十分なプログラミング経験がない人にとって特に便利です。 愚かなミスのためにプロジェクト全体を埋め尽くすよりも、自転車を数回壊した方が良いでしょう。

間違い3.丸めの精度が失われます。

さまざまな画像処理アルゴリズムを適用した結果、実際のタイプの中間結果が生じます。 例：ほとんどすべての平均化フィルター、たとえばガウスフィルター。 結果をバイト型にキャストすると、追加のエラーが発生し、アルゴリズムの精度が低下します。

以下に、Cannyパス検出アルゴリズムの動作の例を示します。そのコンポーネントの1つは、勾配モジュラスの計算です。 左側-計算後の勾配モジュールはfloat型に格納され、右側-バイトに丸められます。

丸みを付けると、輪郭が破れることがわかります。

解決策：アルゴリズムの精度が重要な場合は、バイトの代わりにフロートタイプを使用してピクセル値を保存し、時期尚早な最適化を行わないでください-最初にアルゴリズムをフロートで正常に動作させてから、品質が低下しないようにバイトを使用できる場所を検討してください

注：実数を使用する最新のプロセッサーの速度は整数に匹敵します。 場合によっては、コンパイラは自動ベクトル化を適用できます。これにより、floatを使用したコードが高速化されます。 また、多数のバイトフロート変換、丸め、クリッピングを使用すると、フロートを含むコードが高速になることがあります。 しかし、doubleの使用が正当化されることはめったになく、floatとdoubleからのハッシュは、一般に、それらを使用するタイプと原則の誤解の結果です。

整数型（byte、int16、uint16）を使用することは、メモリアクセス速度がボトルネックになるベクトル演算を使用する場合に特に効果的です。

エラー4.範囲[0、255]の範囲外のピクセル値

精度に問題はありませんが、バイト値を使用してピクセル値を保存したいですか？ その後、別の問題が発生します。バイキュービック補間やシャープニングなどの多くの操作により、指定された範囲外の値が表示されます。 この事実を考慮しない場合、折り返しと呼ばれる効果が発生します。値260は4に、–3は253に変わります。明るい背景に明るい点と線が表示され、明るい背景に暗い点と線が表示されます（左側-正しい実装、右側-エラーあり） 。

解決策：中間操作を実行する場合、各ステップで可能な値の範囲を確認し、バイト型に変換する場合、範囲が範囲外であることを確認する必要があります。たとえば、次のようになります。

unsigned char clamp(float x) { return x < 0.0f ? 0 : (x > 255.0f ? 255 : (unsigned char)x); } 

エラー5。範囲[0、255]へのキャストの結果としての値の損失

タイプバイトで作業し、 clamp機能を使用したいですか？ 丸めの場合のように、何も失うことはありませんか？

実際に、微分を計算するとき、またはソーベルフィルターを適用するとき、生徒が負の値を失う方法を見ました。

解決策：中間結果を保存するのに十分なサイズのタイプを使用し、クランプ機能はファイルまたはディスプレイに保存するためだけに使用します。 導関数を視覚化するには、ピクセル値に128を追加するか、モジュールを使用します。

エラー6.不正なピクセルバイパス順序。プログラムの速度が低下します

コンピューターのメモリは1次元です。 2次元画像は、1次元配列としてメモリに保存されます。 通常、それらは行ごとに書き込まれます。最初は0番目の行、次に1番目が続きます。
順次メモリアクセスは、ランダムアクセスよりも高速です。 これは、メモリからのデータを大きなブロックでキャッシュに入れるプロセッサキャッシュが原因です。たとえば、最新のプロセッサでは64バイトです。 いくつかの水平方向に隣接するピクセルが一度にこのブロックに入ります。 つまり、同じ行の後続のピクセルにアクセスする場合、アクセス速度は列の後続のピクセルよりも速くなります。

解決策：メモリアクセスがシーケンシャルになるように、イメージのバイパスを行う必要があります。外側のループ、垂直バイパス、および内側のループで水平に：

 for (int y = 0; y < image.Height(); y++) for (int x = 0; x < image.Width(); x++) ... 

注：異なる言語では、メモリ内の多次元配列の表現方法が異なる場合があります。 これを覚えておいてください。

間違い7.幅と高さの混乱

古典的な問題：テストは存在しないか、正方形の画像でのみ実行されます;フィールドでは、長方形の画像を操作する場合、配列は境界を越えます。

解決策：テストを忘れないでください！ 私はTDDについての議論を育てないことを提案します：TDDの使用は皆の個人的なビジネスです。

間違い8.抽象化の拒否

エンティティを作成することへの恐怖は初心者の典型的な間違いであり、コードの可読性と認識に関する問題につながります。 ここに多くの例を挙げることができます。

1. getPixel(x, y)およびsetPixel(x, y)メソッドを使用する代わりに、配列内のインデックスを直接計算してピクセルにgetPixel(x, y)ます。 利便性に加えて、これらの方法では、画像の境界を超えて出力をチェックし、正しく処理することができます。 たとえば、エラーを与えないで、画像値を外挿します。

 b1 = (float)0.25 * ( w1 - 1) * (w1 - 2) * (w1 + 1) * (h1 - 1) * (h1 - 2) * (h1 + 1); b2 = -(float)0.25 * w1 * (w1 + 1) * (w1 - 2) * (h1 - 1) * (h1 - 2) * (h1 + 1); b3 = -(float)0.25 * (w1 - 1) * (w1 - 2) * (w1 + 1) * (h1 + 1) * (h1 - 2); b4 = (float)0.25 * w1 * h1 * (w1 + 1) * (w1 - 2) * (h1 + 1) * (h1 - 2); b5 = -(1 / 12) * w1 * (w1 - 1) * (w1 - 2) * (h1 - 1) * (h1 - 2) * (h1 + 1); b6 = -(1 / 12) * h1 * (w1- 1) * (w1 - 2) * (w1 + 1) * (h1 - 1) * (h1 - 2); b7 = (1 / 12) * w1 * h1 * (w1 + 1) * (w1 - 2) * (h1 + 1) * (h1 - 2); b8 = (1 / 12) * w1 * h1 * (w1- 1) * (w1 - 2) * (h1 - 1) *( h1 - 2); b9 = (1 / 12) * w1 * (w1 - 1) * (w1 + 1) * (h1 - 1) * (h1 - 2) * (h1 + 1); b10 = (1 / 12) * w1 * (w1 - 1) * (w1 - 2) * (w1 + 1) * (h1 - 1) * (h1+ 1); b11 = (1 / 36) * w1 * h1 * (w1 - 1) * (w1 - 2) * (w1 - 1) * (h1 - 2) * (h1- 2); b12 = -(1 / 12) * w1 * h1 * (w1 - 1) * (w1 + 1) * (h1 + 1) * (h1 - 2); b13 = -(1 / 12) * w1 * h1 * (w1 + 1) * (w1 - 2) * (h1 - 1) * (h1 + 1); b14 = -(1 / 36) * w1 * (w1 - 1) * (w1 + 1) * (h1 - 1) * (h1 - 2); b15 = -(1 / 36) * w1 * h1 * (w1 - 1) * (w1 - 2) * (h1 - 1) * (h1 + 1); b16 = (1 / 36) * w1 * h1 * (w1 - 1) * (w1 + 1) * (h1 - 1) * (h1 + 1); image2.rawdata[y1 * image2.Width + x1].b = image1.rawdata[h * image1.Width + w].b * b1 + image1.rawdata[h * image1.Width + w + 1].b * b2 + image1.rawdata[(h + 1) * image1.Width + w].b * b3 + image1.rawdata[(h + 1) * image1.Width + w + 1].b * b4 + image1.rawdata[h * image1.Width + w - 1].b * b5 + image1.rawdata[(h - 1) * image1.Width + w].b * b6 + image1.rawdata[(h + 1) * image1.Width + w - 1].b * b7 + image1.rawdata[(h - 1) * image1.Width + w + 1].b * b8 + image1.rawdata[h * image.Width + w + 2].b * b9 + image1.rawdata[(h + 2) * image1.Width + w].b * b10 + image1.rawdata[(h - 1) * image1.Width + w - 1].b * b11 + image1.rawdata[(h + 1) * image1.Width + w + 2].b * b12 + image1.rawdata[(h + 2) * image1.Width + w + 1].b * b13 + image1.rawdata[(h - 1) * image1.Width + w + 2].b * b14 + image1.rawdata[(h + 2) * image1.Width + w - 1].b * b15 + image1.rawdata[(h + 2) * image1.Width + w + 2].b * b16; image2.rawdata[y1 * image2.Width + x1].g = image1.rawdata[h * image1.Width + w].g * b1 + image1.rawdata[h * image1.Width + w + 1].g * b2 + image1.rawdata[(h + 1) * image1.Width + w].g * b3 + image1.rawdata[(h + 1) * image1.Width + w + 1].g * b4 + image1.rawdata[h * image1.Width + w - 1].g * b5 + image1.rawdata[(h - 1) * image1.Width + w].g * b6 + image1.rawdata[(h + 1) * image1.Width + w - 1].g * b7 + image1.rawdata[(h - 1) * image1.Width + w + 1].g * b8 + image1.rawdata[h * image1.Width + w + 2].g * b9 + image1.rawdata[(h + 2) * image1.Width + w].g * b10 + image1.rawdata[(h - 1) * image1.Width + w - 1].g * b11 + image1.rawdata[(h + 1) * image1.Width + w + 2].g * b12 + image1.rawdata[(h + 2) * image1.Width + w + 1].g * b13 + image1.rawdata[(h - 1) * image1.Width + w + 2].g * b14 + image1.rawdata[(h + 2) * image1.Width + w - 1].g * b15 + image1.rawdata[(h + 2) * image1.Width + w + 2].g * b16; image2.rawdata[y1 * image2.Width + x1].r = image1.rawdata[h * image1.Width + w].r * b1 + image1.rawdata[h * image1.Width + w + 1].r * b2 + image1.rawdata[(h + 1) * image1.Width + w].r * b3 + image1.rawdata[(h + 1) * image1.Width + w + 1].r * b4 + image1.rawdata[h * image1.Width + w - 1].r * b5 + image1.rawdata[(h - 1) * image1.Width + w].r * b6 + image1.rawdata[(h + 1) * image1.Width + w - 1].r * b7 + image1.rawdata[(h - 1) * image1.Width + w + 1].r * b8 + image1.rawdata[h * image1.Width + w + 2].r * b9 + image1.rawdata[(h + 2) * image1.Width + w].r * b10 + image1.rawdata[(h - 1) * image1.Width + w - 1].r * b11 + image1.rawdata[(h + 1) * image1.Width + w + 2].r * b12 + image1.rawdata[(h + 2) * image1.Width + w + 1].r * b13 + image1.rawdata[(h - 1) * image1.Width + w + 2].r * b14 + image1.rawdata[(h + 2) * image1.Width + w - 1].r * b15 + image1.rawdata[(h + 2) * image1.Width + w + 2].r * b16; 

2.カラー画像を操作する際のコードの重複により、エラーが発生します（上記の例を参照）。 コードをコピーして貼り付け、 rをgとb置き換える代わりに、演算子のオーバーロードを使用するだけで十分です。 コードが3倍少なく、3倍明確です。

3.画像用に個別のクラスを作成する代わりに、2次元配列を使用します。
問題は、インデックス付けが不自然- (y, x) (x, y) (y, x)ではなく(y, x)であり、配列の次元が明確ではないことです： GetLength(0)とGetLength(1)から幅があること、および高さがあることは明らかではありません。 インデックスを単純に混乱させるリスクが高くなります。

4.画像用に個別のクラスを作成する代わりに、カラー画像を保存するための3次元配列の使用。 前の段落に加えて、どのインデックスがどの色成分に対応するかを覚えておく必要があります。 また、3次元配列が(vx, vy)の形式と(v, angle)の形式の両方でベクトルを格納するためにどのように使用されるかを見ました。 混乱するのは簡単です。

5.クラスの代わりに配列を使用します。 次の関数が返すものを推測しますか？

 public static double[] HoughTransform2(GrayscaleFloatImage image, ref float[][] direction, ColorFloatImage cimage) 

回答：11個の要素の配列。各要素には独自の神聖な意味があり、コードを長時間分析しなければ理解できない。 それをしないでください！ クラスを取得し、各フィールドに人間の名前を付けます。

6.セマンティクスの変更を伴う変数の再利用。 コードにgradxとgradyがあり、 xとy生産的だと思いますか？ そしてここにあります、これはモジュールと角度です：

 gradx[x, y] = (float)Math.Sqrt(temp1 * temp1 + temp2 * temp2); grady[x, y] = (float)(Math.Abs(Math.Atan2(temp2, temp1)) * 180 / Math.PI); 

解決策：魔法の定数とインデックスはありません。 画像を個別のクラスとして設計し、ピクセル自体も入力する必要があり、ピクセルへのアクセスは特別な方法のみで行う必要があります。

間違い9.一部の数学関数の適用が正しくない、または場違いである

これは、プロセッサアーキテクチャ、一連の命令、およびそれらの実行にかかる時間に関する理解が不十分であるためです。 許されて、経験がありますが、私が注意するいくつかのポイント：

1. x * x代わりにMath.Pow(x, 2)またはpow(x, 2)の形式で二乗します。
コンパイラーはこれらの構成を最適化しません。シングルサイクル乗算の代わりに、指数と対数の計算を含むかなり複雑なコードを生成し、1桁または2桁の速度低下につながります。

2.整数部分を(int)Math.Floor((float)(j) / k)として、 kは実数でループ内で変化しません。

ここでは、 (int)(j / k) 、さらに良い(int)(j * inv_k) float inv_k = 1.0f / k (int)(j / k)と記述するだけで十分です。

実際、floorは実数を返すため、さらに実数を整数に変換する必要があります。 それは非常に高価な余分な操作であることがわかります。 乗算による除算の置き換えは最適化にすぎず、除算操作は依然として高価です。

3.戻り値の計算。

 double _sum = pow(sum, -1); 

_sum = 1.0 / sum?書くことができる_sum = 1.0 / sum? 、なぜこれを行うの_sum = 1.0 / sum?

解決策：数学関数は必要な場合にのみ使用してください。

間違い10.言語の無知

そして再び、数学の問題：

1.型との混同。 int代わりにピクセルインデックスにlong longを使用し、 float 、 double 、およびint間の定数変換を行います。 たとえば、なぜ1.0f / 16.0f書くことができるのに(float)(1.0 / 16)書くのでしょうか？

2. atanを使用した大騒ぎによる極角の計算と、必要なことを正確に行うatan2を使用する代わりにゼロで除算する問題。

3.異常な指数と魔法の定数：

 g=(float)Math.pow(2.71,-(d*d)/(2*sigma*sigma)); t=((float)1/((float)Math.sqrt(6.28)*sigma)); 

ここでは、学生は単にexp関数と定数piの存在を忘れていました。 (float)1代わりに、単に1.0fと書くことができます。

解決策：より多くのプログラムを作成し、この方法でのみ経験を積んでください。

エラー11.コードの難読化

初心者のプログラマーは、理解しやすいというよりも短いコードを書くことを好み、自分のスキルを示すのを好みます。

1.複雑なサイクル

 for (int x1 = x - 1, x2 = 0; x1 <= x + 1; x1++, x2++) { for (int y1 = y - 1, y2 = 0; y1 <= y + 1; y1++, y2++) { 

ここでは、-1から1までのサイクルを作成し、サイクル内で既にx1とx2を計算し、順序を変更するのが正しいでしょう。

 for (int j = -1; j <= 1; j++) { int y1 = y + j, y2 = j + 1; for (int i = -1; i <= 1; i++) { int x1 = x + i, x2 = i + 1; 

コンパイラーは単純なループを簡単に最適化できるため、さらに高速になります。

2.クールな機能

 long long ksize = llround(fma(ceil(3 * sigma), 2, 1)), rad = ksize >> 1; 

そして普通の人はただ書く

 int rad = (int)(3.0f * sigma); int ksize = 2 * rad + 1; 

そして、これは一般的に善悪を超えています。

 kernel[idx] = exp(ldexp(-pow(_sigma * (rad - idx), 2), -1)); 

理解していない人のために： ldexp(x, -1)は2による除算です。

解決策：遅かれ早かれ、そのようなコードのためにハンマーで指を打つことを覚えておいてください。

エラー12.処理された画像の値の破損

以下に、Cannyアルゴリズムの一部である非最大値を抑制するコードを示します。

 for x in xrange(grad.shape[0]): for y in xrange(grad.shape[1]): if ((angle[x, y] == 0) and ((grad[x, y] <= grad[getinds(grad, x + 1, y)]) or (grad[x, y] <= grad[getinds(grad, x - 1, y)]))) or\ ((angle[x, y] == 0.25) and ((grad[x, y] <= grad[getinds(grad, x + 1, y + 1)]) or (grad[x, y] <= grad[getinds(grad, x - 1, y - 1)]))) or\ ((angle[x, y] == 0.5) and ((grad[x, y] <= grad[getinds(grad, x, y + 1)]) or (grad[x, y] <= grad[getinds(grad, x, y - 1)]))) or\ ((angle[x, y] == 0.75) and ((grad[x, y] <= grad[getinds(grad, x + 1, y - 1)]) or (grad[x, y] <= grad[getinds(grad, x - 1, y + 1)]))): grad[x, y] = 0 

ここで、いくつかの値はgrad[x, y] = 0消失し、サイクルの後続の反復でアクセスされます。 中間結果を計算するために新しいイメージが作成され、現在のイメージが上書きされなかった場合、エラーは発生しませんでした。

解決策：事前にメモリを節約しようとせず、機能的なパラダイムについて考えてください。

その他のエラー

残りのエラーは、本質的に既に非プログラム的です。 これらは、誤解によるアルゴリズムの実装のエラーであり、個別のものです。 たとえば、ガウスフィルターのカーネルサイズの誤った選択。

ガウスフィルターは、画像処理の主要なフィルターの1つです。 エッジとリッジの検出、キーポイントの検索、シャープニングなど、膨大な数のアルゴリズムの基礎になっています。 ガウスフィルターには、ぼかしのレベルを決定するシグマパラメーターがあり、そのコアは次の式で表されます。

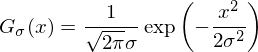
グラフの形式は次のとおりです。

この関数は決して消滅せず、無限サイズのカーネルとの畳み込みは意味をなしません。 したがって、エラーが無視できるようにカーネルサイズが選択されます。 実際のタスクでは、半径が(int)(3 * sigma)カーネルを取るだけで十分です。エラーは1/1000未満になります。 小さすぎるカーネル（上のグラフの赤い関数）を選択すると、ガウスフィルターが歪みます。 固定サイズのカーネル（5x5など）を使用すると、 sigma = 1.5でも誤った結果になります。

結論：初心者が画像を操作するための一般的なガイドライン

1. システムオブジェクトBitmap、HBITMAPなどを使用しないでください。
2. 画像を操作するためにライブラリを使用する前に、自転車を書くことから始めて、それから戦いに突入してください。
3. 精度と範囲の両方でピクセル値を格納するにはバイト型では不十分な場合、ピクセル値を格納するにはfloat型を使用します。 また、経験を積むことで、固定小数点演算を使用して最大の効率を達成できます。
4. 浮動小数点からバイトに変換するときは、丸め誤差と型境界を超えることに注意してください。
5. 負の値に注意してください。
6. 画像内のピクセルを正しい順序で走査します。
7. コードを慎重にテストします。
8. エンティティを生成することを恐れないでください。 コードは明確でなければなりません。
9. 数学演算を賢く使用してください。
10. 言語を学ぶ。
11. スキルを見せようとしないでください。
12. 画像処理のチュートリアルを読んでください-彼らは多くの有用なものを書きます。

プログラムの作成を容易にするために、画像の読み取りと書き込みが既に実装されているプロジェクトを作成し、最小限の機能で画像を保存するためのクラスを作成し、画像に対する操作の例を示しました。

→ Visual Studio 2015、C ++
→ Visual Studio 2015、C＃

Linuxのバージョンはありません。Linuxを使用している学生は、通常、このような問題を経験しません。

まあ、おやつ-ちょうど写真。

Cannyアルゴリズムを使用した回線抽出。 左上の入力画像があり、左の2番目が正しい結果であり、残りは誤った結果です。

バイキュービック補間を使用した倍率。