六角形ネット(六角形ネット)は一部のゲームで使用されていますが、長方形のネットほど単純で一般的ではありません。 私はほぼ20年間
六角形のグリッドで
リソースを収集してきましたが、このガイドは最も単純なコードで実装された最もエレガントなアプローチについて書いています。 Charles FuとClark Verbruggeのガイドは、記事全体でよく使用されます。 六角形グリッドを作成するさまざまな方法、それらの関係、および最も一般的なアルゴリズムについて説明します。 この記事の多くの部分はインタラクティブです。グリッドのタイプを選択すると、対応するパターン、コード、テキストが変更されます。
(注レーン:これはオリジナルにのみ適用されます。勉強することをお勧めします。翻訳では、オリジナルのすべての情報が保存されますが、対話性はありません。)この記事のコード例は疑似コードで書かれているため、実装を作成するために読みやすく、理解しやすいです。
幾何学
六角形は六角形の多角形です。 通常の六角形では、すべての辺(面)の長さが同じです。 通常の六角形でのみ動作します。 通常、六角形のグリッドは、水平方向(鋭い上部)と垂直方向(平坦な上部)を使用します。
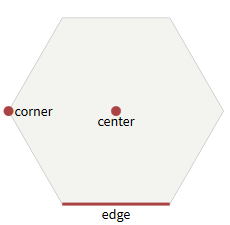
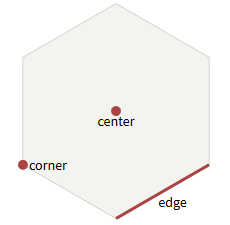 平らな(左)と鋭い(右)上部の六角形
平らな(左)と鋭い(右)上部の六角形六角形には6つの面があります。 各面は2つの六角形に共通です。 六角形には6つのコーナーポイントがあります。 各コーナーポイントは3つの六角形に共通です。
メッシュの一部 (正方形、六角形、三角形)
についての私の記事で 、中心点、面、コーナーポイントについて詳しく読むことができます。
角度
通常の六角形では、内角は120°です。 6つの「くさび」があり、それぞれが60°の内角を持つ正三角形です。 コーナーポイント
iは、
(60° * i) + 30°距離で、中心の
centerから
size単位です。 コード内:
function hex_corner(center, size, i): var angle_deg = 60 * i + 30 var angle_rad = PI / 180 * angle_deg return Point(center.x + size * cos(angle_rad), center.y + size * sin(angle_rad))
六角形を塗りつぶすには、
hex_corner(…, 0)から
hex_corner(…, 5)多角形の頂点を取得する必要があります。 六角形のアウトラインを描画するには、これらの頂点を使用してから、
hex_corner(…, 0)再度線を描画する必要があります。
2つの方向の違いは、xとyが場所を変えることで、角度が変化することです:平らな上部の六角形の角度は0°、60°、120°、180°、240°、300°、および鋭い上部-30 °、90°、150°、210°、270°、330°。
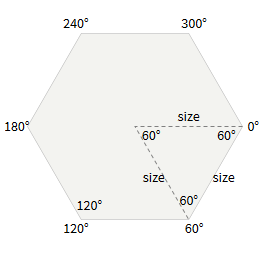
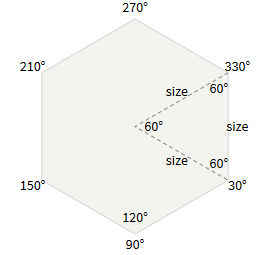 平らで尖った六角形の角度
平らで尖った六角形の角度サイズと場所
ここで、いくつかの六角形を一緒に配置したいと思います。 水平方向では、六角形の
height = size * 2は
height = size * 2です。 隣接する六角形間の垂直距離
vert = height * 3/4 。
六角形の
width = sqrt(3)/2 * height 。 隣接する六角形間の水平距離
horiz = width 。
一部の六角形ゲームは、通常の六角形と正確に一致しないピクセルアートを使用します。 このセクションで説明する角度と位置の式は、このような六角形の寸法と一致しません。 六角形のメッシュアルゴリズムについて説明している残りの記事は、六角形がわずかに伸縮している場合でも適用できます。
座標系
六角形をグリッドに組み立て始めましょう。 正方形グリッドの場合、構築する明らかな方法は1つだけです。 六角形には、多くのアプローチがあります。 一次表現として立方座標を使用することをお勧めします。 軸座標またはオフセット座標を使用して、マップを保存し、ユーザーに座標を表示する必要があります。
オフセット座標
最も一般的なアプローチは、後続の各列または行をオフセットすることです。 列は
colまたは
q示されます。 行は
rowまたは
r示されます。 奇数または偶数の列/行をオフセットできるため、水平および垂直の六角形には2つのオプションがあります。
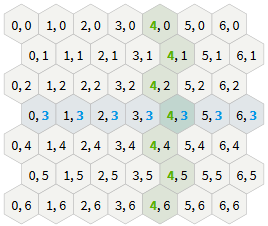 水平配置「odd-r」
水平配置「odd-r」 水平配置「偶数-r」
水平配置「偶数-r」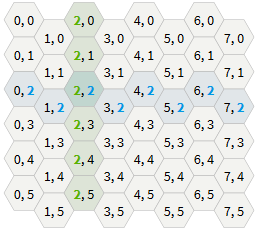 縦配置「odd-q」
縦配置「odd-q」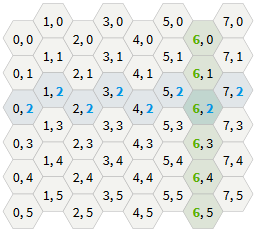 縦配置「偶数-q」
縦配置「偶数-q」立方座標
六角形のグリッドを見るもう1つの方法は、正方形のグリッドのように
2つではなく
3つの主軸を見ることです。 それらはエレガントな対称性を示しています。
立方体のグリッドを取り、
x + y + z = 0で対角平面を
切り取り x + y + z = 0 。 これは奇妙な考えですが、六角形グリッドのアルゴリズムを簡素化するのに役立ちます。 特に、デカルト座標の標準操作を使用できます。座標の加算と減算、スカラー値による乗算と除算、および距離。
立方体のグリッド上の3つの主軸と、六角形のグリッドの6つの
対角線方向との関係に注目してください。 グリッドの対角軸は、六角形のグリッドの主方向に対応しています。
六角形キューバ正方形と立方体のグリッドのアルゴリズムはすでにあるため、立方座標を使用すると、これらのアルゴリズムを六角形のグリッドに適合させることができます。 ほとんどの記事のアルゴリズムにこのシステムを使用します。 異なる座標系のアルゴリズムを使用するには、3次座標を変換し、アルゴリズムを実行してから元に戻します。
六角形のグリッドに対して立方座標がどのように機能するかを学びます。 六角形を選択すると、3つの軸に対応する立方体座標が選択されます。
- 立方体のグリッドの各方向は、六角形のグリッド上の線に対応しています。
zが0、1、2、3に等しい六角形を選択して、接続を確認してください。 線は青でマークされています。 x (緑)とy (ライラック)についても同じことを試してください。
- 六角形グリッドの各方向は、立方体のグリッドの2つの方向の組み合わせです。 たとえば、六角形グリッドの「北」は
+yと-z間にあるため、「北」への各ステップはyを1増加させ、 zを1減少させます。
立方体座標は、六角形のグリッド座標系の賢い選択です。 条件は
x + y + z = 0ため、アルゴリズムで保存する必要があります。 また、この条件により、各六角形に常に標準座標が存在することが保証されます。
立方体と六角形には多くの異なる座標系があります。 それらのいくつかでは、条件は
x + y + z = 0とは異なり
x + y + z = 0 。 多くのシステムの1つだけを示しました。 また、
xy 、
yz 、
zxを使用して3次座標を作成することもできますが、これらには独自の興味深いプロパティのセットがありますが、ここでは考慮しません。
ただし、この形式で地図を保存する方法がわからないため、座標に3つの数字を保存したくないと考えることができます。
軸座標
「台形」とも呼ばれる軸座標系は、3次座標系の2つまたは3つの座標に基づいて構築されます。 条件
x + y + z = 0ため、3番目の座標は必要ありません。 軸座標は、マップを保存し、ユーザーに座標を表示するのに役立ちます。 3次座標の場合と同様に、デカルト座標での加算、減算、乗算、除算の標準操作を使用できます。
多くの立方座標系と多くの軸があります。 このガイドでは、すべての組み合わせを扱いません。 2つの変数、
q (列)と
r (行)を選択します。 この記事のスキームでは、
qは
xに対応し、
rは
zに対応しますが、さまざまな対応を取得して回路を回転および回転させることができるため、このような対応は任意です。
変位グリッドを超えるこのシステムの利点は、アルゴリズムの理解度が高いことです。 このシステムの欠点は、長方形のカードを保管するのが少しおかしいことです。 マップの保存に関するセクションを参照してください。 一部のアルゴリズムは3次座標ではさらに明確ですが、条件
x + y + z = 0があるため、3番目の暗黙の座標を計算し、これらのアルゴリズムで使用できます。 私のプロジェクトでは、
q 、
r 、
s軸を呼び出すため、条件は
q + r + s = 0になり、必要に応じて
s = -q - r計算できます。
軸
変位座標は、正方形グリッドに使用される標準のデカルト座標と一致するため、ほとんどの人が最初に考えるものです。 残念ながら、2つの軸のうちの1つが「コートに逆らう」必要があり、結果としてすべてが複雑になります。 キュービックおよびアキシャルシステムは「ウールに沿って」移動し、アルゴリズムは単純ですが、カードの保管はもう少し複雑です。 「交互」または「二重」と呼ばれる別のシステムがありますが、ここではそれを考慮しません。 キュービックやアキシャルよりも作業しやすい人もいます。
変位座標、立方および軸軸は、対応する座標が増加する方向です。 軸に垂直なのは、座標が一定のままである線です。 上記のグリッド図は、垂線を示しています。
座標変換
プロジェクトで軸座標または変位座標を使用する可能性がありますが、多くのアルゴリズムは立方座標でより簡単に表現できます。 したがって、システム間で座標を変換できる必要があります。
軸座標は立方体と密接に関連しているため、変換は簡単です。
# q = x r = z # x = q z = r y = -xz
コードでは、これらの2つの関数は次のように記述できます。
function cube_to_hex(h): # var q = hx var r = hz return Hex(q, r) function hex_to_cube(h): # var x = hq var z = hr var y = -xz return Cube(x, y, z)
オフセット座標はかなり複雑です:
# -q col = x row = z + (x + (x&1)) / 2 # -q x = col z = row - (col + (col&1)) / 2 y = -xz # -q col = x row = z + (x - (x&1)) / 2 # -q x = col z = row - (col - (col&1)) / 2 y = -xz # -r col = x + (z + (z&1)) / 2 row = z # -r x = col - (row + (row&1)) / 2 z = row y = -xz # -r col = x + (z - (z&1)) / 2 row = z # -r x = col - (row - (row&1)) / 2 z = row y = -xz
実装上の注意:数値が偶数(0)か奇数(1)かを判断するために、a%2(
剰余による除算 )の代わりに&1(
ビット単位の「AND」 )を使用します。 詳細な説明について
は、実装のメモページを参照
してください 。
隣接する六角形
1つの六角形が指定されていますが、次の6つの六角形はどれですか? ご想像のとおり、答える最も簡単な方法は、3次座標で、軸座標でかなり単純で、変位座標で少し難しいです。 6つの「対角」六角形を計算する必要がある場合もあります。
立方座標
六角形の座標で1つのスペースを移動すると、3つの立方体座標の1つが+1変化し、もう1つが-1変化します(合計は0のままでなければなりません)。 3つの可能な座標は+1変化し、残りの2つの座標は-1変化します。 これにより、6つの変更が可能になります。 それぞれが六角形の方向の1つに対応します。 最も簡単で最速の方法は、コンパイル時に変更を事前に計算し、
Cube(dx, dy, dz) 3次座標テーブル
Cube(dx, dy, dz)に配置することです。
var directions = [ Cube(+1, -1, 0), Cube(+1, 0, -1), Cube( 0, +1, -1), Cube(-1, +1, 0), Cube(-1, 0, +1), Cube( 0, -1, +1) ] function cube_direction(direction): return directions[direction] function cube_neighbor(hex, direction): return cube_add(hex, cube_direction(direction))
軸座標
前と同様に、最初にキュービックシステムを使用します。
Cube(dx, dy, dz)テーブル
Cube(dx, dy, dz)を
Cube(dx, dy, dz)し、
Hex(dq, dr)テーブル
Hex(dq, dr)変換します。
var directions = [ Hex(+1, 0), Hex(+1, -1), Hex( 0, -1), Hex(-1, 0), Hex(-1, +1), Hex( 0, +1) ] function hex_direction(direction): return directions[direction] function hex_neighbor(hex, direction): var dir = hex_direction(direction) return Hex(hex.q + dir.q, hex.r + dir.r)
オフセット座標
軸座標では、グリッドのどこにいるかに応じて変更を加えます。 列/行のオフセットにいる場合、ルールはオフセットのない列/行の場合とは異なります。
前と同様に、
colおよび
row追加する数値のテーブルを作成します。 ただし、今回は2つの配列があります。1つは奇数列/行用で、もう1つは偶数列/行用です。 上記のグリッドマップで
(1,1)見て、6つの各方向に移動するときに
colと
rowどのように変化するかを確認してください。 ここで
(2,2)プロセスを繰り返します。 テーブルとコードは、4種類のオフセットグリッドごとに異なります。それぞれの種類のグリッドに対応するコードを示します。
奇数 var directions = [ [ Hex(+1, 0), Hex( 0, -1), Hex(-1, -1), Hex(-1, 0), Hex(-1, +1), Hex( 0, +1) ], [ Hex(+1, 0), Hex(+1, -1), Hex( 0, -1), Hex(-1, 0), Hex( 0, +1), Hex(+1, +1) ] ] function offset_neighbor(hex, direction): var parity = hex.row & 1 var dir = directions[parity][direction] return Hex(hex.col + dir.col, hex.row + dir.row)
 偶数(EVEN)および奇数(ODD)行のグリッドでもr
偶数(EVEN)および奇数(ODD)行のグリッドでもr var directions = [ [ Hex(+1, 0), Hex(+1, -1), Hex( 0, -1), Hex(-1, 0), Hex( 0, +1), Hex(+1, +1) ], [ Hex(+1, 0), Hex( 0, -1), Hex(-1, -1), Hex(-1, 0), Hex(-1, +1), Hex( 0, +1) ] ] function offset_neighbor(hex, direction): var parity = hex.row & 1 var dir = directions[parity][direction] return Hex(hex.col + dir.col, hex.row + dir.row)
 偶数(EVEN)および奇数(ODD)行のグリッド奇数
偶数(EVEN)および奇数(ODD)行のグリッド奇数 var directions = [ [ Hex(+1, 0), Hex(+1, -1), Hex( 0, -1), Hex(-1, -1), Hex(-1, 0), Hex( 0, +1) ], [ Hex(+1, +1), Hex(+1, 0), Hex( 0, -1), Hex(-1, 0), Hex(-1, +1), Hex( 0, +1) ] ] function offset_neighbor(hex, direction): var parity = hex.col & 1 var dir = directions[parity][direction] return Hex(hex.col + dir.col, hex.row + dir.row)
 偶数(EVEN)および奇数(ODD)列のグリッドでもq
偶数(EVEN)および奇数(ODD)列のグリッドでもq var directions = [ [ Hex(+1, +1), Hex(+1, 0), Hex( 0, -1), Hex(-1, 0), Hex(-1, +1), Hex( 0, +1) ], [ Hex(+1, 0), Hex(+1, -1), Hex( 0, -1), Hex(-1, -1), Hex(-1, 0), Hex( 0, +1) ] ] function offset_neighbor(hex, direction): var parity = hex.col & 1 var dir = directions[parity][direction] return Hex(hex.col + dir.col, hex.row + dir.row)
 偶数(EVEN)および奇数(ODD)列のグリッド
偶数(EVEN)および奇数(ODD)列のグリッド上記のルックアップテーブルを使用することが、ネイバーを計算する最も簡単な方法です。 興味がある場合は、
これらの数値の抽出についても読むことができ
ます 。
対角線
六角形の座標の「対角」空間を移動すると、3つの立方体座標の1つが±2変化し、他の2つが∓1変化します(合計は0のままでなければなりません)。
var diagonals = [ Cube(+2, -1, -1), Cube(+1, +1, -2), Cube(-1, +2, -1), Cube(-2, +1, +1), Cube(-1, -1, +2), Cube(+1, -2, +1) ] function cube_diagonal_neighbor(hex, direction): return cube_add(hex, diagonals[direction])
前と同様に、結果を計算した後、3つの座標のいずれかを折り畳むことにより、これらの座標を軸に変換するか、オフセット座標に変換できます。
距離
立方座標
立方体座標系では、各六角形は3次元空間の立方体です。 隣接する六角形は、互いに1の距離にある六角形のグリッドにありますが、立方体のグリッドには2の距離にあります。 これにより、距離の計算が簡単になります。 正方形のグリッドでは、
マンハッタン距離は
abs(dx) + abs(dy)です。 立方体のグリッドでは、マンハッタン距離は
abs(dx) + abs(dy) + abs(dz)です。 六角形のグリッドの距離は、その半分に等しくなります。
function cube_distance(a, b): return (abs(ax - bx) + abs(ay - by) + abs(az - bz)) / 2
このエントリに相当するのは、3つの座標の1つが他の2つの座標の合計でなければならず、それを距離として取得するという式です。 以下の半分の形式または最大値の形式を選択できますが、同じ結果が得られます。
function cube_distance(a, b): return max(abs(ax - bx), abs(ay - by), abs(az - bz))
図では、最大値が色で強調表示されています。 また、各色は6つの「対角線」方向の1つを表していることに注意してください。
軸座標
アキシャルシステムでは、3番目の座標は暗黙的に表現されます。 距離を計算するためにアキシャルからキュービックシステムに
変換しましょう:
function hex_distance(a, b): var ac = hex_to_cube(a) var bc = hex_to_cube(b) return cube_distance(ac, bc)
あなたのケースのコンパイラが
hex_to_cubeと
cube_distance (インラインで)埋め込む場合、次のコードを生成します:
function hex_distance(a, b): return (abs(aq - bq) + abs(aq + ar - bq - br) + abs(ar - br)) / 2
軸座標の六角形間の距離を記録する多くの異なる方法がありますが、記録方法に関係なく
、軸システムの六角形間の距離は立方システムのマンハッタン距離から抽出されます 。 たとえば、
ここで説明
する 「差分の差」は、
aq + ar - bq - brという表記から
aq - bq + ar - brとして取得され、
cube_distance二分
cube_distanceではなく最大値形式を使用します。 3次座標との関係を見ると、それらはすべて類似しています。
オフセット座標
軸座標と同様に、変位の座標を3次座標に変換し、3次システムの距離を使用します。
function offset_distance(a, b): var ac = offset_to_cube(a) var bc = offset_to_cube(b) return cube_distance(ac, bc)
多くのアルゴリズムで同じテンプレートを使用します。六角形から立方体への変換、アルゴリズムの立方体バージョンの実行、立方体の結果の六角形の座標(軸座標またはオフセット座標)への変換。
線画
ある六角形から別の六角形に線を引く方法は?
線形補間を使用して
線を描画します 。 ラインは
N+1ポイントで均等にサンプリングされ、これらのサンプルがどの六角形であるかが計算されます。
- 最初に、端点間の六角形の距離である
Nを計算します。 - 次に、ポイントAとBの間で
N+1ポイントを均等にサンプリングします。線形補間を使用して、 0からNまでの値iそれらを含む)について、各ポイントがA + (B - A) * 1.0/N * iます。 図では、これらの制御点は青で示されています。 結果は浮動小数点座標です。 - 各制御点(浮動)を六角形(int)に変換します。 このアルゴリズムは
cube_roundと呼ばれcube_round (以下を参照)。
すべてをまとめてAからBに線を引きます。
function lerp(a, b, t):
注:
cube_lerpが2つの六角形の間の境界上の点を返す場合があります。 次に、 cube_roundそれをある方向または別の方向にシフトします。 線を同じ方向に動かすと、線がよりきれいに見えます。 これは、サイクルを開始する前に、イプシロン六角形Cube(1e-6, 1e-6, -2e-6)を一方または両方のエンドポイントに追加することで実行できます。 これにより、線が一方向に「押し出され」、面の境界に落ちないようになります。- 正方形グリッドのDDAラインアルゴリズムは、
Nを各軸に沿った最大距離に相当します。 六角形のグリッドでの距離に似ている立方体空間でも同じことを行います。 cube_lerp関数は、floatの座標を持つキューブを返す必要があります。 静的型付けを使用する言語でプログラミングする場合、 Cube型は使用できません。 代わりに、 FloatCubeのタイプを定義するか、別のタイプを定義したくない場合は、ラインレンダリングコードに関数を埋め込む(インライン)ことができます。- (インライン)
cube_lerpを埋め込み、ループ外でBx-Ax 、 Bx-Ayおよび1.0/N計算することにより、コードを最適化できます。 乗算は、繰り返しの合計に変換できます。 結果は、DDAラインアルゴリズムのようなものです。 - 線を描画するには、軸座標または3次座標を使用しますが、オフセット座標を使用する場合は、 この記事を参照してください 。
- 線を描くための多くのオプションがあります。 「オーバーコーティング」が必要になる場合があります。 六角形のスーパーコーティングされた線を描くためのコードが送られましたが、まだ勉強していません。
可動範囲
座標範囲
特定の六角形の中心と範囲
Nどの六角形がその
Nステップ以内にありますか?
六角形間の距離の式の逆の作業を行うことができます
distance = max(abs(dx), abs(dy), abs(dz)) 。
N内のすべての六角形を見つけるには、
max(abs(dx), abs(dy), abs(dz)) ≤ N これは、
abs(dx) ≤ Nおよび
abs(dy) ≤ Nおよび
abs(dz) ≤ N 3つの値がすべて必要であることを意味します
abs(dz) ≤ N 絶対値を削除すると、
-N ≤ dy ≤ Nおよび
-N ≤ dy ≤ Nおよび
-N ≤ dy ≤ N得られます
-N ≤ dz ≤ N コードでは、これはネストされたループになります。
var results = [] for each -N ≤ dx ≤ N: for each -N ≤ dy ≤ N: for each -N ≤ dz ≤ N: if dx + dy + dz = 0: results.append(cube_add(center, Cube(dx, dy, dz)))
このループは機能しますが、非常に非効率的です。 ループで反復処理するすべての
dz値のうち、実際にキューブ条件
dx + dy + dz = 0満たすのは1つだけです。
代わりに、dz条件を満足する値を直接計算します。 var results = [] for each -N ≤ dx ≤ N: for each max(-N, -dx-N) ≤ dy ≤ min(N, -dx+N): var dz = -dx-dy results.append(cube_add(center, Cube(dx, dy, dz)))
このサイクルは、必要な座標にのみ沿っています。図では、各範囲は行のペアです。各行は不等式です。6つの不等式を満たすすべての六角形を取ります。交差する範囲
複数の範囲にある六角形を見つける必要がある場合は、六角形のリストを生成する前に範囲を横断できます。代数または幾何学の観点からこの問題にアプローチできます。代数的には、各領域はの形式で不等式の条件として表され-N ≤ dx ≤ N、これらの条件の共通部分を見つける必要があります。幾何学的には、各領域は3次元空間の立方体であり、3次元空間で2つの立方体を交差させて、3次元空間で直方体を取得します。次に、平面x + y + z = 0に投影して六角形を取得します。この問題を代数的に解決します。第一に、我々は条件を書き換え-N ≤ dx ≤ N、より一般的な形で、かつ取ると。同じことをしましょうx min ≤ x ≤ x maxx min = center.x - Nx max = center.x + Nyそしてz、その結果、前のセクションからコードの一般的なビューを取得します: var results = [] for each xmin ≤ x ≤ xmax: for each max(ymin, -x-zmax) ≤ y ≤ min(ymax, -x-zmin): var z = -xy results.append(Cube(x, y, z))
2の交点が範囲a ≤ x ≤ bとc ≤ x ≤ dされますmax(a, c) ≤ x ≤ min(b, d)。六角形の領域はの範囲として表現するのでx、y、z我々は、個々のバンドのそれぞれを横断することができx、y、z、その後交差点における六角形のリストを生成するために、ネストされたループを使用します。一方の領域のために我々は六角形を取ると、に類似すると。六角形の二つの領域の交点に、我々は受け入れると最大=分(H1.x + N、 H2.x + N)は、 同様であると。同じパターンは、3つ以上の領域を交差させるために機能します。x min = Hx - Nx max = Hx + Nyzx min = max(H1.x - N, H2.x - N)xyz障害物
障害物がある場合は、距離制限を埋めるのが最も簡単です(ワイド検索)。次の図では、4つの動きに制限されています。コードではfringes[k]、これはkステップで達成できるすべての六角形の配列です。メインサイクルを通過するたびに、レベルk-1をlevelに拡張しますk。 function cube_reachable(start, movement): var visited = set() add start to visited var fringes = [] fringes.append([start]) for each 1 < k ≤ movement: fringes.append([]) for each cube in fringes[k-1]: for each 0 ≤ dir < 6: var neighbor = cube_neighbor(cube, dir) if neighbor not in visited, not blocked: add neighbor to visited fringes[k].append(neighbor) return visited
ターン
特定の六角形ベクトル(2つの六角形の差)に対して、別の六角形を指すように回転する必要がある場合があります。これは、1/6サークルターンに固執する場合、3次座標で簡単に実行できます。右に60°回転すると、各座標が右に1ポジション移動します。 [ x, y, z] to [-z, -x, -y]
左に60°回転すると、各座標が左に1ポジション移動します。 [ x, y, z] to [-y, -z, -x]
[元の記事で]スキームを「再生」すると、60°回転するごとに符号が変化し、座標が物理的に「回転」することがわかります。120°回転すると、記号は再び同じになります。180度回転すると符号が変わりますが、座標は元の位置に回転します。位置Pが中心位置Cを中心に回転し、新しい位置Rに至る完全なシーケンスを次に示します。- PおよびCの位置を3次座標に変換します。
- :減算することにより、センターベクトル算出
P_from_C = P - C = Cube(Px - Cx, Py - Cy, Pz - Cz)。 P_from_C上記のようにベクトルを回転し、最終的なベクトルに指定を割り当てR_from_Cます。- 形質転換ベクターは、追加の中心位置に戻ります:
R = R_from_C + C = Cube(R_from_C.x + Cx, R_from_C.y + Cy, R_from_C.z + Cz)。 - Rの3次位置を目的の座標系に変換します。
変換にはいくつかの段階がありますが、それぞれが非常に単純です。軸座標で直接回転を定義することでこれらのステップの一部を短縮できますが、六角形ベクトルはオフセット座標では機能せず、オフセット座標のステップを短縮する方法がわかりません。stackexchangeでローテーションを計算する他の方法の説明も参照してください。指輪
シンプルなリング
特定の六角形が特定の半径のリングに属しているかどうかを調べるには、radiusこの六角形から中心までの距離を計算し、等しいかどうかを調べる必要がありますradius。このようなすべての六角形のリストを取得するにradiusは、中心からステップを踏み、リングに沿ったパスに沿って回転したベクトルに従う必要があります。 function cube_ring(center, radius): var results = [] # radius == 0; , ? var cube = cube_add(center, cube_scale(cube_direction(4), radius)) for each 0 ≤ i < 6: for each 0 ≤ j < radius: results.append(cube) cube = cube_neighbor(cube, i) return results
このコードcubeは、図の中心から角に向かう大きな矢印で示されるリングから始まります。まず、角度4を選択しました。これは、方向番号が移動するパスに対応しているためです。別の開始角度が必要な場合があります。内側のサイクルの各段階でcube、リングに沿って1つの六角形を移動します。スルー6 * radius始めた場所の手順は完了します。スパイラルリング
らせんパターンに沿ってリングに沿って通過すると、リングの内側の部分を埋めることができます。 function cube_spiral(center, radius): var results = [center] for each 1 ≤ k ≤ radius: results = results + cube_ring(center, k) return results
大きな六角形の面積は、すべての円の合計に中心の1を加えたものです。面積を計算するには、次の式を使用します。この方法で六角形をバイパスすることは、移動範囲の計算にも使用できます(上記を参照)。範囲
与えられた距離で与えられた位置から見えるものは何で、障害物によってブロックされていませんか?これを判断する最も簡単な方法は、特定の範囲内の各六角形に線を引くことです。線が壁に合わない場合は、六角形が表示されます。[元の記事の図]の六角形に沿ってマウスを移動すると、これらの六角形への線の描画と、線が交わる壁が表示されます。このアルゴリズムは広い範囲で低速になる可能性がありますが、実装は簡単なので、最初から始めることをお勧めします。可視性にはさまざまな定義があります。イニシャルの中心から別の六角形の中心を見たいですか?スタートの中心から別の六角形の一部を見たいですか?たぶん、開始点のどこからでも別の六角形の一部ですか?完全な六角形よりも少ないビューへの障害?スコープは、一見思われるよりもunningで多様な概念です。最も単純なアルゴリズムから始めましょう。ただし、プロジェクトの答えが正しく計算されることを期待してください。単純なアルゴリズムで非論理的な結果が得られる場合もあります。でクラークVerbruggeマニュアル範囲を計算するためのアルゴリズムを説明し、「中央から開始して外側に移動します。」GithubにあるDueloプロジェクトも参照してください。道順を含む範囲のオンラインデモ。また、2D可視性の計算に関する私の記事を読むことができます。これには、六角形を含む多角形で動作するアルゴリズムがあります。ローグライクファンコミュニティには、正方形グリッド用の優れたアルゴリズムセットがあります(こちら、こちら、こちらをご覧ください)。それらのいくつかは、六角形のグリッドに適応させることができます。六角形からピクセル
六角形からピクセルに変換するには、「ジオメトリ」セクションに示されているサイズと場所のスキームを調べると便利です。軸座標の場合、六角形からピクセルへの変換は、基底ベクトルを考慮してアプローチする必要があります。図では、矢印A→Qは基底ベクトルqであり、A→Rは基底ベクトルrです。ピクセル座標はq_basis * q + r_basis * rです。たとえば、(1、1)のBは基底ベクトルqとrの合計です。行列ライブラリを使用すると、操作は単純な行列乗算です。ただし、ここではマトリックスなしでコードを記述します。軸グリッドのためx = q、z = r次のように私は、このガイドで使用することは、変換は次のようになります平らな上面を有する六角形のため function hex_to_pixel(hex): x = size * 3/2 * hex.q y = size * sqrt(3) * (hex.r + hex.q/2) return Point(x, y)
先のとがったトップ用 function hex_to_pixel(hex): x = size * sqrt(3) * (hex.q + hex.r/2) y = size * 3/2 * hex.r return Point(x, y)
マトリックスアプローチは、後でピクセルの座標を六角形の座標に変換する必要があるときに便利です。マトリックスを逆にするだけです。3次座標の場合、3次基底ベクトル(x、y、z)を使用するか、最初にそれらを軸に変換してから軸基底ベクトル(q、r)を使用できます。オフセット座標の場合、列番号または行番号をシフトする必要があります(整数ではなくなります)。その後、x軸とy軸に関連付けられたベースベクトルqとrを使用できます:Odd-r function offset_to_pixel(hex): x = size * sqrt(3) * (hex.col + 0.5 * (hex.row&1)) y = size * 3/2 * hex.row return Point(x, y)
でもr function offset_to_pixel(hex): x = size * sqrt(3) * (hex.col - 0.5 * (hex.row&1)) y = size * 3/2 * hex.row return Point(x, y)
奇数 function offset_to_pixel(hex): x = size * 3/2 * hex.col y = size * sqrt(3) * (hex.row + 0.5 * (hex.col&1)) return Point(x, y)
でもq function offset_to_pixel(hex): x = size * 3/2 * hex.col y = size * sqrt(3) * (hex.row - 0.5 * (hex.col&1)) return Point(x, y)
残念ながら、変位座標には、マトリックスで使用できる基底ベクトルがありません。これが、オフセット座標でピクセルから六角形への変換がより難しい理由の1つです。別のアプローチ:オフセット座標を3次/軸座標に変換してから、3次/軸座標のピクセルへの変換を使用します。最適化中に変換コードを埋め込むことにより、上記と同じ結果になります。ピクセルから六角形へ
最も一般的な質問の1つは、ピクセルの位置(たとえば、マウスクリック)を取得し、六角形のグリッド座標に変換する方法ですか?これが軸座標または3次座標でどのように行われるかを示します。オフセット座標の場合、最も簡単な方法は、3次座標を最後にオフセット座標に変換することです。- まず、六角形からピクセルへの変換を逆にします。これにより、図に小さな青い円で示されている六角形の小数座標が得られます。
- 次に、六角形の小数座標を含む六角形を定義します。図では、六角形が強調表示されています。
我々が掛けた六角形のピクセル座標に座標変換するためにq、r基底ベクトルが得られx、y。これは行列乗算と見なすことができます。尖ったトップのマトリックスは次のとおりです。ピクセルの座標を六角形の座標に戻すことは、かなり簡単です。行列を反転できます:これらの計算により、qおよびの分数軸座標(浮動)が得られrます。この関数hex_round()は、分数軸座標を六角形の整数軸座標に変換します。軸方向の尖ったトップのコードは次のとおりです。 function pixel_to_hex(x, y): q = (x * sqrt(3)/3 - y / 3) / size r = y * 2/3 / size return hex_round(Hex(q, r))
そして、ここに軸方向のフラットトップ六角形のコードがあります: function pixel_to_hex(x, y): q = x * 2/3 / size r = (-x / 3 + sqrt(3)/3 * y) / size return hex_round(Hex(q, r))
これらの3行のコードは、ピクセルの位置を六角形の軸座標に変換します。オフセット座標を使用する場合は、を使用しますreturn cube_to_hex(cube_round(Cube(q, -qr, r)))。ピクセルを六角形に変換する方法は他にもたくさんあります。で、このページは私にはよく知られています。最も近い六角形に丸めます。
浮動小数点を使用して3次座標(x、y、z)を取得する場合があり、どの六角形にあるかを調べる必要があります。これは、線を描画し、ピクセルから六角形に変換することで明確になります。浮動小数点値を整数値に変換することは丸めと呼ばれるため、このアルゴリズムを呼び出しましたcube_round。3次浮動小数点座標でx + y + z = 0も、3次座標で。したがって、各コンポーネントを最も近い整数に丸めましょう(rx, ry, rz)。ただし、x + y + z = 0丸めた後、という保証はありませんrx + ry + rz = 0。したがって、条件がrx + ry + rz = 0真になるように、最大の変更でコンポーネントを変更します。たとえば、変化がy abs(ry-y)大きい場合abs(rx-x)そして、abs(rz-z)それをに変更しry = -rx-rzます。これは私たちにそれを保証しrx + ry + rz = 0ます。アルゴリズムは次のとおりです。 function cube_round(h): var rx = round(hx) var ry = round(hy) var rz = round(hz) var x_diff = abs(rx - hx) var y_diff = abs(ry - hy) var z_diff = abs(rz - hz) if x_diff > y_diff and x_diff > z_diff: rx = -ry-rz else if y_diff > z_diff: ry = -rx-rz else: rz = -rx-ry return Cube(rx, ry, rz)
非キュービック座標の場合、キュービック座標に変換し、丸めアルゴリズムを使用してから元に戻すのが最も簡単です。 function hex_round(h): return cube_to_hex(cube_round(hex_to_cube(h)))
実装に関する注意:cube_roundおよびhex_roundintではなくfloatで座標を取得します。Cubeとclassesを作成した場合Hex、整数の代わりに浮動小数点数を渡すことができる動的型付けの言語、および統一型の型を持つ静的型付けの言語で正常に動作します。ただし、静的型付けを使用するほとんどの言語では、float座標用に別のクラス/構造体型が必要でありcube_round、typeがありFloatCube → Cubeます。必要な場合はhex_round、代わりにFloatHex → Hexヘルパー関数をfloatcube_to_floathex使用しcube_to_hexます。パラメーター化された型(C ++、Haskellなど)を持つ言語では、TがintまたはfloatであるCubeを定義できます。または書くことができますcube_round この関数のみに新しい型を定義する代わりに、入力として3つの浮動小数点数を取得します。地図を軸座標で保存する
ほとんどの場合、軸座標系は、長方形のマップを使用するときにスペースを無駄に消費するため、苦情を引き起こします。これが変位座標系の理由の1つです。ただし、三角形または六角形のマップを使用すると、六角形のすべての座標系でスペースが消費されます。 1つの戦略を使用して、これらすべてのタイプのカードを保存できます。 長方形の地図
長方形の地図 三角形の地図
三角形の地図 六角形の地図
六角形の地図 菱形の地図図では、未使用のスペースは各線の左右にあることに注意してください(菱形の地図を除く)。これにより、カードストレージ戦略の3つのオプションが提供されます。
菱形の地図図では、未使用のスペースは各線の左右にあることに注意してください(菱形の地図を除く)。これにより、カードストレージ戦略の3つのオプションが提供されます。- . . . , .
- - . , .
q,r hash_table(hash(q,r)) . / , . - . . . . , 0, .
, « ». q,r , array[r][q - first_column[r]] . / , . first_column .
, « » « », .
first_column[r] == -floor(r/2) . array[r][q + r/2] , .- , ,
first_column[r] == 0 , access array[r][q] — ! , - ( ), array[r][q+r] . N , N = max(abs(x), abs(y), abs(z) , first_column[r] == -N - min(0, r) . array[r][q + N + min(0, r)] . - r < 0 , array[r + N][q + N + min(0, r)] .- ,
array[r][q] .
一部のゲームでは、カードの端を「くっつける」必要があります。正方形マップは、x軸(球体にほぼ対応)またはx軸とy軸(トーラスにほぼ対応)に沿ってのみラップできます。最小化は、要素の形状ではなく、マップの形状に依存します。正方形座標マップの最小化は、オフセット座標で簡単に実行できます。六角形のマップを3次座標で折り畳む方法を示します。マップの中心に関しては、6つの「ミラー」センターがあります。マップを離れるとき、メインマップに再び戻るまで、最も近いミラー中心を引きます。 [元の記事]の図で、中央の地図から離れて、鏡の中心の1つが反対側から地図に入る様子を観察します。最も簡単な実装は、回答を事前に計算することです。マップから出る各六角形、反対側の対応するキューブを格納するルックアップテーブルを作成します。6つのミラーセンターのMそれぞれと、マップ上の各位置について、L保存しmirror_table[cube_add(M, L)] = Lます。ミラーのテーブルにある六角形を計算するたびに、ミラーリングされていないバージョンに置き換えます。半径のある六角形のマップでは、Nミラーの中心Cube(2*N+1, -N, -N-1)も6ターンになります。道を探す
A *検索アルゴリズム、DijkstraまたはFloyd-Warshallアルゴリズムなど、グラフでパス検索を使用する場合、六角形グリッドでのパス検索は、正方形グリッドでのパス検索と変わりません。パス検索ガイドの説明とコードは、六角形のグリッドに適用されます。[元の記事では、この例はインタラクティブで、マウスクリックで壁を追加および削除できます]- 隣人。パス検索ガイドに示されているコード例は、要素に隣接する位置を取得するために呼び出しています
graph.neighbors。これには、「近くの六角形」セクションの機能を使用します。貫通できない隣接する六角形を除去します。 - ヒューリスティック。アルゴリズムA *のコード例では
heuristic、2つの位置間の距離を取得する関数が使用されています。距離の式に移動コストを掛けて使用します。たとえば、移動に六角形あたり5ユニットのコストがかかる場合、距離に5を掛けます。
追加の読書
C ++、Java、C#、Javascript、Haxe、Pythonのコード例を使用して、六角形グリッドの独自のライブラリを実装するためのガイドがあります。- グリッドガイドでは、軸座標系と、正方形、三角形、六角形の面と角度の処理について説明します。また、正方形と六角形のグリッドの接続方法についても説明します。
- , , , 1996 .
- 1994 rec.games.programmer .
- DevMag , , , . PDF , . ! GameLogic Grids Unity.
- .
- : ( ), , () ().
- Rot.js : (), ( ), (), .
- : ?
- .
- .
- .
- , .
- HexPart , .
- ?
- , . [ ]
- Hexnet , , , .
- PDF , .
- ; .
- Hex-Grid Utilities — C# , , , . MIT.
- Reddit , Hacker News MetaFilter .
この記事の[元の]コードは、HaxeとJavascriptの混合で記述されています:Cube.hx、Hex.hx、Grid.hx、ScreenCoordinate.hx、ui.jsおよびcubegrid.js(キューブ/六角形のアニメーション用)。ただし、六角形グリッドの独自のライブラリを作成する場合は、代わりに実装ガイドを検討することをお勧めします。このガイドをさらに拡張したいと思います。Trelloにリストがあります。