ビットコインの概要-暗号化

ビットコインが引き続き注目を集めている理由の1つは、その例外的な「数学」です。 中本Sは、参加者間の信頼がまったくなくても機能するシステムを作成することができました。 すべての相互作用は厳密な数学に基づいており、人的要因はありません。多くの人が考えるように、それはピアツーピアネットワークではなく、革命のアイデアでした。 したがって、私はビットコインの数学的基礎に最初の章を捧げることにしました。

以下では、楕円曲線、ECC、秘密/公開キーなど、最も基本的なことを説明しようとします。 可能であれば、主にPython 2.7で、もし何か明確でない場合は、コメントで質問してください。

本

• ビットコインの概要-暗号化
• ビットコインの概要-トランザクション
• ビットコインの概要-プロトコル
• 一言で言えばビットコイン-ブロックチェーン
• ビットコインの概要-マイニング

目次

1. はじめに
2. 楕円曲線
3. デジタル署名
4. 秘密鍵
5. 公開鍵
6. フォーマットと住所
7. サイン
8. 確認する
9. 書式
10. リンク集

はじめに

上で言ったように、暗号化はビットコインの基本的な部分です。 それがなければ、何も機能しなかったので、ここから始める必要があります。

ビットコインは、 楕円曲線のいわゆる暗号化 （ 楕円曲線暗号化、ECC ）を使用します。 特別な機能に基づいています-楕円曲線（楕円と混同しないでください）。 この機能とは何か、そしてなぜそれが非常に注目に値するのかをさらに説明します。

楕円曲線

フィールド上の楕円曲線 上の射影平面上の非特異3次曲線 （フィールドの代数的閉包 ）フィールドからの係数を持つ次数3の方程式で定義 および「無限大を指す」- ウィキペディア

指の場合、楕円曲線は外向きにかなり単純な関数であり、通常、いわゆるワイエルシュトラス型の形式で記述されます。

パラメータ値に応じて そして 、この関数のグラフは異なって見える場合があります。



Pythonでグラフをレンダリングするためのスクリプト：

import numpy as np import matplotlib.pyplot as plt def main(): a = -1 b = 1 y, x = np.ogrid[-5:5:100j, -5:5:100j] plt.contour(x.ravel(), y.ravel(), pow(y, 2) - pow(x, 3) - x * a - b, [0]) plt.grid() plt.show() if __name__ == '__main__': main() 

Wikiを信じるなら、初めてこの機能がディオファントスの著作でライトアップされ、その後17世紀にニュートン自身がそれに興味を持つようになりました。 彼の研究は多くの点で、楕円曲線上の点を追加するための公式を導きました。 ここと下で、楕円曲線を考えます 。

2つの点があります 。 彼らの合計はポイントと呼ばれます 、最も単純な場合では、次のように定義されます。 そして -彼女は曲線を横切る 一点で彼女に電話しましょう 。 変わる 点座標 サインの反対側に、ポイントを取得します 、これを合計と呼びます そして それは 。



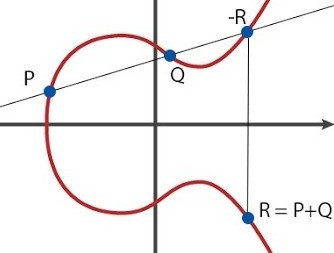
私たちはそのような加算操作を導入していることに注意する必要があると思います-通常の意味でポイントを追加する場合、つまり対応する座標を追加する場合、あなたは完全に異なるポイントを取得します 、ほとんどの場合、何の関係もありません または 曲線上にはまったくありません 。

最も賢い人はすでに質問を自問しています-たとえば、フォームの座標を持つ2つの点を通る直線が描かれた場合、どうなりますか そして 、つまり、それらを通る線は縦座標軸（下図の3番目のフレーム）と平行になります。



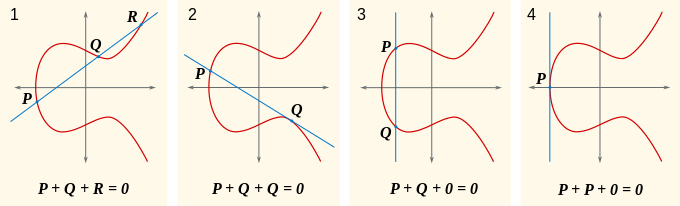
この場合、曲線と3番目の交差点がないことが簡単にわかります。 私たちが呼んだ 。 この事件を避けるために、通常無限大と呼ばれるいわゆる無限遠点を導入します または単に 写真のように。 そして、我々は交差点がないと言います 。

特に興味深いのは、ポイントを自分自身に追加したい場合です（2フレーム、1ポイント ） この場合、単に点に接線を引きます に関して得られた交点を反映します 。

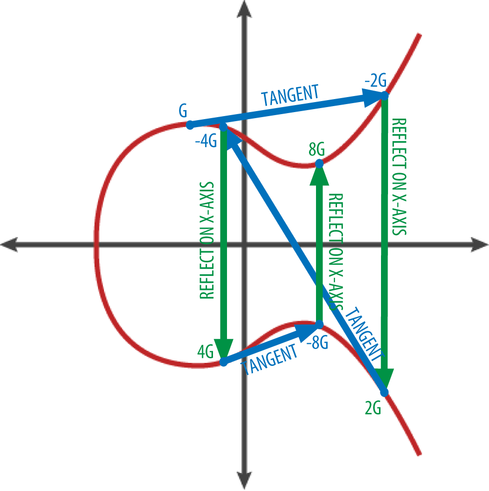
さて、手首を軽くたたくと、ポイントを数倍する操作に入ることができます 数。 その結果、新しいポイントを獲得します それは 回。 写真ですべてが明らかになるはずです。

有限体上の楕円曲線

ECCは、正確に同じ曲線を使用しますが、有限フィールドでのみ考慮されます 素数です。 それは

このような関数の名前付きプロパティ（加算、乗算、無限遠点）はすべて有効なままですが、この関数を描画しようとすると、おなじみの楕円曲線にしか似ていません（せいぜい）。 また、「ある点での関数に接する」という概念は、一般にすべての意味を失いますが、それは大丈夫です。 以下は関数の例です のために ：



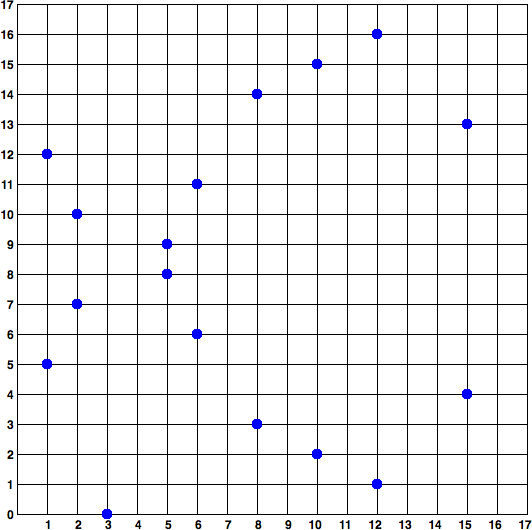
しかし、 、一般にほぼ混oticとしたポイントのセットがあります。 このグラフの起源を思い出させる唯一のものは、軸についての対称性です 。



PS有限体上の曲線の場合のように興味がある場合は、点の座標を計算します 座標を知る そして -N. Mistryによる「ビットコイン、楕円曲線、およびECDSAの数学入門」を参照してください。すべてが詳細に記載されており、8年生レベルの数学を知っているだけで十分です。

PPS私の例があなたの探究心を満たさなかった場合、ここにあらゆる種類の曲線を描くためのサイトがあります 、実験。

SECP256k1

ビットコインに戻ると、 SECP256k1曲線を使用します。 彼女の形は フィールド上で表示 どこで -非常に大きな素数、すなわち 。

いわゆるベースポイントはSECP256k1にも定義されています。これはジェネレータポイントでもあります -それは単なるポイントであり、通常は この曲線の上に横たわる。 以下で説明する公開鍵を作成する必要があります。

簡単な例：Pythonを使用して、ポイントが属しているかどうかを確認します SECP256k1カーブ

 >>> p = 115792089237316195423570985008687907853269984665640564039457584007908834671663 >>> x = 55066263022277343669578718895168534326250603453777594175500187360389116729240 >>> y = 32670510020758816978083085130507043184471273380659243275938904335757337482424 >>> (x ** 3 + 7) % p == y**2 % p True 

デジタル署名

電子署名（EDS）、電子デジタル署名（EDS）-秘密署名キーを使用した情報の暗号変換の結果として取得され、署名が生成された瞬間から電子文書に情報の歪みがないことを検証できる電子文書の詳細（整合性）、署名は鍵証明書の所有者に属します署名（著者）、および検証に成功した場合は、電子文書への署名（否認防止）の事実を確認します- ウィキペディア

一般的な考え方は次のとおりです。アリスは1 BTCをボブに転送したいと考えています。 これを行うために、彼女は次のようなメッセージを作成します。

 { "from" : 1FXySbm7jpJfHEJRjSNPPUqnpRTcSuS8aN, // Alice's address "to" : 1Eqm3z1yu6D4Y1c1LXKqReqo1gvZNrmfvN, // Bob's address "amount" : 1 // Send 1 BTC } 

次に、アリスは彼女の秘密鍵（今のところ、これはアリスだけが知っている数字であると仮定できます）、メッセージハッシュ、および次の形式の関数を受け取ります。 。 出力で、彼女はメッセージの署名を受け取ります-ECDSAの場合、整数のペアになります。他のアルゴリズムでは、署名は異なって見える場合があります。 その後、彼女はすべてのネットワーク参加者に初期メッセージ、署名、および公開鍵を送信します。

その結果、各Vasyaは、必要に応じて、この三位一体をとることができます。 秘密鍵の所有者が実際にこのメッセージに署名したかどうかを確認します。 そして、ネットワーク内で誰もが知っている場合 アリスが所有しているので、彼女がお金を送ったのか、誰かが彼女に代わってそれをやろうとしているのかがわかります。



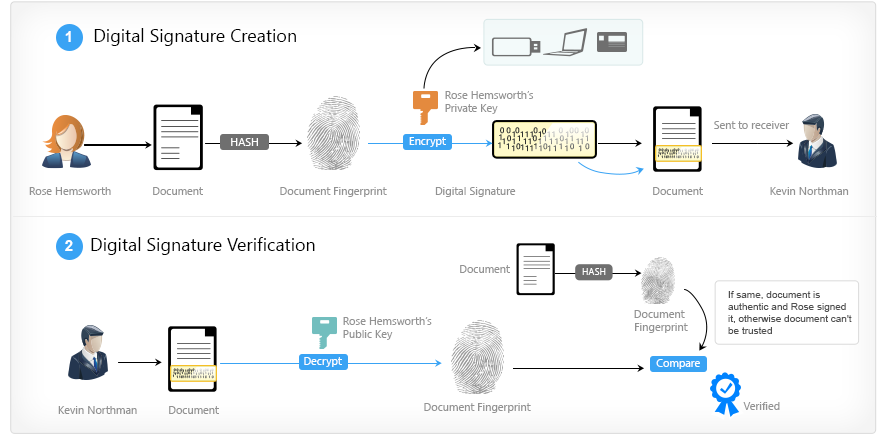
さらに、アリスとネットワークの他の部分の間に人が立っていると仮定します。 彼にアリスのメッセージを傍受させて、文字通り10億のうち1ビットを変更させます。 しかし、この場合でも、署名の検証 メッセージが変更されたことを示します。

ネットワークが分散されているため、これはビットコインにとって非常に重要な機能です。 私たちの取引が1000 BTCを譲渡する要求で誰が得るかを事前に知ることはできません。 ただし、トランザクションはあなたの秘密鍵によって署名され、他のネットワーク参加者はここで何かが間違っていることをすぐに理解するため、彼はそれを変更できません（たとえば、受信者として自分のアドレスを示します）。

AHTUNG！ 実際、プロセスは上記とはまったく異なります。 ここでは、電子デジタル署名とは何か、なぜ必要なのかを指で示しました。 実際のアルゴリズムは、 「Bitcoin in a nutshell-Transactions」の章で説明されています。

秘密鍵

秘密鍵はかなり一般的な用語であり、さまざまな種類の秘密鍵をさまざまな電子署名アルゴリズムで使用できます。

お気づきかもしれませんが、ビットコインはECDSAアルゴリズムを使用しています-その場合、秘密キーは256ビットの自然な数値、つまり、 前に 。 技術的には、 123456という数字でも有効な秘密キーになりますが、攻撃者が秘密キーを手に入れるまで、コインはすぐに「所属」し、 123456のような値は非常に簡単に見つかります。

今日では、すべてのキーを並べ替えることは不可能であることに注意することが重要です -これは驚くほど多数です。

私たちはそれを提示しようとします： この記事によると、地球全体では少し少ない 砂粒。 という事実を活用してください それは 砂粒。 そして、私たちはすべてのアドレスを持っています およそ 。

これは、地球上のすべての砂を取り、すべての砂粒を新しい地球に、結果として生じる惑星の山で、各惑星上のすべての砂粒を新しい地球に変えることができ、砂粒の総数が依然として可能な秘密鍵の数よりも数桁少ないことを意味します。

同じ理由で、秘密鍵を作成するとき、ほとんどのビットコインクライアントは単に256のランダムビットを取得します-衝突の可能性は非常に小さいです。

Python

 >>> import random >>> private_key = ''.join(['%x' % random.randrange(16) for x in range(0, 64)]) >>> private_key '9ceb87fc34ec40408fd8ab3fa81a93f7b4ebd40bba7811ebef7cbc80252a9815' >>> # or >>> import os >>> private_key = os.urandom(32).encode('hex') >>> private_key '0a56184c7a383d8bcce0c78e6e7a4b4b161b2f80a126caa48bde823a4625521f' 

Python、 ECDSA

 >>> import binascii >>> import ecdsa # sudo pip install ecdsa >>> private_key = ecdsa.SigningKey.generate(curve=ecdsa.SECP256k1) >>> binascii.hexlify(private_key.to_string()).decode('ascii').upper() u'CE47C04A097522D33B4B003B25DD7E8D7945EA52FA8931FD9AA55B315A39DC62' 

Bitcoin-cli

 $ bitcoin-cli getnewaddress 14RVpC4su4PzSafjCKVWP2YBHv3f6zNf6U $ bitcoin-cli dumpprivkey 14RVpC4su4PzSafjCKVWP2YBHv3f6zNf6U L3SPdkFWMnFyDGyV3vkCjroGi4zfD59Wsc5CHdB1LirjN6s2vii9 

公開鍵

させる -秘密鍵、 -基点、次に公開キー 。 つまり、実際には、 公開鍵は曲線SECP256k1上にある特定のポイントです。

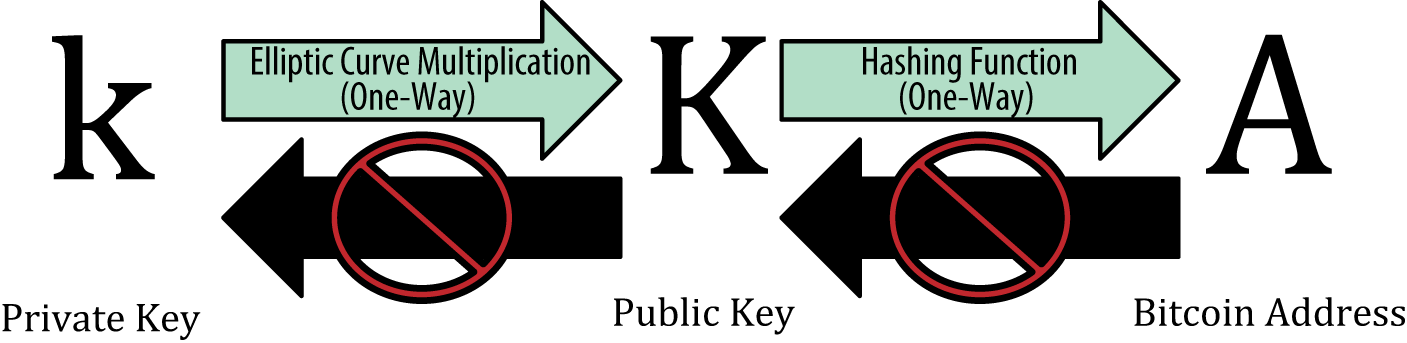
2つの重要なニュアンス。 まず、公開鍵を取得する操作が一意に決定されること、つまり、単一の秘密鍵が常に単一の公開鍵に対応することは容易にわかります。 第二に、逆の操作は計算上困難であり、一般的な場合、公開キーから秘密キーを取得することは、最初の完全な検索によってのみ可能です。

以下では、公開鍵とアドレスの間にまったく同じ関係が存在することがわかります。全体のポイントは、ハッシュ関数が不可逆的であることです。

Python、ECDSA

 >>> import binascii >>> import ecdsa >>> private_key = ecdsa.SigningKey.generate(curve=ecdsa.SECP256k1) >>> public_key = private_key.get_verifying_key() >>> binascii.hexlify(public_key.to_string()).decode('ascii').upper() u'D5C08F1BFC9C26A5D18FE9254E7923DEBBD34AFB92AC23ABFC6388D2659446C1F04CCDEBB677EAABFED9294663EE79D71B57CA6A6B76BC47E6F8670FE759D746' 

C ++、 libbitcoin

 #include <bitcoin/bitcoin.hpp> #include <iostream> int main() { // Private key bc::ec_secret secret = bc::decode_hash( "038109007313a5807b2eccc082c8c3fbb988a973cacf1a7df9ce725c31b14776"); // Get public key bc::ec_point public_key = bc::secret_to_public_key(secret); std::cout << "Public key: " << bc::encode_hex(public_key) << std::endl; } 

コンパイルして実行するには、（libbitcoinの事前インストール）を使用します。

 $ g++ -o public_key <filename> $$(pkg-config --cflags --libs libbitcoin) $ ./public_key Public key: 0202a406624211f2abbdc68da3df929f938c3399dd79fac1b51b0e4ad1d26a47aa 

最初と2番目の例の公開キーの形式が異なる（少なくとも長さが）ことがわかります。これについては、以下で詳しく説明します。

フォーマットと住所

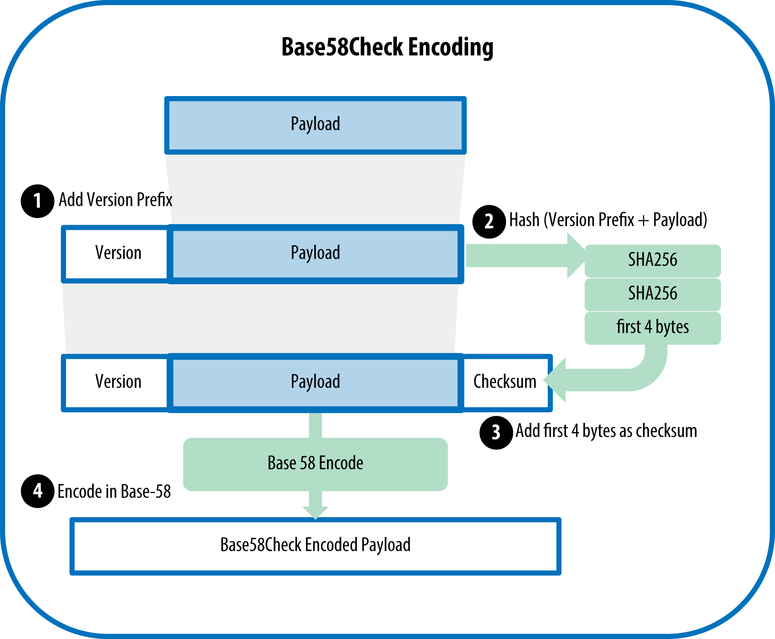
Base58Checkエンコーディング

このエンコーディングは本全体で絶えず遭遇するため、どのように機能するのか、なぜ必要なのかを理解する必要があります。

その本質は、バイトシーケンスを最も読みやすい形式でできるだけ短く書き留めると同時に、タイプミスの可能性をさらに低くすることです。 Bitcoinの場合、セキュリティは決して不要ではないことをご理解いただいていると思います。 1つの間違ったキャラクターとお金が、おそらく誰も見つけられないキーにアドレスに行きます。 base58.hからのこのエンコーディングに関するコメントは次のとおりです。

 // Why base-58 instead of standard base-64 encoding? // - Don't want 0OIl characters that look the same in some fonts and // could be used to create visually identical looking account numbers. // - A string with non-alphanumeric characters is not as easily accepted as an account number. // - E-mail usually won't line-break if there's no punctuation to break at. // - Doubleclicking selects the whole number as one word if it's all alphanumeric. 

記録の簡潔さは、かなり一般的なBase64エンコードを使用して実装するのが最も簡単です。つまり、数字0,1,...,9 、文字azおよびAZが書き込みに使用されるbase 64番号システムを使用します-これは62文字を与え、残りの2つは実装によって異なります。

Base58Checkの最初の違いは、文字0,O,l,I 、誰かが混同することにした場合に備え0,O,l,I削除されることです。 58文字であることがわかります。

 b58 = '123456789ABCDEFGHJKLMNPQRSTUVWXYZabcdefghijkmnopqrstuvwxyz' def base58encode(n): result = '' while n > 0: result = b58[n%58] + result n /= 58 return result # print "Base58 encode for '123123':", base58encode(123123) # # Base58 encode for '123123': dbp 

2番目の違いは同じチェックです。 行の最後に、 チェックサムが再び追加されますSHA256(SHA256(str))最初の4バイトSHA256(SHA256(str)) 。 また、base58でのエンコードの前に先行ゼロがあったのと同じ数のユニットを先頭に追加する必要があります。これはすでに技術的な問題です。

 import hashlib def base58encode(n): b58 = '123456789ABCDEFGHJKLMNPQRSTUVWXYZabcdefghijkmnopqrstuvwxyz' result = '' while n > 0: result = b58[n % 58] + result n /= 58 return result # Will be used to decode raw bytes and then encode them to the base58 def base256decode(s): result = 0 for c in s: result = result * 256 + ord(c) return result def countLeadingZeroes(s): count = 0 for c in s: if c == '\0': count += 1 else: break return count def base58CheckEncode(prefix, payload): s = chr(prefix) + payload checksum = hashlib.sha256(hashlib.sha256(s).digest()).digest()[0:4] result = s + checksum return '1' * countLeadingZeroes(result) + base58encode(base256decode(result)) 

秘密鍵の形式

秘密鍵を保存する最も明白な方法は、256ビットをゼロと1の束として書き込むことです。 しかし、おそらく、技術的に有能な人なら、同じシーケンスを32バイトの形式で提示する方がはるかに簡単であることを理解しています。各バイトは16進表記の2文字に対応します。 この場合、数字0,1,...,9と文字A,B,C,D,E,Fいることを思い出させてください。 上記の例ではこの形式を使用しましたが、美しさのためにスペースで区切られている場合があります。

 E9 87 3D 79 C6 D8 7D C0 FB 6A 57 78 63 33 89 F4 45 32 13 30 3D A6 1F 20 BD 67 FC 23 3A A3 32 62 

もう1つのより高度な形式は、 WIF （ Wallet Import Format ）です。 それは非常に簡単に構築されます：

1. 0C28FCA386C7A227600B2FE50B7CAE11EC86D3BF1FBE471BE89827E19D72AA1Dなどの秘密鍵を取得します
2. プレフィックス0x80付けてBase58Checkに書き込みます。 それだけです

 private_key = '0a56184c7a383d8bcce0c78e6e7a4b4b161b2f80a126caa48bde823a4625521f' def privateKeyToWif(key_hex): return base58CheckEncode(0x80, key_hex.decode('hex')) # print "Private key in WIF format:", privateKeyToWif(private_key) # # Private key in WIF format: 5HtqcFguVHA22E3bcjJR2p4HHMEGnEXxVL5hnxmPQvRedSQSuT4 

公開鍵形式

念のため、公開キーはSECP256k1行の単なるポイントであることを思い出させてください。 これを記述する最初で最も一般的なバリアントは、XおよびY座標ごとに32バイトの非圧縮形式です。 混乱を避けるために、プレフィックス0x04とその65バイトが使用されます。

 import ecdsa private_key = '0a56184c7a383d8bcce0c78e6e7a4b4b161b2f80a126caa48bde823a4625521f' def privateKeyToPublicKey(s): sk = ecdsa.SigningKey.from_string(s.decode('hex'), curve=ecdsa.SECP256k1) vk = sk.verifying_key return ('\04' + sk.verifying_key.to_string()).encode('hex') uncompressed_public_key = privateKeyToPublicKey(private_key) # print "Uncompressed public key: {}, size: {}".format(uncompressed_public_key, len(uncompressed_public_key) / 2) # # Uncompressed public key: 045fbbe96332b2fc2bcc1b6a267678785401ee3b75674e061ca3616bbb66777b4f946bdd2a6a8ce419eacc5d05718bd718dc8d90c497cee74f5994681af0a1f842, size: 65 

ただし、名前が示すように、これは公開鍵を保存する最良の方法ではありません。

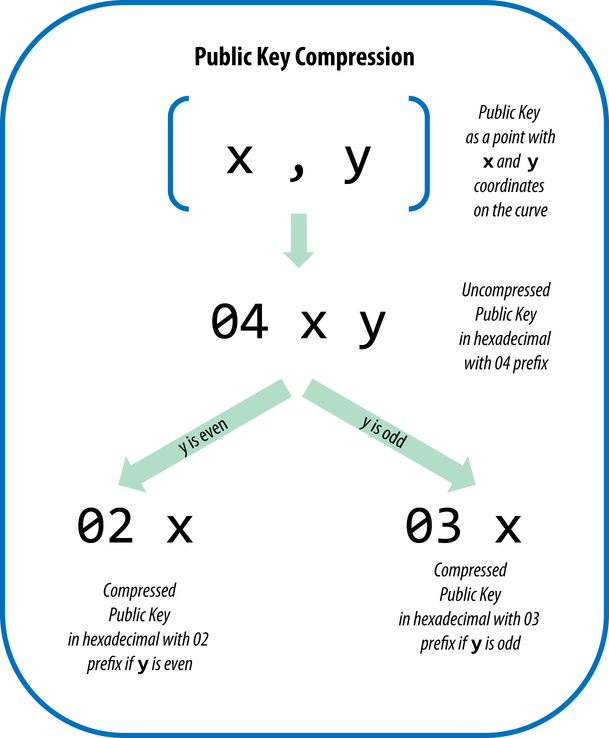
驚くでしょうが、2番目の形式は圧縮と呼ばれます。 その本質は次のとおりです。公開鍵は曲線上の点、つまり式を満たす数値のペアです 。 したがって、X座標のみを記述でき、Y座標が必要な場合は方程式を解くだけです。 したがって、公開キーのサイズをほぼ50％削減します！

唯一の注意点は、ポイントが曲線上にある場合、X座標のこの方程式には明らかに2つの解決策があることです（疑わしい場合は上のグラフを見てください）。 通常、Y座標の符号を保持しますが、有限体上の関数に関しては、次のプロパティを使用する必要があります： X座標の方程式の解がある場合、ポイントの1つは偶数のY座標を持ち、2番目のポイントは奇数の座標 （再びあなた自身で見ることができます）。

最初のケースでは、プレフィックス0x02れ、2番目のケースでは0x03 0x02ます。 プロセスの例を次に示します。

住所

すでに述べたように、アドレスは公開キーから独自の方法で取得されます。 さらに、暗号的に強力なハッシュ関数-RIPEMD160およびSHA256が使用されているため、逆の操作を実行することはできません 。 公開鍵をアドレスに変換するアルゴリズムは次のとおりです。

1. 45b0c38fa54766354cf3409d38b873255dfa9ed3407a542ba48eb9cab9dfca67などの秘密鍵を45b0c38fa54766354cf3409d38b873255dfa9ed3407a542ba48eb9cab9dfca67
2. 非圧縮形式で公開鍵を取得します。この場合は04162ebcd38c90b56fbdb4b0390695afb471c944a6003cb334bbf030a89c42b584f089012beb4842483692bdff9fcab8676fed42c47bffb081001209079bbcb8dbです。
3. RIPEMD160(SHA256(public_key))を考慮すると、 RIPEMD160(SHA256(public_key))であることが5879DB1D96FC29B2A6BDC593E67EDD2C5876F64C
4. 結果を接頭辞17JdJpDyu3tB5GD3jwZP784W5KbRdfb84Xます。 これは住所です。

 def pubKeyToAddr(s): ripemd160 = hashlib.new('ripemd160') ripemd160.update(hashlib.sha256(s.decode('hex')).digest()) return base58CheckEncode(0, ripemd160.digest()) def keyToAddr(s): return pubKeyToAddr(privateKeyToPublicKey(s)) # print keyToAddr("45b0c38fa54766354cf3409d38b873255dfa9ed3407a542ba48eb9cab9dfca67") # # '17JdJpDyu3tB5GD3jwZP784W5KbRdfb84X' 

署名と検証

ECDSAがメッセージをどのように署名およびチェックするかについての技術的な詳細を知る必要はないと思います。とにかく、どこでも既製のライブラリを使用します。 主なことは、なぜこれが必要なのかについて共通の理解を持っていることですが、まだ興味がある場合は、 楕円曲線デジタル署名のレイマンのガイドをご覧ください。以下のプロセス全体の美しい視覚化があり、自分で試してみることができます。

次の章、 Bitcoin in a nutshell-Transactionです。

リンク集

• 「ビットコイン、楕円曲線、ECDSAの数学入門」N.ミストリー
• Di Wangによる「ビットコインでのECDSA署名の安全な実装」
• 楕円曲線暗号：優しい紹介
• 楕円暗号：理論
• ビットコイン秘密鍵とアドレスの生成