みなさん、こんにちは、もう1つの分析の準備ができています。 今日はレポートをJPointで見るのではなく、DotNextで見ることにします! レポートの著者はAndrey
DreamWalker Akinshinであり、彼のプレゼンテーションは.NETでの浮動小数点演算の実装の詳細に専念しています。
スライドは
こちらにあります 。
免責事項:算術の実装については、記事自体ではなく、解析されたレポート自体のみ。
プロット
この時点で、私はパズルのピースがあまり好きではないと言わなければなりません。 それらは仕様の暗いコーナーの知識を必要としますが、実際には通常は役に立ちません。 あなたがなぞなぞの恋人によって書かれたコードを伴うと想像してください。
「方法」を伝える前に重要なことを考えさせるのは一般的に良いことであることに注意してください。彼は結果をずっとよく覚えているでしょう。 しかし、本質から始めること、つまり、人々に伝える必要がある知識を選択し、それを単純な条件で逆説的なタスクで説明することは困難です。 パズルを覚えるのにそれほど重要ではないが、誰もそれらを知らないものを取り上げ、純粋な娯楽にすることは、しばしばパズルを解く人にとって簡単です。
一般的に、注意深い読者であれば、この記事のジャンルに対する私の嫌悪を簡単に追跡できます。
物語の動きと演技
ここには矛盾があります。アシスタントが競争の幻想を作り出すために現場にやって来ますが、タスク間の答えと移行の発言が事前に知られていることは明らかです。 たとえば、12:00-12:20にジュリアは、全体へのキャストは適切な操作ではないと主張し、丸めを使用する必要があります。次に、丸めのために次のタスクが表示されます。 そのような状況では、アシスタントの「頭に来た」と思われるトピックがすぐにではなく、少し後に発生するように、タスクの順序を変更します。 信頼性を高めるために、アシスタントは互いに同意する場合があります。
また、私にはアンドレイ・ドミトリエフの不幸なカメオ(39:00)のようです。 次のDotNextと次のレポートを宣伝するために、このスケッチが必要な理由は明らかです。 しかし、時間がなくなったと言っているので、まだ問題はありますが、すべてが真実であるかのように見せてください。 第一に、「かろうじて」話すことで、質問に答える時間がもう少しあるとは言わない。 次に、2つまたは3つの追加のタスクを回答で強調表示し、中断時にスライドをスクロールします。 そうすると、人々は興味を持ち、突然Zeigarnik効果が働き、プレゼンテーションがダウンロードされ、誰もが大丈夫です。
それで、私は当惑したままでした:それは何についてですか? 一体型...
方法だけでなく、なぜ
一部の場所では、仕様の開発者が何を吸ったのか正確に理解していませんでした。 なぜ彼らはちょうどそれをしましたか? これは、覚えやすくするだけでなく、ランダムなナンセンスから重要なタスクを分離するのにも役立ちます。 たとえば、前述の丸め(12:20から開始)を見てみましょう。

最も近いものへの丸めはどこから来たのですか? デフォルトでオンになっているのはなぜですか? 「ゼロから離れる」モードはいつ必要ですか? たぶん私はすべてを逃しただけで、普通の人は長い間知っていましたが、私の人生で初めてこの分析の準備でこの質問を理解しました。 政権は「銀行の丸め」と呼ばれ、主に小数部分にセント/コペックでお金を追加する必要がある場合に考案されたことがわかります。 100種類のセントしかないため、金額のランダムなセットでは、正確に50セントのテールが頻繁に発生します。 それらのすべてがゼロから四捨五入される場合、系統誤差を累積し、最も近い偶数にある場合、四捨五入誤差は平均して約ゼロになります。 さらに、特定の各数値は決定論的に丸められ、ランダムな方向ではありません(つまり、このようなアプローチ)。
多くの理由でfloatとdoubleを使用してお金を数える必要がないため、デフォルト設定は非論理的に見えます。 しかし、少なくともその背後にあるものは明らかです。 そして、誰かが銀行の丸めを使用するための別の現実的なシナリオを知っている場合は、共有してください。
仕様の背後にあるロジックを上げて、それを聴衆に伝えるのは良いことだと思います。 事実だけでなく、その原因も覚えておくと、はるかに便利です。
さて、プレゼンテーションにあったものの、演習8(17:23から)の操作の真理値表を覚えているのは誰ですか?
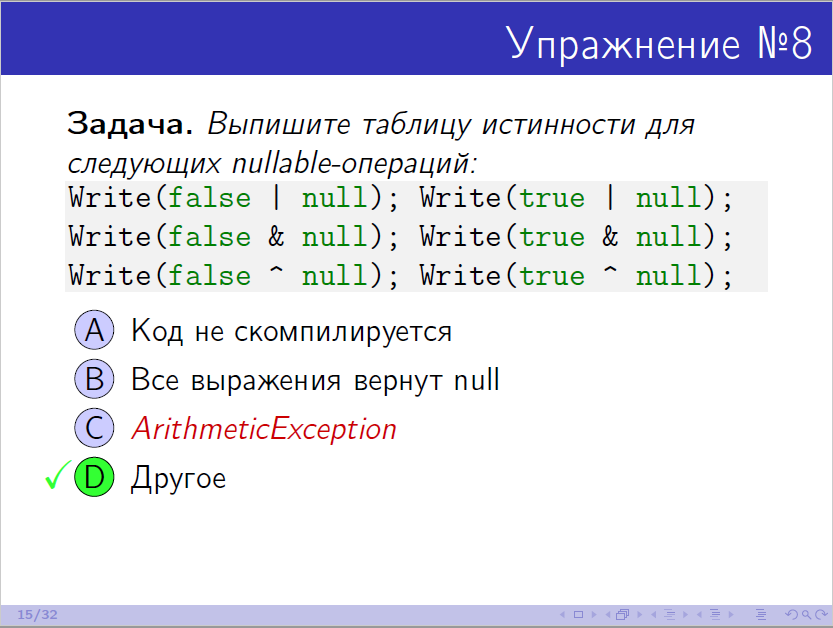
一般的に知ることは重要ですか? 開発者が念頭に置いた使用シナリオを理解していれば、復元する方が簡単です。
それどころか、演習10の関連性を疑問視することはできません(21:18から):
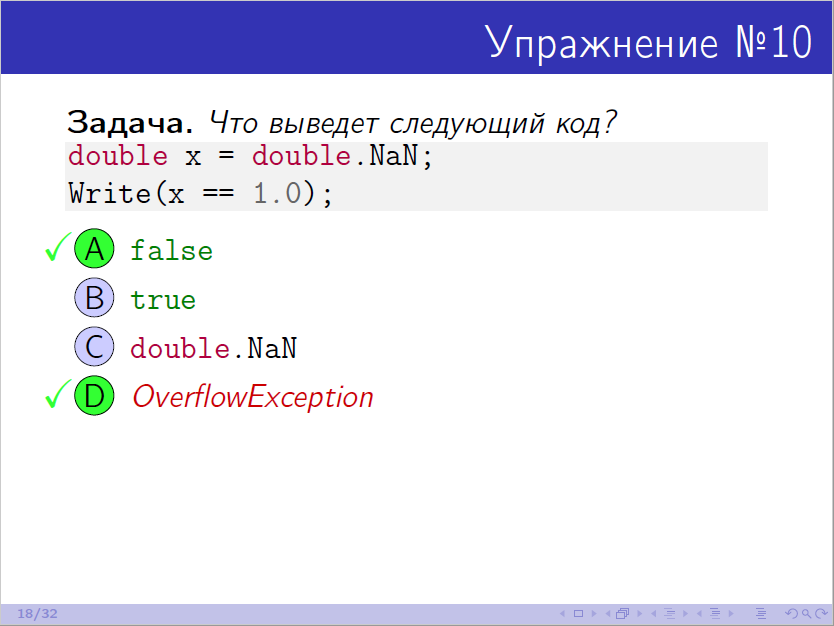
Andreyは、OverflowExceptionで問題を踏むことができる状況について語り、より慎重になりたいという楽観的な願望で物語を終わらせます。 誰もがより注意を払う方法をすぐに理解しましたか? 詳細は邪魔になりません。
フロートの仕組み
もちろん、大学では、データの表示に専念するコースの断片、またはコース全体もありました。 そしてもちろん、そこで浮動小数点数について話されましたが、多くのことは実践せずに忘れられます。 一部のタスクでは、Andreiは、floatやdoubleなどの基本的なプロパティと、それらから生じる問題に触れますが、これに視聴者の注意を集中させることはありません。 最も顕著な例は、結合性の問題です(運動14、31:30から):

ホールの全員が正解したわけではないことを考えると、最初または2番目のコースの資料を更新する必要があります。 この場合、数値が不均一に分布していることが重要です。ゼロから離れるほど、数値の間隔が大きくなります。 最大次数の2つの隣接するフロートを見てみましょう(ダブルは同じ意味で、さらに多くを描画します)。


問題の形式の観点からは、それらの間に何もありません。 さらに、現実の世界では、最初の数値は1.7014122 * 10
38であり、2番目の数値は1.701412 * 10
38であり、それらの差は0.0000002 * 10
38です。 これは、慎重に言ってみましょう。 最大次数に1、1000、または10億を追加することは不可能です。
この仕組みを知っていると、連想のルールがどのように違反されているかを理解するのは簡単です:いくつかの小さな数字の合計は、2つの隣接する大きな数字の間の距離よりも大きくなることがあります。
結論
一般的に、各パズルゲームは、聴衆の注意をスピーカーの信用に与える魅力的なストーリーであり、この信用を使用して、少なくともいくつかの謎から道徳を引き出すことができます(実際にはそこにあります!)。 私は、レポートがこれから利益を得ると確信しています。
スライド
スライドはよくできているので、ささいなことで欠点を見つけることはしませんが、模倣に値する決定に注意します。
スライド要素のシーケンシャルな外観
レポートには、多くの情報を含む多くのスライドがあります。 画面上のすべてをすぐに理解して理解することは困難ですが、アンドレイの要素が順番に表示されます。 したがって、視聴者は、あなたが見なければならない場所をいつでも失うことはなく、話し手は話している。 これにより、大きなスキーム、コード、リストの認識が大幅に促進されます。 アンドリューとしてやってください。
均一性
プレゼンテーションには、ホメロスシンプソン(原則として、より良い解像度で探すことができる)と不可欠なものを除いて、面白い写真はほとんどありません。 数学自体は楽しいです。
同時に、各エクササイズは同じ方法で設計され、ソリューションは同じように強調表示され、説明はスライドのタイトルにマークされます-視聴者はすぐに慣れ、パズルを解くのを邪魔するものはありません。 小規模なプレゼンテーションが多数ある場合は、この場合のように、同様のレイアウトに固執することは理にかなっています。
定期的なレビュー
プレゼンテーションに関するフィードバックを受け取りたい場合は、喜んで提供します。
これには何が必要ですか?- スピーチのビデオへのリンク。
- スライドへのリンク。
- 著者からの申請。 スピーカー自身の同意がなければ、何も分析しません。
これはすべて、p0b0rchy
habrayuzer 、つまり私に送信する必要があります。 レビューは建設的で丁寧であり、改善が必要なものだけでなく、肯定的な側面を強調することを約束します。