子供としてプロローグに書いていない人には心がなく、今日書いている人には頭がありません。 （ オリジナル ）

あなたが常に苦痛の疑いに苦しめられているなら、この論理プログラミング（LP）はどんな種類のゴミであり、一般にそれが必要なのですか？ 次に、この記事はあなたのためです。

たとえば、次のように、プログラミング言語をさまざまな方法でグループに分けることができます（多くの場合、プログラミングパラダイムと呼ばれます）。

• 構造 ：プログラムはブロックに分割されます-サブプログラム（互いに分離）、および主な制御要素は一連のコマンド、分岐、およびループです。
• オブジェクト指向 ：タスクは、相互にメッセージを送信するオブジェクトとしてモデル化されます。 オブジェクトにはプロパティとメソッドがあります。 抽象化。 カプセル化。 多型。 まあ、一般的に、誰もが知っています。
• functional ：基本要素は関数であり、タスク自体は関数としてモデル化されます。あるいは、f（。）とg（。）が関数である場合、f（g（。））構成。
• 論理的 ：ここでは、原則として、贅沢が始まります-最初の3つについて何百もの記事、書籍、レビュー、プレゼンテーション、および教科書が書かれている場合、ここでせいぜいプロローグとピンクフロイドとプロコルハルム時代の発展について見ます（少なくとも、彼らはそのとき音楽で幸運だった）、それが物語の終わりです。

ここで、この間違いを修正します。

この記事の最も重要な論文：

論理プログラミング！=プロローグ。

一般に、後者はおそらく必要ありません。 しかし、最初はそうかもしれません。

記事の構造 ：

• プロローグとは何で、なぜそれを必要としないのか
• なぜ必要なのか、回答セットプログラミングの簡単な紹介
• ASPでタスクを解決します
• 組み合わせ最適化
• 確率的LP：ProbLog
• クラシックロジックFO上のLP（。）およびIDP
• スケッチ回答セットのプログラミング
• 実験分析
• プログラムのテストと正確さ
• おわりに

この記事は（おそらく）ロシア語で初めて、現代の論理プログラミングの主要な側面を、それらがなぜ必要なのかを説明します。 論理プログラミング（LP）は、博士号のテーマに直接関連しています（詳細については、別の詳細な投稿があります）。 その過程で、ロシア語には実質的に資料がないことに気付き、このギャップを埋めることに決めました（ロシアのウィキペディアには、書く価値のあるASPに関する記事すらありません）。

記事の一部は、SketchingやProblogなど、互いに直接関連していない場合があります。ある意味では、これは論理プログラミングの分野で最も興味深いトピックと開発の個人的な概要です。 ここでは、もちろん、薬物に関連するすべてのトピックをカバーすることはできませんが、関心のある読者がトピックに飛び込むか、薬物がそのような動物であると想像するための最初のステップであると考えることができます。

プロローグとは何で、なぜそれを必要としないのか

Prolog（Logicのプログラミング、元はprogrammation en logique）は、70年代初頭にAlain Colmeroeによってマルセイユで開発されました。 この言語の基礎は、ホーンの論理式（つまり、どれだけ正確にそれらを機械加工できるか）のステートメントの手続き上の解釈です：

a :- b, c, d,...,z. 

読み方は、「条件b、c、d、...、zが満たされている場合、それから」である必要があります。

そして、簡単に言えば（ここではすべての技術的な詳細を省略しています）、論理的なシーケンスの形式で書き直すことができます。

実際、ボブ・コワルスキーirは次のことを思いつきました。「a」という文は、その前提がすべて真実であることを証明すれば真実です。 （ちなみに、優秀で元気な男はまだ元気で、ジョークや物語をふりかけています.1年前にロンドンのロイヤルコミュニティでの会議で、彼はPrologと論理プログラミングの歴史について素晴らしい素晴らしい講演をしました。）

塩とは何ですか、コワルスキー？ 「a：-b、c、d」という表現を使用すると、次のようになります。

「a」は、「b」を証明し、「c」を証明し、「d」を証明することができれば真実です。

それから、各プログラムはステートメントの派生のための定理のセットであり、各表現は「証明」されます（注意深い読者はここでカリー-ハワード同型に確かに気づくでしょう ）。

ここで否定を追加すると、タスクはもう少し楽しくなります。 Prologでは、失敗として否定と呼ばれ、ロジックの古典的な否定とは異なります。 理論的には、次のように聞こえます。「a」というステートメントを証明できなかった場合、それは間違っていることを意味します。 ロジックでは、このような仮定は閉じた世界の仮定と呼ばれ、時には非常に意味があります。

失敗としての否定と閉じた世界の仮定

サマラ市の11番目のルートのバスのスケジュールを想像してください、フラグメント：

• 15:15
• 15:45
• 16:15
• 16:45
• 17:15

質問：16:00にバスはありますか？ 彼はそうではありません。なぜなら、彼がスケジュールに従っていることを証明できないからです。 スケジュールには、サマラ市の11番目のルートを歩く世界の全体像があります。 したがって、「閉じた世界の仮定」という名前-条件付きの世界全体がこのプログラムによって記述されるという仮定-外部はすべて偽です。 原則として、それはデータベースでも使用されます-ところで、私はそれらについてここに書きました 。

完全なプログラミング言語であるチューリングとしてのプロローグ

Prologのいくつかの興味深い演算子（カットなど）と一緒になります-完全な言語のチューリング-要するに-プロローグPのプログラムが関数f（x）を計算すると、f（x）を計算する他のチューリング完全言語のプログラムMがあります） したがって、Prologでプログラムを解決できる場合、他の言語（Python、Java、C、Haskellなど）でソリューションを作成できることを意味します。 ここにはチャクラは開いていません。

一般に、Prologの問題の解決策は、Bob Kowalskiに従ってスキームに分解されます。

アルゴリズム=ロジック+コントロール

プロローグで適切に定式化され解決されるタスクの良い例は、特定の条件が満たされるかどうかに応じた一連のルールです。 ただし、解決策を見つけるためのアルゴリズムを設定する必要があります。許容値のスペースはどのくらいか、バイパスされる順序などです。 本質的に、推論ルールの形式でタスクをモデル化し、推論ルールを使用して、ソリューション（ルールの順序、カット、リストの値からルールの本体からヘッドへの移行など）および許容されるソリューションスペースを見つける手順を指定します。

私のコメント、The Art Of Prologのコード（自発的な欲求がある場合） ラップを読む プロローグを勉強するには、この本をお勧めします）

 quicksort([X|Xs],Ys) :- % head: X -- pivot element, Xs -- the rest, Ys -- sorted array partition(Xs,X,Littles,Bigs), % X divides Xs into Littles = [x < X for x in Xs], and Bigs quicksort(Littles,Ls), % The smaller ones are sorted into Ls quicksort(Bigs,Bs), % Same for biggies append(Ls,[X|Bs],Ys). % Then Ys -- output is literally Ls + [X] + Bs quicksort([],[]). % empty array is always sorted partition([X|Xs],Y,[X|Ls],Bs) :- X =< Y, partition(Xs,Y,Ls,Bs). % If X an element of the given array is above Y, it goes into biggies partition([X|Xs],Y,Ls,[X|Bs]) :- X > Y, partition(Xs,Y,Ls,Bs). % else into littles partition([],Y,[],[]). % empty one is always partitioned 

クイックソートの述語は、空のリストと空でないリストの2つの場合に定義されていることがわかります。 空ではないケースに興味があります：リスト[X | Xs]が含まれます。ここで、Xはリストの先頭、つまり最初の要素（carはこのプログラムに括弧がほとんどないと思う人向け）、Xsは末尾（tail、 cdr）は、BigsとLittlesの2つのリストに分割されます-大きいものと小さいものXです。これらのリストは両方とも再帰的にソートされ、最終出力リストYsにマージされます。 一般に見られるように、推論規則を設定してアルゴリズム全体を機能させます。

良いプロローグとは何ですか？ 彼は正式なセマンティクスに優れています-つまり プロパティを正式に表示することが可能です（たとえば、上記のプログラムが実際に数値をソートすることを証明するため）、確率論的なケース（ProbLogセクションを参照）にまで拡張し、一般に、数学的な作業、メタ言語に適した論理的な問題のモデリングに便利な言語操作など。

要するに、あなたがプログラムの振る舞いの特性を正式に示す必要がある科学論文を書いていないなら、おそらくPrologは本当に必要ないでしょう。 しかし、おそらく論理プログラミングが必要ですか？

なぜ必要なのか、またはAnswer Set Programming（ASP）の簡単な紹介

ASPの簡単な説明：

SATがアセンブラーである場合、最新のASPはC ++です。

ここでは、宣言型プログラミングやジョンマッカーシー（LISPを発明し、アルゴルに影響を与え、一般に「人工知能」という用語を提案した）の精緻化許容原則などから始める価値があります。

宣言的アプローチとは何ですか？ つまり、問題とその特性について説明するものであり、解決方法については説明しません。 この場合、タスクはほとんどの場合次の形式で表示されます。

問題=モデル+検索

このアプローチはどこで定期的に会いますか？ たとえば、データベースでは、SQLは宣言型クエリ言語であり、DBMSはこのクエリに対する答えを見つける責任があります。 DBMSの効果的な操作のために数千の効果的なアルゴリズムが発明され、データは最適化された形式で格納され、インデックスはどこにでもあり、クエリ最適化方法などがあります。

しかし、最も重要なことは、ユーザーが氷山の一角であるSQL言語を見ることです。 また、DBMSについてある程度理解しているため、ユーザーは効果的なクエリを作成できます。 最初に、変化に対する抵抗の原理を簡単な例で説明しましょう。 会社の部門ごとの平均給与を計算する簡単なクエリQを作成したとします。 しばらくして、要求を少し変更するように求められました-たとえば、計算で管理を無視するために-私たちは技術専門家の平均給与に興味を持ち始めました。 この場合、条件 "role！= 'Manager'"をQクエリに追加するだけです。

したがって、新しいQ_updatedリクエストは、基本リクエスト+追加条件として表されます。 もう少し一般的に言えば、

問題のバリエーション=基本モデル+追加条件

これは、問題の条件を追加の条件Xにわずかに変更する場合、モデル（SQLなどの正式な言語で元のタスクをモデル化する）を変更し、追加の条件C_Xを追加する必要があることを意味します。

そして、ASPと論理プログラミングはどうですか？

参照：

• 多くの資料は、Torsten Schaub教授のページにあります。
• ステファン・ハルボブラーのチュートリアル
• ビデオ編集チュートリアル： into into ASP 、 ASP for Knowledge Representation
• Thomas Aiterによる優れた紹介： ASP入門書
• ASPの実践 -以前はパブリックドメインでした（現在、直接リンクは表示されていません）

PrologとASPの基本的な違いは何ですか？ 実際、ASPは制限の宣言型言語です。つまり、選択規則と呼ばれる特別な制限の形式で検索スペースを定義します。次に例を示します。

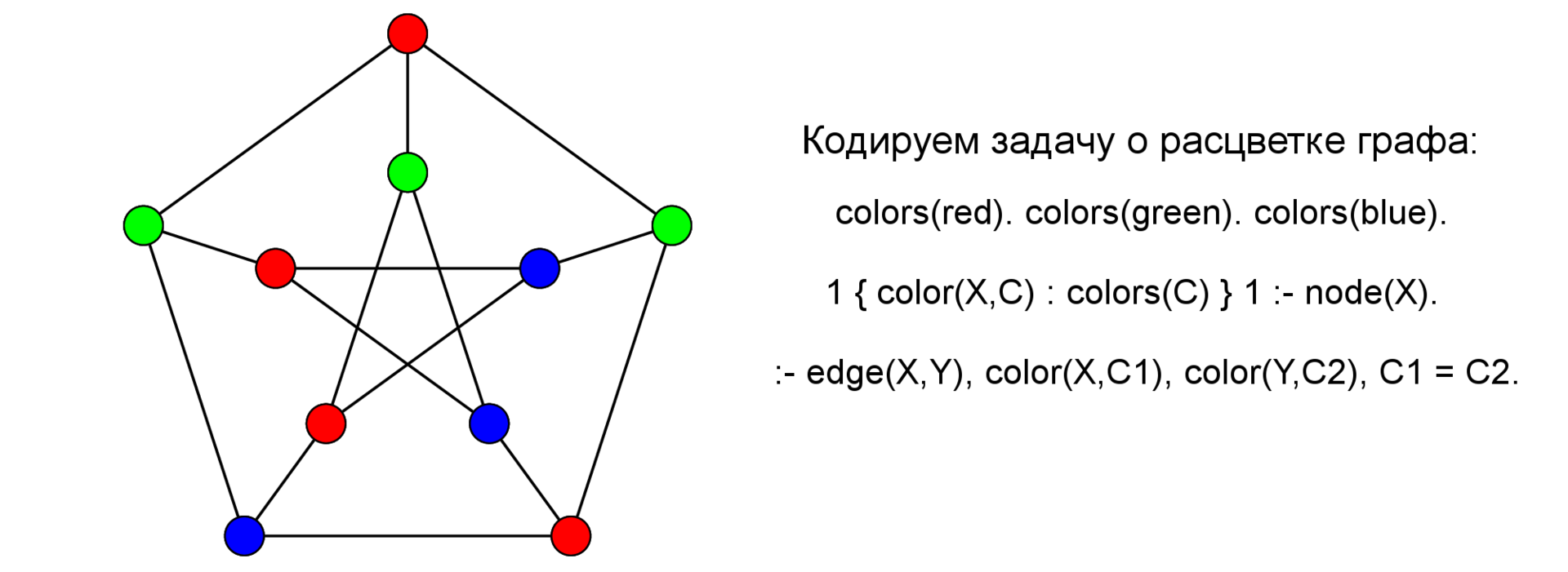
 1 { color(X,C) : colors(C) } 1 :- node(X). 

そのようなルールは列挙空間を定義します-文字通り次のように読みます：述語の各X（ここで読む-セットで）ノード、つまり各頂点X-一つは真でなければなりません-「{」の左に1つ-右に1つ「}」アトムは色（X、C）であり、Cは色のセット（単項述語色/ 1）から私たちのところに来ました。

ASPの主な機能の1つは、制約がソリューションではないものを定義することです。たとえば、次のルールを考慮してください。

 :- edge(X,Y), color(X,Cx), color(Y,Cy), Cx = Cy. 

制約（用語： 整合性制約は英語の科学文献で使用されます ）-実際、ルールは記事の最初からのものです-それらは「空の頭」〜空の頭のみを持ちます。実際、これは次の形式のルールの略語です：

 false :- a_1, a_2, … a_n 

つまり a_1、... a_nが実行されると、「false」が出力され、これはモデルではありません。
（より正確には：falseはbの構文です：-bではなくa_1、.... a_n-bはfalseであるという仮定の下で出力されます-これは矛盾です）。

これは理論上の余談を終わらせ、ルールを詳しく見ていきます-XとYの間に弧があり、色XがCxで、色YがCyでCx == Cyである場合、これは解ではありません。

ちなみに、ASPに精通している人はこのルールを次のように書くでしょう。

 :- edge(X,Y), color(X,C), color(Y,C). 

同じルール内で同じ名前の変数は等しいと見なされます（そして、これは基本的な段階で役立つ可能性が高いですが、これは別の話です）。

私たちは、全体としての（そしてさらにいくつかの）問題全体の説明に目を向けます。

一般的な組み合わせの問題をいくつか分析します：NP完全

ここで説明するコードは、 クラスプで実行するのが最適です（アートワークとコメントを書く前にテストしました）。

次のタスクについて説明します。

• グラフの色付け ： グラフが指定されている場合、2つの頂点が同じ色でペイントされないように、3色で色付けできるかどうかを判断する必要があります。
• 黒と白の女王 ：ボード上でnからnまで、k個の黒と白の女王を配置します。したがって、異なる色の2人の女王が互いに勝つことはありません。

そして、ASPを使用してそれらのそれぞれを解決し、同時に主要なモデリング手法を分析します。

カウントカラーリング

ダンカウント：

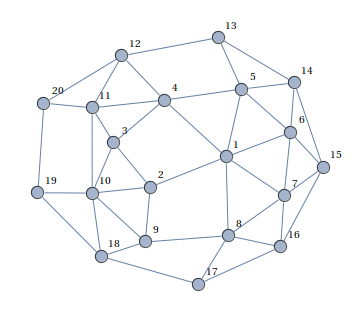
2つの隣接する頂点が同じ色にならないように、またはこれが不可能であると言うために、頂点を3色（赤青緑）で着色する必要があります。

出力：

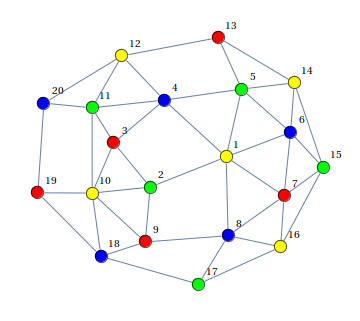
（ ここから撮影した写真）

ASPコードの主な構成については既に検討しました-残りの要素を見ていきます：node / 1（node（a）。Node（b）...）-グラフの多くの頂点を宣言します。順序は重要ではありません。edge/ 2-弧を宣言します。 ASP（および論理プログラミング）のこのようなアトムは-事実、実際には「a：-true」の略語です。しかし、常に真であるステートメントから導き出されます。つまり、アトムはプログラムデータを指定します。

 % --  ,          "%" %     node(a). node(b). node(c). node(d). %    edge(a,b). edge(a,d). edge(b,c). edge(b,d). edge(c,d). % ,    X  Y,  ,    Y  X   --    edge(Y,X) :- edge(X,Y). %    colors(red). colors(green). colors(blue). % ,    ,             colors(.)  1 { color(X,C) : colors(C) } 1 :- node(X). %    X, Y (- )      ,  Cx = Cy,     :- edge(X,Y), color(X,C), color(Y,C). %       #show color/2. 

黒と白の女王

クイーンの配置について（このバリエーションを含めます）、 ここで詳細に説明しました 。

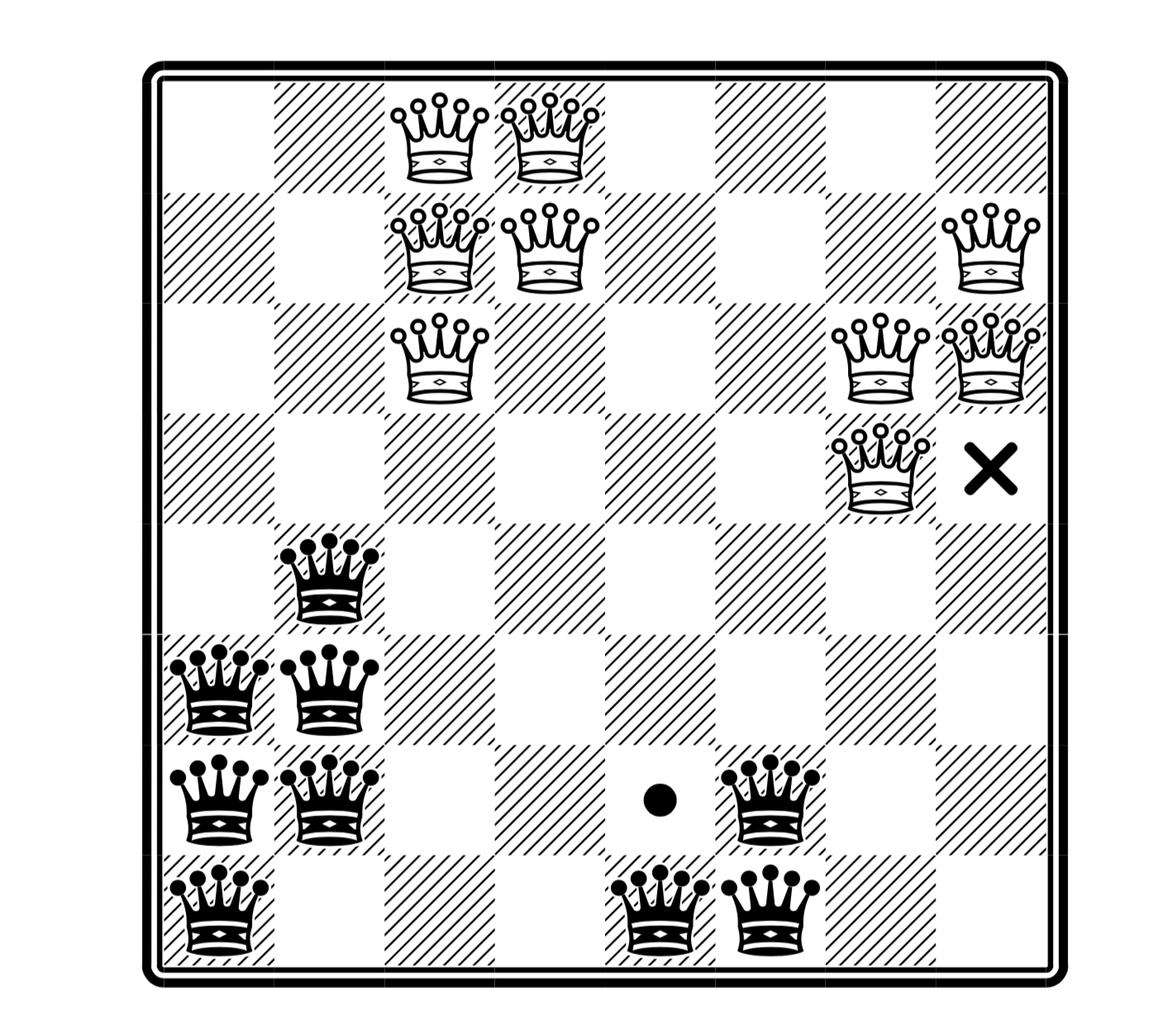
（ここではクイーンの最大数、そして十字架の代わりに白を、黒点の代わりに置くことができます-同時に両方ではありません; 記事から取られました）

ここで与えられたコードは、クイーンの配列の単純な多項式バージョンとNPフルバージョンの両方を解決します（クイーンに関するHabraの記事を参照してください。ここでは、古典バージョンの複雑さの結果もこのバリエーションに適用されると仮定します）。

 %       "k"    "m" #const k=2. #const m=4. %      color(b). color(w). col(1..m). row(1..m). %       k ,       k { queen(C,Row,Col) : col(Col), row(Row) } k :- color(C). %      Rw -- row white, Cb -- column black, etc %           :- queen(w,Rw,Cw), queen(b,Rb,Cb), Rw = Rb. %           :- queen(w,Rw,Cw), queen(b,Rb,Cb), Cw = Cb. %           :- queen(w,Rw,Cw), queen(b,Rb,Cb), | Rw - Rb | = | Cw - Cb |. 

コードをより詳細に分析してみましょう。次のルールはボードパラメータを設定します。実際、クイーンの多くの色で問題を解決できます。ここでの色は述語値color/1形式で記述されます。

 %       "k"    "m" #const k=2. #const m=4. %      color(b). color(w). col(1..m). row(1..m). 

次に、サーチスペースを宣言する必要があります。

 %       k ,       k { queen(C,Row,Col) : col(Col), row(Row) } k :- color(C). 

実際、このルールは次のように読み取られます。各色Cに対して、色Cの k個と正確にk個のクイーンが必要であり、 RowおよびColの値は述語col/1およびrow/1のセットからのものでなければなりません。 簡単に言えば、各色について、正しい（ボード上の）クイーンの数をkに設定します。

次に、解決策ではないものについて説明します。同じ行、列、または対角線上に異なる色がある場合：

 %           :- queen(w,Rw,Cw), queen(b,Rb,Cb), Rw = Rb. %           :- queen(w,Rw,Cw), queen(b,Rb,Cb), Cw = Cb. %           :- queen(w,Rw,Cw), queen(b,Rb,Cb), | Rw - Rb | = | Cw - Cb |. 

実際、コードは2つの部分にうまく分解されていることがわかります。検索スペース（推測）+回答の検証（チェック）-ASPでは、これは推測とチェックのパラダイムと呼ばれ、すべてのコードは方程式Problem = Data + Model -SATとは異なり、データを変更しても、新しいクイーンを追加しても、制限自体（モデルルール）は変わりません。 一般に、これらのルールを書き換えて、色をパラメータとして受け入れることもできます。

組み合わせ最適化について簡単に

一番下の行は単純です： ハミルトンサイクル （NP完全問題）を見つけるなどの組み合わせタスクがありますが、追加の条件があります：最小化する必要があるもの-たとえば、パスの重み（グラフを着色する色の数、女王の数または女王の色を最大化するなど）。 ）原則として、これによりタスクの複雑さが急増し、検索がかなり複雑になります。 ASPには、組み合わせ最適化問題を解決するための標準メカニズムがあります。

パスの重みを最適化してハミルトンサイクルを見つける問題を分析しましょう（Answer Set Solving in Practiceのコード。MartinGebser et al。;私のコメント）

 % === GUESS === %    --         1 { cycle(X,Y) : edge(X,Y) } 1 :- node(X). %    1 { cycle(X,Y) : edge(X,Y) } 1 :- node(Y). %    1 % === AUXILIARY INFERENCE === reached(Y) :- cycle(1,Y). %     reached(Y) :- cycle(X,Y), reached(X). % === CHECK === %  -       --    :- node(Y), not reached(Y). % === MINIMIZE === %   --   ,         #minimize [ cycle(X,Y) = C : cost(X,Y,C) ]. 

, ASP :

Problem Model = Guess + Check + Minimize

(auxiliary inference), . , ASP.

Prolog — ProbLog

Prolog , — , — ProbLog ( , — , ) — Probabilistic Prolog.

A Statistical Learning Method for Logic Programs with Distribution Semantics by Taisuke Sato

(, , — ILP 2015 — )

( - tutorial, )

, , , , , , , 0.5, 0.6 — , ?

 % Probabilistic facs: 0.6::heads(C) :- coin(C). % Background information: coin(c1). coin(c2). coin(c3). coin(c4). % Rules: someHeads :- heads(_). % Queries: query(someHeads). 

— , ( — ), — someHeads — , — . — : .

ProbLog — , ( ) .

FO(.) IDP

FO(.) IDP — Answer Set Programming: FO(.) — First Order (.) — , . IDP — , FO(.). ( — FO(.) IDP PhD , - ).

, . IDP .

 /********************************* A Sudoku solver in IDP *********************************/ vocabulary V { type row isa int // The rows of the grid (1 to 9) type column isa int // The columns of the grid (1 to 9) type number isa int // The numbers of the grid (1 to 9) type block isa int // The 9 blocks of 3x3 where the numbers need to be entered liesInBlock(row, column, block) //This declares which cells belongs to which blocks. //This means that liesInBlock(r, k, b) is true if and only if // the cell on row r and column c lies in block b. solution(row, column) : number //The solution: every cell has a number //A cell is represented by its row and column. //For example: solution(4,5) = 9 means that the cell on row 4 and column 5 contains a 9. } theory T : V { //On every row every number is present. ! r : ! n : ? c : solution(r,c) = n. //In every column every number is present. ! c : ! n : ? r : solution(r,c) = n. //In every block every number is present. ! b : ! n : ? rc : liesInBlock(r,c,b) & solution(r,c) = n. //Define which cells lie in which block { liesInBlock(r,k,b) <- b = (((r - 1) - (r - 1)%3) / 3) * 3 + (((k - 1)-(k - 1)%3) / 3) + 1. } } 

, . : . — solution(row, column) -> {1,...,9}, :

, , (r, c) n . .

→

→

Sketched Answer Set Programming

— ( , , ). , (logic programming) (machine learning), Inductive Logic Programming . , ASP.

Sketched Answer Set Programming by Sergey Paramonov, Christian Bessiere, Anton Dries, Luc De Raedt

, ASP — Constraint Programming Essense .

-- ASP, :

 :- queen(w,Rw,Cw), queen(b,Rb,Cb), Rw != Rb. :- queen(w,Rw,Cw), queen(b,Rb,Cb), Cw != Cb. :- queen(w,Rw,Cw), queen(b,Rb,Cb), |Rw - Rb| != |Cw - Cb|. 

Unsatisfiable . sketching , " , " , — " , "

 [Sketch] :- queen(w,Rw,Cw), queen(b,Rb,Cb), Rw ?= Rb. :- queen(w,Rw,Cw), queen(b,Rb,Cb), Cw ?= Cb. :- queen(w,Rw,Cw), queen(b,Rb,Cb), Rw ?+ Rb ?= Cw ?+ Cb. [Examples] positive: queen(w,1,1). queen(w,2,2). queen(b,3,4). queen(b,4,3). negative: queen(w,1,1). queen(w,2,2). queen(b,3,4). queen(b,4,4). 

, , , , , . ( ).

sketching — .

ASP — , , — NP- N-queens — .

, , .

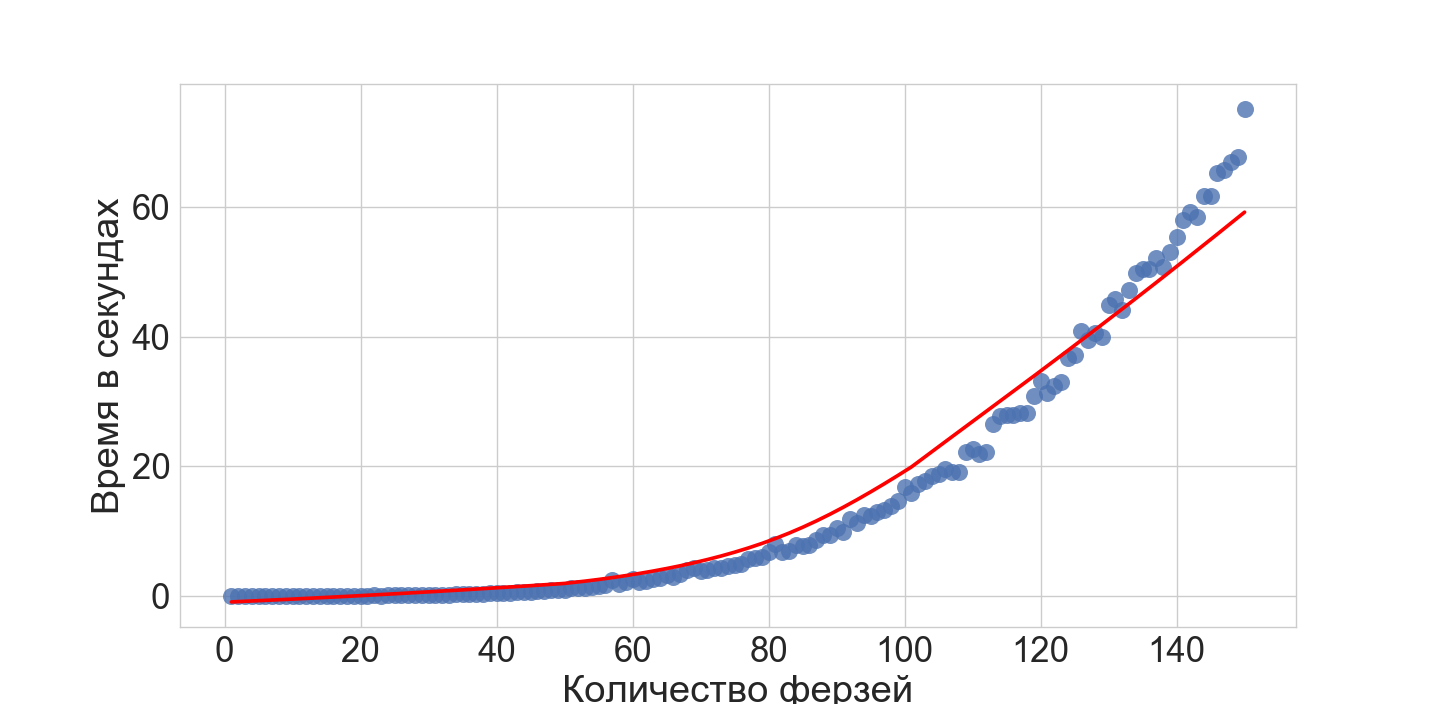
vs

Relational Data Factorization (Paramonov, Sergey; van Leeuwen, Matthijs; De Raedt, Luc: Relational data factorization, Machine Learning, volume 106) , :

— ( + ~= ) — — , ASP — .

: + , :

= + ASP

, structured frequent pattern mining (. Paramonov, Sergey; Stepanova, Daria; Miettinen, Pauli: Hybrid ASP-based Approach to Pattern Mining, Theory and Practice of Logic Programming, 2018 ):

( ; — -, )

, ( )

, , .

, , , . :

, , , , LCM-k:

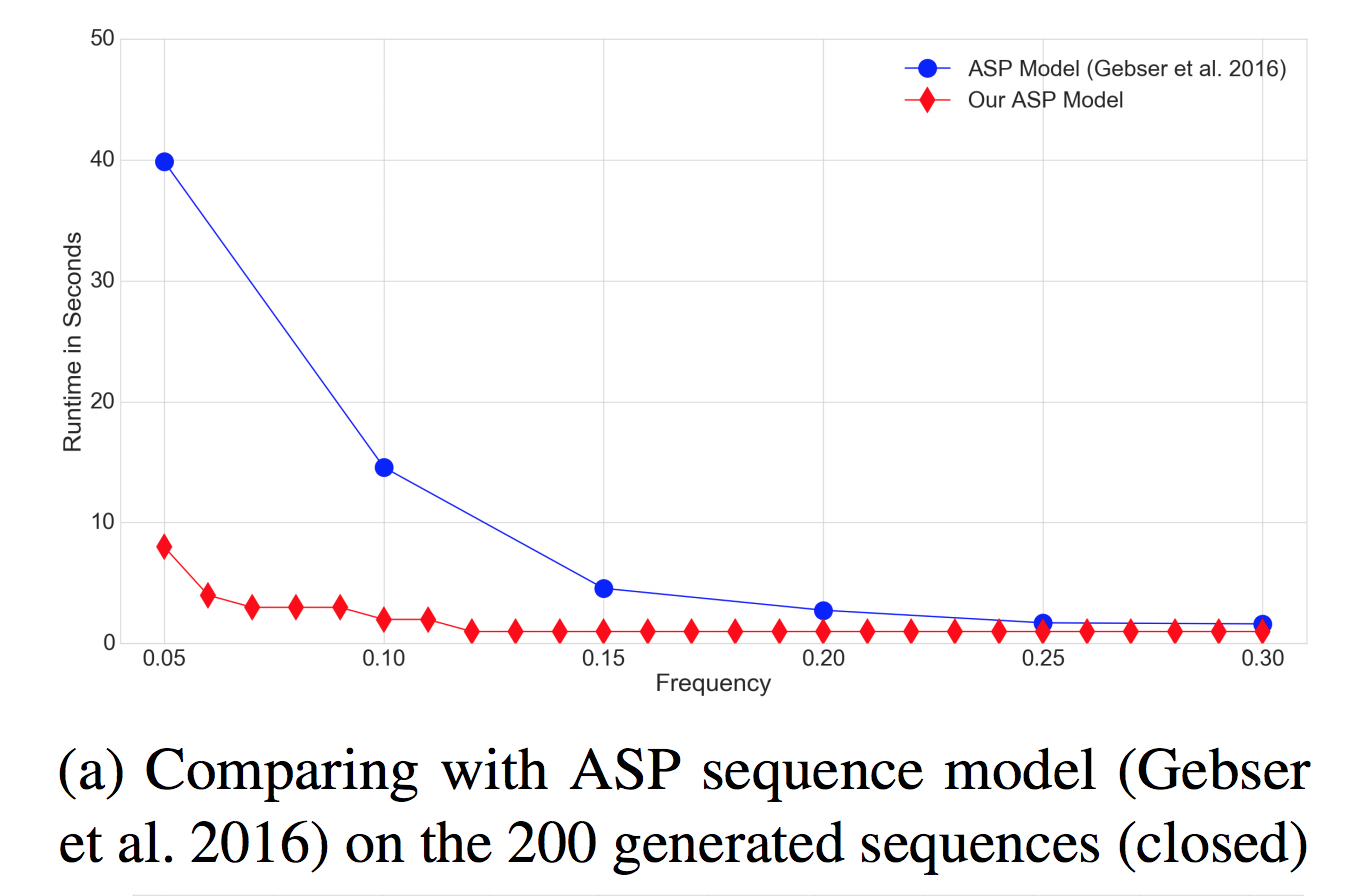
LCM-k

, , "ASP solver", .. Answer Set Programming. , — . , , — . , , ASP .

, ( ), "?" :

ASP — algorithm implementation ( ASP ), .

, :

• baseline

おわりに

() — . (tl;dr) :

• != ;
• ASP ;
• : + ;
• ASP : " - ?", " ?", etc;
• , , ASP .