以前(
1、2 )、存在の可能性を実証し、実証しました
通常のBツリーのすべての利点を備えた空間インデックス-インデックスと
R-Treeに基づくインデックスよりもパフォーマンスが劣っていません。
カットの下で、アルゴリズムの3次元空間への一般化、最適化、ベンチマーク。
3D
なぜこの3Dが必要なのですか? 実際、私たちは三次元の世界に住んでいます。 したがって、データは地理座標(緯度、経度)で表示され、赤道から離れるほど歪みが大きくなります。 または、これらの座標の特定の空間でのみ適切な投影がそれらに添付されます。 3次元インデックスを使用すると、球体にポイントを配置して、大幅な歪みを回避できます。 検索範囲を取得するには、球上の目的の立方体の中心を特定し、すべての座標で半径によって側面に後退するだけで十分です。
アルゴリズムの基本的に3次元のバージョンは2次元のアルゴリズムと違いはありません-唯一の違いはキーを操作することです:
- キーの数字の交替は、2ではなく3の増分になりました。 ... z1y1x1z0y0x0
- キーは64ビットではなく96になりました。 64ビットキーにすべてを配置するオプションは拒否されます。 座標ごとに合計21ビットが与えられるため、少し制約があります。 さらに、4次元キーと6次元キーが登場し(理由を推測)、64で十分ではないので、なぜ避けられないのを遅らせます。 幸いなことに、それほど難しくはありません
- したがって、キーはもはやbigintではなく、数値であり、キーインターフェースは数値からの変換メソッドを必要とし、その逆も同様です
- 座標からキーを取得して戻すメソッドは変更されます
- 同様に、サブクエリ分割メソッド。 左下隅と右上隅に対応する2つのキーで表されるクエリを分割することを思い出してください。
- それらの中で最も古い異なるビットmを見つけました
- 小さい新しいサブクエリの右上隅は、mより小さい対応するm座標のすべてのビットを1に設定することによって取得されます
- 大きい新しいサブクエリの左下隅は、mより小さい対応するm座標のすべてのビットを0に設定することにより取得されます
実際には、何も変わっていません。ある座標のビットだけが別のステップに進みます
数値
数値自体は、拡張機能から直接アクセスできません。 マーシャリングで関数を呼び出すための汎用メカニズムを使用する必要があります-'include / fmgr.h'からのDirectFunctionCall [X]。Xは引数の数です。
内部では、数値は短い配列として配置され、各配列には4桁の10進数が含まれます-0から9999まで。インターフェースにモジュールを返すシフトや除算はありません。 度2で作業するための特別な機能(このようなデバイスでは、それらは場違いです)。 したがって、数値を2つのint64に解析するには、次のように動作する必要があります。
void bit3Key_fromLong(bitKey_t *pk, Datum dt) { Datum divisor_numeric; Datum divisor_int64; Datum low_result; Datum upper_result; divisor_int64 = Int64GetDatum((int64) (1ULL << 48)); divisor_numeric = DirectFunctionCall1(int8_numeric, divisor_int64); low_result = DirectFunctionCall2(numeric_mod, dt, divisor_numeric); upper_result = DirectFunctionCall2(numeric_div_trunc, dt, divisor_numeric); pk->vals_[0] = DatumGetInt64(DirectFunctionCall1(numeric_int8, low_result)); pk->vals_[1] = DatumGetInt64(DirectFunctionCall1(numeric_int8, upper_result)); pk->vals_[0] |= (pk->vals_[1] & 0xffff) << 48; pk->vals_[1] >>= 16; }
そして、逆変換の場合-このように:
Datum bit3Key_toLong(const bitKey_t *pk) { uint64 lo = pk->vals_[0] & 0xffffffffffff; uint64 hi = (pk->vals_[0] >> 48) | (pk->vals_[1] << 16); uint64 mul = 1ULL << 48; Datum low_result = DirectFunctionCall1(int8_numeric, Int64GetDatum(lo)); Datum upper_result = DirectFunctionCall1(int8_numeric, Int64GetDatum(hi)); Datum mul_result = DirectFunctionCall1(int8_numeric, Int64GetDatum(mul)); Datum nm = DirectFunctionCall2(numeric_mul, mul_result, upper_result); return DirectFunctionCall2(numeric_add, nm, low_result); }
一般に、任意の精度の算術を使用することは、特に除算に関しては高速ではありません。 したがって、作者は、数値を「ハッキング」し、自分で数値を分解するという非常に魅力的な欲求を持っていました。 私は、numeric.cからローカル定義を複製し、生のショートを処理する必要がありました。 それは簡単で、作業を10倍に加速しました。
継続的なサブクエリ。
思い出したように、アルゴリズムはサブクエリを分割し、その下のデータが1つのディスクページに完全に収まるようにします。 次のようになります
- 入力、サブクエリでは、左下(近く)と右上(遠)の間に値の間隔があります。 より多くの座標がありますが、本質は同じです
- より小さな角度キーのBTree検索を行います
- シートページに行き、最後の値を確認します
- 最後の値> =より大きな角度のキー値の場合、ページ全体を見て、検索範囲に入るすべてのものを出力に入れます
- 少ない場合は、リクエストの分割を続けます
ただし、データが数十または数百ページに含まれるサブクエリが、元の検索範囲内に完全に配置される場合があります。 それをさらにカットするポイントはありません。間隔からのデータは、チェックなしで結果に安全に入力できます。
そのようなサブクエリを認識する方法は? とてもシンプル-
- すべての座標での次元は2度以上でなければなりません(立方体)
- 角度は、同じ次数2の増分で対応する格子上になければなりません
これは、キューブを使用した最適化前のサブクエリマップの外観です。

そしてその後:
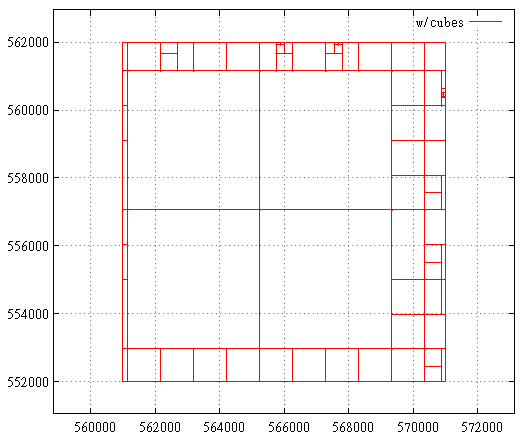
ベンチマーク
この表は、元のアルゴリズム、最適化されたバージョン、およびGiST Rツリーの比較結果をまとめたものです。
Rツリーは2次元です;比較のために、擬似3Dデータがz-indexに入力されました。 (x、0、z)。 アルゴリズムの観点からは違いはありません。Rツリーに有利なスタートを切るだけです。
データ-[0 ... 1 000 000、0 ... 0、0 ... 1 000 000]の100 000 000ランダムポイント。
測定は2つのコアと4 GBのRAMを備えた控えめな仮想マシンで実行されたため、時間に絶対値はありませんが、読み取られたページ数は信頼できます。
ホットサーバーと仮想マシンでの2回目の実行で時間が表示されます。 読み取られたバッファーの数は、新しく生成されたサーバー上にあります。
| Nポイント | Nreq | 種類 | 時間(ミリ秒) | 読みます | ヒット数 |
|---|
| 1 | 100,000 | 古い
新しい
rtree | .37
.36
.38 | 1.13154
1.13307
1.83092 | 3.90815
3.89143
3.84164 |
| 10 | 100,000 | 古い
新しい
rtree | .40
.38
.46 | 1.55
1.57692
2.73515 | 8.26421
7.96261
4.35017 |
| 100 | 100,000 | 古い
新しい
rtree(*) | .63
.48
.50 ... 7.1 | 3.16749
3.30305
6.2594 | 45.598
31.0239
4.9118 |
| 1,000 | 100,000 | 古い
新しい
rtree(*) | 2.7
1.2
1.1 ... 16 | 11.0775
13.0646
24.38 | 381.854
165.853
7.89025 |
| 10,000 | 10,000 | 古い
新しい
rtree(*) | 22.3
5.5
4.2 ... 135 | 59.1605
65.1069
150.579 | 3606.73
651.405
27.2181 |
| 100,000 | 10,000 | 古い
新しい
rtree(*) | 199
53.3
35 ... 1200 | 430.012
442.628
1243.64 | 34835.1
2198.11
186.457 |
| 1,000,000 | 1,000 | 古い
新しい
rtree(*) | 2550
390
300 ... 10000 | 3523.11
3629.49
11394 | 322776
6792.26
3175.36 |
どこで
Npoints-出力の平均ポイント数
Nreq-シリーズ内のクエリの数
タイプ -「古い」-元のバージョン、
'new'-数値最適化と連続サブクエリを使用。
'rtree'-2D rtreeのみを要点、
(*)-検索時間を比較するために、
シリーズを10倍減らす必要がありましたが、
そうでない場合、ページはキャッシュに収まりませんでした
時間(ミリ秒) -平均クエリ実行時間
読み取り -要求ごとの読み取りの平均数
ヒット -バッファアクセスの数
グラフの形式では、これらのデータは次のようになります。
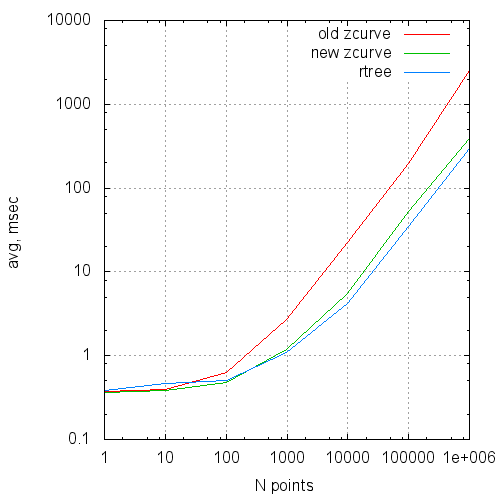
平均クエリ実行時間とリクエストサイズ

リクエストあたりの平均読み取り数とリクエストサイズ
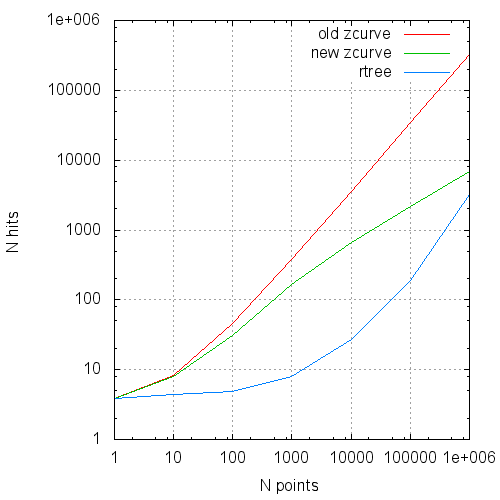
リクエストあたりの平均ページキャッシュヒット対リクエストサイズ
結論
これまでのところ良い。 空間インデックス作成にヒルベルト曲線を使用すること、および非合成データの本格的な測定に向けて引き続き取り組みます。
PS:説明された変更は
ここにあり
ます 。