
コースの5番目の記事は、バギングとランダムフォレストの単純な構成方法に専念します。 ほんの一部の情報しか持っていない場合、一般母集団の平均の分布を取得する方法を学習します。 アルゴリズムの構成を使用して分散を削減し、モデルの精度を向上させる方法を見てみましょう。 ランダムフォレストとは何か、「ツイスト」する必要があるパラメータ、および最も重要な兆候を見つける方法を分析します。 数学の「ピンチ」を追加することにより、練習に焦点を当てます。
UPD:現在、コースは英語で、 mlcourse.aiというブランド名で、Medium に関する記事 、Kaggle( Dataset )およびGitHubに関する資料があります 。
オープンコースの2回目の立ち上げ(2017年9月から11月)の一環として、この記事に基づいた講義のビデオ 。
この記事の概要
- バギング
- ランダムフォレスト
- 症状の重要性の評価
- ランダムフォレストの長所と短所
- 宿題№5
- 有用なソース
1.バギング
過去の講義から、さまざまな分類アルゴリズムについて学習し、モデルの品質を正しく検証および評価することも学習しました。 しかし、すでに最良のモデルを見つけていて、モデルの精度をそれ以上改善できない場合はどうでしょうか? この場合、より高度な機械学習手法を適用する必要があります。これは「アンサンブル」という言葉と組み合わせることができます。 アンサンブルは特定の集合体であり、その一部は単一の全体を形成します。 日常生活から、いくつかの楽器が組み合わされた音楽アンサンブル、異なる建物の建築アンサンブルなどを知っています。
アンサンブル
アンサンブルの良い例は、コンドルセのju審定理(1784)です。 ジュリーの各メンバーが独立した意見を持ち、ジュリーの正しい決定の確率が0.5を超える場合、ジュリー全体の正しい決定の確率は、ジュリーのメンバーの数とともに増加し、団結する傾向があります。 ジュリーの各メンバーに適切である確率が0.5未満の場合、ジュリーが全体として正しい決定を下す確率は単調に減少し、審査員の数が増えるとゼロになる傾向があります。
\大N -ju審員数
\大p -正しい審査員の決定の確率
\大 mu -審査員全員による正しい決定の確率
\大m -minimum審員の最小過半数、 m= textfloor(N/2)+1
\大CiN -の組み合わせの数 N によって i
large mu= sumNi=mCiNpi(1−p)N−i
もし \大p>0.5 それから large mu>p
もし \大N\右矢印 infty それから \大 mu\右矢印1
アンサンブルの別の例を見てみましょう-「群衆の知恵」。 フランシス・ガルトンは1906年に市場を訪れ、そこで農民の宝くじが開催されました。 
約800人が集まり、彼らは彼らの前に立っていた雄牛の体重を推測しようとしました。 雄牛の体重は1,198ポンドでした。 雄牛の正確な体重を推測した農民は一人もいませんが、予測の平均を計算すると、1,197ポンドが得られます。
このエラー削減の考え方は、機械学習に適用されています。
ブートストラップ
バギング(ブートストラップアグリゲーションから)は、アンサンブルの最初で最も簡単なタイプの1つです。 1994年にLeo Breimanによって造られました。 バギングは、ブートストラップ統計法に基づいており、複雑な分布の多くの統計を評価できます。
ブートストラップ方法は次のとおりです。 選択してみましょう \大X サイズ \大N 。 サンプルから均等に取る \大N 戻り値を持つオブジェクト。 これはつまり、 \大N 任意のサンプルオブジェクトを選択する回数(各オブジェクトは同じ確率で「取得」すると考えられます) \大 frac1N )、およびすべてのソースから選択するたびに \大N オブジェクト。 ボールが取り出されるバッグを想像できます。あるステップで選択されたボールがバッグに戻され、同じ数のボールから次の選択が再び同様に行われます。 復帰のため、繰り返しがそれらの中にあることに注意してください。 新しい選択を示す \大X1 。 手順を繰り返す \大M 回、生成 \大M サブサンプル \大X1、\ドット、XM 。 現在、かなり多数のサンプルがあり、初期分布のさまざまな統計を評価できます。
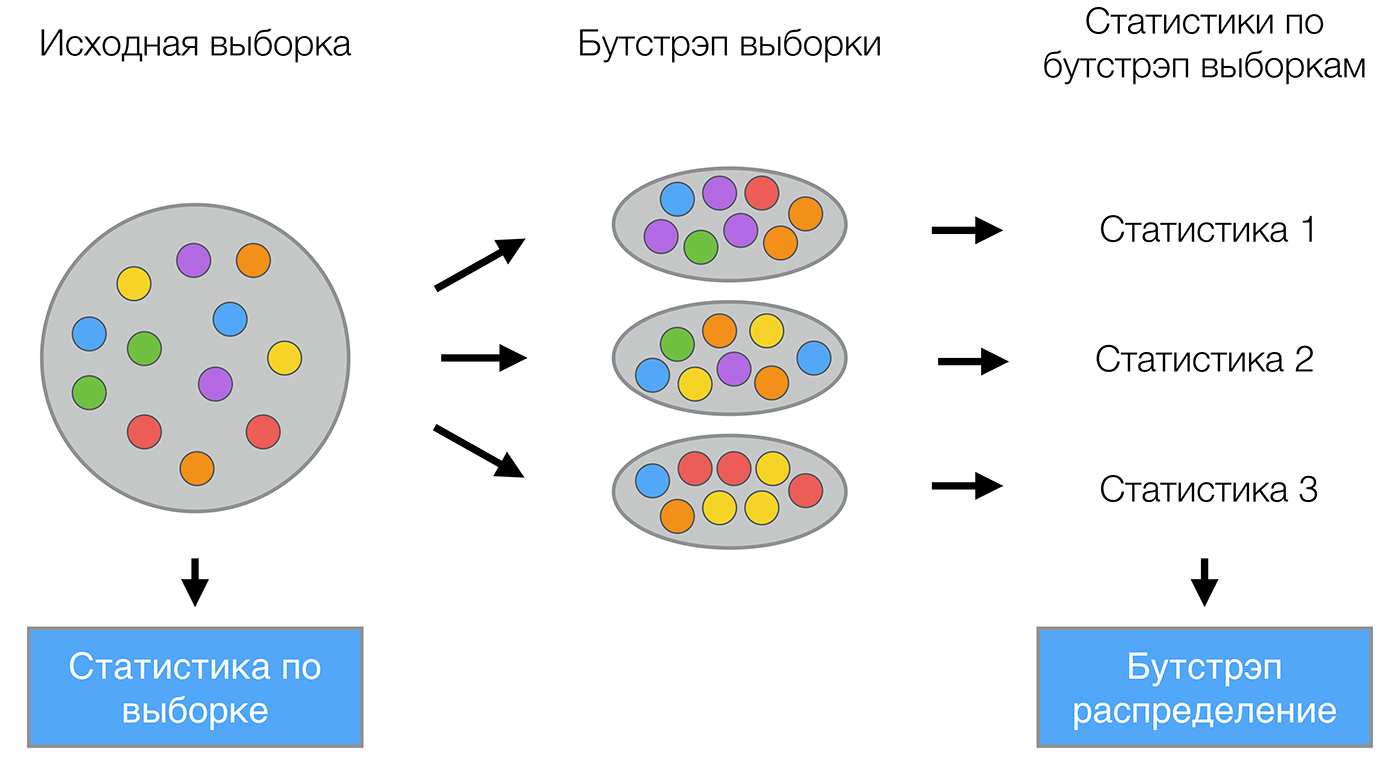
たとえば、既に知っているコースの過去のレッスンのtelecom_churnを見てみましょう。 これは顧客チャーンのバイナリ分類タスクであることを思い出してください。 このデータセットで最も重要な兆候の1つは、クライアントによって行われたサービスセンターへの呼び出しの数です。 データを視覚化し、この特性の分布を見てみましょう。
データを読み込んでプロットするためのコード import pandas as pd from matplotlib import pyplot as plt plt.style.use('ggplot') plt.rcParams['figure.figsize'] = 10, 6 import seaborn as sns %matplotlib inline telecom_data = pd.read_csv('data/telecom_churn.csv') fig = sns.kdeplot(telecom_data[telecom_data['Churn'] == False]['Customer service calls'], label = 'Loyal') fig = sns.kdeplot(telecom_data[telecom_data['Churn'] == True]['Customer service calls'], label = 'Churn') fig.set(xlabel=' ', ylabel='') plt.show()

お気づきかもしれませんが、忠実な顧客向けのサービスセンターへの電話の回数は、以前の顧客よりも少なくなっています。 ここで、各グループが平均して何回の呼び出しを行うかを推定するとよいでしょう。 データセットにはデータがほとんどないので、平均値を探すのは適切ではありません。ブートストラップの新しい知識を適用することをお勧めします。 母集団から1,000個の新しいサブサンプルを生成し、平均の区間推定を行いましょう。
ブートストラップを使用して信頼区間を構築するためのコード import numpy as np def get_bootstrap_samples(data, n_samples):
その結果、95%の確率で、忠実な顧客からのコールの平均数は1.40から1.50の間であり、以前の顧客からのコールは平均で2.06から2.40回であることがわかりました。 また、忠実な顧客の間隔は狭く、これは非常に論理的であり、頻繁に電話をかけることはほとんどなく(主に0、1、または2回)、不満のある顧客はより頻繁に電話をかけますが、時間の経過とともに忍耐が終了するという事実に注意することもできます演算子を変更します。
バギング
これでブーストのアイデアが得られました。直接バギングに進むことができます。 トレーニングサンプルを用意します。 \大X 。 ブートストラップを使用して、そこからサンプルを生成します \大X1、\ドット、XM 。 各サンプルで分類器を訓練します \大ai(x) 。 最終分類子は、これらすべてのアルゴリズムの応答を平均化します(分類の場合、これは投票に対応します)。 largea(x)= frac1M sumMi=1ai(x) 。 このスキームは、次の図で表すことができます。
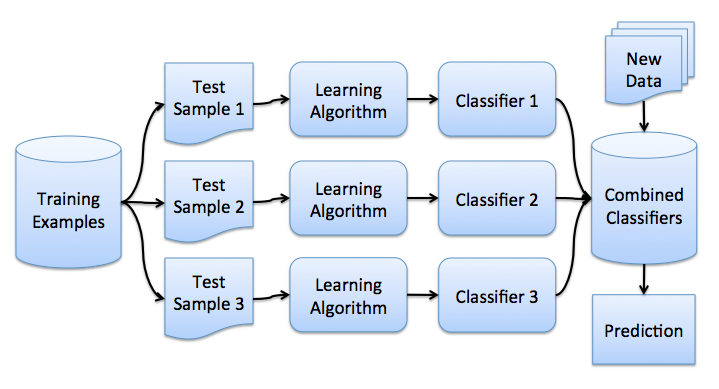
基本的なアルゴリズムを使用した回帰問題を検討する \大b1(x)、\ドット、bn(x) 。 すべてのオブジェクトに対して真の応答関数があると仮定します \大y(x) 、またオブジェクト上の分布が設定されます \大p(x) 。 この場合、各回帰関数のエラーを記録できます
\大 varepsiloni(x)=bi(x)−y(x)、i=1、\ドット、n
平均二乗誤差を書きます
\大きいEx(bi(x)−y(x))2=Ex varepsilon2i(x)。
構築された回帰関数の平均誤差の形式は
largeE1= frac1nEx sumni=1 varepsilon2i(x)
エラーが公平で無相関であると仮定します。
large beginarrayrclEx varepsiloni(x)&=&0、Ex varepsiloni(x) varepsilonj(x)&=&0、i neqj。 endarray
次に、構築した関数の応答を平均する新しい回帰関数を作成します。
largea(x)= frac1n sumni=1bi(x)
その二乗平均平方根誤差を見つけます。
large beginarrayrclEn&=&Ex Big( frac1n sumni=1bi(x)−y(x) Big)2&=&Ex Big( frac1n sumni=1 varepsiloni Big)2&=& frac1n2Ex Big( sumni=1 varepsilon2i(x)+ sumi neqj varepsiloni(x) varepsilonj(x) Big)&=& frac1nE1 endarray
したがって、回答を平均化することで、エラーの平均二乗をn倍減らすことができました!
以前のレッスンで 、一般的なエラーがどのようにレイアウトされているかを思い出してみましょう。
large beginarrayrcl textErr left( vecx right)&=& mathbbE left[ left(y− hatf left( vecx right) right)2 right]&=& sigma2+f2+ textVar left( hatf right)+ mathbbE\左[ hatf\右]2−2f mathbbE\左[ hatf\右]&=&\左(f− mathbbE left[ hatf right] right)2+ textVar left( hatf right)+ sigma2&=& textBias left( hatf right)2+ textVar left( hatf right)+ sigma2 endarray
バギングを使用すると、トレーニング済みの分類器の分散を減らすことができ、異なるデータセットでモデルをトレーニングする場合、つまり再トレーニングを防ぐ場合にエラーがどれだけ異なるかによって量を減らすことができます。 バギングの有効性は、さまざまなサブサンプルでトレーニングされた基本アルゴリズムがまったく異なり、投票によってエラーが相互に補正されるという事実と、外れ値オブジェクトがいくつかのトレーニングサブサンプルに分類されない可能性があるという事実により達成されます。
scikit-learnライブラリには、他のほとんどのアルゴリズムを「内部」で使用できるBaggingRegressorおよびBaggingClassifier実装があります。 バギングがどのように機能するかを実際に調べ、 ドキュメントの例を使用して決定ツリーと比較してみましょう。

デシジョンツリーエラー
\大0.0255(Err)=0.0003(バイアス2)+0.0152(Var)+0.0098( sigma2)
バギングエラー
\大0.0196(Err)=0.0004(バイアス2)+0.0092(Var)+0.0098( sigma2)
上記のグラフと結果は、上で理論的に証明したように、バギングを使用すると分散誤差がはるかに小さくなることを示しています。
トレーニングオブジェクトのごく一部を除外しても、大幅に異なる基本分類子が作成される場合、バギングは小さなサンプルに対して効果的です。 大きいサンプルの場合、通常、かなり短い長さのサブサンプルが生成されます。
相関関係のないエラーを想定しているため、この例は実際にはあまり適用されないことに注意してください。 この仮定が正しくない場合、エラーの減少はそれほど重要ではありません。 次の講義では、現実世界の問題で高品質を達成できるアルゴリズムを組み合わせて合成するより複雑な方法を検討します。
アウトオブバッグエラー
今後、ランダムフォレストを使用する場合、テストスイートエラーの公平な推定値を取得するために、相互検証または個別のテストスイートは必要ないことに注意してください。 トレーニング中にモデルの「内部」評価がどのように取得されるかを見てみましょう。
各ツリーは、ソースデータからの異なるブートストラップサンプルを使用して構築されます。 例の約37%はブートストラップサンプルの外に残り、k番目のツリーの構築には使用されません。
これは簡単に証明できます:サンプルに入れましょう \大\エル オブジェクト。 各ステップで、すべてのオブジェクトが同じ確率で返されるサブサンプルに分類されます。つまり、確率を持つ個別のオブジェクトです。 large frac1 ell。 オブジェクトがサブサンプルに分類されない可能性(つまり、取得されなかった \大\エル 回): large(1− frac1 ell) ell 。 で \大 ell\右矢印+ infty 「素晴らしい」制限の1つを取得します \大 frac1e 。 次に、特定のオブジェクトがサブサンプルに陥る確率 \大\約1− frac1e\約63\% 。
これが実際にどのように機能するかを見てみましょう。
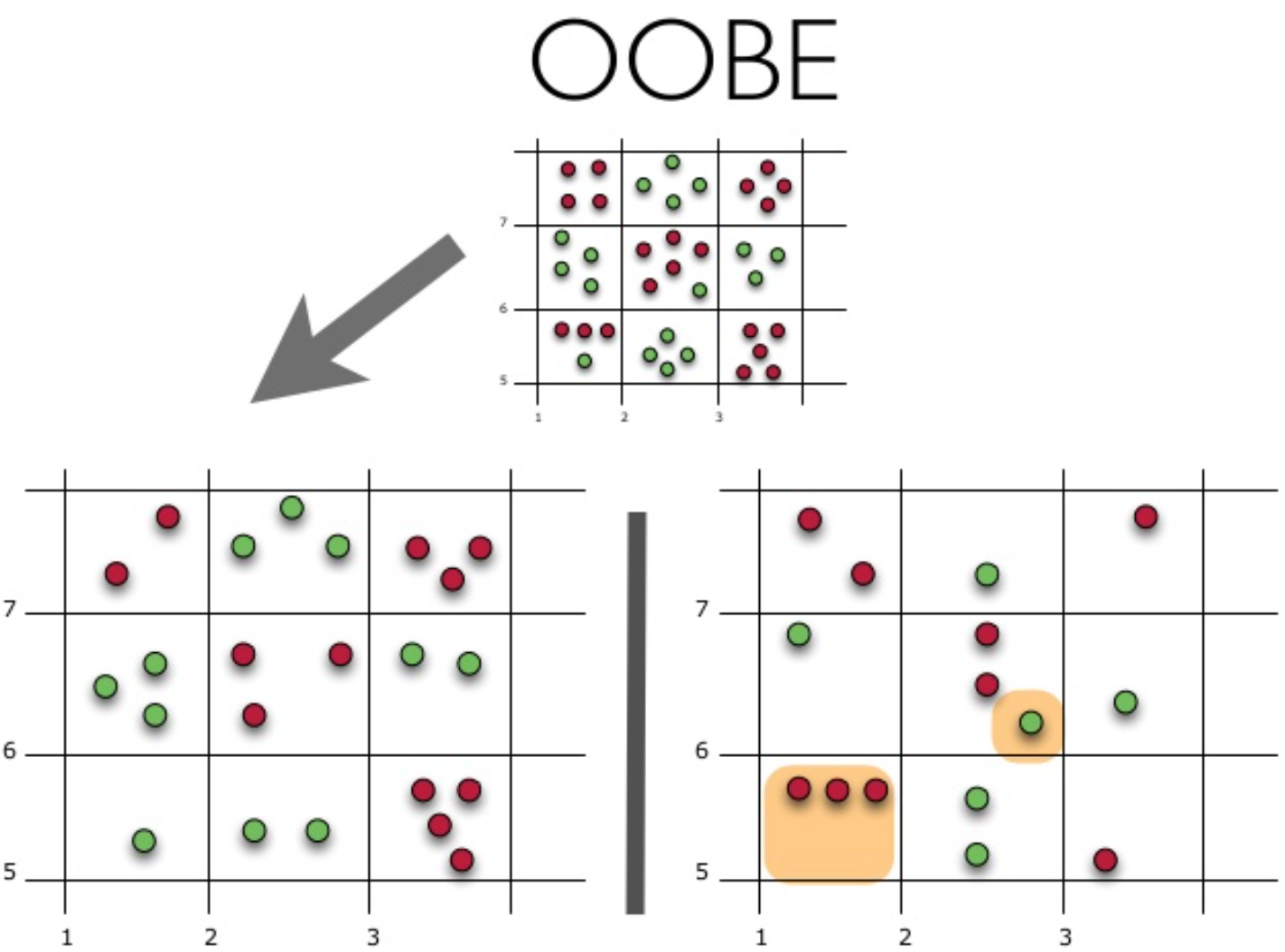
この図は、oobエラーの推定値を示しています。 上の図は最初のサンプルです。トレーニング(左側)とテスト(右側)に分けます。 左の図では、サンプルを完全に分割する正方形のグリッドがあります。 次に、テストサンプルで正解の割合を推定する必要があります。 この図は、トレーニングに使用しなかった4つの観測で分類器が誤っていたことを示しています。 したがって、分類器の正解のシェア: large frac1115∗100\%=73.33\%
各基本アルゴリズムは、元のオブジェクトの〜63%でトレーニングされていることがわかります。 したがって、残りの約37%で、すぐに確認できます。 Out-of-Bag評価は、トレーニングを受けていないデータの37%までの基本アルゴリズムの平均評価です。
2.ランダムフォレスト
Leo Breimanは、統計だけでなく機械学習にもアプリケーションブートストラップを見つけました。 彼は、Adele Cutlerとともに、 Hoによって提案されたランダムフォレストアルゴリズムを改良し、CARTに基づく無相関ツリーの構築をランダムな部分空間とバギングの方法と組み合わせて元のバージョンに追加しました。
デシジョンツリーは非常に複雑で、任意のサンプルでゼロエラーを達成できるため、バギングの基本的な分類子の優れたファミリです。 ランダム部分空間法は、ツリー間の相関を減らし、過剰適合を防ぎます。 基本的なアルゴリズムは、ランダムに割り当てられる特性記述のさまざまなサブセットでトレーニングされます。
ランダム部分空間法を使用したモデルのアンサンブルは、次のアルゴリズムを使用して構築できます。
- トレーニングするオブジェクトの数を \大N 、および記号の数 \大D 。
- 選択してください \大L アンサンブル内の個々のモデルの数として。
- 個々のモデルごと \大l 選択する \大きいdl(dl<D) の数として \大l 。 通常、すべてのモデルに使用される値は1つだけです。 \大規模なdl 。
- 個々のモデルごと \大l 選択してトレーニングサンプルを作成します \大規模なdl からの兆候 \大D 、モデルをトレーニングします。
- 次に、アンサンブルモデルを新しいオブジェクトに適用するには、個々の結果を結合します \大L 多数決または事後確率の組み合わせによるモデル。
アルゴリズム
で構成されるランダムフォレストを構築するためのアルゴリズム \大N 次のようなツリー:
- それぞれについて \大n=1、\ドット、N :
- サンプルを生成する \大きいXn ブートストラップを使用します。
- 決定的なツリーを構築する \大bn サンプルごと \大きいXn :
-指定された基準に従って、最適な属性を選択し、それによってツリー内にパーティションを作成し、選択が完了するまで続けます。
-ツリーが構築されますが、各シートにはもうありません \大きいn\テキストmin オブジェクトまたは特定のツリーの高さに達するまで
-各パーティションで、最初に選択されます \大m からのランダムな兆候 \大n ソース
そして、サンプルの最適な分離がそれらの間でのみ求められます。
最終分類子 largea(x)= frac1N sumNi=1bi(x) 、簡単な言葉で-キャッシフィケーション問題については、多数決による解決策を選択し、回帰問題では平均による解決策を選択します。
分類の問題を取り入れることをお勧めします \大m= sqrtn 、および回帰タスクで- \大m= fracn3 どこで \大n -標識の数。 また、各シートに1つのオブジェクトが存在するまで、および各シートに5つのオブジェクトが存在するまでの回帰問題では、分類問題で各ツリーを構築することをお勧めします。
したがって、ランダムフォレストは決定木の上でバギングしており、トレーニング中に各パーティションに対して、属性のランダムサブセットから属性が選択されます。
決定木とバギングとの比較
回帰タスクの決定木、バギング、およびランダムフォレストを比較するためのコード from __future__ import division, print_function
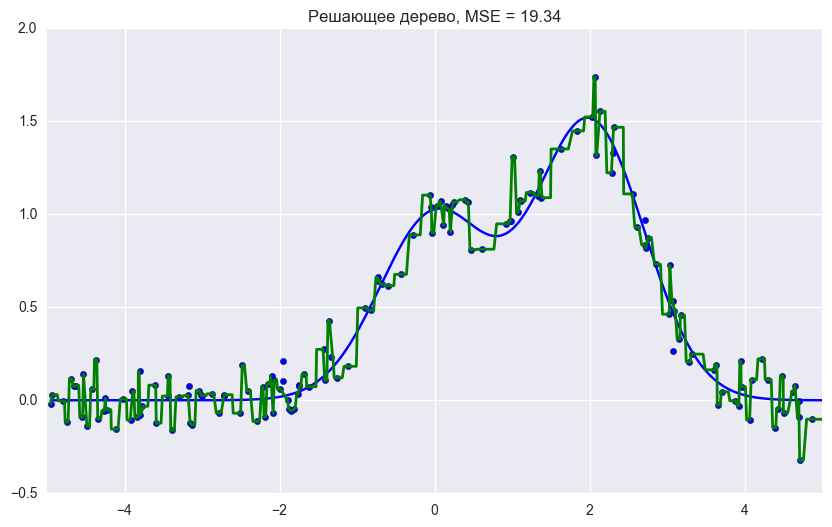


グラフとMSEエラー値からわかるように、10本のツリーのランダムフォレストは、単一のツリーまたは10本の決定ツリーのバギングよりも良い結果をもたらします。 ランダムフォレストと決定木のバギングの主な違いは、フィーチャのランダムサブセットがランダムフォレストで選択され、ノードを分割するための最適な機能は、すべての関数がノードの分離と見なされるバギングとは異なり、フィーチャのサブセットから決定されることです。
分類タスクでランダムフォレストとバギングの利点を確認することもできます。
分類問題の決定木、バギングおよびランダムフォレストを比較するためのコード from sklearn.ensemble import RandomForestClassifier, BaggingClassifier from sklearn.tree import DecisionTreeClassifier from sklearn.datasets import make_circles from sklearn.cross_validation import train_test_split import numpy as np from matplotlib import pyplot as plt plt.style.use('ggplot') plt.rcParams['figure.figsize'] = 10, 6 %matplotlib inline np.random.seed(42) X, y = make_circles(n_samples=500, factor=0.1, noise=0.35, random_state=42) X_train_circles, X_test_circles, y_train_circles, y_test_circles = train_test_split(X, y, test_size=0.2) dtree = DecisionTreeClassifier(random_state=42) dtree.fit(X_train_circles, y_train_circles) x_range = np.linspace(X.min(), X.max(), 100) xx1, xx2 = np.meshgrid(x_range, x_range) y_hat = dtree.predict(np.c_[xx1.ravel(), xx2.ravel()]) y_hat = y_hat.reshape(xx1.shape) plt.contourf(xx1, xx2, y_hat, alpha=0.2) plt.scatter(X[:,0], X[:,1], c=y, cmap='autumn') plt.title(" ") plt.show() b_dtree = BaggingClassifier(DecisionTreeClassifier(),n_estimators=300, random_state=42) b_dtree.fit(X_train_circles, y_train_circles) x_range = np.linspace(X.min(), X.max(), 100) xx1, xx2 = np.meshgrid(x_range, x_range) y_hat = b_dtree.predict(np.c_[xx1.ravel(), xx2.ravel()]) y_hat = y_hat.reshape(xx1.shape) plt.contourf(xx1, xx2, y_hat, alpha=0.2) plt.scatter(X[:,0], X[:,1], c=y, cmap='autumn') plt.title("( )") plt.show() rf = RandomForestClassifier(n_estimators=300, random_state=42) rf.fit(X_train_circles, y_train_circles) x_range = np.linspace(X.min(), X.max(), 100) xx1, xx2 = np.meshgrid(x_range, x_range) y_hat = rf.predict(np.c_[xx1.ravel(), xx2.ravel()]) y_hat = y_hat.reshape(xx1.shape) plt.contourf(xx1, xx2, y_hat, alpha=0.2) plt.scatter(X[:,0], X[:,1], c=y, cmap='autumn') plt.title(" ") plt.show()
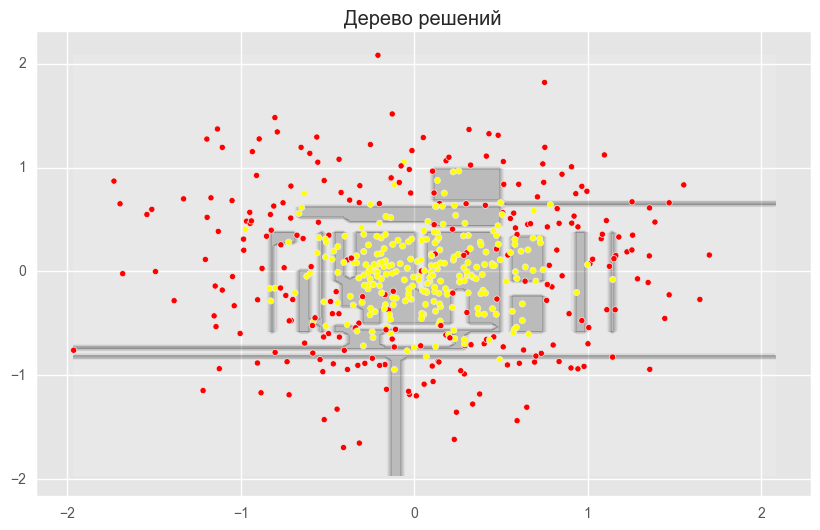
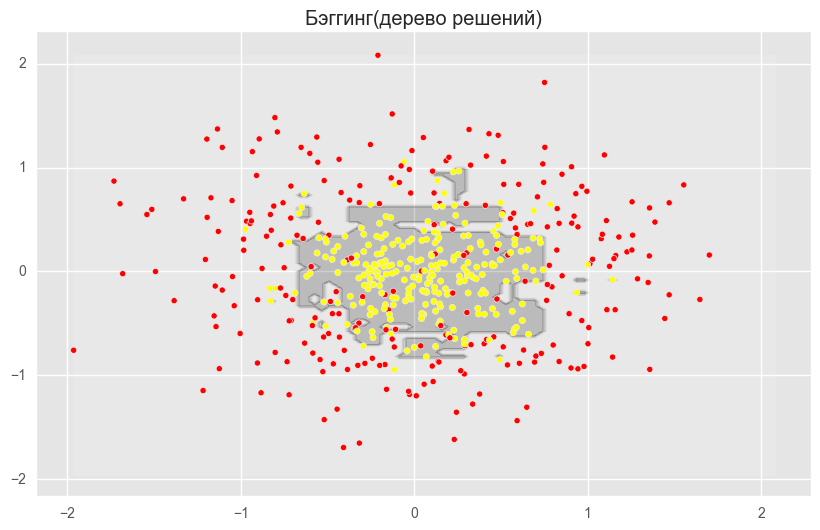
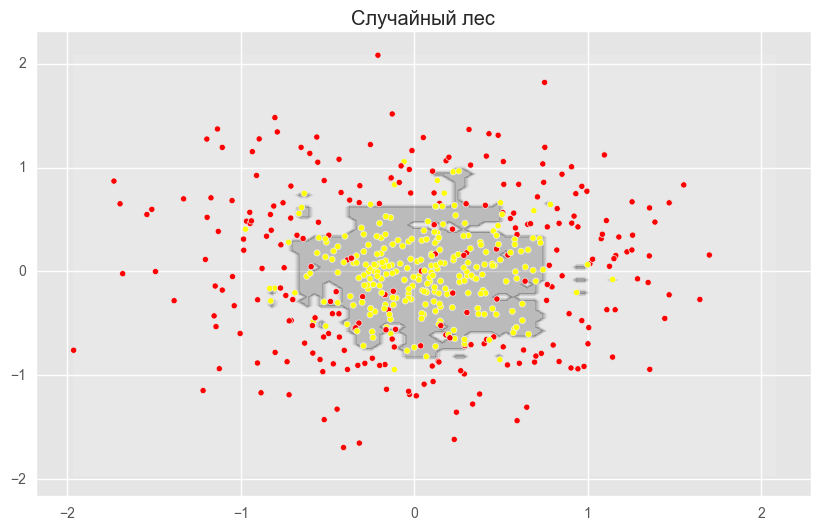
上記の図は、ディシジョンツリーの境界線が非常に「引き裂かれ」ており、再トレーニングと弱い一般化能力を示す多くの鋭いコーナーがあることを示しています。 バギングとランダムフォレストでは、境界は非常に滑らかで、再トレーニングの兆候はほとんどありません。
それでは、正解の割合を増やすことができるパラメーターを把握してみましょう。
パラメータ
ランダムフォレストメソッドは、RandomForestClassifierとRandomForestRegressorの2つのクラスによってscikit-learn機械学習ライブラリに実装されています。
回帰タスクのランダムフォレストパラメーターの完全なリスト:
class sklearn.ensemble.RandomForestRegressor( n_estimators — "" ( – 10) criterion — , ( — "mse" , "mae") max_features — , . , : "auto" ( ), "sqrt", "log2". "auto". max_depth — ( ) min_samples_split — , . ( — 2) min_samples_leaf — . ( — 1) min_weight_fraction_leaf — ( ) ( ) max_leaf_nodes — ( ) min_impurity_split — ( 1-7) bootstrap — ( True) oob_score — out-of-bag R^2 ( False) n_jobs — ( 1, -1, ) random_state — ( , , int verbose — ( 0) warm_start — ( False) )
分類タスクでは、すべてがほぼ同じです。RandomForestClassifierとRandomForestRegressorを区別するパラメーターのみを指定します。
class sklearn.ensemble.RandomForestClassifier( criterion — , "gini" ( "entropy") class_weight — ( 1, , "balanced", ; "balanced_subsample", . )
次に、モデルを構築するときに注意する価値があるいくつかのパラメーターを検討します。
- n_estimators-「フォレスト」内の木の数
- 基準-サンプルを上部で分割するための基準
- max_features-ブレークが検索されるフィーチャの数
- min_samples_leaf-シート内のオブジェクトの最小数
- max_depth-最大ツリー深度
実際の問題でランダムフォレストの使用を検討する
これを行うには、顧客を解雇するタスクを含む例を使用します。 これは分類の問題なので、精度メトリックを使用してモデルの品質を評価します。 まず、最も単純な分類器を構築します。これがベースラインになります。 簡単にするために数字のみを使用しています。
ランダムフォレストのベースラインを構築するためのコード import pandas as pd from sklearn.model_selection import cross_val_score, StratifiedKFold, GridSearchCV from sklearn.metrics import accuracy_score
91.21%, , .
:
import matplotlib.pyplot as plt plt.style.use('ggplot') %matplotlib inline fig, ax = plt.subplots(figsize=(8, 4)) ax.plot(trees_grid, train_acc.mean(axis=1), alpha=0.5, color='blue', label='train') ax.plot(trees_grid, test_acc.mean(axis=1), alpha=0.5, color='red', label='cv') ax.fill_between(trees_grid, test_acc.mean(axis=1) - test_acc.std(axis=1), test_acc.mean(axis=1) + test_acc.std(axis=1), color='#888888', alpha=0.4) ax.fill_between(trees_grid, test_acc.mean(axis=1) - 2*test_acc.std(axis=1), test_acc.mean(axis=1) + 2*test_acc.std(axis=1), color='#888888', alpha=0.2) ax.legend(loc='best') ax.set_ylim([0.88,1.02]) ax.set_ylabel("Accuracy") ax.set_xlabel("N_estimators")
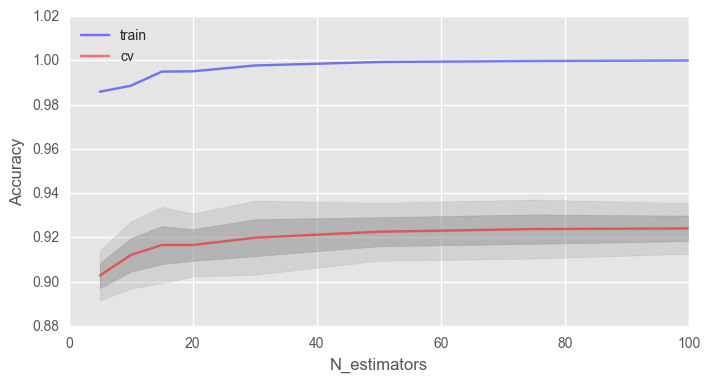
, , , .
, 100% , . , .
– max_depth . ( - 100)
fig, ax = plt.subplots(figsize=(8, 4)) ax.plot(max_depth_grid, train_acc.mean(axis=1), alpha=0.5, color='blue', label='train') ax.plot(max_depth_grid, test_acc.mean(axis=1), alpha=0.5, color='red', label='cv') ax.fill_between(max_depth_grid, test_acc.mean(axis=1) - test_acc.std(axis=1), test_acc.mean(axis=1) + test_acc.std(axis=1), color='#888888', alpha=0.4) ax.fill_between(max_depth_grid, test_acc.mean(axis=1) - 2*test_acc.std(axis=1), test_acc.mean(axis=1) + 2*test_acc.std(axis=1), color='#888888', alpha=0.2) ax.legend(loc='best') ax.set_ylim([0.88,1.02]) ax.set_ylabel("Accuracy") ax.set_xlabel("Max_depth")
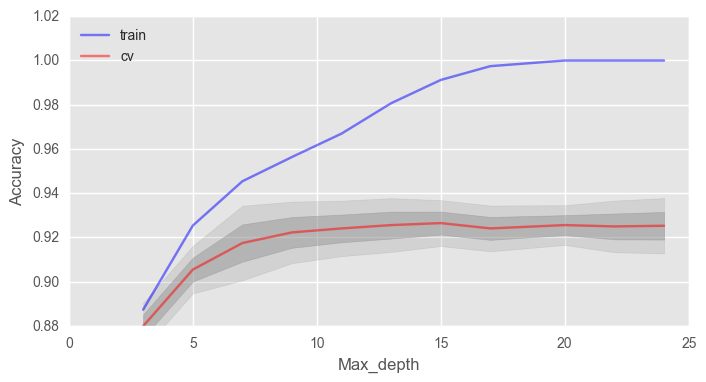
max_depth , . .
min_samples_leaf , .
fig, ax = plt.subplots(figsize=(8, 4)) ax.plot(min_samples_leaf_grid, train_acc.mean(axis=1), alpha=0.5, color='blue', label='train') ax.plot(min_samples_leaf_grid, test_acc.mean(axis=1), alpha=0.5, color='red', label='cv') ax.fill_between(min_samples_leaf_grid, test_acc.mean(axis=1) - test_acc.std(axis=1), test_acc.mean(axis=1) + test_acc.std(axis=1), color='#888888', alpha=0.4) ax.fill_between(min_samples_leaf_grid, test_acc.mean(axis=1) - 2*test_acc.std(axis=1), test_acc.mean(axis=1) + 2*test_acc.std(axis=1), color='#888888', alpha=0.2) ax.legend(loc='best') ax.set_ylim([0.88,1.02]) ax.set_ylabel("Accuracy") ax.set_xlabel("Min_samples_leaf")
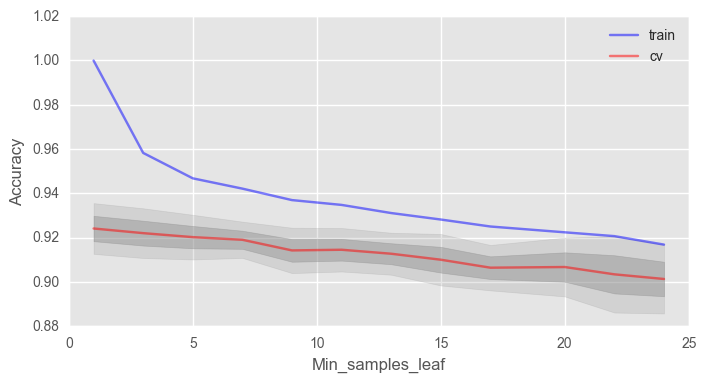
, 2% 92%.
max_features . √n , n — . , 4 .
fig, ax = plt.subplots(figsize=(8, 4)) ax.plot(max_features_grid, train_acc.mean(axis=1), alpha=0.5, color='blue', label='train') ax.plot(max_features_grid, test_acc.mean(axis=1), alpha=0.5, color='red', label='cv') ax.fill_between(max_features_grid, test_acc.mean(axis=1) - test_acc.std(axis=1), test_acc.mean(axis=1) + test_acc.std(axis=1), color='#888888', alpha=0.4) ax.fill_between(max_features_grid, test_acc.mean(axis=1) - 2*test_acc.std(axis=1), test_acc.mean(axis=1) + 2*test_acc.std(axis=1), color='#888888', alpha=0.2) ax.legend(loc='best') ax.set_ylim([0.88,1.02]) ax.set_ylabel("Accuracy") ax.set_xlabel("Max_features")
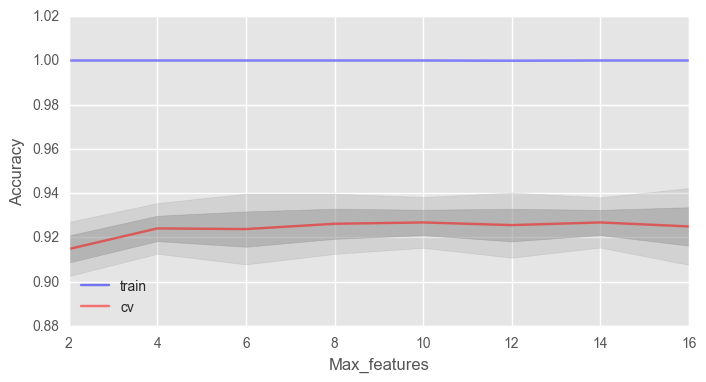
— 10, .
, . GridSearchCV .
, — 92.83% 'max_depth': 15, 'max_features': 7, 'min_samples_leaf': 3 .
V のR F (X )= ρ (X )σ 2(X )
ここに- ρ (x )は、平均化に使用される2つのツリー間のサンプルの相関です。
ρ (X )= C O R R [ T (X 、Θ 1(Z ))、T (X 2、Θ 2(Z ))] 、
どこで Θ 1(Z ) そして Θ2(Z) – Z
σ2(x) — :σ2(x)=VarT(x;Θ(X)
ρ(X) , N- . . , x で ρ(x) . ρ(x) , x , Z , . , Z そして Θ 。
, 0, — .
, ( m ), , , .
The Elements of Statistical Learning (Trevor Hastie, Robert Tibshirani Jerome Friedman) , .
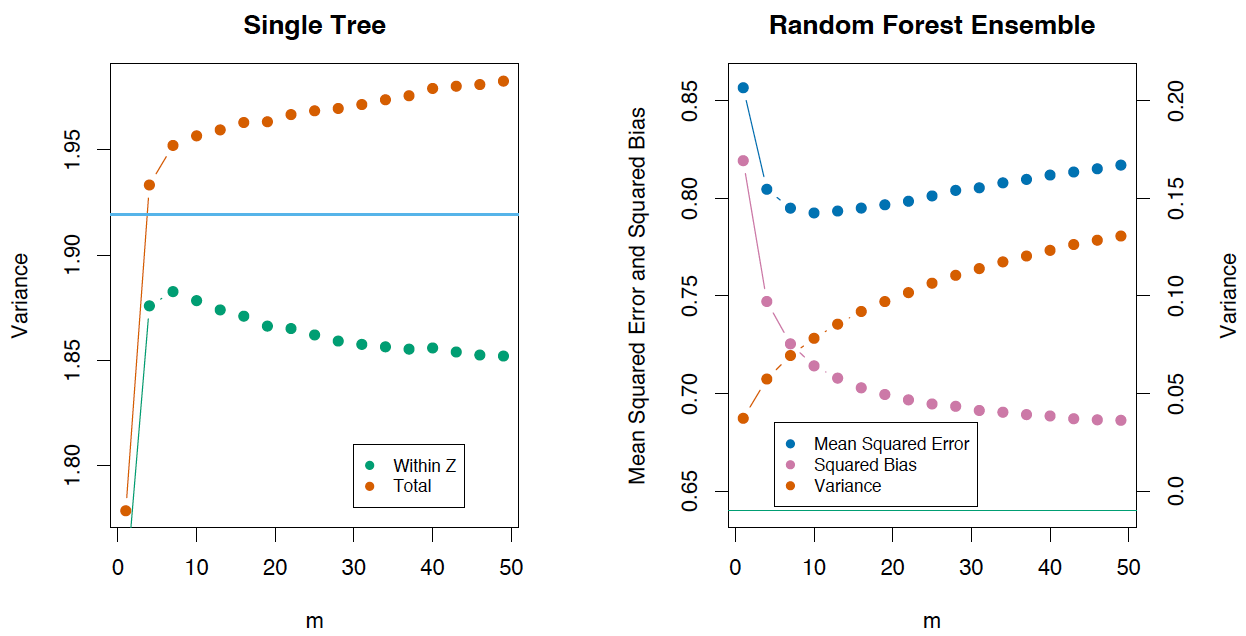
, , T(x,Θ(Z)) :
Bias=μ(x)−EZfrf(x)=μ(x)−EZEΘ|ZT(x,Θ(Z))
( ), «» (unprunned) , . , , , .
(Extremely Randomized Trees) , . , , , , . .
scikit-learn ExtraTreesClassifier ExtraTreesRegressor . , .
k-
. , , . , . .
. させる Tn(x) — n(x) - , x 。 x , Tn(x) 。
bn(x)=l∑i=1wn(x,xi)yi,
どこで
wn(x,xi)=[Tn(x)=Tn(xi)]∑lj=1[Tn(x)=Tn(xj)]
an(x)=1N∑Nn=1∑li=1wn(x,xi)yi=∑li=1(1N∑Nj=1wn(x,xj))yi
, . , Tn(x) , , . , , T1(x),…,Tn(x) 。 .
The Elements of Statistical Learning k- .
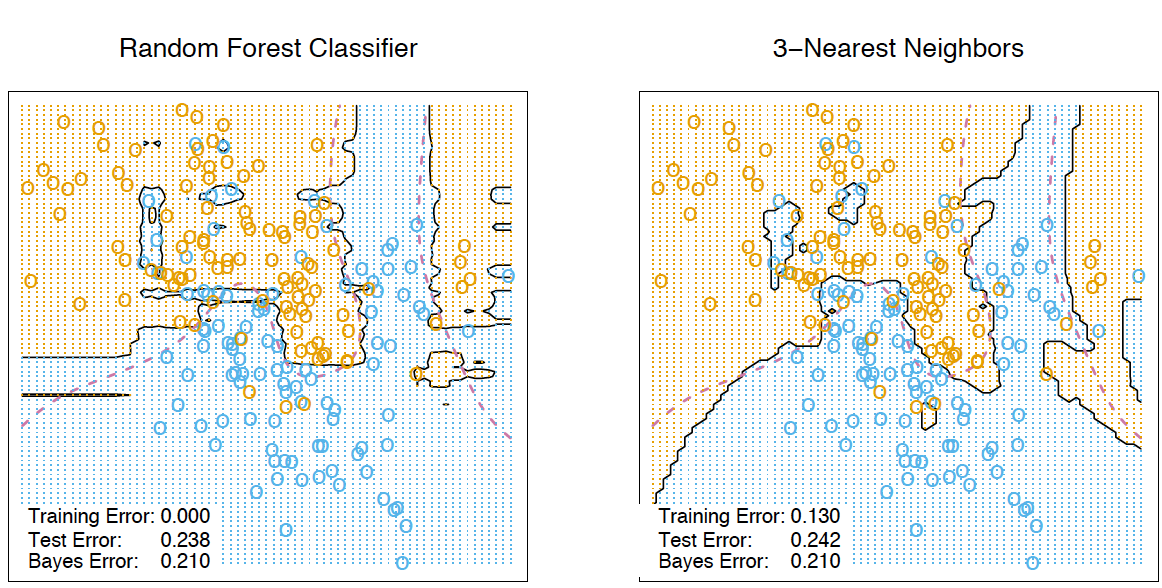
, . RandomTreesEmbedding . , , , , . , 1, , 0. . / . , , .
3.
, , . , . .
, «» , «». .
( ), , /. ( (Gini impurity)) — , , .
. , , out-of-bag . - ( ) , , ́ . ( mse ) , . , , . 0 () 1 (). . , , .
.
VIT=∑i∈BTI(yi=ˆyTi)|BT|−∑i∈BTI(yi=ˆyTi,πj)|BT|
ˆy(T)i=fT(xi) — /
ˆy(T)i,πj=fT(xi,πj) — /
xi,πj=(xi,1,…,xi,j−1,xπj(i),j,xi,j+1,…,xi,p)
, VI(T)(xj)=0 もし Xj T
:
—
VI(xj)=∑NT=1VIT(xj)N
—
zj=VI(xj)ˆσ√N
例
Booking.com TripAdvisor.com. — ( ) — , .. — .
from __future__ import division, print_function

, / . , - . / .
4.
長所 :
— , ;
— -
— ( ) ,
— , « ». «» 0.5 3%
—
— ,
— , , , ,
—
— ; ,
— ,
— , , ( )
— , , , ,
— .
短所 :
— ,
— (p-values),
— , (, Bag of words)
— , ( , )
— ,
— , , : , , ( )
— , ,
— . O(NK) , K — .
5.
, .
– . - ( ).
6.
– Open Machine Learning Course. Topic 5. Bagging and Random Forest ( )
–
– 15 “ Elements of Statistical Learning ” Jerome H. Friedman, Robert Tibshirani, and Trevor Hastie
–
– - scikit-learn
– ( GitHub).
– " " (. )
yorko ( ). – vradchenko ( ). bauchgefuehl ( ) .