learnopengl。 レッスン1.8-座標系

前のレッスンでは、変換行列で頂点を変換することで得られる利点について学びました。 OpenGLは、シェーダーの開始後に表示するすべての頂点が、正規化されたデバイス座標（NDC）にあると想定しています。 これは、各頂点のx、y、z座標が-1.0〜1.0の間でなければならないことを意味します。 この範囲外の座標は表示されません。 通常、自分で設定した範囲の座標を指定し、頂点シェーダーでこれらの座標をNDCに変換します。 次に、これらのNDCはラスタライザーに渡されて、画面の2次元座標/ピクセルに変換されます。

座標を正規化してからスクリーン座標に変換することは、通常、段階的に行われます。最終的にスクリーン座標に変換する前に、オブジェクトの頂点をいくつかの座標系に変換します。 いくつかの中間座標系を介した座標変換の利点は、特定のシステムで一部の操作/計算が簡単に実行できることです。これはすぐに明らかになります。 合計で、私たちにとって重要な5つの異なる座標系があります。

1. ローカル空間（またはオブジェクト空間）
2. ワールドスペース
3. ビューのスペース（またはオブザーバー）
4. クリッピングスペース
5. スクリーンスペース

ピークは、フラグメントになる前に、これらすべての異なる状態に変換されます。

おそらく今、あなたは各空間または座標系が何であるか完全に混乱しているので、全体像と各空間が実際に何をするかを示すことにより、それらをより理解しやすい形で検討します。

一般的なスキーム

座標をある空間から別の空間に変換するために、いくつかの変換行列を使用しますが、その中で最も重要なのはModel 、 ViewおよびProjection行列です。 頂点の座標はローカル空間でローカル座標として始まり、その後ワールド座標に変換され、次にビューの座標 、 クリッピングに変換され、最後にすべてが画面座標で終了します 。 次の図は、このシーケンスと各変換の動作を示しています。

1. ローカル座標はオブジェクトの座標であり、オブジェクト自体が始まる場所にある参照ポイントを基準にして測定されます
2. 次のステップでは、ローカル座標がワールド空間の座標に変換されます。これは、意味では、より大きな世界の座標です。 これらの座標は、ワールド基準点に関連して測定され、ワー​​ルド空間にある他のすべてのオブジェクトに共通です
3. さらに、各頂点がカメラまたは観測者の視点から見たように見えるように、ワールド座標をビュー空間の座標に変換します
4. 座標がビュー空間に変換されたら、クリッピング座標に投影します。 クリッピング座標は-1.0〜1.0の範囲で有効であり、画面に表示される頂点を決定します。
5. 最後に、ビューポートの変換と呼ばれる変換プロセスで、
   クリッピング座標を-1.0から1.0に変換し、 glViewport関数で指定された画面座標の領域に変換します。

このすべての後、受信した座標はラスタライザーに送信され、それらがフラグメントに変換されます。

おそらく、各座標空間の用途を少し理解しているでしょう。 頂点をこれらの異なる座標空間に変換する理由は、特定の座標系で一部の操作がより理解可能または単純になるためです。

たとえば、ローカル空間でオブジェクトを変更するのが最も合理的であり、他のオブジェクトの位置を考慮した操作の計算は、ワールド座標などで行うのが最適です。 必要に応じて、1つの変換行列を指定できます。これにより、ローカル空間からクリッピング空間に1ステップで座標が変換されますが、これにより柔軟性が失われます。

以下では、各座標系について詳しく説明します。

ローカルスペース

ローカル空間は、オブジェクトに対してローカルな座標系です。 オブジェクト自体と同じポイントで開始します。 モデリングソフトウェアパッケージでBlenderに似たキューブを作成したと想像してください。 アプリケーションの座標内のキューブが別の場所にある場合でも、キューブの開始点はおそらく（0,0,0）にあります。 作成したすべてのモデルに開始点（0,0,0）がある可能性があります。 したがって、モデルのすべての頂点はローカル空間にあります。すべての座標はオブジェクトに対してローカルです。

使用したコンテナの頂点は、-0.5から0.5の間の座標を使用して決定され、開始点は0.0です。 これらはローカル座標です。

ワールドスペース

すべてのオブジェクトをアプリケーションに直接インポートする場合、それらはおそらくワールド参照ポイント（0,0,0）の近くで互いの上に積み上げられますが、これは望みどおりではありません。 より大きなスペースに配置するには、各オブジェクトの位置を決定する必要があります。 ワールド空間の座標、これはまさにその名前のとおりです：（ゲーム）ワールドに対するすべての頂点の座標。 これは、空間に分布するように（そしてできれば現実的に）オブジェクトが変換されるのを見たい座標空間です。 オブジェクトの座標は、ローカル空間からワールド空間に変換されます。 これは、 モデルマトリックスを介して行われます。

モデルマトリックスは、オブジェクトを移動、スケーリング、および/または回転して、オブジェクトが存在するべき位置/方向でワールド空間に配置するマトリックスです。 これは、拡大された（ローカルスペースでは大きすぎた）建物を郊外に移動し、Y軸に沿ってわずかに左に曲がって隣接する家にぴったり合う建物の変形として想像してください。 コンテナをシーン内で移動した前のレッスンのマトリックスを、一種のモデルマトリックスとして認識することができます。 その助けを借りて、シーン/世界のさまざまな場所に配置するために、コンテナのローカル座標を再集計しました。

表示スペース

ビュースペースは、通常OpenGL カメラと呼ばれるものです（ カメラスペースまたはオブザーバー スペースとも呼ばれます ）。 ビュー空間は、世界座標をユーザーが正面から見ているように見える座標に変換した結果です。 したがって、ビュースペースは、カメラのビューファインダーを通して見えるスペースです。 これは通常、一部のオブジェクトがカメラの前にあるようなシーンのシフトと回転の組み合わせによって実現されます。 これらの結合された変換は、通常、ワールド座標をビュー空間に変換するビューマトリックスに格納されます。 次のレッスンでは、このようなビューマトリックスを作成してカメラをシミュレートする方法について広範囲に説明します。

クリッピングスペース

頂点シェーダーが終了すると、OpenGLはすべての座標が特定の範囲内にあり、その境界を超えるすべてのものが切断されることを予期します。 カットオフ座標は破棄され、残りの座標は画面上に表示されるフラグメントになります。 それがクリッピングスペースの名前の由来です。

[-1.0、1.0]の範囲の値ですべての可視座標を設定することは実際には直感的ではないため、作業のために独自の座標セットを定義し、OpenGLが期待するようにNDCに変換します。

ビュー空間からクリッピング空間に座標を変換するために、たとえば各軸に沿って-1000から1000までの座標の範囲を定義する、いわゆる射影行列を定義します。 射影行列は、この範囲の座標をデバイスの正規化された座標（-1.0、1.0）に変換します。 指定された間隔外のすべての座標はエリア[-1.0、1.0]に該当しないため、切り取られます。 射影行列によって設定された範囲では、座標（1250、500、750）は表示されません。Xコンポーネントが境界を超えるため、NDCで1.0を超える値に変換され、したがって頂点がクリップされるためです。 。

三角形などのプリミティブ全体ではなく、その一部のみがカットオフボリュームの外側にある場合、OpenGLは完全にカットオフ範囲にある1つ以上の三角形の形でこの三角形を再構築することに注意してください。

投影行列によって定義されるこの表示ボリュームは、錐台ピラミッドと呼ばれ、このピラミッドに入る各座標はユーザーの画面に表示されます。 特定の範囲の座標をデバイスの正規化された座標（NDC）に変換するプロセス全体は、プロジェクションマトリックスが3D座標をデバイスの単純な2Dに変換された正規化された座標に投影するため、プロジェクションと呼ばれます。

すべての頂点の座標がクリッピングスペースに転送されるとすぐに、 パースペクティブ分割と呼ばれる最終操作が実行されます。 その中で、頂点位置ベクトルのx、y、z成分をベクトルwの同次成分で除算します。 パースペクティブ除算は、クリッピングスペースの4D座標をデバイスの3次元の正規化された座標に変換します。 このステップは、各頂点シェーダーの完了後に自動的に実行されます。

この段階の後、受信した座標（ glViewport設定を使用）は画面座標に表示され、フラグメントに変わります。

投影行列は、ビュー座標をクリッピング座標に変換し、2つの異なる形状をとることができます。各形状は、独自の特別な切頭ピラミッドを定義します。 正射投影行列またはパースペクティブを作成できます。

正投影

正投影図法は、平行四辺形の形で切り捨てられたピラミッドを定義します。平行四辺形は、ボリュームの外側のすべての頂点がクリップされるクリッピングスペースです。 正射投影行列を作成するとき、表示されるクリッピングピラミッドの幅、高さ、および長さを指定します。 投影行列によってクリッピングスペースに変換された後、ピラミッドで囲まれたボリュームに含まれるすべての座標はクリップされません。 切り捨てられたピラミッドは、コンテナのように見えます。

角錐台は、可視座標の領域を定義し、幅、高さ、 近接および遠方の平面によって定義されます。 ニアプレーンの前にある座標は、リアプレーンの後ろにある座標と同じように切り取られます。 正投影の角錐台は、それに含まれる座標をデバイスの正規化された座標に直接変換し、ベクトルのwコンポーネントは使用されません。 wコンポーネントが1.0の場合、遠近法による分割は座標値を変更しません。

正射投影行列を作成するには、 glm :: orthoと呼ばれる組み込みGLMライブラリ関数を使用します。

glm::ortho(0.0f, 800.0f, 0.0f, 600.0f, 0.1f, 100.0f ); 

最初の2つのパラメーターは、切り捨てられたピラミッドの左右の座標を決定し、3番目と4番目のパラメーターは、ピラミッドの下限と上限を指定します。 これらの4つのポイントは、ニアプレーンとファープレーンの寸法を設定し、5番目と6番目のパラメーターはそれらの間の距離を示します。 この特定の投影行列は、x、y、およびzの値の範囲に入るすべての座標をデバイスの正規化された座標に変換します。

正射投影行列は、座標である2次元平面（ディスプレイ）に直接表示されますが、実際には、 透視図を考慮していないため、直接投影は非現実的な結果をもたらします。 これにより、 透視投影行列が修正されます。

透視投影

現実世界を見たことがあれば、遠くにあるオブジェクトがはるかに小さく見えることにおそらく気づいたでしょう。 私たちはこの奇妙な効果の視点を呼び出します 。 次の図に示すように、無限の高速道路または鉄道の終点を見ると、特に目立ちます。

ご覧のように、視点から見ると、線がより収束するほど、線はより遠くにあるように見えます。 これはまさに、透視投影がシミュレートしようとしている効果であり、透視投影のマトリックスを通じて達成されます。 射影行列は、切り捨てられたピラミッドの指定された範囲をクリッピングスペースにマッピングし、同時に、頂点が観測者から遠ざかるほどこのw値が大きくなるように各頂点のwコンポーネントを操作します。 座標をクリッピングスペースに変換した後、それらはすべて-wからwの範囲に入ります（この範囲外の頂点はクリップされます）。 OpenGLでは、頂点シェーダーの最終出力が-1.0〜1.0の座標であることが必要です。 したがって、座標がクリッピング空間にある場合、遠近法の分割がそれらに適用されます。

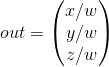
頂点座標の各コンポーネントは、ビューアーからの距離に比例して座標値を減らす独自のwコンポーネントに分割されます。 これは、透視投影に役立つため、wコンポーネントの重要性のもう1つの理由です。 この後に取得される座標は、デバイスの正規化された空間にあります。 直交射影行列がどのように計算されるかを理解することに興味がある場合（そして数学を恐れることはありません）、Songho によるこの素晴らしい記事をお勧めします。

GLMライブラリの透視投影行列は、次のように作成できます。

 glm::mat4 proj = glm::perspective( 45.0f, (float)width/(float)height, 0.1f, 100.0f); 

glm ::パースペクティブは、目に見えるスペースを定義する切り捨てられたピラミッドを作成し、その外側にあり、クリッピングスペースのボリュームに入らないものはすべて切り取られます。 予想される切り捨てられたピラミッドは、台形のボックスとして表すことができ、各内部座標はクリッピングスペース内のポイントにマッピングされます。 パースペクティブトランケートピラミッドの画像を以下に示します。

最初のパラメーターは、「 視野 」を意味するfov （視野）の値を設定し、可視領域の大きさを決定します。 現実的な表現のために、このパラメーターは通常45.0fに設定されますが、同様の運命のスタイルを得るために、大きな値を設定することもできます。 2番目のパラメーターは、ビューポートの幅を高さで割ることによって計算されるアスペクト比を設定します。 3番目と4番目のパラメーターは、角錐台の近くの平面と遠くの平面を定義します。 通常、最も近い距離を0.1fに設定し、最も遠い距離を100.0fに設定します。 ニアプレーンとファープレーンの間に位置し、切り捨てられたピラミッドのボリューム内にあるすべての頂点が視覚化されます。

投影行列のニアプレーンまでの距離が大きすぎると（10.0fなど）、OpenGLはカメラの隣にあるすべての座標（0.0〜10.0f）を切り取ります。これにより、ビデオゲームでおなじみの視覚効果が得られます。近づきすぎた場合は、一部のオブジェクトを透かして見ます。

直交投影を使用する場合、各頂点座標は、仮想の遠近法による分割なしでクリッピング空間に直接マップされます（遠近法による分割は実行されますが、wコンポーネントは結果に影響を与えないため（1のまま）、効果はありません）。 正射投影では遠近法が考慮されないため、さらに配置されたオブジェクトは小さく見えず、奇妙な視覚的印象を与えます。 このため、正射投影法は、主に2Dレンダリングや、建築や工学のさまざまな用途に使用されますが、遠近法による歪みがないことが望まれます。 Blender for 3Dモデリングなどのアプリケーションでは、各オブジェクトの測定値と比率をより正確に表示するため、モデリング中に正投影が使用されることがあります。 以下は、Blenderの両方の投影方法の比較です。

透視投影では、削除された頂点がはるかに遠くなることがわかりますが、正投影では、頂点の削除速度は同じであり、観測者までの距離に依存しません。

すべてをまとめる

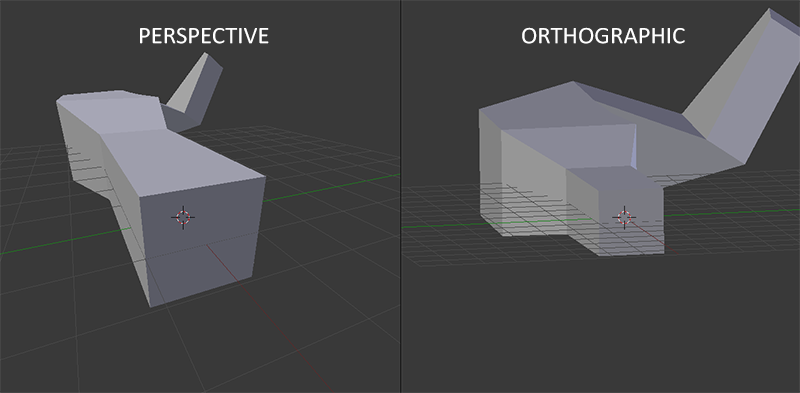
上記の各ステップ（モデル、ビュー、投影マトリックス）の変換マトリックスを作成します。 頂点座標は、次のようにクリッピングスペースの座標に変換されます。

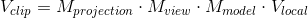
行列の乗算の順序が逆になっていることに注意してください（行列の乗算は右から左に読み取らなければならないことに注意してください）。 結果の頂点座標は、組み込み変数gl_Positionを使用して頂点シェーダーで割り当てる必要があります。その後、OpenGLは自動的に遠近法の分割とクリッピングを実行します。

それで何？
頂点シェーダー出力の座標はクリッピング空間内にある必要があります。これは、変換マトリックスの助けを借りて達成したものです。 OpenGLは、クリッピングスペースの座標の透視分割を実行して、それらを正規化されたデバイス座標に変換します
次に、OpenGLはglViewPortのパラメーターを使用して、デバイスの正規化された座標を、各座標が画面上のポイントに対応する画面座標にマッピングします（この場合、これは800x600の領域です）。 このプロセスはビューポート変換と呼ばれます。

このトピックを理解するのは難しいので、各スペースが何に使用されているのかまだよくわからない場合は心配する必要はありません。

以下に、これらの座標空間を効果的に使用する方法を示します。今後のレッスンでは十分な例があります。

3Dに移動

3D座標を2D座標に変換する方法がわかったので、これまでに示した欠陥のある2D平面ではなく、オブジェクトを実際の3Dオブジェクトとして表示し始めることができます。

3Dでの描画を開始するには、最初にモデルマトリックスを作成します。 モデルマトリックスは、オブジェクトのすべての頂点をグローバルワールド空間に変換するために適用するシフト、スケーリング、および/または回転で構成されます。 X軸に沿って回転させて、平面が床に横たわっているように見えるようにして、平面を少し変更しましょう。 モデルのマトリックスは次のようになります。

 glm::mat4 model; model = glm::rotate(model, -55.0f, glm::vec3(1.0f, 0.0f, 0.0f); 

頂点の座標にこのモデルのマトリックスを掛けて、それらをワールド座標に変換します。 床に横たわっている飛行機は、このように世界空間の飛行機を表しています。

次に、ビューマトリックスを作成する必要があります。 オブジェクトが表示されるようにするには、シーン内を少し戻す必要があります（ワールド空間での観測者の視点は原点（0,0,0）にあるため）。 シーン内を移動するには、次のことを考慮してください。

カメラを後方に移動することは、シーン全体を前方に移動することと同じです。

これがまさにビューマトリックスの機能です。シーン全体を、カメラを移動したい方向と反対の方向に移動します。 後方に移動する必要があり、OpenGLが正しい座標系を使用するため、z軸の正の方向に移動する必要があります。 これを行うには、シーン全体をz軸の負の側にシフトします。 これは、私たちが後退しているような印象を与えます。

正しい座標系

慣例により、OpenGLは正しい座標系です。 , X , Y , Z (. ). , , Z . :

, , :

• Y .
• .
• .
• 90 .

, X, — Y, z. , , Z . DirectX. , OpenGL ( ).

. :

 glm::mat4 view; //  ,        ,      view = glm::translate(view, glm::vec3(0.0f, 0.0f, -3.0f)); 

, — . , :

 glm::mat4 projection; projection = glm::perspective(45.0f, screenWidth / screenHeight, 0.1f, 100.0f); 

GLM. fov 45 , GLM fov , glm::radians(45.0).

, , . uniform :

 #version 330 core layout (location = 0) in vec3 position; ... uniform mat4 model; uniform mat4 view; uniform mat4 projection; void main() { // ,       gl_Position = projection * view * model * vec4(position, 1.0f); ... } 

( , ):

 GLint modelLoc = glGetUniformLocation(ourShader.Program, "model"); glUniformMatrix4fv(modelLoc, 1, GL_FALSE, glm::value_ptr(model)); ... //        

, , , :

• .
• .
• ( ).

, :

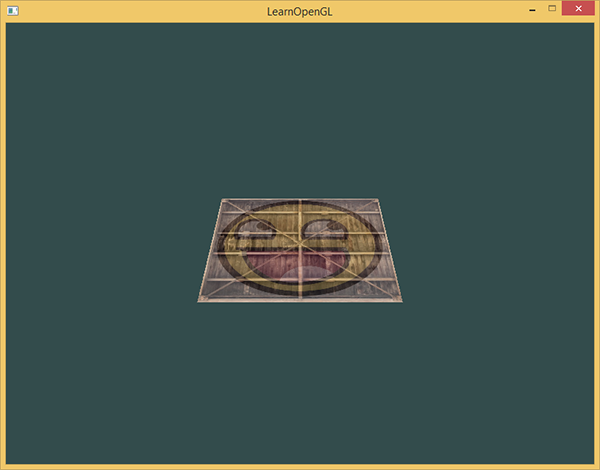
3D-, - . , , .

3D

2D-, 3D-, 2D- 3D-.

36 (6 * 2 * 3 ). 36 , . , , .

«» , glVertexAttribPointer:

 // Position attribute glVertexAttribPointer(0, 3, GL_FLOAT, GL_FALSE, 5 * sizeof(GLfloat), (GLvoid*)0); ... // TexCoord attribute glVertexAttribPointer(2, 2, GL_FLOAT, GL_FALSE, 5 * sizeof(GLfloat), (GLvoid*)(3 * sizeof(GLfloat))); 

:

 model = glm::rotate(model, (GLfloat)glfwGetTime() * 50.0f, glm::vec3(0.5f, 1.0f, 0.0f)); 

glDrawArrays, 36 .

 glDrawArrays(GL_TRIANGLES, 0, 36); 

- :

, - . . , , OpenGL --, , , . - , .

, OpenGL Z- , OpenGL , , . Z-, OpenGL .

Z-

OpenGL Z-, . GLFW ( , ). ( z-) , , OpenGL Z-, , . OpenGL .

, , OpenGL , , - . glEnable . glEnable glDisable / OpenGL. OpenGL /, /. , GL_DEPTH_TEST :

 glEnable(GL_DEPTH_TEST); 

, ( ). , glClear GL_DEPTH_BUFFER_BIT :

 glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT); 

, OpenGL :

以上です！ , , . .

!

, 10 . , . , , . , — , .

-, , . 10 glm::vec3:

 glm::vec3 cubePositions[] = { glm::vec3( 0.0f, 0.0f, 0.0f), glm::vec3( 2.0f, 5.0f, -15.0f), glm::vec3(-1.5f, -2.2f, -2.5f), glm::vec3(-3.8f, -2.0f, -12.3f), glm::vec3( 2.4f, -0.4f, -3.5f), glm::vec3(-1.7f, 3.0f, -7.5f), glm::vec3( 1.3f, -2.0f, -2.5f), glm::vec3( 1.5f, 2.0f, -2.5f), glm::vec3( 1.5f, 0.2f, -1.5f), glm::vec3(-1.3f, 1.0f, -1.5f) }; 

, glDrawArrays 10 , . , 10 . , .

 glBindVertexArray(VAO); for(GLuint i = 0; i < 10; i++) { glm::mat4 model; model = glm::translate(model, cubePositions[i]); GLfloat angle = 20.0f * i; model = glm::rotate(model, angle, glm::vec3(1.0f, 0.3f, 0.5f)); glUniformMatrix4fv(modelLoc, 1, GL_FALSE, glm::value_ptr(model)); glDrawArrays(GL_TRIANGLES, 0, 36); } glBindVertexArray(0); 

, 10 . , :

いいね！ , . , , .

演習

• , GLM projection FOV .
  , , .
• , , . .
• 3- ( 1), , :
  .