大規模クラスターの速度論

まとめ

1. マーティン・クレップマンの致命的な間違い。
   
2. 物理化学反応は数学を行います。
   
3. クラスターの半減期。
   
4. 非線形微分方程式を解くことなく解きます。
   
5. 触媒としてのノード。
   
6. チャートの予測力。
   
7. 1億年。
   
8. 相乗効果。
   

前の記事で、 Brewerの記事と同名の彼の定理について詳しく調べました。 今回は、 Martin Kleppmanの投稿「大規模クラスターでのデータ損失の可能性」の準備を準備します。

この投稿では、著者は次の問題をモデル化しようとします。 データの整合性を確保するために、通常、データ複製方法が使用されます。 この場合、実際には、消去符号化が使用されているかどうかは関係ありません。 元の投稿では、著者は1つのノードが脱落する確率を尋ねてから、次の質問を投げかけます。ノードの数が増えるとデータが脱落する確率はどれくらいですか？

答えはこの写真に示されています：



つまり ノードの数が増えると、失われたデータの数は比例して増加します。

なぜこれが重要なのですか？ 最新のクラスターのサイズを考慮すると、その数は時間とともに継続的に増加していることがわかります。 したがって、合理的な疑問が生じます。データの安全性を心配し、複製係数を上げる価値はありますか？ 結局のところ、これはビジネス、所有コストなどに直接影響します。 また、この例では、数学的には正しいが間違った結果を生成する方法を素晴らしく示すことができます。

クラスターモデリング

計算の不正確さを実証するには、モデルとモデリングが何であるかを理解することが役立ちます。 モデルがシステムの実際の動作を不十分に記述している場合、正しい式を使用しても、間違った結果を簡単に得ることができます。 そして、すべて私たちのモデルは無視できないシステムのいくつかの重要なパラメーターを考慮しないかもしれないという事実のためです。 芸術は、何が重要で何が重要でないかを理解することです。

クラスターの寿命を記述するには、変更のダイナミクスとさまざまなプロセスの相互接続を考慮することが重要です。 これはまさに、元の記事の弱いリンクです。なぜなら、 レプリケーションに関連する機能なしで静的な写真が撮影されました。

ダイナミクスを説明するために、 化学動力学の方法を使用します。粒子の集合の代わりに、ノードの集合を使用します。 私の知る限り、このような形式を使用してクラスターの動作を説明した人はいません。 したがって、私は即興で演奏します。

次の表記法を紹介します。

1. ：クラスターノードの総数
   
2. ：作業ノードの数（使用可能）
   
3. ：問題のあるノードの数（失敗）
   

それからそれは明らかです：


問題のあるノードの数に問題を含めます。ディスクがねじ込まれ、プロセッサ、ネットワークなどが壊れています。 その理由は私にとって重要ではありません。データの内訳とアクセス不能の事実は重要です。 もちろん、将来的には、より微妙なダイナミクスを考慮することもできます。

次に、クラスターノードのブレークダウンと復元のプロセスの運動方程式を記述します。


これらの最も単純な方程式は次のように言います。 最初の方程式は、ノード障害のプロセスを説明しています。 パラメーターに依存せず、孤立ノードの障害を説明します。 他のノードはこのプロセスに関与しません。 プロセス参加者の元の「構成」が左側に使用され、プロセスの製品が右側に使用されます。 速度定数 そして ノードを切断および復元するプロセスの速度特性をそれぞれ設定します。

速度定数の物理的な意味を調べてみましょう。 これを行うには、運動方程式を書きます。


これらの方程式から、定数の意味 そして 。 管理者がいないと仮定し、クラスターがそれ自体を修復しない場合（つまり、 ）、すぐに方程式を取得します：


または


つまり 価値 -これはスペアパーツのクラスターの半減期であり、 。 させる -状態からの単一ノードの特性遷移時間 述べる 、そして -状態からの単一ノードの特性遷移時間 述べる 。 それから


運動方程式を解きます。 可能な限り予測してチューニングするために使用する最も単純な分析依存関係を取得するために、可能な限りコーナーをカットするという予約をすぐに作りたいと思います。

なぜなら 微分方程式の解の数の上限に達したら、準定常状態の方法でこれらの方程式を解きます 。


という事実を考えると （これは非常に合理的な仮定です。それ以外の場合は、より良いハードウェアまたはより高度な管理者を購入する必要があります）、次のようになります。


その回復時間を入れたら 約1週間、死の時 約1年、壊れたノードのシェアを取得します ：

チャンク

で示す -状態への遷移中にノードが落ちた後に複製する必要がある複製されていないチャンクの数 。 次に、チャンクを説明するために、方程式を修正します。


どこで 二次プロセスの複製速度定数、および チャンクの総質量に溶解する健全なチャンクを意味します。

3番目の方程式を明確にする必要があります。 最初のプロセスではなく、2次プロセスについて説明します。


そうした場合、クレップマン曲線が得られますが、これは私の計画には含まれていません。 実際、すべてのノードが回復プロセスに参加し、ノードが多いほど、プロセスは速くなります。 これは、キルされたノードからのチャンクがクラスター全体にほぼ均等に分散されるため、各参加者は 数倍。 これは、強制終了されたノードからのチャンクの最終的な回復速度が、使用可能なノードの数に比例することを意味します。

また、式（3）の左右のスタンド 、同時に使用されません。 この場合、化学者はすぐにそれを言うでしょう 触媒として機能します。 そして、慎重に考えれば、その通りです。

準定常濃度の方法を使用すると、すぐに結果が得られます。


または


驚くべき結果！ つまり 複製する必要があるチャンクの数は、ノードの数に依存しません！ これは、ノード数の増加が結果として生じる反応速度を増加させ（3）、それにより多くの数を補償するという事実によるものです。 ノード 触媒作用！

この値を評価してください。 -チャンクの回復時間。ノードが1つしかないかのように。 ノードで5TBのデータを複製する必要がある場合、バイト単位の複製フローを50MB / sに設定すると、次のようになります。


つまり そして、あなたはデータの安全性を恐れることはできません。 3つのうち1つのチャンクが失われても、データが失われないことを考慮する価値があります。

複製計画

前の計算では、ノードはどの特定のチャンクを複製する必要があるかを即座に認識し、すぐに複製プロセスを開始するという暗黙の仮定をしました。 実際には、これは完全に間違っています。マスターはノードが死んだことを理解する必要があり、次にどの特定のチャンクを複製する必要があるかを理解し、ノードでの複製プロセスを開始する必要があります。 これはすべて瞬時ではなく、時間がかかります。 （スケジューリング）。

遅延を考慮するために、 遷移状態または活性化された複合体の理論を使用します。これは、ポテンシャルエネルギーの多次元表面上の点を通る遷移を表します。 私たちの観点から、いくつかの中間状態が追加されます 、つまり、このチャンクは複製がスケジュールされていますが、複製プロセスはまだ開始されていません。 つまり 次のナノ秒で、レプリケーションは確実に開始されますが、ピコ秒前ではありません。 その後、システムは最終的な形式を取ります。


それを解決すると、次のことがわかります。


準定常濃度の方法を使用して、以下を見つけます。


ここで：


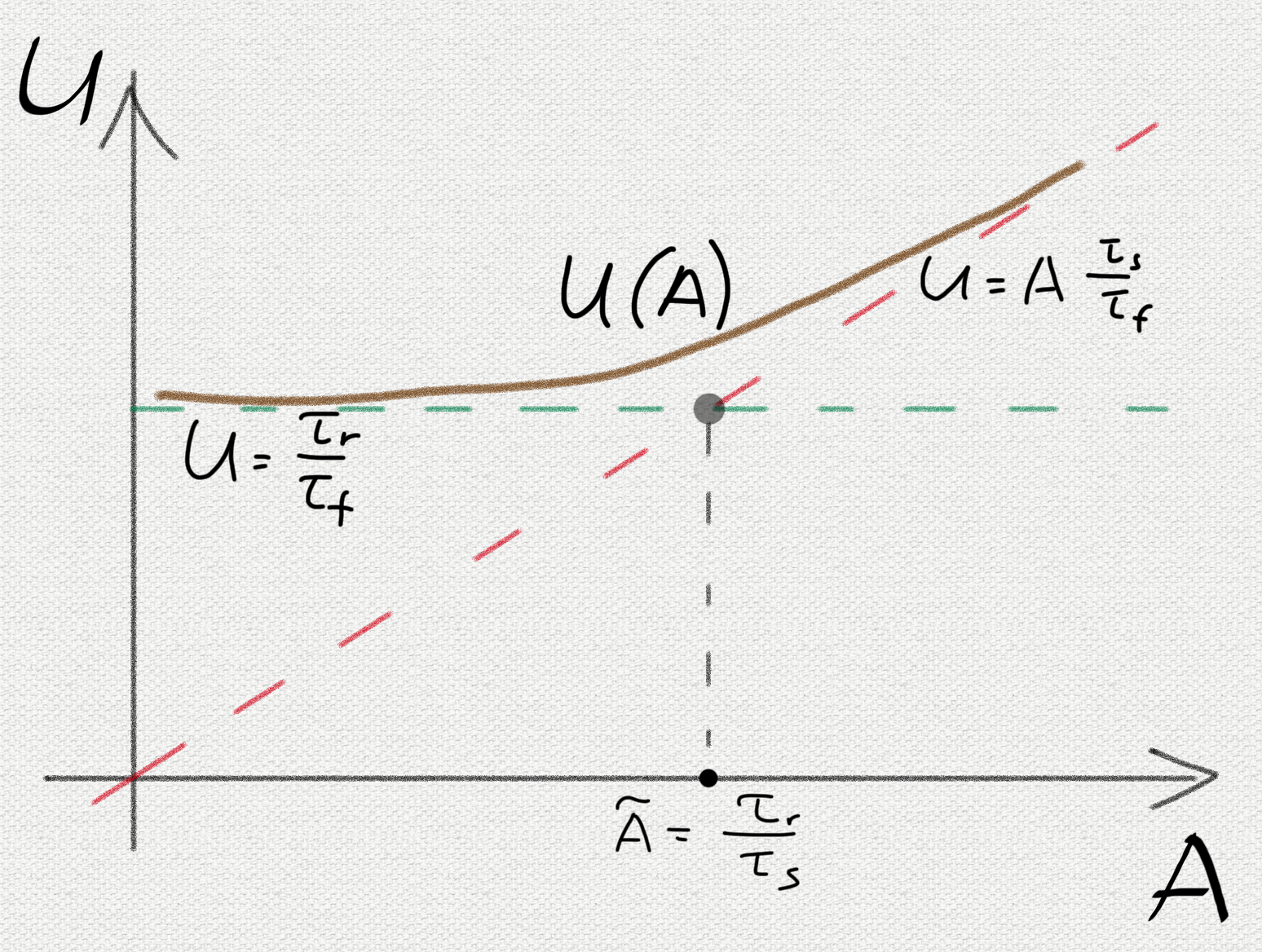
ご覧のとおり、結果は前の結果と一致しますが、要因は例外です 。 2つの制限的なケースを検討してください。

1. 。 この場合、前述のすべての引数が保持されます。チャンクの数はノードの数に依存しないため、クラスターの成長に伴って成長しません。
   
2. 。 この場合 ノードの数が増えると直線的に成長します。
   

モードを決定するために、何が等しいかを評価します 。 -これは、複製されていないチャンクの検出とその複製の計画の特徴的な合計時間です。 概算（「空への指」技術を使用）では、100秒の値が得られます。 次に：


したがって、これらの条件下でこの数値を超えるクラスターがさらに増加すると、チャンクが失われる可能性が高くなります。

状況を改善するために何ができますか？ 境界を動かすことで漸近性を改善できると思われる 増やすことによって ただし、これは値を増やすだけです 実際の改善なし。 最も確実な方法：この削減 、つまり チャンク複製の決定時間 鉄の特性に依存し、ソフトウェアでこれに影響を与えることは困難です。

限界例の議論

提案されたモデルは、実際にクラスターのセットを2つのキャンプに分割します。

ノード数が1000未満の比較的小さなクラスターは、最初のキャンプに隣接していますこの場合、複製されていないチャンクを取得する確率は、次の単純な式で表されます。


状況を改善するには、2つのアプローチを適用できます。

1. 鉄を改善し、それによって増加します 。
   
2. 削減することで複製を高速化 。
   

これらの方法は一般的にかなり明白です。

2番目のキャンプでは、ノード数が1000を超える大規模および超大規模サーバーが既にあります。ここでは、依存関係は次のように決定されます。


つまり は、ノードの数に正比例します。これは、クラスターのその後の増加が、複製不足のチャンクの可能性に悪影響を与えることを意味します。 ただし、ここでは、次のアプローチを使用して、悪影響を大幅に減らすことができます。

1. 増え続ける 。
   
2. 複製不足のチャンクの検出とその後の複製計画を加速し、それにより 。
   

2番目の削減アプローチ もはや明らかではありません。 20秒と100秒の違いは何ですか？ ただし、この値は、複製されていないチャンクの可能性に大きく影響します。 また、自明ではないという事実も 、つまり 複製速度自体は重要ではありません。 このモデルでは理解できます。ノードの数が増えると、この速度は増加するだけであるため、複製の検出と計画を目的とした複製プロセスの「加速」を絶えず追加すると、チャンクの複製に大きな影響を与え始めます。

もう少し滞在する価値があります 。 チャンクの寿命への直接的な貢献に加えて、増加 利用可能なノードの数に対する有益な効果


したがって、使用可能なノードの数が増えます。 したがって、改善 クラスターリソースの可用性に直接影響し、計算を高速化すると同時にデータストレージの信頼性を向上させます。 一方、鉄の品質を改善すると、クラスターの所有コストに直接影響します。 説明したモデルにより、このような決定の経済的実現可能性を定量化できます。

アプローチの比較

結論として、2つのアプローチを比較したいと思います。 これについて雄弁に次のグラフを教えてください。





最初のグラフからは線形の関係しか見ることができませんが、「状況を改善するために何をする必要があるか」という質問には答えられません。2番目の図は、何をすべきか複製プロセスの動作に影響します。 さらに、さまざまなアーキテクチャ上の決定の結果を評価するための、文字通り頭の中の迅速な方法のレシピを提供します。 言い換えれば、開発されたモデルの予測力は質的に異なるレベルにあります。

チャンクの損失

チャンクが失われた特徴的な時間を見つけました。 これを行うために、複製の程度= 3を考慮して、そのようなチャンクの形成プロセスの速度を書き出します。


ここで 2つのコピーが欠落している複製不足のチャンクの数を示します。 -中間状態、類似 状態に対応 、そして 失われたチャンクを意味します。 次に：


どこで -失われたチャンクの形成の特徴的な時間。 次の場合のケースを制限する2つのケースについてシステムを解決します。 。

それから


のために 私達は得る：


つまり 失われたチャンクの形成の特徴的な時間は1億年です！ この場合、ほぼ同様の値が取得されます。 私たちは移行ゾーンにいます。 特性時間の値 自分自身で語り、誰もが自分で結論を出すことができます。

ただし、1つの機能に注意する価値があります。 極端な場合 ながら 定数であり、独立しています の表現で 逆の関係、つまり クラスターの成長に伴い、トリプルレプリケーションはデータのセキュリティを向上させます クラスターがさらに成長すると、状況はまったく逆に変わります。

結論

この記事では、大きなクラスターのプロセスの速度論をモデル化するための革新的な方法を紹介しています。 クラスターダイナミクスを記述するために考慮される近似モデルにより、データ損失を記述する確率的特性を計算できます。

もちろん、このモデルはクラスターで実際に起こっていることの最初の近似にすぎません。 ここでは、定性的な結果を得るための最も重要なプロセスのみを考慮しました。 しかし、そのようなモデルでさえ、クラスター内で何が起こっているかを判断することができ、状況を改善するための推奨事項も提供します。

それにもかかわらず、提案されたアプローチは、さまざまな要因の微妙な説明とクラスターの運用に関する実際のデータの分析に基づいて、より正確で信頼できる結果を可能にします。 以下は、モデル改善の完全なリストからはほど遠いものです。

1. クラスターノードは、さまざまなハードウェア障害のために失敗する可能性があります。 特定のサイトの障害は、通常、異なる確率を持っています。 さらに、たとえばプロセッサの障害は、データを失うことはなく、ノードの一時的な利用不能を与えるだけです。 これは、さまざまな状態を導入することにより、モデルで簡単に考慮されます 、 、 など プロセスの速度と結果がさまざまです。
   
2. すべてのノードが同等に役立つわけではありません。 パーティごとに性質と障害の頻度が異なる場合があります。 これは、モデルで導入することで考慮できます。 、 など 対応するプロセスの異なる速度で。
   
3. さまざまなタイプのノードをモデルに追加します：部分的に破損したディスク、禁止など。たとえば、ラック全体をオフにし、クラスターが定常モードに移行する特徴的な速度を明らかにする効果を詳細に分析できます。 さらに、プロセスの微分方程式を数値的に解くことにより、チャンクとノードのダイナミクスを視覚的に考慮することができます。
   
4. 各ドライブには、待ち時間やスループットなど、わずかに異なる読み取り/書き込み特性があります。 それでも、 Maxwell速度分布で積分されたガスの速度定数との類推により、ディスクの特性の対応する分布関数で積分することにより、プロセスの速度定数をより正確に推定することができます。
   

したがって、動的アプローチでは、一方で、簡単な説明と分析の依存関係を取得できますが、一方で、クラスター操作データの分析に基づいて、必要に応じて特定のポイントを追加して、追加の微妙な要因とプロセスを導入する可能性が非常にあります 結果の方程式に対する各因子の寄与の影響を評価することができ、その便宜を考慮して改善をモデル化することができます。 最も単純な場合、このようなモデルを使用すると、分析の依存関係をすばやく取得して、状況を改善するためのレシピを提供できます。 シミュレーションは本質的に双方向にすることができます。運動方程式系にプロセスを追加することにより、モデルを繰り返し改善することができます。 そして、関連するプロセスをモデルに導入することにより、潜在的なシステム改善の分析を試みます。 つまり コードでのそれらの即時のコストのかかる実装に対する改善のモデリングを実行します。

さらに、特定の影響または小さな摂動に対するシステムのダイナミクスと応答を取得することにより、剛性の非線形微分方程式のシステムを常に数値的に統合することができます。

したがって、一見無関係な知識の領域の相乗効果により、否定できない予測力を持つ驚くべき結果を得ることができます。

YTの開発者、Grigory Demchenko

---