データの視覚化は常に、利用可能なデータを調べるのに役立つ何らかのグラフィカルな構成です。 幾何学的モデルを構築し、それを変更してデータのさまざまな側面を表現します。 また、視覚による制限が課せられています。つまり、視覚化の次元は2つを超えることはできません。 利用可能なすべてのグラフィックツールは2次元です。1枚の紙またはモニター画面です。
一次元データの図を例として使用して、幾何モデルの構築方法、修正方法、およびデータと視覚化の次元がどのように現れるかを見てみましょう。
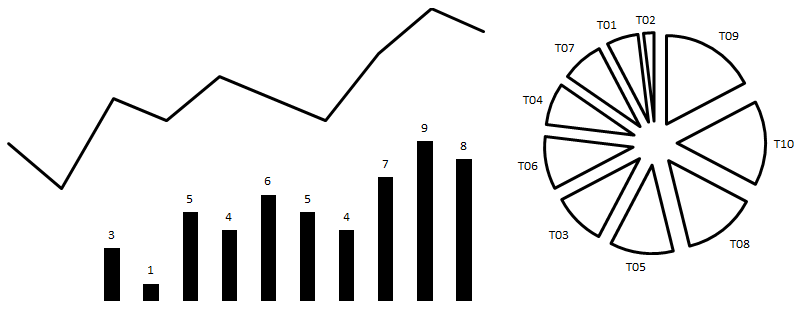
数値の最も単純な幾何モデル
1つの変数の多くの値(速度、温度、価格など)を考慮してください。例:
3、1、5、4、6、5、4、7、9、8
データの1次元性とは、変数が1つしかないことを意味します。 数値シリーズのプロパティを調べるために、幾何モデル、つまりデータ要素(数値)が幾何オブジェクト(ポイント、ライン、円)を使用して表されるモデルを構築します。
数値シリーズの場合、最も単純なのは、長さが数値に比例する各数値に線を割り当てることです。 たとえば、番号3に対応する線は、番号1に対応する線よりも3倍長くなります。結果は通常の棒グラフになります。
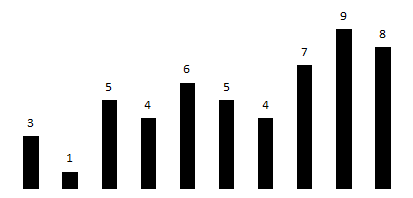
データのさまざまな側面を探索するための視覚化の変換
次に、さまざまな側面を調べるために、数値シリーズの最も単純なモデルを変更します。
棒グラフの重要なパラメーターは、グラフの基点(水平軸)から最上部までの距離です。 この距離は、ある時点での変数の値に比例します。 上位のポイントのみを残してそれらを接続すると、グラフ(折れ線グラフ)が表示されます。 グラフでは、ポイントは時間の順に左から右に並べられています。
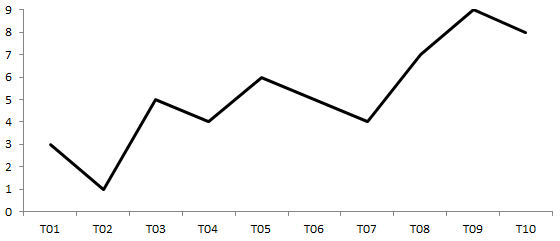
行を時間ではなく、昇順または降順で並べ替えると、棒グラフが表示されます。 このチャートは、評価の提示に非常に適しており、変数の値を(ランクごとに)降順または昇順でソートして視覚化できます。 次に、順序付きリストのようになります。
変換はより複雑になりました。 ソートされた行のセットをグループに分割します。 各グループには、特定の長さの線のみがあり、与えられた境界値以上でありません。 各グループについて、特定の間隔に含まれる行(値)の数を考慮します。 結果の値には新しい行が割り当てられます。 元のラインが死んだかのように、それらを上下に積み重ねます。 次に、間隔の最大(最小)境界の昇順で新しい行を配置し、ヒストグラムを取得します。
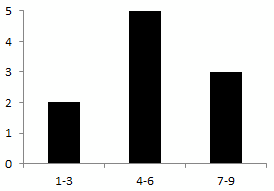
横軸に沿ったヒストグラムは、棒グラフとは対照的に、元の変数の値を示しています。 したがって、棒グラフは、特に同時に使用する場合は特に、ヒストグラムと混同しないように、水平に配置するのが最適です。
視覚的次元削減
上記の図は、1次元のデータが視覚化されているにもかかわらず、2次元であることがわかります。
- グラフ:時間と変数値
- 棒グラフ:変数の値とランク(水平線の向き)
- ヒストグラム:値の間隔と数
つまり、視覚化の次元は、必ずしもデータの次元と一致するとは限りません。
視覚化の次元を効果的に増やすことは困難ですが、次元を減らすことは非常に簡単です。 このような変更により、1つの変数の値を視覚化およびモデル化するための図をさらに取得できるようになります。
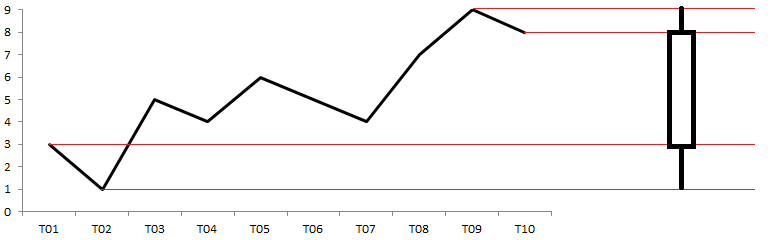
チャートの1次元の類似物は、区間チャートまたはローソク足チャートであり、多くの場合、株価チャートの表示に使用されます。 その構築のために、変数の4つの値(初期、最終、最小、最大)のみを残します。 時間間隔を詳細に調べる代わりに、境界値(時間と大きさ)のみを調べます。 間隔グラフでは、最終値が初期値(成長)よりも大きい場合は四角形は塗りつぶされず、逆方向(ドロップ)の場合は四角形が塗りつぶされます。
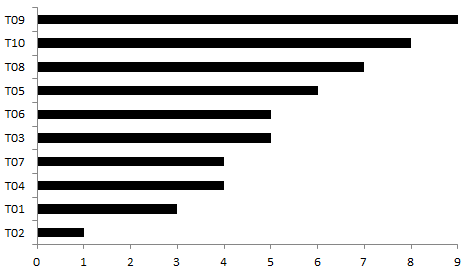
次に、棒グラフを構成するすべての線を取り、それらを直列に接続します。 最大値に対応する最も長い線を使用し、次に大きな線を追加します。 そして、開始点と終了点を閉じて、円を取得します。 したがって、変数に対応する各線は円の弧になり、円自体は整数(すべての値の合計)に対応します。 各値のこのシェアでは、円のセクターとシェアに比例する特定の角度が対応します。
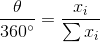
円グラフができました。
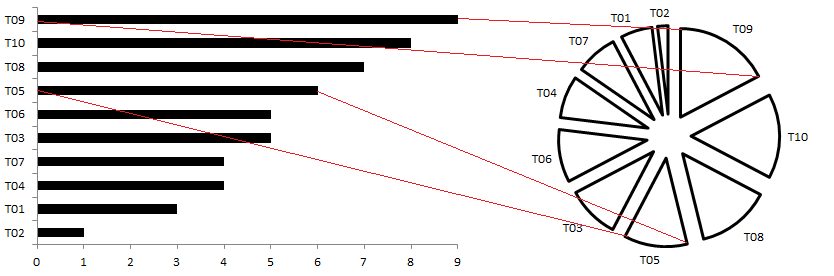
最後に、ヒストグラムの次元を減らします。 間隔グラフと同様に、分布を特徴付けるいくつかの基本的な値、最小値と最大値、2つの四分位数、中央値のみを残します。 四分位が四角形の境界を設定するスケールチャートまたは口ひげのあるボックス(ボックスプロット)を取得し、中央の垂直線が中央値です。
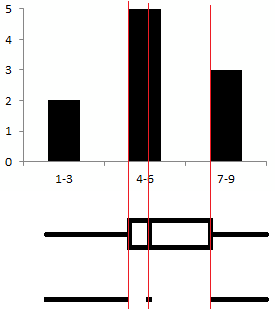
「ミニマリスト」タフティによって提案された下位バージョンは、この視覚化の1次元性を明確に示しています。
間隔グラフ(日本のローソク足)とスパングラフ(口ひげのある箱)は非常に似ています。 したがって、特にそれらを一緒に使用する場合は、キャンドルを垂直に、ボックスを水平に向ける方が適切です。
全体として、圧縮されているかのように低い次元の表現は、いくつかの一連の値が比較される視覚化を構築することを可能にします。
一次元データの視覚化のためのチャート選択
次に、1次元データを視覚化するための図を選択するのに役立つテーブルを作成します。 調べた6つの図は、視覚化の次の側面によって分類されています。
- 時系列(詳細または短い)
- 比率:値と全体に対する値の間
- 間隔での値の分布(詳細かつ簡潔に)
| 寸法 | 時間 | 態度 | 配布 |
|---|
| 2D | グラフ | 棒グラフ | 棒グラフ |
| 1D | 間隔チャート(「和ろうそく」) | 円グラフ | スパンチャート(「口ひげボックス」) |
結論
- 1次元データのチャートは幾何モデルとして提示され、異なるチャート間の関係が考慮されます。
- 幾何モデルの変更(視覚化)により、調査中のデータのさまざまな側面を示すことができます。
- 図の次元を変更すると、たとえば比較のために、より簡潔な形式で情報を表示できます
参照資料