ジェフリー・ブライアント、パコ・ジェイン、マイケル・トロットによる投稿の翻訳、「隠れた数字：軌道および再突入計算への現代的アプローチ」。
記事のコードはここからダウンロードできます。
出版物の翻訳と準備にご協力いただいたPolina Sologubに感謝します。

内容

- 衛星を特定の場所に配置する
- 定数と一次処理
- 計算
- プロット
- 今日の軌道の計算方法は？
衛星シミュレーションを返す

最近映画館で公開された隠された人物は良い評価を受けました。この行動は米国の歴史上重要な時期に行われます。また、公民権や宇宙競争などの多くのトピックにも取り組んでいます。物語の中心にあるのは、水星計画の展開と有人宇宙飛行の初期の研究中のNASAのキャサリンジョンソンと彼女の同僚（ドロシーヴォーンとメアリージャクソン）の物語です。当時のNASAでのアフリカ系アメリカ人女性の劇的な公民権闘争にも注意が向けられています。当時、コンピューターはほとんど登場していなかったため、ジョンソンと同僚がコンピューターを使用せずに軌道力学の複雑な航行問題を解決する能力は、初期のコンピューター結果の重要なテストを提供しました。

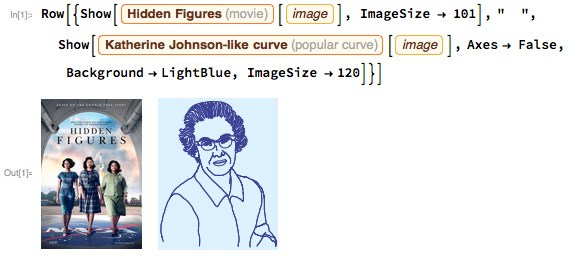
映画で言及されている彼女の科学的研究の2つの側面に焦点を当てます：軌道計算と大気進入に関連する計算です。軌道計算では、最初にジョンソンとまったく同じことを行い、次にWolfram言語ツールを使用して、より現代的な直接アプローチを適用しました。この映画では、オイラー法による微分方程式の解法に言及しています。この方法を最新の方法と比較し、Wolfram言語から直接取得した大気モデルデータを使用してリターンパスを計算します）。

この映画は、ジョンソンチームによる数学的問題の解決の詳細をカバーしていませんが、あなたが見るものは、映画に示されたアプローチを現在存在するアプローチと感じ、比較するのに十分です。

特定の場所に衛星を配置する

ジョンソンが共著（「燃え尽き地点で方位角を決定して選択されたポイントの上に衛星を配置する」）の最初の作品の1つは、特定の軌道の周りの特定の回転数の後、衛星が地球の特定のポイントの上に配置できるかどうかを確認する問題を扱っています開始位置（フロリダ州ケープカナベラルなど）および回転経路。ジョンソンチームがロケットを発射するための方位角（エンジンがオフになったときの宇宙船の速度ベクトルが固定方向で、たとえば北に形成する角度）を決定するために使用したアプローチは、他の軌道パラメーターに基づいていました。これは、宇宙飛行士が地球上の大気圏に入るために正しく配置されることを保証するための重要なステップです。

定数と一次処理

この記事では、Johnsonが問題を手動で解決するために必要ないくつかの定数と入力パラメーターを定義しています。ロケットエンジンの停止を指す「燃え尽き症候群」という用語を説明するために少し脱線します。「燃え尽きた」後、軌道のパラメータはそのまま「凍結」し、宇宙船は地球の重力の影響下でのみ移動します（ニュートンの法則に従って）。このセクションでは、この記事で採用されたユニットの定義に従います。

便宜上、一部の関数は、ラジアンではなく度単位の角度と相互作用するように定義されています。これにより、角度を計算するときに作業を最適化できます。

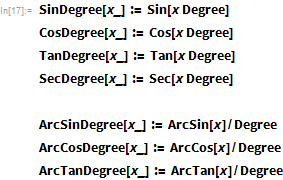
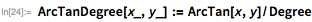
ジョンソンは他のいくつかの派生パラメーターについて説明しますが、興味深いのは、時々特定の値を取り、式を使用して取得した値を使用しないことに注意することです。彼女が採用した値は、式で得られた値に近いことがよくありました。簡単にするため、ここでは式の値を使用しています。

セミラタス直腸楕円軌道：

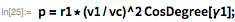
近地点と燃え尽き地点の間の軌道平面の角度：

軌道離心率：

軌道周期：

偏心異常：

次のパラメータを説明するには、元の記事を引用する方が簡単です。「 n軌道を完了した後、バーンアウトポイントφ1、λ1が選択された位置φ2、λ2を通過するという要件は、最初の回転中に、衛星が通過するという要件と同等です選択した位置と同じ緯度φ2の場所。ただし、経度λ2は、完全なn回の回転中に地球の回転を補償するのに十分な量、つまり極からλ2から東にシフトします。 したがって、この同等の位置の経度は、比率 「：

角度θの近地点からの時間：

計算

最終決定の一部は、中間パラメーターδλ1-2 _eおよびθ2 _eの値を決定することです。これにはいくつかの方法があります。まず、 ContourPlotを使用して、記事の式19と20を使用してグラフィカルなソリューションを取得できます。

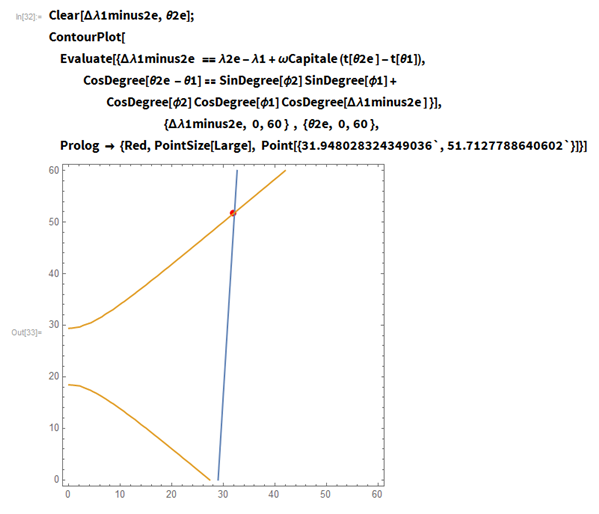FindRootを使用して、数値解を見つけることができます。

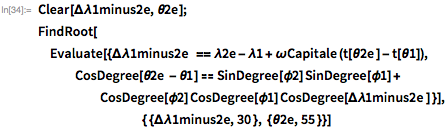
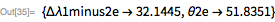
もちろん、JohnsonはContourPlotまたはFindRoot関数にアクセスできなかったため、彼女の記事では反復法について説明しています。この記事で説明した方法論をWolfram言語に翻訳し、反復法を使用して他の多くのパラメーターも開示しました。基本的な計算は地球の球形に対して計算されるため、平坦化の修正が含まれます。

さまざまな反復のθ2eのグラフ表示は、急速な収束を示しています。

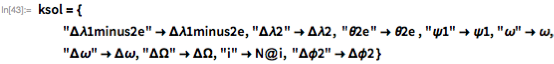
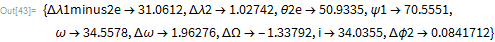FindRootコマンドのメソッドを次のように変換できます。

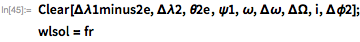
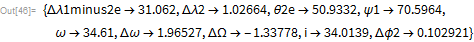
興味深いことに、このより複雑なシステムのルートを見つけるための反復的なステップでさえ、非常に迅速に収束します。

プロット

軌道パラメータが決定されると、解を視覚化できます。まず、以前のソリューションからいくつかのパラメーターを抽出する必要があります。

次に、方位角に応じて、衛星の緯度と経度を取得する必要があります。

φsおよびλs - θsの関数としての緯度と経度：

衛星地上トラックは、ポイントテーブルを作成することで構築できます。

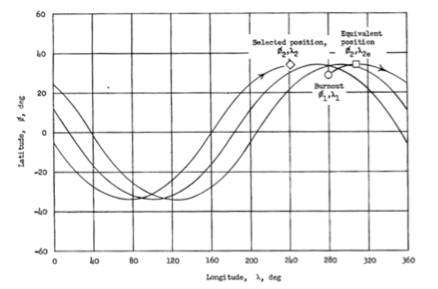
ジョンソンの記事は、燃え尽き症候群を示すマーカーと、選択された同等の位置を含む軌道ソリューションの図を示しています。同様のスキームは簡単に再現できます。

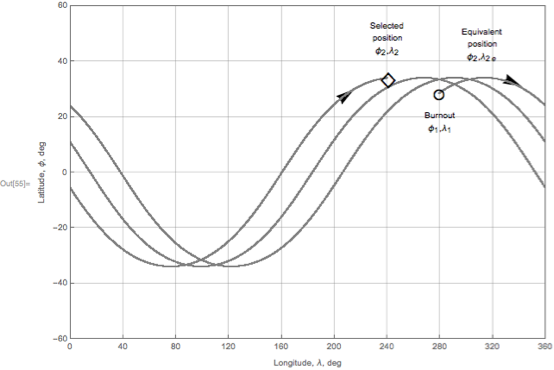
比較のための彼女の元の図は次のとおりです。

地理中心座標を測地線に変換するGeoGraphics関数を使用して、視覚的に便利なバージョンを作成できます。

今日の軌道の計算方法

今日、私たちのほとんど全員が、NASAが1960年代に持っていたものよりもはるかに強力なコンピューティングリソースにアクセスできます。今では、デスクトップコンピューターとWolfram言語のみを使用して、キャサリンジョンソンとそのチームが行ったような軌道力学の問題に対する直接の数値解を簡単に見つけることができます。

より現代的な方法を使用して方位角ψを計算するには、フロリダ上で燃え尽きた後に発生する単純な円形軌道のパラメーターを設定しましょう。また、地球は球対称であると仮定します（ジョンソンの記事のデータとの正確な対応を見つけようとはせず、現代のSI単位系を使用していくつかの量を再定義しようとはしません）。ジョンソンが使用する地球の軌道と同じ高さから開始し、球面三角法を使用すると、軌道の初期条件を簡単に導き出すことができます。

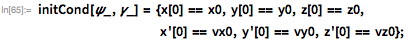
対応する物理パラメーターは、Wolfram言語を使用して直接取得できます。

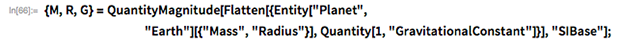
次に、地球の重力場を考慮して、宇宙船の運動の微分方程式を受け取りました。地球の近くの重力ポテンシャルをモデル化する方法はいくつかあります。惑星が球対称で、デカルト座標系を使用すると仮定します。

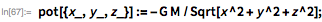
さらに、地球の重力のより現実的なモデルを使用できます。このモデルでは、平らな回転楕円体が惑星の形状として使用されます。このような楕円体のポテンシャルの正確な形状（楕円体シェルの質量密度が一定である場合）は、 EntityValueを使用して利用できます。

一般的な均質な三軸楕円体の場合、ポテンシャルには区分的な関数が含まれます。

ここで、 κは式x ² /（a ² + κ ）+ y ² /（ b ² + k ）+ z ² /（ c ² + κ ）= 1の最大根です。平坦化された楕円体を扱う場合は、式は基本関数に単純化できます...

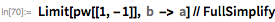
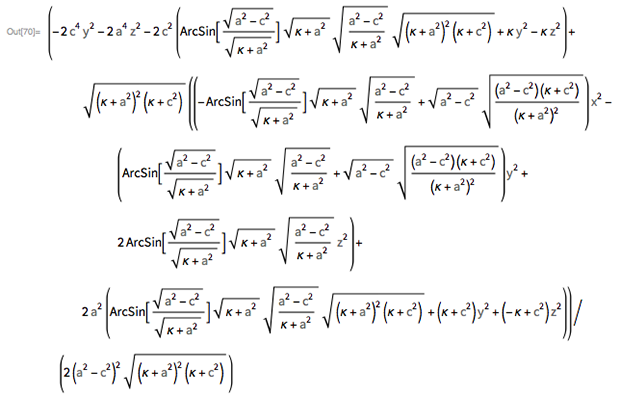
...ここでκ =（（2 z ² （ a ² - c ² + x ² + y ² ）+（- a ² + c ² + x ² + y ² ） ² + z ⁴ ） ^1/2 - a ² - c ² + x ² + y ² + z ² ） / 2。

ここで使用するより単純な形式は、いわゆる一般に受け入れられている重力加速度（IGF）の式によって定義されます。この式は、球面対称ポテンシャルから球面調和関数の2次までの差を考慮し、前述の正確なポテンシャルと数値的に区別できない結果を提供します。測定された4つの測地パラメータに関して、IGFポテンシャルは次のように定義できます。

GeogravityModelData関数を使用すると、重力のより正確な値を簡単に使用できます。初期位置では、IGFポテンシャルは高次近似から0.06％だけ逸脱しています。

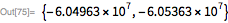
ポテンシャルのこれらの機能的な形態では、軌道経路を見つけるには、重力場ベクトルを取得するためにポテンシャル勾配を計算し、次にニュートンの第三法則を使用する必要があります。 2つの重力モデルの軌道運動方程式を取得します。

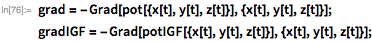
これで、 NDSolveの力を使用して軌道軌道を計算する準備ができました。ただし、これを行う前に、軌道パスを3次元空間で曲線の形で表示すると便利です。これらの曲線をコンテキストに埋め込むために、地球の表面のテクスチャマップ上に作成し、球体に投影しました。ここで、必要なグラフィックオブジェクトを作成しました。

慣性基準フレームで計算された軌道経路は周期的な閉曲線を形成しますが、宇宙船はその後の各回転中に地球の表面のさまざまなポイントを通過することがわかります。 NDSolve関数から取得したソリューションに余分な回転時間を追加することにより、この効果を視覚化できます。軌道周期の数が3（ジョングレンの飛行に似ている）であると仮定すると、Johnsonの記事の研究と同様に、 マニピュレート関数を使用して軌道経路が方位角ψにどのように依存するかを確認しました。球形の地球（白色）と平坦化の効果を示すために緑色のグラフを作成します（ターンごとに差異が増加することに注意してください）。

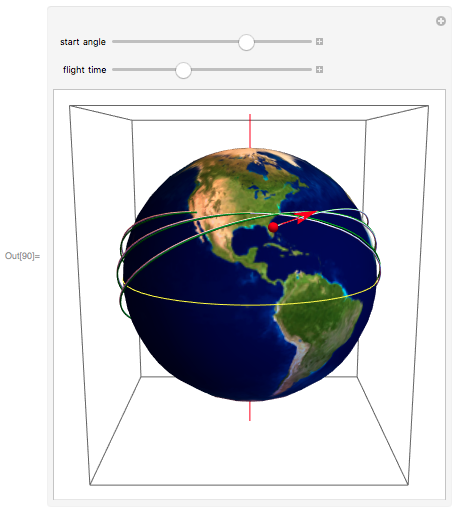
このエントリに付属のドキュメントでは、 操作中のManipulate関数を確認できます。新しいソリューションが配置される速度に注意してください。うまくいけば、キャサリン・ジョンソンとNASAの同僚が感動するでしょう！

現在、バーンアウトポイントで角度ψを変更することにより、たとえば3回転後に宇宙船の位置を簡単に計算できます。

衛星シミュレーションを返す

このフィルムは、リターンフェーズに関連するオイラー法にも言及しています。前のセクションで行ったように、方位角を見つけるという最初の問題を解決した後、地球に戻る時が来ました。回転を遅くするために、ロケットが発射され、その後、宇宙の大気のない環境から大気への移行中に、複雑な一連のイベントが発生します。宇宙飛行士を地球に安全に帰還させるには、大気密度の変化、急速な制動、摩擦加熱などの要因を考慮する必要があります。時間の関数としての高度、速度、加速度の問題を解決する必要があります。この一連の問題は、キャサリンジョンソンが行ったオイラー法を使用して、またはWolfram言語の微分方程式を解く機能を使用して解決できます。

単純な微分方程式の場合、示された求積法を使用して、詳細なステップバイステップのソリューションを取得できます。時間に依存する質量m （t）の有名なニュートンの式F = maに相当するものは、理想的なロケット（1次元）のいわゆる方程式です...

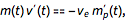
...ここで、 m （t）はロケットの質量、 v _eはロケットエンジンの排気速度、 m ^' _p （t）は燃料質量と時間の微分です。定数m ^' _p （t）の場合 、方程式の構造は比較的単純で、閉じた形で簡単に解くことができます。

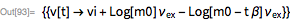
質量の初期条件と最終条件があると、ロケットの運動の有名な方程式が得られます（ K.E. Tsiolkovsky、1903 ）：

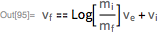
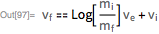
特定のパラメーター値を使用したこの方程式の解の詳細は、 Wolfram | Alphaから取得できます。これらは、正確な解と他の数値積分法との比較とともに詳細です。

映画のプロットに続いて、私は現在、再入国プロセスのミニマリストモデルを実装しています。グレンの飛行を模倣するパラメーターを定義することから始めましょう。

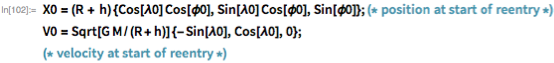
ブレーキング中は、第1段階のエンジン推力の1％が使用され、60秒間続くと思います。運動方程式：

ここで、 F _gravは重力、 F _exhaust （ t ）は時間に依存するモーターの力、摩擦力F _Friction （ x （ t ）、 v （ t ））です。後者は、位置x （ t ）の空気密度とv （ t ）の摩擦の法則の両方に依存します。

高さに依存する空気密度の場合、 StandardAtmosphereData関数を使用できます。地上約8.5 kmの高度で開くパラシュートのため、私も考慮に入れています。

これにより、解く必要のある次の連成非線形微分方程式が得られます。 WhenEvent関数[...]は、カプセルが地球の表面に到達したときに、リモートコントロールソリューションの構築の終わりを指します。変数XとVの位置と速度のベクトル値を使用します。

重量、排気ガス、空気摩擦のこれらの定義を考えると、視点...

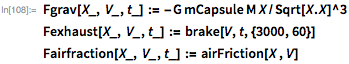
...結果として生じる力は、次のようにして見つけることができます。

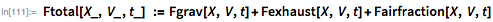
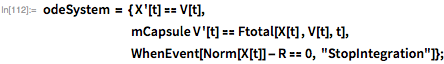
このモデルでは、地球の回転、カプセルの内部回転角、飛行角のアクティブな変化、摩擦の超音速効果などを無視しました。キャサリン・ジョンソンが解く方程式：

この方程式系は、初期位置と速度で補足される場合、単に数値的に解かれます。これを行うには、 NDSolve関数を使用します。 Wolfram言語は重要な結果を保証する値を自動的に選択するので、使用する方法、ステップサイズ制御、エラー制御などについて心配する必要はありません：

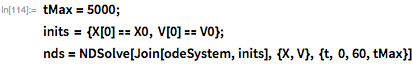
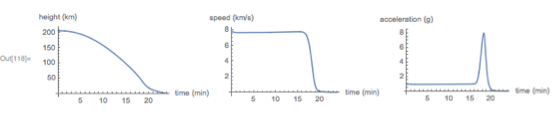
これは、高度、速度、加速度対時間のグラフです。

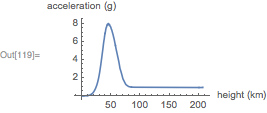
高さ対時間の曲線は、空気密度の指数関数的な増加が強いブレーキングの原因であることを示しています。これは、比較的低い高度で発生するパラシュートによるものではありません。カプセルが真空から大気にすばやく移動するとき、減速ピークは非常に高い高度で発生します。

また、再入力時のカプセルの垂直および接線速度のグラフを次に示します。

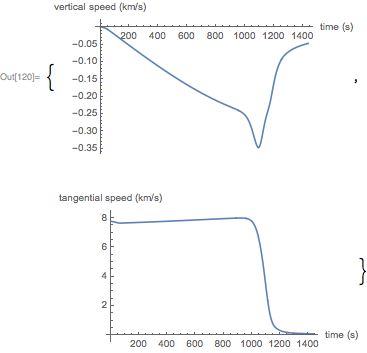
次に、固定ステップでオイラー法を使用した数値解法を繰り返します。

定性的には、このソリューションは前のソリューションと同じように見えます。

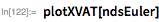
経時的な積分ステップの使用サイズについては、累積誤差は数パーセントのオーダーです。ステップサイズを小さくすると、エラーが減少します。

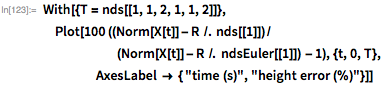
オイラー法によって予測された着陸時間は、前の時間と比較してわずか0.11％だけずれていることに注意してください（比較のために、2つの最新の方法、たとえば「BDF」または「Adams」で方程式を解いた場合、エラーは数桁少なくなります）。

再入力プロセスでは大量の熱が発生します。ここには熱シールドが必要です。単位面積あたりの最大熱量Qはどの高さで生成されますか？詳細に入ることなく、純粋に次元上の理由から、仮説を適用することができます