
みなさんこんにちは! アルゴリズムの武器を補充する時が来ました。
今日、私たちは最も人気があり実践されている機械学習アルゴリズムの1つである勾配ブースティングを徹底的に分析します。 ブースティングのルーツがどこから来て、アルゴリズムの裏で実際に何が起こっているのかについて-カットの下でブースティングの世界への私たちのカラフルな旅で。
UPD:現在、コースは英語で、 mlcourse.aiというブランド名で、Medium に関する記事 、Kaggle( Dataset )およびGitHubに関する資料があります 。
オープンコースの2回目の立ち上げ(2017年9月から11月)の一環として、この記事に基づいた講義のビデオ 。
この記事の概要:
- 紹介と歴史の向上
- GBMアルゴリズム
- 損失関数
- GBM理論の要約
- 宿題
- 便利なリンク
1.ブースティングの紹介と歴史
データ分析に関与するほとんどの人は、少なくとも1回はブーストを行うことを聞いています。 このアルゴリズムは、次のタスクで試してみる価値のあるモデルの「紳士用セット」に含まれています。 Xgboostは、多くの場合、 MLコンペティションに勝つための標準的なレシピに関連付けられており、「スタックxgboosts」に関するミームを生み出しています。 そしてブースティングはほとんどの検索エンジンの重要な部分です。 一般的な開発について、ブースティングがどのように現れて発展したかを見てみましょう。
ブースティングストーリー
すべては、多数の比較的弱く単純なモデルから1つの強いモデルを取得できるかどうかという問題から始まりました。 弱いモデルとは、ニューラルネットワークなどのより「強い」モデルとは対照的に、意思決定ツリーのような小さく単純なモデルだけではありません。 私たちの場合、弱いモデルは任意の機械学習アルゴリズムであり、その精度はランダムな推測よりもわずかに高い場合があります。
この質問に対する肯定的な数学的答えは非常に迅速に見つかりました。それ自体が重要な理論的結果でした(MLの希少性)。 ただし、実行可能なアルゴリズムとAdaboostが登場するまでに数年かかりました。 彼らの一般的なアプローチは、入力データを重み付けすることにより、単純なモデルの線形結合(基本アルゴリズム)を熱心に構築することでした。 後続の各モデル(原則として決定木)は、以前に誤って予測された観測値に大きな重みと優先度を与えるような方法で構築されました。
Adaboostについてもう少し良い方法で、機械学習に関する残りのほとんどのコースの例に従い、勾配ブースティングの前に、その前身であるAdaboostを注意深く調べてください。 ただし、AdaboostはGBMとの合併を経て、これが単なるプライベートなバリエーションであることが明らかになったため、すぐに最も興味深いものに進むことにしました。
アルゴリズム自体は、背後にある観測値を計量する直感を非常に明確に視覚的に解釈しています。 Adaboostの各反復でデータを深さ1のツリー(いわゆる「切り株」)で除算しようとする分類問題のおもちゃの例を考えてみましょう。 最初の2回の繰り返しで、次の図が表示されます。
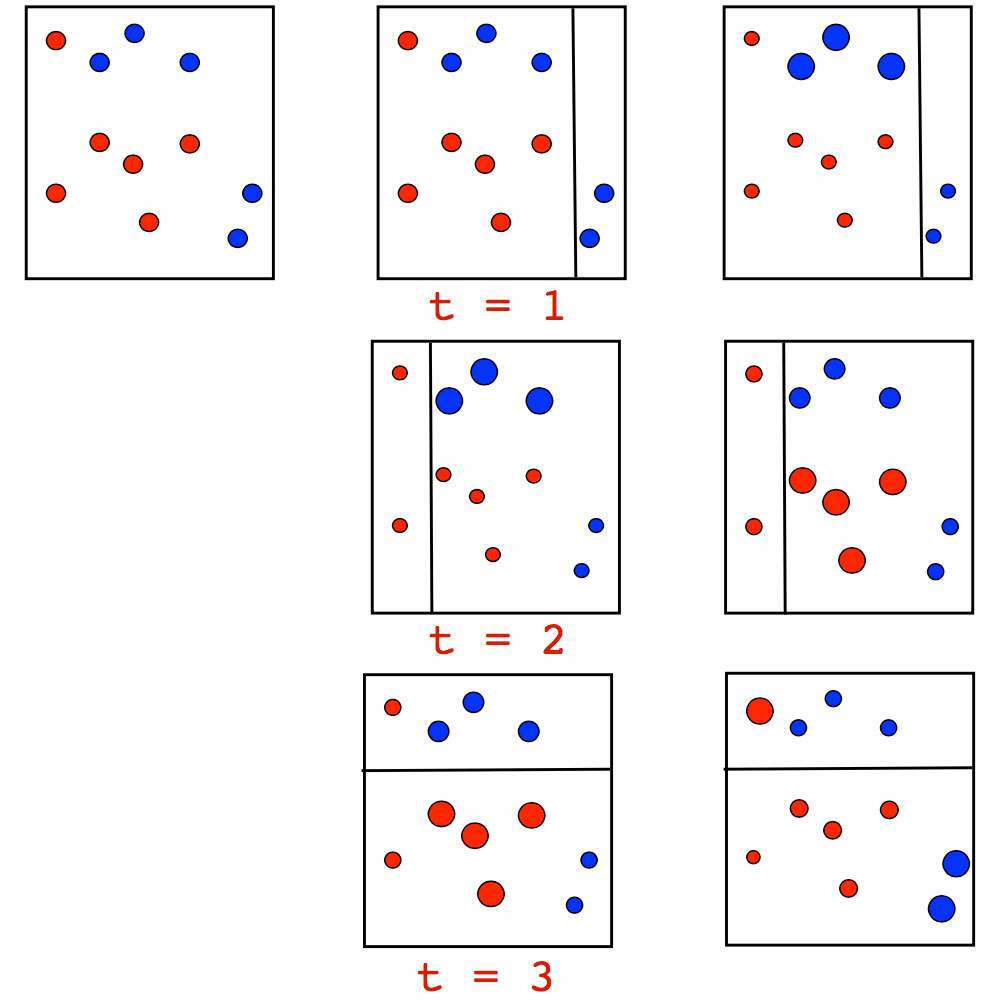
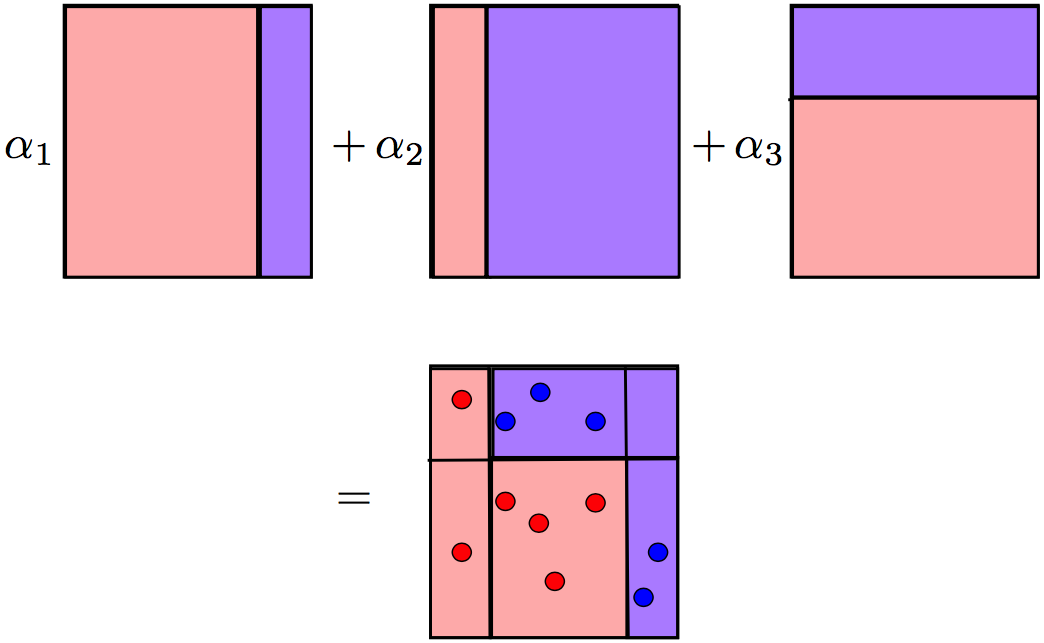
ポイントのサイズは、誤った予測で受け取る重みに対応します。 そして、各反復で、これらの重みがどのように増加するかを確認します-切り株はそのようなタスクだけでは対処できません。 ただし、以前に構築された切り株の加重投票を行うと、目的の分離が得られます。
Adaboostの動作のより詳細な例。一連の反復中に、特にクラス間の境界で、ポイントが順次増加することが示されています。
Adaboostはうまく機能しましたが、アドオンで動作するアルゴリズムの正当性がほとんどなかったため、さまざまな推測がそれらの周囲に発生しました:誰かがそれを超アルゴリズムと魔法の弾丸と見なし、誰かが懐疑的であり、この意見を共有しましたタイトなオーバーフィッティングによるほとんど適用できないアプローチ。 これは、Adaboostが不安定であることが判明した高排出データへの適用性に特に当てはまりました。 幸いなことに、すでにラッソ、エラスティックネット、ランダムフォレストの世界をもたらしたスタンフォード統計学部の教授がビジネスを始めたとき、1999年にジェロームフリードマンは、ブースティングアルゴリズム(勾配ブースティング、別名Gradient Boosting(Machine)、別名GBM)の成果の一般化を思い付きました。 この作業により、フリードマンはすぐに多くのアルゴリズムを作成するための統計的基礎を設定し、機能空間で最適化としてブーストするための一般的なアプローチを提供しました。
スタンフォードレガシー一般的に、スタンフォード統計局のチームは、CART、ブートストラップ、その他多くのことに関与しており、将来の統計教科書に名前を事前に入力しています。 概して、私たちの日常的なツールの大部分がそこに登場し、誰が他に何が現れるかを知っています。 または、すでに登場していますが、まだ十分な配布が見つかりません( glinternetなど)。
フリードマン自身のビデオはあまりありません。 しかし、彼と一緒に、CARTの作成に関する非常に興味深いインタビューがあります。一般に、40年以上前の統計的問題(データとデータサイエンスの分析に起因する)の解決方法について:
データ分析の有益な歴史のシリーズから、あなたが使用する私たちの毎日の方法を作成する参加者の1人からのデータ分析の回顧と、 Hastieからの講義もあります:
実際、アルゴリズムの構築におけるエンジニアリングおよびアルゴリズムの研究(MLの特徴)から、そのようなアルゴリズムの構築および研究方法の本格的な方法論への移行がありました。 数学的スタッフィングの観点から見ると、一見したところそれほど大きな変化はありません:弱いアルゴリズムを追加(ブースト)し、以前のモデルがファイナライズされていないデータの部分を徐々に改善してアンサンブルを構築します。 しかし、次の単純なモデルを構築するとき、それはオーバーウエイトされた観測だけでなく、目的関数の一般的な勾配をより良く近似するような方法で構築されます。 概念レベルでは、これは想像力と拡張の大きな範囲を与えました。
GBMの歴史
勾配ブースティングは、すぐに「紳士のセット」に置き換わることはありませんでした-登場してから10年以上かかりました。 まず、ベースGBMには、さまざまな統計タスク用の多くの拡張機能があります。既存のGAMモデルを強化するGLMboostとGAMboost、生存曲線用のCoxBoost、ランキング用のRankBoostとLambdaMARTです。 第二に、異なる名前と異なるプラットフォームで同じGBMの多くの実装があります:確率的GBM、GBDT(勾配ブースト決定木)、GBRT(勾配ブースト回帰ツリー)、MART(多重加法回帰ツリー)、一般ブースティングマシンとしてのGBMその他。 さらに、機械学習者のコミュニティは非常に細分化されており、すべてに従事していました。このため、ブースティングの成功を追跡することは非常に困難です。
同時に、ブースティングは検索エンジン結果のタスクのランキングに積極的に使用され始めました。 この問題は、損失関数の観点から書き出されたものであり、発行順序のエラーに罰金を科すため、GBMに単純に挿入するのが便利になりました。 AltaVistaはランキングのブーストを導入した最初の企業の1つであり、すぐにYahoo、Yandex、Bingなどが続きました。 さらに、実装について言えば、今後数年間ブーストすることが作業エンジン内の主要なアルゴリズムになり、いくつかの科学記事に含まれる別の交換可能な研究技術ではなくなったと言われました。
 ブースティングを普及させる主な役割は、ML競技、特にkaggleが果たしました。 研究者は、十分な参加者とタスクがあり、アルゴリズムとアプローチを備えた人々が最先端のオープンな闘争で競争するための共通のプラットフォームを長い間欠いていました。 ガレージで別の奇跡のアルゴリズムを成長させた陰鬱なドイツの天才は、もはや閉じられたデータに帰することができず、逆に真のブレークスルーライブラリは、開発のための優れたプラットフォームを受け取りました。 これはまさにブーストで起こったことであり、ほぼすぐにkaggleに定着しました (2011年以降、勝者とのインタビューでGBMを探す必要があります)。ライブラリとしてのxgboostは、登場後すぐに人気を博しました。 同時に、xgboostは新しいユニークなアルゴリズムではなく、追加のヒューリスティックを備えた古典的なGBMの非常に効率的な実装です。
ブースティングを普及させる主な役割は、ML競技、特にkaggleが果たしました。 研究者は、十分な参加者とタスクがあり、アルゴリズムとアプローチを備えた人々が最先端のオープンな闘争で競争するための共通のプラットフォームを長い間欠いていました。 ガレージで別の奇跡のアルゴリズムを成長させた陰鬱なドイツの天才は、もはや閉じられたデータに帰することができず、逆に真のブレークスルーライブラリは、開発のための優れたプラットフォームを受け取りました。 これはまさにブーストで起こったことであり、ほぼすぐにkaggleに定着しました (2011年以降、勝者とのインタビューでGBMを探す必要があります)。ライブラリとしてのxgboostは、登場後すぐに人気を博しました。 同時に、xgboostは新しいユニークなアルゴリズムではなく、追加のヒューリスティックを備えた古典的なGBMの非常に効率的な実装です。
そして、2017年に、数学的問題やアルゴリズム技術からMLの非常に典型的な方法で、通常のアルゴリズムと通常の方法論の出現から成功した実用的なアプリケーションとその出現後の大量使用に至るアルゴリズムを使用しています。
2. GBMアルゴリズム
ML問題のステートメント
教師による指導という一般的な文脈で、機能を回復する問題を解決します。 機能ペアのセットがあります \大x およびターゲット変数 \大Y 、 \大\左\ {(x_i、y_i)\右\} _ {i = 1、\ ldots、n}\大\左\ {(x_i、y_i)\右\} _ {i = 1、\ ldots、n} 、フォームの依存関係を復元します \大y = f ( x ) 。 近似により復元します \大\帽子F ( X ) 、どの近似がより良いかを理解するために、損失関数もあります \大L ( y 、 f ) これを最小化します:
\大Y \約\ハットF ( X )、\大\ハットf(x)=\アンダーセットf(x) arg min L(y、f(x))
これまでのところ、中毒の種類については何も仮定していません。 \大f(x) 、近似のモデルについてではありません \大\帽子f(x) 、またターゲット変数の分布について \大y 。 それは機能ですか \大L(y、f) 微分可能でなければなりません。 世界のすべてのデータで問題を解決するのではなく、自由に使えるデータでのみ解決する必要があるため、期待の点ですべてを書き換えます。 つまり、近似値を探します \大\帽子f(x) そのため、平均で次のデータの損失関数を最小化できます。
large hatf(x)= undersetf(x) arg min mathbbEx、y[L(y、f(x))]
申し訳ありませんが、機能 \大f(x) 世界にたくさんあるだけではありません-それらの非常に機能的な空間は無限です。 したがって、何らかの方法で問題を解決するために、機械学習では、検索空間は通常、特定のパラメーター化された関数ファミリーに制限されます largef(x、 theta)、 theta in mathbbRd 。 これにより、パラメータ値のすでに完全に解決可能な最適化に減少するため、問題が大幅に簡素化されます。
large hatf(x)=f(x、 hat theta)、 large hat theta= underset theta arg min mathbbEx、y[L(y、f(x、\シータ))]
最適なパラメーターの分析ソリューション \大\帽子\シータ 1行に存在することはほとんどないため、通常、パラメーターは反復的に近似されます。 まず、経験的損失関数を書き出す必要があります LargeL theta( hat theta) データに基づいてそれらをどの程度適切に評価したかを示します。 近似値も書きます \大\帽子\シータ のために \大M 和の形式での反復(明確にするため、およびブーストに慣れるため):
large hat theta= sumMi=1 hat thetai、 largeL theta( hat theta)= sumNi=1L(yi、f(xi、 hat theta))
ポイントは小さいです-最小化する適切な反復アルゴリズムを使用するだけです LargeL theta( hat theta) 。 最も簡単で最も頻繁に使用されるオプションは、勾配降下です。 そのためには、グラデーションを書く必要があります large nablaL theta( hat theta) 繰り返し評価を追加します \大\帽子 thetai それに沿って(マイナス記号付き-エラーを減らし、増加させたくない)。 それだけです。最初のアプローチを何らかの方法で初期化するだけです。 \大\帽子 theta0 そして、反復回数を選択します \大M この手順を続けます。 メモリーを使用しない形式での近似値の保存 \大\帽子\シータ 単純なアルゴリズムは次のようになります。
- 初期パラメーター近似の初期化 large hat theta= hat theta0
- 反復ごとに \大t=1、\ドット、M 繰り返します:
- 損失関数の勾配を計算する large nablaL theta( hat theta) 現在の近似値で \大\帽子\シータ
large nablaL theta( hat theta)= left[ frac partialL(y、f(x、 theta)) partial theta right] theta= hat theta - 現在の反復近似を設定する \大\帽子 thetat 計算された勾配に基づいて
\大\帽子 thetat\左矢印− nablaL theta( hat theta) - パラメータ近似の更新 \大\帽子\シータ :
large hat theta leftarrow hat theta+ hat thetat= sumti=0 hat thetai
- 最終近似を保存 \大\帽子\シータ
large hat theta= sumMi=0 hat thetai - 見つかった機能を使用する \大きい hatf(x)=f(x、 hat theta) 予約制
機能勾配降下
意識を広げる:機能空間で最適化を実行し、近似を繰り返し検索できることを少し想像してください \大\帽子f(x) 関数自体の形で。 近似は、それぞれが関数である漸進的な改善の合計として書きます。 便宜上、最初の近似から始めて、この量をすぐに考慮します \大\帽子f0(x) :
large hatf(x)= sumMi=0 hatfi(x)
マジックはまだ起こっていません、私たちは私たちのアプローチを探すことにしました \大\帽子f(x) 多数のパラメーターを持つ1つの大きなモデル(ニューラルネットワークなど)ではなく、関数の合計の形で、このように機能空間を移動するふりをします。
この問題を解決するには、検索をいくつかの関数ファミリーに限定する必要があります large hatf(x)=h(x、 theta) 。 しかし、最初に、モデルの合計はこのファミリーのどのモデルよりも複雑になる可能性があります(深さ1の2つの木の切り株の合計は1つの切り株でもはや近似できません)。 第二に、一般的なタスクは機能空間でまだ行われています。 関数の各ステップで最適な係数を選択する必要があることをすぐに考慮します \大 rho in mathbbR 。 ステップ用 \大t タスクは次のとおりです。
large hatf(x)= sumt−1i=0 hatfi(x)、 large( rhot、 thetat)= underset rho、 theta arg min mathbbEx、y[L(y、 hatf(x)+ rho cdoth(x、 theta))]、 large hatft(x)= rhot cdoth(x、 thetat)
そして今が魔法の時です。 私たちはすべてのタスクを一般的な方法で書きました。まるで好きなモデルを取り、訓練できるかのようです。 \大きいh(x、 theta) 損失関数に関して \大きいL(y、f(x、 theta)) 。 実際には、これは非常に困難であるため、問題を解決中のものに減らす簡単な方法が考案されました。
損失関数の勾配の表現がわかれば、データでその値を計算できます。 それでは、予測がこの勾配と最も相関するようにモデルをトレーニングしましょう(マイナス記号付き)。 つまり、OLS回帰の問題を解決し、これらの残差の予測をまっすぐにしようとします。 そして分類のため、そして回帰のため、そして内部のランキングのために、私たちは常に疑似残基間の差の二乗を最小化します \大r そして私たちの予測。 ステップ用 \大t 最終タスクは次のとおりです。
large hatf(x)= sumt−1i=0 hatfi(x)、 largerit=− left[ frac\部分L(yi、f(xi))\部分f(xi)\右]f(x)= hatf(x)、 quad mboxfori=1、 ldots、n、 large thetat= underset theta arg min sumni=1(rit−h(xi、 theta))2、 large rhot= underset rho arg min sumni=1L(yi、 hatf(xi)+ rho cdoth(xi、 thetat))
フリードマンの古典的なGBMアルゴリズム
1999年にJerome Friedmanによって提案されたGBMアルゴリズムを最終的に書き出すために必要なものはすべて揃っています。 私たちは今でも、教師と教えるという一般的な問題を解決しています。 アルゴリズムの入力時に、いくつかのコンポーネントを収集する必要があります。
- データセット \大\左\ {(x_i、y_i)\右\} _ {i = 1、\ ldots、n} ;
- 反復回数 \大M ;
- 損失関数の選択 \大L(y、f) 描かれたグラデーションで;
- 基本的なアルゴリズムの機能ファミリーの選択 \大きいh(x、 theta) 、彼らのトレーニングの手順;
- 追加のハイパーパラメーター \大きいh(x、 theta) たとえば、決定木のツリーの深さ。
放置された唯一の瞬間は、最初のアプローチでした \大きいf0(x) 。 簡単にするために、定数値のみが初期化として使用されます \大\ガンマ 。 彼と同様に最適な比率 \大 rho バイナリ検索、または(勾配ではなく)元の損失関数に関連する別のライン検索アルゴリズムを見つけます。 したがって、GBMアルゴリズム:
- 定数値でGBMを初期化する large hatf(x)= hatf0、 hatf0= gamma、 gamma in mathbbR
large hatf0= underset gamma arg min sumni=1L(yi、 gamma) - 反復ごとに \大t=1、\ドット、M 繰り返します:
- 擬似残り物を数える \大きいrt
largerit=− left[ frac partialL(yi、f(xi)) partialf(xi) right]f(x)= hatf(x)、 quad mboxfori=1、 ldots、n - 新しい基本アルゴリズムを構築する \大きいht(x) 擬似残骸の回帰のような \大\左\ {(x_i、r_ {it})\右\} _ {i = 1、\ ldots、n}
- 最適な比率を見つける \大 rhot で \大きいht(x) 元の損失関数と比較して
large rhot= underset rho arg min sumni=1L(yi、 hatf(xi)+ rho cdoth(xi、 theta)) - 保存する \大\帽子ft(x)= rhot cdotht(x)
- 現在のアプローチを更新 \大\帽子f(x)
large hatf(x) leftarrow hatf(x)+ hatft(x)= sumti=0 hatfi(x)
- 最終的なGBMモデルを構築する \大\帽子f(x)
large hatf(x)= sumMi=0 hatfi(x) - 訓練されたモデルでkaggleと世界を征服する(そこで予測を立て、自分でそれを理解する)
GBMのステップバイステップの例
おもちゃの例を使用して、GBMの仕組みを理解してみましょう。 ノイズの多い関数を復元するために使用します largey=cos(x)+ epsilon、 epsilon sim mathcalN(0、 frac15)、x in[−5,5] 。
これは実際のターゲット変数での回帰のタスクであるため、二乗平均平方根損失関数を使用します。 300組の観測値を自分で生成し、それらを深さ2の決定木で近似します。GBMを使用するために必要なすべてをまとめましょう。
- 玩具データ \大\左\ {(x_i、y_i)\右\} _ {i = 1、\ ldots、300} ✓
- 反復回数 \大M=3 ✓;
- RMS損失関数 \大L(y、f)=(y−f)2 ✓
勾配 \大きいL(y、f)=L2 損失は残り物です \大r=(y−f) ✓; - 基本的なアルゴリズムとしての決定木 \大h(x) ✓;
- 決定木のハイパーパラメーター:木の深さは2✓です。
二乗平均誤差は単純であり、初期化されています \大\ガンマ および係数付き \大 rhot 。 つまり、平均値でGBMを初期化します large gamma= frac1n cdot sumni=1yi そしてすべて \大 rhot 1に等しい
GBMを起動し、2種類のグラフを描画します:実際の近似 \大\帽子f(x) (青いグラフ)、および構築された各ツリー \大\帽子ft(x) 擬似バランス(緑色のグラフ)について。 グラフ番号は反復番号に対応します。
2回目の反復で、ツリーが関数のメインフォームを繰り返したことに注意してください。 ただし、最初の反復では、アルゴリズムが関数の「左ブランチ」のみを構築したことがわかります( \大x in[−5、−4] ) 私たちのツリーにはすぐに対称ブランチを構築するのに十分な深さがなく、左ブランチのエラーが大きかったため、これはひどく起こりました。 , "" .
: - , GBM . , , GBM , . , GBM , Brilliantly wrong :
http://arogozhnikov.imtqy.com/2016/06/24/gradient_boosting_explained.html3.
, , , , ? , y L(y,f) 。 , , .
, — . : y∈R y∈{−1,1} 。 , , , .
y∈R 。 , , (y|x) . :
- L(y,f)=(y−f)2 , L2 loss, Gaussian loss. , . () — .
- L(y,f)=|y−f| , L1 loss, Laplacian loss. , , , . , , , , , .
- , Lq loss, Quantile loss. , , L1 , 75%-, α=0.75 。 , , .
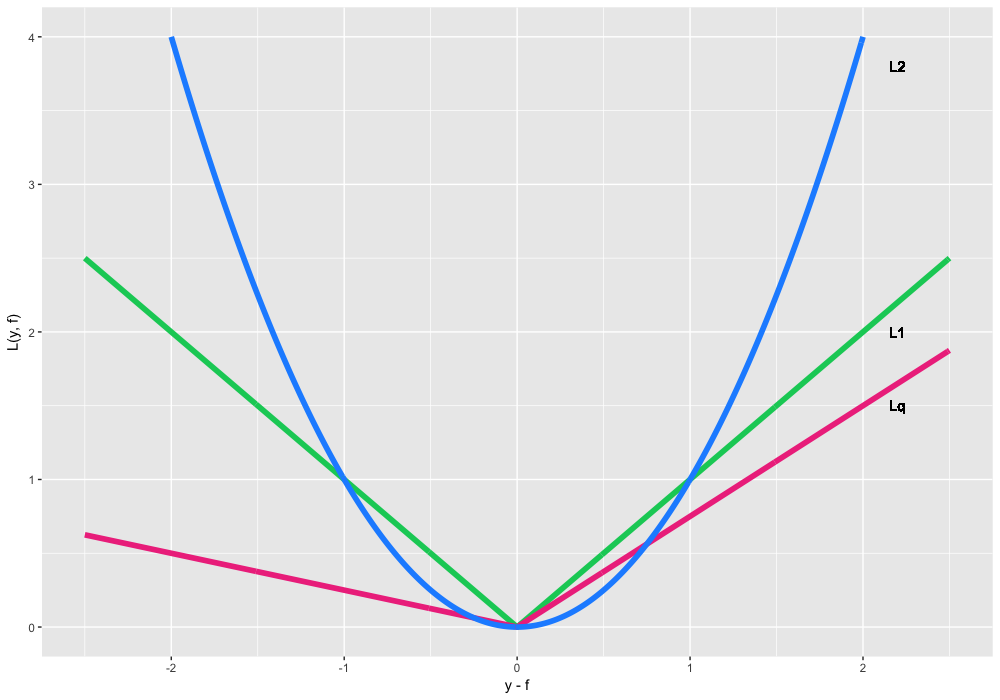
Lq , 75%- . :
- {(xi,yi)}i=1,…,300 ✓
- M=3 ✓;
- ✓;
- L0.75(y,f) — , α=0.75 。 -, :
ri=−[∂L(yi,f(xi))∂f(xi)]f(x)=ˆf(x)=
=αI(yi>ˆf(xi))−(1−α)I(yi≤ˆf(xi)),for i=1,…,300 ✓; - h(x) ✓;
- : 2 ✓;
— y 。 , ρt , line search. , :
実際には、通常のレムナントとは非常に異なる何かをトレーニングしていることを見るのは珍しいです-各反復で \大ri 可能な値は2つだけです。 ただし、GBMの結果は元の関数と非常に似ています。
このおもちゃの例から学習するためにアルゴリズムを離れると、次のようにシフトされた2次損失関数とほぼ同じ結果が得られます。 \大\約0.135 。 しかし、90%を超える分位数を探していると、計算が困難になる可能性があります。 つまり、必要な分位数を超えるポイント数の比率が小さすぎる場合(不均衡なクラスなど)、モデルは定性的に学習できません。 非定型のタスクを解決するときは、このようなニュアンスを考慮する価値があります。
回帰損失関数についてもう少し回帰問題のために、追加のロバストネスプロパティを持つ関数を含む多くの損失関数が開発されました。 そのような例の1つが、フーバー損失関数です。 関数の本質は、わずかな偏差では次のように機能することです \大規模なL2 、所定のしきい値から、次のように機能し始めます \大L1 。 これにより、小さな不正確さと偏差に焦点を合わせずに、関数の一般的な形式への異常値とそれに続く二次的に大きな誤差の寄与を減らすことができます。
次のおもちゃの例で、この損失関数の動作を確認できます。 基礎として、おもちゃのデータ関数を使用します largey= fracsin(x)x 特別なノイズが追加されました。一方向放出ジェネレーターとして機能するガウス分布とベルヌーイ分布の混合。 損失関数自体はADプロットに表示され、対応するGBMはFHプロットに表示されます(Eプロットには初期関数)。
そして、
大きな解像度で 。
この例では、視覚的な明瞭さのための基本的なアルゴリズムとしてスプラインが使用されました。 結局のところ、私たちはすでにあなたが木だけでなく解放できると言っていますか?
例の結果によると、人為的に作成されたノイズの問題により、 \大規模なL2 、 \大L 1 そして、フーバー損失は非常に顕著です。 フーバー損失パラメーターを適切に選択すると、オプションの中から関数の最適な近似を取得することさえできます。 また、この例では、条件付き分位数の違いがはっきりと見えます(この場合は10%、50%、90%)。
残念なことに、フーバー損失関数はすべての最新のライブラリに実装されていません(まだxgboostではなくh2oに実装されています)。 条件付き分位数や条件付きエクスプロイトなどのエキゾチックなものを含む、他の興味深い損失関数にも同じことが当てはまります 。 しかし、一般的に、そのようなオプションが存在し、使用できることを知ることは非常に便利です。
分類損失関数
次に、バイナリ分類を分析します。 \大きいy \ in \左\ {-1、1 \右\} 。 GBMを使用すると、非常に微分不可能な損失関数であっても最適化することができることを既に見ました。 一般に、ためらうことなく、このケースをいくつかの別の回帰問題として解決しようとすることができます \大規模なL2 損失ですが、あまり正確ではありません(可能ですが)。
ターゲット変数の分布は根本的に異なるため、クラスラベル自体ではなく、対数尤度を予測および最適化します。 これを行うために、乗算された予測と真のラベル上の損失関数を再定式化します \大y cdotf (理由がないわけではなく、異なる文字のラベルを選択しました)。 そのような損失の分類関数の最も有名なバリアント:
- \大L(y、f)=log(1+exp(−2yf)) 、彼女はロジスティック損失であり、彼女はベルヌーイ損失です。 興味深い特性は、クラスラベルを正確に予測することさえできたことです。 いいえ、これはバグではありません。 それどころか、この損失関数を最適化することにより、すべての観測値が正しく予測された場合でも、クラスを「押しのけ」、分類器を改善し続けることができます。 これは、バイナリ分類で最も標準的で一般的に使用される損失関数です。
- \大きいL(y、f)=exp(−yf) 、それはAdaboostの損失です。 そのため、従来のAdaboostアルゴリズムは、この損失関数を備えたGBMと同等です。 概念的には、この損失関数はロジスティック損失に非常に似ていますが、分類エラーに対する指数ペナルティがより厳しく、あまり使用されません。
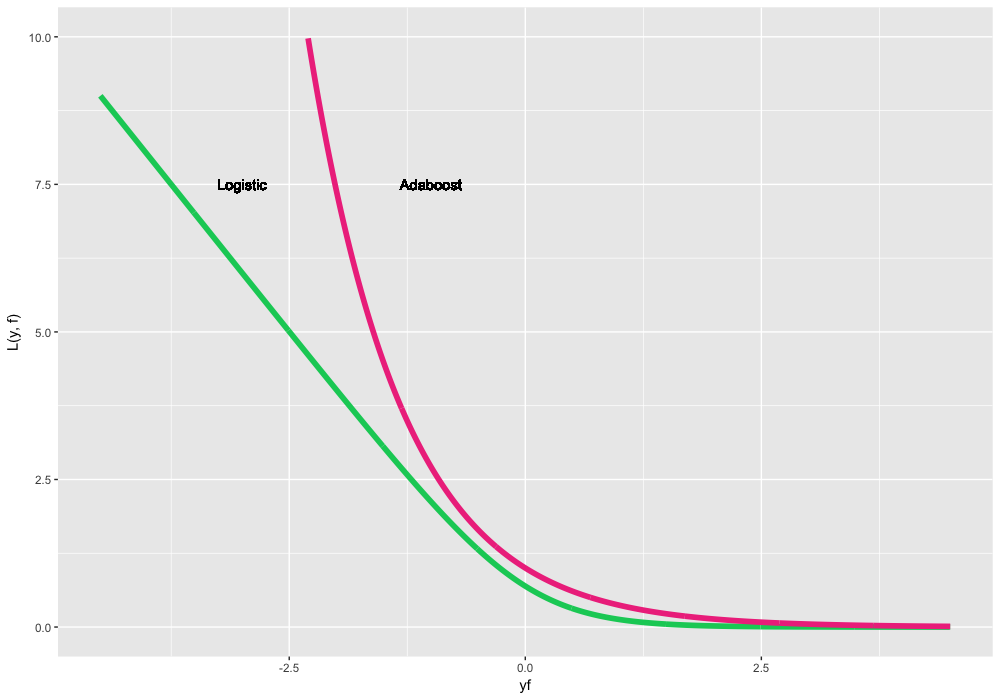
分類問題の新しいおもちゃデータを生成します。 ノイズの多いコサインを基礎として、ターゲット変数のクラスとして符号関数を使用します。 新しいデータは次のとおりです(明確にするためにジッタノイズが追加されています)。
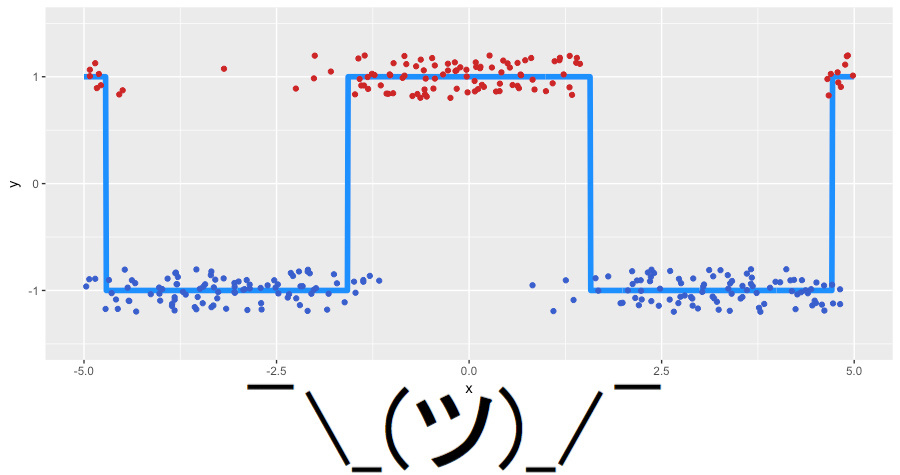
ロジスティック損失を使用して、実際にブーストするものを確認します。 前と同様に、決定するものをまとめます。
- 玩具データ \大\左\ {(x_i、y_i)\右\} _ {i = 1、\ ldots、300}、y_i \ in \左\ {-1、1 \右\} ✓
- 反復回数 \大M=3 ✓;
- 損失関数として-ロジスティック損失、その勾配は次のように考慮されます:
largeri= frac2 cdotyi1+exp(2 cdotyi cdot hatf(xi))、 quad mboxfori=1、 ldots、300ド ✓; - 基本的なアルゴリズムとしての決定木 \大h(x) ✓;
- 決定木のハイパーパラメーター:木の深さは2✓です。
今回はアルゴリズムの初期化で、すべてが少し複雑になります。 まず、私たちのクラスは不均衡であり、約63%から37%の割合で分割されています。 第二に、損失関数の初期化の分析式は不明です。 だから我々は見ていきます \大\帽子f0=\ガンマ 検索:
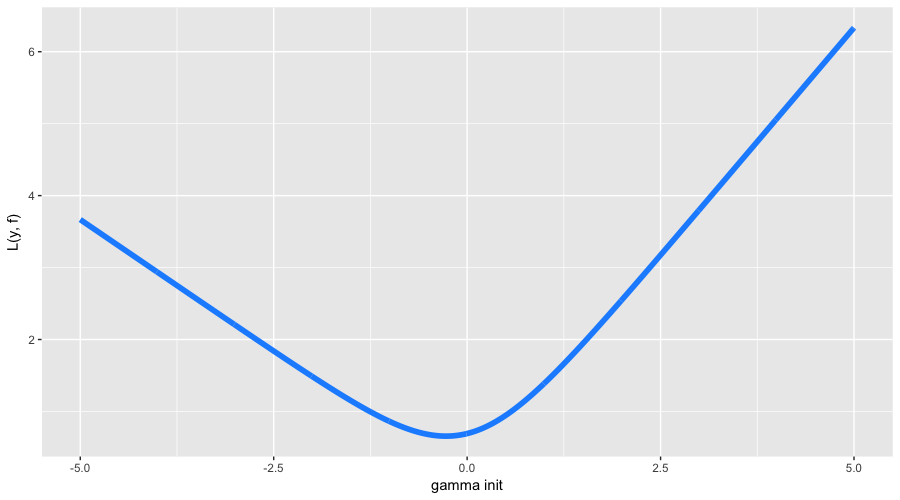
最適な初期近似は-0.273の領域で見つかりました。 負の値になると推測できますが(最も人気のあるすべてのクラスを予測する方が有益です)、正確な値の公式は、すでに述べたようにそうではありません。 さて、最後にGBMを起動して、実際に何が起こるかを見てみましょう。
アルゴリズムは正常に機能し、クラスの分離を復元しました。 「下位」領域がどのように分離されているか、ツリーがネガティブクラスの正しい予測に自信を持っていること、およびクラスが混合された場所で2つのステップがどのように形成されるかを確認できます。 擬似残基から、かなり多くの正しく分類された観測値と、データのノイズに起因する大きな誤差を伴う一定数の観測値があることがわかります。 GBMが分類問題で実際に予測するもののように見えます(ロジスティック損失関数の擬似残差の回帰)。
重さ
タスクに対して、より具体的な損失関数を考え出すときに状況が発生することがあります。 たとえば、金融シリーズの予測では、時系列の大きな動きに大きな重みを付けたい場合があります。また、クライアントの流出を予測するタスクでは、LTVの高いクライアントからの流出(寿命の価値、クライアントが将来私たちにもたらすお金の量)を予測する方が適切です。
統計戦士の本当の方法は、独自の損失関数を考え出し、それに対する導関数を書き(そして、より効果的な訓練のために、ヘッセ行列も)、この関数が必要な特性を満たしているかどうかを注意深くチェックすることです。 しかし、どこかで間違いを犯し、計算上の困難に陥り、一般に研究に容認できないほど長い時間を費やす可能性が高い。
代わりに、非常にシンプルなツールが発明されました。これは実際にはほとんど覚えられていません-観測値の重み付けと重み関数の割り当てです。 このような重み付けの最も簡単な例は、クラスのバランスをとるために重みを設定することです。 一般的な場合、入力変数のようにデータのサブセットがわかっている場合 \大 およびターゲット変数 \大y 私たちのモデルにとって非常に重要です。 \大w(x、y) 。 主なことは、スケールの合理性に関する一般的な要件を満たすことです。
largewi in mathbbR、 largewi geq0 quad mboxfori=1、 ldots、n、 large sumni=1wi>0
重みは、損失関数自体を解決する問題に合わせて微調整する時間を大幅に短縮し、モデルのターゲットプロパティを使用した実験を促進できます。 これらの重みをどのように正確に設定するかは、専ら創造的なタスクです。 GBMアルゴリズムと最適化の観点から、単純にスカラーウェイトを追加し、その性質に目をつぶってください。
largeLw(y、f)=w cdotL(y、f)、 largerit=−wi cdot left[ frac partialL(yi、f(xi)) partialf(xi) right]f(x)= hatf(x)、 quad mboxfori=1、 ldots、n
任意の重みの場合、モデルの美しい統計特性がわからないことは明らかです。 一般に、重みを値に関連付ける \大y 、膝を撃つことができます。 たとえば、比例重みの使用 \大|y| で \大L1 損失関数-同等ではない \大規模なL2 勾配は予測自体の値を考慮しないため、損失 \大\帽子f(x) 。
私たちの能力をよりよく理解するために、これらすべてについて議論しています。 おもちゃデータの重みの非常にエキゾチックな例を考えてみましょう。 強く非対称な重み関数を次のように定義します。
$$ display $$ \ large \ begin {equation} w(x)= \ left \ {\ begin {array} {@ {} ll @ {}} 0.1、&\ text {if} \ x \ leq 0 \\ 0.1 + | cos(x)|、&\ text {if} \ x> 0 \ end {array} \ right。 \ end {equation} $$表示$$
そのような重みの助けを借りて、2つのプロパティが表示されることが期待されます。 \大 、および関数の形式。元のコサインにより類似しています。 最適係数のラインサーチを含む、分類の前の例から取得した他のすべてのGBM設定。 私たちが得たものを見てみましょう:
結果は期待したものです。 最初に、最初の反復で、元のコサインをほぼ繰り返す、異なる疑似残基がどれだけあるかを確認できます。 第二に、関数グラフの左側は、重みが大きい右側を優先してほとんど無視されました。 第三に、3回目の反復で受け取った関数は多くの詳細を受け取り、元のコサインにさらに似たものになりました(また、簡単な再適合を開始することにより)。
重みは、私たち自身の危険とリスクを冒して、モデルのプロパティを大幅に制御できる強力なツールです。 損失関数を最適化する場合は、最初に単純な問題を解決することを試みますが、必要に応じて観測値の重みを追加します。
4. GBM理論の要約
今日は、勾配ブースティングの基本理論について説明しました。 GBMは特定のアルゴリズムではなく、モデルのアンサンブルを構築する方法に関する一般的な方法論です。 さらに、この方法論は非常に柔軟で拡張可能です。さまざまな損失関数を考慮に入れながら多数のモデルをトレーニングし、同時にそれらにさまざまな重み関数をかけることができます。
機械学習の競争の実践と経験が示すように、標準タスク(非常にスパースなデータだけでなく、写真とオーディオを除くすべて)で、GBMはほとんどの場合最も効率的なアルゴリズムです(GBMはほとんど常にスタックと上位レベルのアンサンブルを除きます)それらの不可欠な部分です)。 強化学習 (Minecraft、ICML 2016)にはGBMの適応があり、コンピュータービジョンでまだ使用されているViola-JonesアルゴリズムはAdaboostに基づいています。
この記事では、GBMの正則化、確率論、および関連するアルゴリズムのハイパーパラメーターに関連する質問を特に省略しました。 私たちがいたるところにアルゴリズムの少数の反復を選んだのは理由がないわけではありません。 \大M = 3 。 3つではなく30本のツリーを選択し、上記のようにGBMを実行した場合、結果はあまり予測できません。
このような状況で何をすべきか、GBM正則化パラメーターが相互にどのように相互接続されているか、および基本アルゴリズムのハイパーパラメーターについては、次の記事で説明します。 その中で、最新のパッケージ-xgboost 、 lightgbmおよびh2oを分析し、適切な構成を実践します。 それまでの間、GBM設定を別の非常にクールなインタラクティブデモでプレイすることをお勧めします。
http://arogozhnikov.imtqy.com/2016/07/05/gradient_boosting_playground.html5.宿題
実際の宿題は、コースの次のセッションで発表されます。VKグループとコースリポジトリでフォローできます 。
練習として、 このタスクを完了します -フライト遅延を予測するために、 Kaggle Inclass コンペティションの単純なベースラインを破る必要があります。
6.便利なリンク
貴重なコメントを寄せてくれたyorko (ユリ・カシニツキー)と、編集を手伝ってくれたbauchgefuehl (Anastasia Manokhina)に感謝します。