暗号化と暗号化入門、パート2。 Yandexでの講義

Vladimir ivlad Ivanovの暗号理論の最も短い紹介に戻ります。 これは講義の後半です。数日前に公開した最初の部分です。 彼女にgithubでプルクエストを送信することもできます 。


カットの下-デコードとスライドの一部。

---

-実際の状況は次のとおりです。256ビット長の乱数の2つのサンプル間の衝突は、約40億のサンプルで½の確率に達します。 したがって、64ビットのランダムビットの長さを持つブロックのストリームを考えると、2 ^32個のそのようなブロックの中で確率が½の場合、2つの同一のブロックがあります。

示された科学的事実にはどのような応用価値がありますか？ 暗号化関数の出力は乱数と見なすことができ、理想的な暗号化関数は乱数と区別できません。 したがって、たとえばDESアルゴリズムまたはGOST-28147で暗号化されたブロックを考慮し^、これらのブロック^のうち2 ³²個を使用すると、2つのブロックが同じように暗号化される確率が½になります。

誰かに数えてみましょう：64ビットまたは8バイトの2 ³²ブロック-何個？ 32ギガバイト？ 真実のように聞こえます。 次に、32ギガバイトを10ギガバイトに分割します。 64ビットブロックの暗号化アルゴリズムを使用している場合、少し遅れて32秒後に衝突が発生します。 同じように暗号化された2つのブロックが表示されます。 SHSで見られるように、これらの2つのブロックは同じ平文である必要はありません。 クリアテキストは異なる場合があります。

それはどういう意味ですか？ ブロックC _iがある場合、SHSモードで暗号化されたものは何ですか？

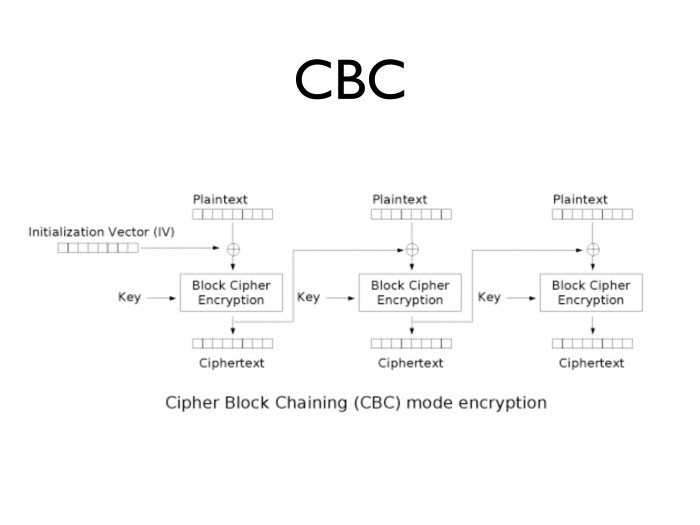
30秒後に衝突が観測されたとします。 2つの部分は等しいです。 暗号化は1対1の対応です。 したがって、暗号化関数は等しいため、暗号化も等しくなります。

C _j-1とC _i-1-通信チャネルで送信されたばかりであるため、それらを見ました。

言い換えれば、ブロックサイズが非常に小さい場合、完全に強力な暗号化を使用していても、しばらくすると、2つのランダムなプレーンテキストの違いを受け取り始めます。 このプロパティは必ずしも実際の攻撃に変換されるわけではありませんが、実際にはあまり良くありません。 そのため、SHS体制は多くのトラブルの原因です。

これらのトラブルの最後は、ほんの数週間前に公開された攻撃（聞き取れない-約編）です。 極端ですが、このシリーズの最後ではないと思います。 すべては、私が話したSHSの不幸な性質のためです。

ただし、SHSは依然として広く普及している暗号化モードです。 どこでも彼に会えます。

-最後の10ビットを取得する必要がある場合、順番にカウントする必要があります...

-はい、もちろん、SHSには問題があります。1ギガバイトを復号化してその中の最後の10バイトを読み取るには、最初にすべてを生成する必要があります。

SHSのすべての難しさにもかかわらず、それは依然として最も一般的な暗号化モードです。確かにTLSですが、IPsecで、つまり、実際に使用されるプロトコルであると思います。

実生活でこれに対処するには？ まず、Triple DESはもはや広く使用されていません。 さらに、128ビットのブロックサイズのAESを見ると、約2 ⁶⁴ブロック後に衝突確率½が発生し、これは大量のトラフィックです。 したがって、実際の生活では、衝突時につまずく可能性は高くありません。 政府機関ではなく、使用を強制されていない場合は、Triple DESとGOST-28147を使用しないでください。

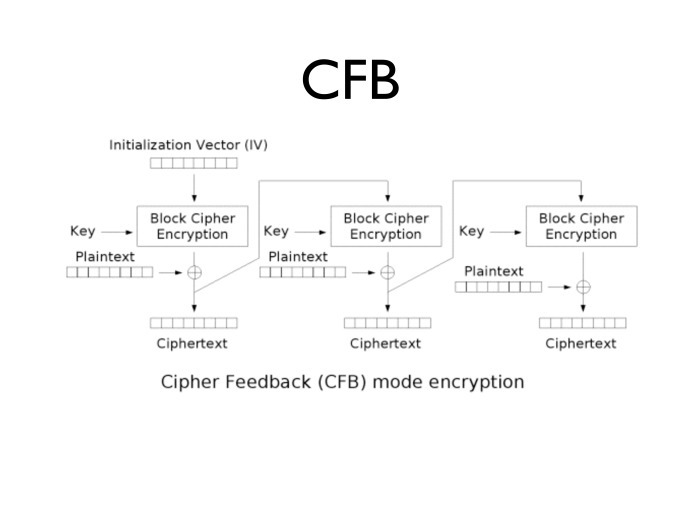
暗号化モードはSHSだけではありません。 まだCFBがあります。 注意深く見れば、彼はSHSと大差ありません。 初期化ベクトルを取得し、それとプレーンテキストをXORし、暗号文を取得します。 結果はもう一度暗号化され、Xorimはプレーンテキストで、テキストの2番目のブロックなどを取得します。

CFBについて話したのはなぜですか？ SHSとは異なり、CFBバリアントは州の標準仕様向けに標準化されているためです。 よく見ると、この意味ではSHSに勝るものはありません。同じ問題があります。 クローズドシステムでは、示された実装に遭遇する可能性があります;原則として、いくつかの問題が発生します。

これらのアルゴリズムには他にどのような問題がありますか？ 後続の各ブロックを復号化するには、暗号化されたプレーンテキストが必要です。 利用可能なプレーンテキストブロックがないと、次の暗号化ブロックを生成できません。 この問題を取り除くために、次のように機能するOFBモードを考え出しました：初期化されたベクトルが与えられ、キーで暗号化され、結果は再びキーで暗号化されます...実際、初期化ベクトルを何度も取得し、必要な数のブロックを暗号化します。

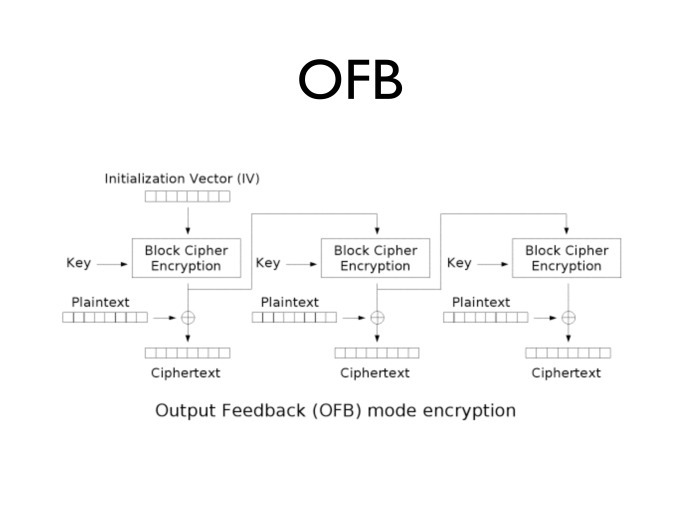
ブロックをクリアテキストで追加します。 なぜこれが便利なのですか？ よく見ると、暗号化のブロックモードはストリーミングに変わります。 現在トラフィックがほとんどなく、プロセッサが空いている場合、事前にいくつかのブロックを生成し、トラフィックが急増する可能性がある場合はそれらを使用できます。 とても快適です。 そして、次のブロックを暗号化するのに平文の知識は必要ありません。 必要に応じて、数ギガバイトのメモリを入力して保持できます。

ストリーム暗号のすべての欠点もここにあります。

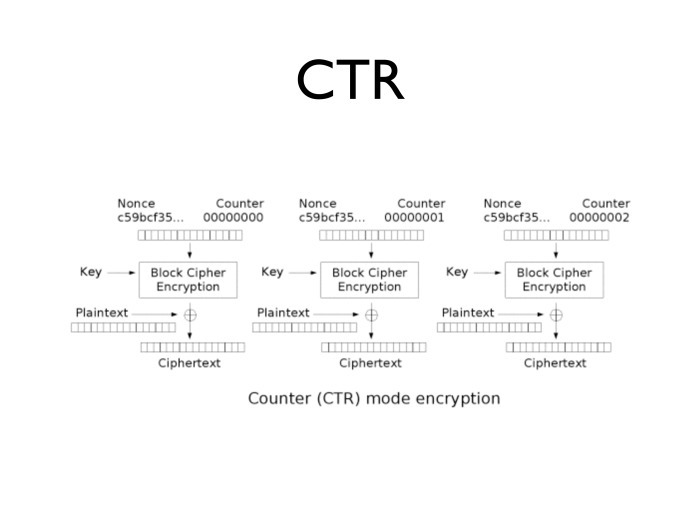
わずかに異なる暗号化方式は、いわゆるカウンターモードまたはCTRです。 構造は単純です。特定の乱数を取得してブロックの先頭に配置し、最後にカウンターを0から必要な数だけ配置します。 たとえば、最大64ビット。 半分に分割します。左の64ビットは乱数に、右の64ビットはカウンターに使用されます。

このような各番号を暗号化し、結果をクリアテキストで削減します。

CTRが便利な理由 これにより、前の124ブロックを暗号化せずに125番目のブロックを暗号化できます。つまり、10ギガバイトのファイルから最後の16バイトを復号化する問題を解決します。 他のすべての意味で非常に便利です。 トラフィックの急増について話す場合、暗号化のためのブロックを事前に生成できます。

これは、1ブロックよりも長いメッセージの場合です。 しかし、それらが1ブロックより短い場合はどうでしょうか？ つまり、16バイトではなく8バイトを暗号化します。

-16まで終了します。

-そして、どうやって？ 末尾に4つのゼロがあるブロックを解読したと仮定します。 これらの4つのゼロがブロックされており、ブロックの断片ではないことをどのようにして知ることができますか？

-暗号化されたメッセージを送信する前に、長さをバイト単位で通知します。

-便利な方法ですが、転送前にサイズを常に把握しているとは限らないという点で不便です。 メールの場合-ご存知ですが、そうでない場合は？

転送後？ さて、おそらくあなたはできます。 そして、違いを探す場所はどこにありますか？ 別の場所で保管する必要があります。 問題はどれですか？

-暗号化のフレームワーク内ではありません。

-暗号化の一部としてメッセージの長さを送信しない場合、それを開示します。 私たちは彼女を隠したと思います。

私の地獄、つまりパディングのあるシステムへようこそ。 メッセージの最後にどれだけの長さを書く必要があるかという考えは、それほど悪くはありません。 ブロックを補完する方法を考え出すことだけが重要です。これにより、データの一部ではなく、最後の部分が追加であることを明確に確認できます。

パディングにはいくつかのモードがありますが、残念ながら、最も一般的なものにはいくつかの不快な特性があります。

最後のブロックの最後に、各空きバイトに空きバイト数を追加します。 最後に3バイトがある場合、それらを取得して書き込みます：3、3、3。

メッセージの長さが境界線上に正確に収まる場合、別のブロックを追加します。私の意見では、4つのゼロを書き込みます。 基本的にではありません。 このコーディング方法は常に一意です。 開いて最後のバイトを認識し、ゼロでない場合、いくつかのバイトをカウントする必要があることを理解します。 実際、これは巧妙にコーディングされたメッセージ長です。 最後のバイトがゼロの場合、ブロック全体を破棄できます。 そして、完全なブロックがゼロで終わることは決してないことを知っています：それから、別の完全にゼロのブロックでそれを補います。

最後のブロックがユニットで終了する場合、それは完全であり、別のブロックで確実に補完します。

それは正常に見えるでしょう。 私たちの前にパディングの動作メカニズムがあります。

攻撃を実行したとしましょう。 Oracleシステムがあります。これは暗号化と呼ばれています。 これは、データベースを作成するOracleの種類ではありません。 これはデバイスがわからないボックスですが、この場合は暗号化または復号化アルゴリズムです。 どのキーが内部にあるかはわかりませんが、何らかの答えが得られます。 ただし、挿入した行が正しくデコードされたのか、誤ってデコードされたのかについて、彼は確かに答えをくれません。

だから、ボックスが示されています。 同時に、1つのメッセージが表示され、そのメッセージが正常に解読されたことを確認できます。 奇妙なことに、実際のシステムでは、このようなメッセージは簡単に受信できます。

次に、メッセージを受け取ってボックスに送信し、最後の1バイトを変更します。 ボックスは2つの状態を返すことができます。 設計が何らかの形でうまく復号化されたこと、またはパディングエラーのために復号化されなかったことを学習します。

どのように機能しますか？ プログラムコードは何かを解読しようとし、それを解読し、最後にパディングをチェックします。 パディングが標準を満たしていない場合は、「333」または何かが間違っています。最後のブロック全体がゼロではなく、「パディングエラー」と表示されます。 このようなスキームにより、最後のブロックの最後のバイトを非常に簡単にソートできます。 たとえば、SHSの不運なモードを使用する場合、プレーンテキストを調べて、ここに何があるかを理解できます。

すべてがかなり無害に見えます。 しかし実際には、パディングオラクル攻撃の問題により、たとえば2008年頃のWindows 2003での悪意のあるコードのリモート実行が発生しました。

なぜこれが起こっているのですか？ 何かを期待しているメッセージが実際にメッセージを送信したことを確認せずに、何かを解読しようとしています。

認証へようこそ。 先ほどお話しした内容はすべて、メッセージの機密性を保証しました。 暗号化を使用して、メッセージを送信し、受信者以外の誰もそれを読み取らないようにします。 しかし、受信者がメッセージを受信したときに、メッセージが実際に送信者から来たことをどのように確認できますか？ この検証のために、メッセージ認証プロトコルの別個のセットがあります。 英語では、これはMAC-メッセージ認証コードと呼ばれます。

問題は何ですか？ ストリーム暗号化アルゴリズムに問題があります。 何も知らないメッセージがあるとします。 何らかの方法で生成されるガンマがあります。 暗号文が判明しました。 暗号が完全に強力であり、すべてがうまくいっているとします。 しかし、攻撃者が受け取ったメッセージの一部を取り込んで変更したとします。 間違いを見つけますか？ 明らかにそうではありません。

彼がゼロビットを1に変更した場合、彼は予想外に平文を変更しました。 暗号文でユニットをゼロに変更し、元のメッセージでこの場所にもゼロがあった場合、それは1に変更されます。 暗号文を少し「反転」すると、平文も反転します。 また、この問題は単一の暗号化アルゴリズムでは検出できません。

ブロック暗号にはさらに問題があり、それらが蓄積し、おそらくパディングの問題に遭遇することは明らかですが、一般にこの問題は依然として存在します。 暗号化だけではメッセージ認証は提供されません。 別のメカニズムが必要です。

このメカニズムはMASと呼ばれます。 彼はどのように働いていますか？

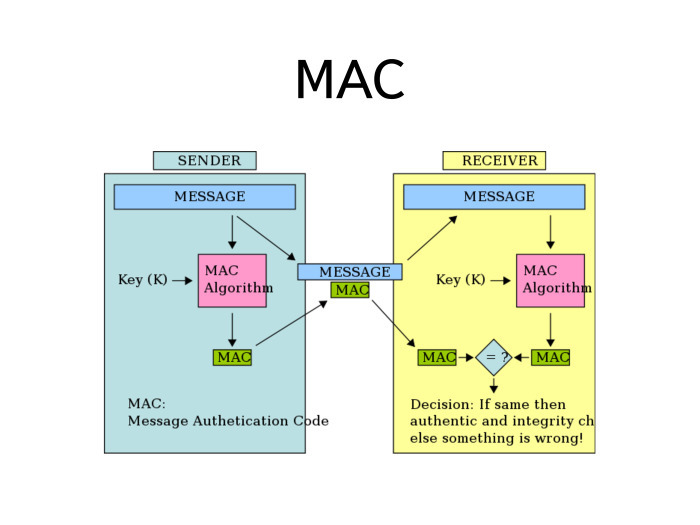
メッセージを受け取り、MACアルゴリズムと呼ばれる特別な機能を通過させます。 入力では、MACアルゴリズムはメッセージだけでなく、暗号化キーとは異なるキーも受信します。

メッセージを伝えたいときは、アルゴリズムの結果をそれに添付します。 受信者はメッセージを受け取り、同じ操作を実行して、計算したMACと受信したMACを比較します。 それらが一致する場合、プロセスでメッセージが変更されなかったことを意味します。 2つのMASが一致しなかった場合、途中で問題が発生しました。

MAC関数として使用できるものは何ですか？ ユニットの数を使用できますが、そのようなスキームは簡単に偽造されるようです。

ハッシュ関数は明らかな答えです。 そしてまた？

長い間、SHS MASが配布されていました。 初期化ベクトルがなく、他のすべてが同じである構造を取ります。 暗号化テキスト、暗号化、「チェーン」、暗号化、「チェーン」を取得します。最後のブロックが取得され、テキストに関するすべての情報が蓄積されます。 とても快適です。

しかし、MACの要素として何らかの暗号化ハッシュを使用できることも事実です。 いくつかの暗号化ハッシュがありますが、その中で最も一般的なものはMD5、SHAファミリ、GOST 34.11です...最近、SHA-3の競合が集まり、Keccakアルゴリズムが勝利しました。

ハッシュは暗号化アルゴリズムよりも複雑ですが、原則として、ハッシュ関数を構築するという考え方はブロック暗号化アルゴリズムに似ています。 つまり、いくつかのデータブロックを取得し、連続して、かなり基本的な操作のセットを数回適用します。 MD5を見ると、モジュロ2と巡回シフトだけが加算されています。 原則として、ブロック暗号化アルゴリズムの場合よりもはるかに多く適用します。 途中で1ブロックよりも長い関数を取得する必要があるテキストがある場合は、SHSに少し似た方法を使用してそれらを編集します。 これらのフラグメントを計算関数に追加します。

ハッシュの計算結果は数値です。 数値の長さは常に固定されています。 MD5の一般的なハッシュ出力サイズは、128ビット、SHA-1-168ビット、SHA-256-256ビット、SHA-384-384ビット、SHA-512-512ビットです。

ハッシュについて他に何が言えますか？ 入力に小さな変更がある場合、ハッシュは出力に大きな変更を提供する必要があります。 したがって、入力で平文の1ビットを変更した場合、理想的にはハッシュ（ハッシュ関数の計算結果）が正確に半分に変更されるはずです。

現在、実際には、SHA-2、具体的にはSHA-256またはSHA-384を使用することをお勧めします（ニーズに応じて）。 MD4は長い間壊れていました。MD5-原則としても壊れています。昨日、MD5に対する新しい攻撃が公開されました。 MD5の使用はもはや必要ないと想定できます。 実際には、常にSHA-2を使用してください。

認証に加えて、ハッシュ関数が使用される他の場所はどこですか？ PBKDF2などの鍵生成プロトコル。 ファイルを暗号化する必要があるとします。 ユーザーを取得し、原則として、ファイルの暗号化に必要なパスワードを要求します。 実際の状況では、ユーザーは1〜5のシーケンスのようなものをパスワードとして入力し、作業が完了します。

一方では、暗号化キーを「12345」ほど予測可能ではなく、ビット分布をより均一にする必要があります。 一方、攻撃者がすべての可能なパスワードオプションを整理し始めた場合、各ブルートフォース攻撃は可能な限り多くの時間を要するはずです。 示されたKDF関数のクラスは、これを正確に目指しています。

PBKDF2は、キー生成関数クラスの特定の関数です。 とてもシンプルに配置されています。 彼女は何万回もハッシュアルゴリズムを使用しているだけです。 そして、偶然-各段階で、追加のデータを混合するため、事前に計算するのはかなり困難でした。

ハッシュ関数はかなり長い間実行されているため、ハッシュ関数の実行には数千回も時間がかかります。 つまり、一般的なパスワードをいくつか試そうとする攻撃者から便利に保護されています。

実際には、KDF関数を使用する場合は、反復の数を選択することをお勧めします。これにより、一方ではせっかちなユーザーには受け入れられ、他方では数百万のキーを取得したい攻撃者には受け入れられません。 実際には、KDFで非常に多くの反復を選択して、たとえば1秒間実行します。 攻撃者にとって、1秒は絶対にわいせつな時間ですが、ユーザーはボタンを押してパスワードの確認を待つことで、1秒待つことができます。

パスワードの保存は、ハッシュの使用と同じです。 UNIXの話のアントンは確かにこれについて語っています。

オラクルのパディング攻撃と同様の攻撃があるため、メッセージを生成するとき、2つのオプションがあります。

MACのような暗号プリミティブがあり、暗号化のための暗号プリミティブがあります。 メッセージを送信して認証する必要があります。 2つの方法があります。 メッセージを暗号化してから、このモノからMACを取得してメッセージに添付できます。 完全に次のようになります：E（T）|| MAC（E（T））。

2番目の方法は次のとおりです。メッセージを取得し、暗号化して、クリアテキストからMACを取得します。 なぜ追加の操作が必要なのですか？

実際、1つは暗号化前のMACと呼ばれ、2つ目はMAC前の暗号化です。

質問-どちらが良いですか？ 同じですか？ OK、他のバージョンですか？

別の素晴らしい方法があります-彼らは言う、平文についての知識が流出しないようにMACを暗号化しましょう。

実際、この方法には問題があります。それを使用してメッセージを暗号化すると、パディングオラクル攻撃にさらされるリスクが発生します。 パディングオラクルは、MACが最後にあるか他のデータがあるかを心配しません。 最初にメッセージの復号化を試みるボックスがあります。 パディングが正しくないために復号化されない場合、MACボックスでもチェックされませんが、攻撃者または「このものを復号化できませんでした」とすぐに応答します。 不快なほどです。 したがって、このようなシステムの設計に関する一般的な推奨事項を次に示します。自分が何をしているのかわからない場合は、そのようなものを使用することをお勧めします。知っている場合は、これ：E（T）|| MAC（E（T））。

わずか6か月前、アントンと私は1つの場所について話し合い、2番目のデザインの使用を主張しました。 自分が何をしているのか知っていると思った。 そして、まだパディングオラクルがなかったので、私は自分が何をしていたかを知っていたようです。

メッセージを暗号化し、受信したメッセージが実際に送信者から来たことを確認できます。 : A B , .

, , , , , . - KDF- : , . .

? — . — . — . 100 , . , 100 , — .

, , , .

— .

?

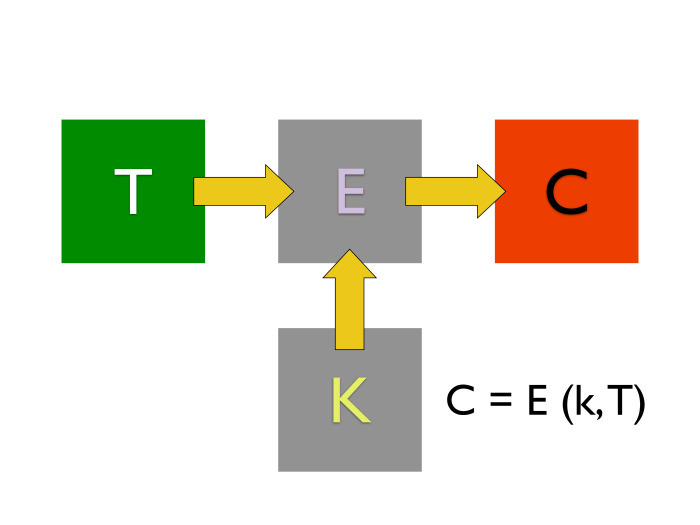
k ₁ k ₂ , . k ₁ , k ₂ . , .

: k ₁ k ₂ , , , . , .

, , . , , - .

, , , , P = NP. . RSA, , . .

, , . - (DH). , , .

. P G. .

a . .

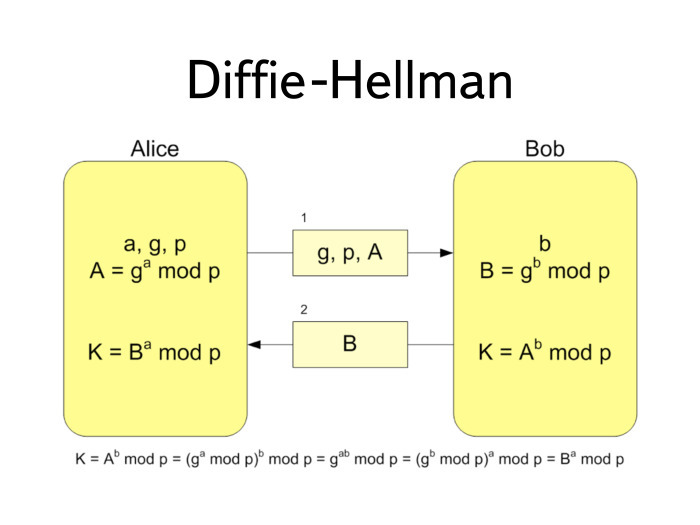
- , B . G P . , G P . .

? . , , , b. : ^a = A ^b . .

, , , . .

, , , , — 0.

, , — RSA.

. — 1024 . 2048, 4096 8192: , .

— .

(n-1)(p-1). — , .

, : , . - . .

— . , .

, d — . . , , . RSA.

, , . , k, , k — .


, - , - , n. . , , .

-, d.

de = 1 n, , M ^ed mod n, , M ¹ n. . M ¹ = M.

RSA, ? , k ₁ k ₂ , , — . — , d — . , , , , , . : M ^e , d, M ^d , .

RSA, ?

, - . XOR , . , , . . — , , .

. , , . RSA , — . . : - , - , , -.

RSA 1024, 2048, 4096 — . AES, DES Salsa : 256, 128 64 DES.

, — RSA-2048 AES-256? RSA , , AES 2 ²⁵⁶ , RSA — . , . 2 ²⁰⁴⁸ .

, , - - . , . , , . , .

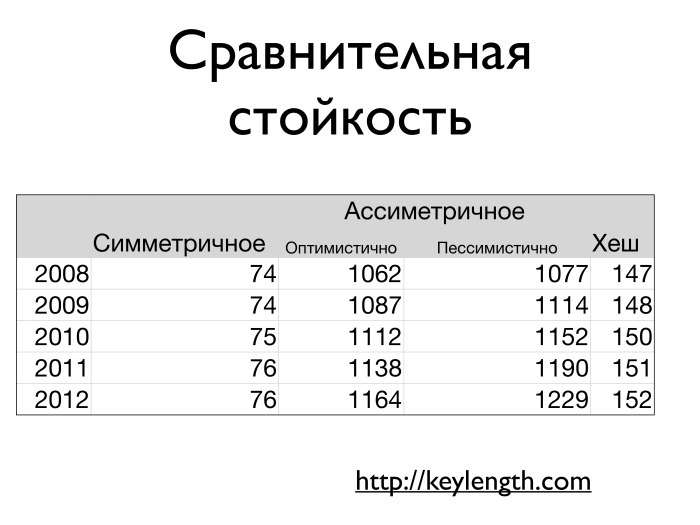
- , . , 2014 AES 78-80 . , RSA, 1300-1400 . keylength.com , . — 160-170 . SHA1 2014 , — 168 .

- , , .

. , , , .

. : . : . , .

. , email. , ?

— , 128 . ? , . .

, .

, , , .

.

. . , , - . , .

.

128- , . 128- , , . , . . .

? , . , . , , … - ?

, . . ?

, , … , . padding oracle, , , .

? , , , . , . , , — , .

, , . : , , . -, — . -, , .

? , , .

. , , S/MIME PGP. , , , .

, . , . , , . , . ? ?

: , DH , , . .

, DH, , , .

DH (. man-in-the-middle MITM — . .). , , , . , , - , , , , - . DH- — . , , .

どうする , .

— , — …

— ? ?

— …

-なんで？ .

— , .

— . , ?

— … .

— ? , DH : , , .

— DH- MITM?

-いいえ。 , DH-? , DH- . MITM , ? 信じられません

, ? . , A . それだけです .

? , . , . — , -, , , -, , .

: , , , . . DH.

, . , -. , , .

, . . - DH-, , ?

? , . . ? . - ? , . .

, - . . . : , , , , — . あまり便利ではありません。 , , MD5 SHA, . , - . HMAC. , .

, , . , , . C ₁ . , C ₂ , , .

. , . DH, DH . , - KDF-, : . , . — : , . — KDF-.

, , , , .

, , . , . , . HTTPS , , .

. . , . . , . , . — .

, ?